More than 3 years have passed since last update.

High Power Gear Boxを用いたDCサーボの制御設計 - 外乱オブザーバ

Posted at 2020-07-19

制御系の設計へ

上の記事の続きとなります。
前回では, パラメータを獲得し, ハンドチューニングによるPD制御にて位置制御を行いました。
今回は得たパラメータの妥当性の検証や, 数式に基づいた制御系設計を行いたいと思います。また外乱が発生したときにどのようにして外乱を補償するかについて書いてみたいと思います。

パラメータ取得と検証

前回得たパラメータの検証を行うため, 得たモデルと実際の装置に同じ制御をかけて比較をしてみます。
いかにSimulink モデルを示します。

また, 前回の手法でパラメータを取得しておきます。

$ K=482.58 $

$ T = 0.663 $


function J = myfunc(x,y,t,ts,Kp_id);

% Set identified parameters

K = 482.58
T = 0.663

% Discrete-time plant model
P  = K/(T*s^2 + s);
Pd = c2d(P,ts,'zoh');
[numpd,denpd] = tfdata(Pd,'v');

% Start experiment
tfinal = 16;
Kp     = Kp_id;
Ki     = 0;
Kd     = 0;
open_system('pos_pid_mbd_sl')
open_system('pos_pid_mbd_sl/Scope')
sim('pos_pid_mbd_sl')

% Save Parameters
save model_data K T numpd denpd

下図に比較結果を示します。傾向は一致しているかと思います。

極配置設計

ここではPDゲインの設計を極配置によって求めてみます。

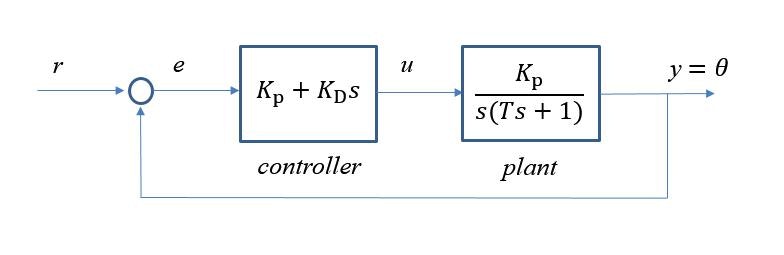
上図のフィードバックループにおいて, プラントの伝達関数 $P(s)$ を

$$ P(s) = \frac{K}{s(Ts+1)} $$

PD制御器の伝達関数 [tex:C(s)]を

$$
C(s) = K_{P} + K_{D} s
$$

と置きます。このフィードバックループの一巡伝達関数は

$$
G(s) = \frac{C(s)P(s)}{1+C(s)P(s)}
$$

$$
=\frac{(K_{P}+K_{D}s)\frac{K}{s(Ts+1)}}{1+(K_{P}+K_{D}s)\frac{K}{s(Ts+1)}}
$$

$$
= \frac{\frac{KK_{D}}{T}s+\frac{KK_{P}}{T}}{s^2+\frac{KK_{D}+1}{T}s+\frac{KK_{P}}{T}}
$$

伝達関数 $G(s)$ の極を$p_1$, $p_2$ とすると
$$
(s-p_1)(s-p_2) = s^2 -(p_1+p_2)s + p_1p_2 = 0
$$

上2式の係数を比較して,
$$
p_1 + p_2 = - \frac{KK_{D}+1}{T}, p_1p_2 = \frac{KK_P}{T}
$$

これらの式を$K_P$ , $K_D$ について解きます。
$$
K_P = \frac{p_1p_2 T}{K}, K_D = - \frac{(p_1+p_2)T+1}{K}
$$
と求めることができます。

今回では, 2次遅れシステムの伝達関数

$$
\frac{\omega_n^2}{s^2+2\zeta\omega_n+\omega_n^2}
$$

の極に等しくなるように$p_1$ と $p_2$ を設定します。上の伝達関数の分母式 ,
$$
s^2+2\zeta\omega_n+\omega_n^2 = 0
$$
の解は ,

$$
p_1 = -\zeta \omega_n + j\omega_n\sqrt{1-\zeta^2}
$$

$$
p_1 = -\zeta \omega_n - j\omega_n\sqrt{1-\zeta^2}
$$

と求められます。$\omega_n$ が大きいほど, 収束が早くなります。 $\zeta = 1$ のときに臨界減衰応答となります。

$\omega_n$ と $\zeta$ を与えて極配置を行ってみます。

例えば

$\omega_n = 10$

$\zeta=0.65$

% pos_pd_mbd.m

% Initialize & load data
close all
clear all
load sim_param
load model_data

% PD design by pole placement
omega_n = 10;
zeta    = 0.65;
p1 = (-zeta + j*sqrt(1-zeta^2))*omega_n;
p2 = (-zeta - j*sqrt(1-zeta^2))*omega_n;

% Set PD parameters
Kp = p1*p2*T/K;
Kd = -((p1+p2)*T + 1)/K;
Ki = 0;

% Experiment
r      = 60;
r_cyc  = 4;
dist = 0;
Ncyc   = 4;
tfinal = r_cyc*Ncyc;
open_system('pos_pid_mbd_sl')
open_system('pos_pid_mbd_sl/Scope')
sim('pos_pid_mbd_sl')

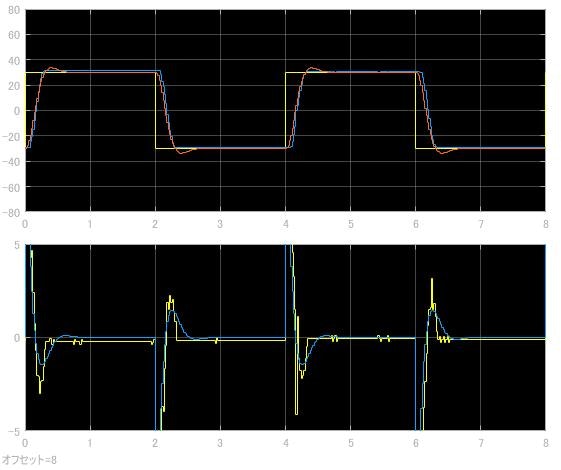
にて実行すると

おおむね応答が一致していると思います。ギア部分の摩擦が要因でしょうか, オーバーシュートは少し抑えられています。

この時のゲインは

$ K_p = 0.1371 $

$ K_d = 0.0131 $

となりました。

外乱

前回の位置制御系では, 制御プラントが積分器を有しているため, I制御なくとも指令に追従しました。
しかし外乱に対しては有効ではなく, 偏差を生じます。

"外乱 - 通信系などに外から加わる不要な信号。雑音あるいは妨害ともいう。"

今回は制御系におけるものですね。
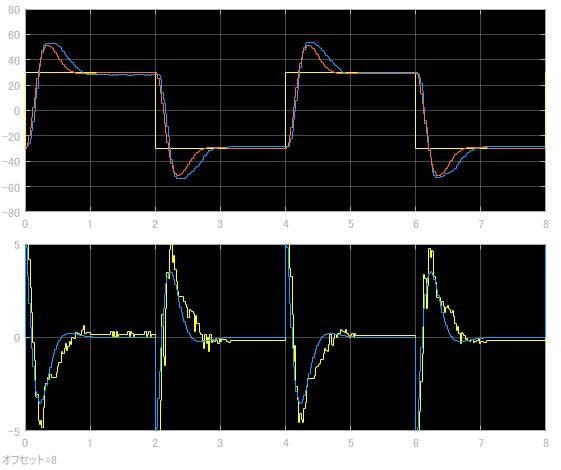
以下の図に制御入力に定常的な外乱（電圧オフセット）を加えた時の応答を示します。

このように, 偏差を確認することができます。

外乱オブザーバ

外乱オブザーバは, フィードバックループ内に外乱が発生する状況で, 外乱を推定して制御入力にフィードバックをかけることで, 比較的に簡易に外乱を除去し安定化することができます。補償器のひとつです。

外乱オブザーバとは
http://arduinopid.web.fc2.com/O23.html
外乱オブザーバの紹介
https://qiita.com/wcrvt/items/073d0256ccdac423c2fe

今回は作ったサーボ系で動作を確かめてみようと思います。

外乱オブザーバの原理

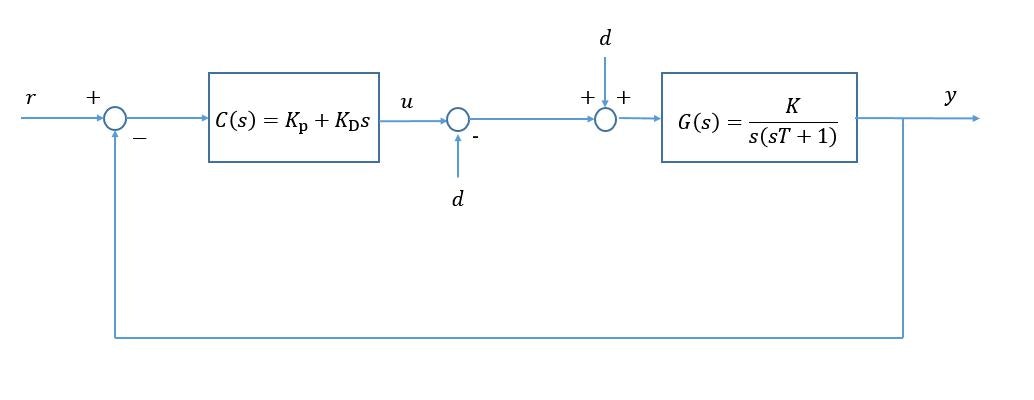
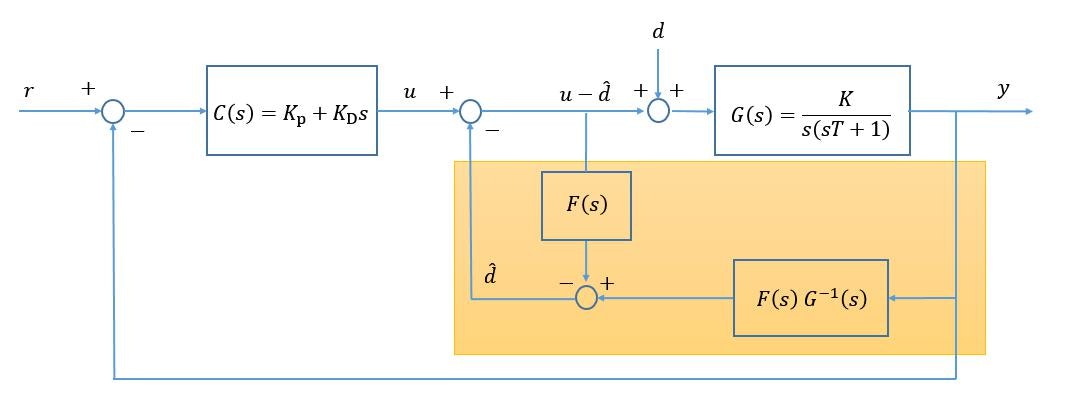
今回の制御ループで外乱を有するときのブロック図を以下に示します

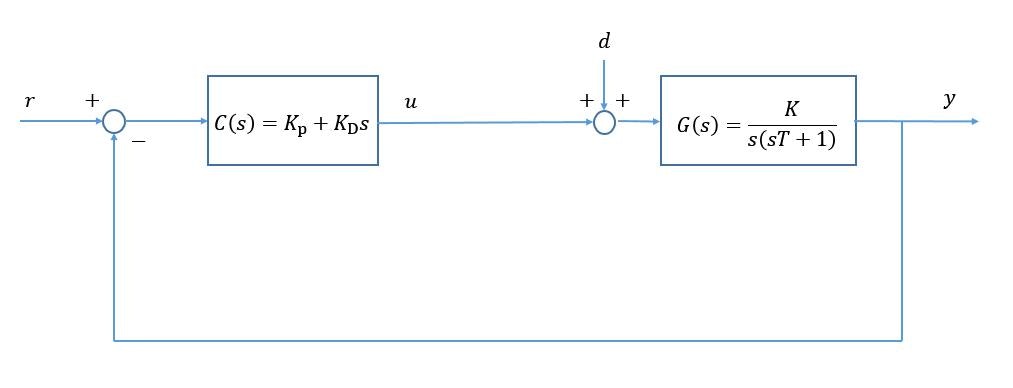
このときの出力 $y$ は,

$$
y = (u+d) G(s)
$$

となります。コントローラによって制御された入力が外乱によって変化してしまいます。

上の例では, $d$ に一定値を入力しているので, オフセットの電圧がモータドライバに印加され, 定常偏差が発生します。

コントローラ側から生成される制御量から外乱を推定して, 制御入力に外乱 $d$ を差し引いておくことで外乱の影響を除去することができます。

この場合の出力 $y$ は,

$$
y = (u+d-d) G(s)
$$

$$
= u G(s)
$$

となり, 適切に制御されます。(外乱があらかじめわかっているのなら, フィードフォワードで差し引けば外乱を除去できます。)

本質はどう外乱を推定するかにあります。

出力は外乱を受けた後の出力となるため, ここから推定することができそうです。出力 $y$ の式は,

$$
y = (u+d) G(s)
$$

ここで制御プラント $G(s)$ が逆システム $G(s)^{-1}$ が存在すれば,

( 今回は$G(s)^{-1} = {s(sT+1)}/{T}$となります )

$$
y G(s)^{-1} = u+d
$$

$$
\hat{d} = y G(s)^{-1} - u
$$

となり, 推定外乱 $\hat{d}$ を求めることができます。

ブロック図で表すと以下のように表現することができます。

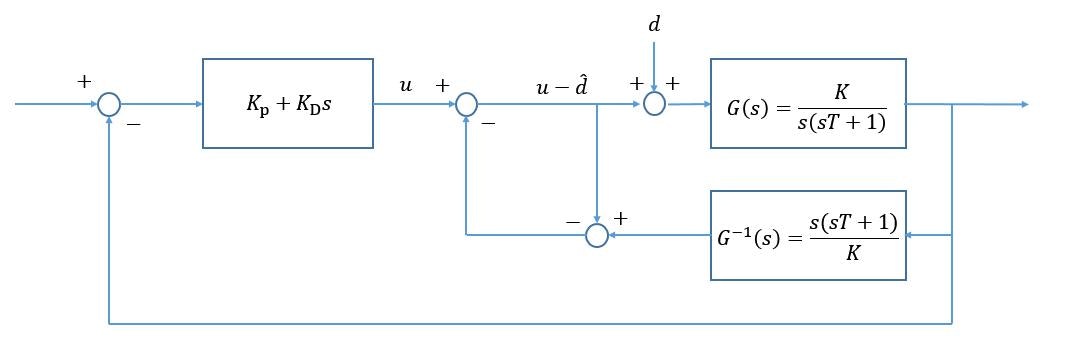
オレンジ部分がオブザーバの表現になります。
コントローラによって生成される制御入力は, 推定外乱と外乱を受けて$u-\hat{d}+d$ となるので,
出力 $y$ は,
$$
y = (u-\hat{d}+d) G(s)
$$

となり, 推定外乱 $\hat{d}$ は,
$$
\hat{d} = y G(s)^{-1} - (u - \hat{d})
$$

$$
= (u-\hat{d}+d) G(s) G(s)^{-1} - (u - \hat{d})
$$

ここで $G(s)$ とその逆システム $G(s)^{-1}$ の積 $G(s)G(s)^{-1} = 1$ とすると,

$$
\hat{d} = d
$$

が成立します。このような原理で外乱を除去します。

プログラム上で制御対象の伝達関数 $ G(s) $ , またその逆関数 $ G(s)^{-1} $ を利用して制御する方式をモデル規範型制御とも呼んだりするそうです。

外乱オブザーバの実用上の運用

今回の制御プラントは逆システム $ G(s)^{-1} $ が得られます。運用上で注意すべきことがあり, フィルタの設計になります。逆システムの式、$ G(s)^{-1} $　には微分項が含まれています。

微分動作は基本的に不安定な要素のため, これを避けるためにプロパーな関数にします。具体的な操作としては分子多項式の次数が分母多項式の次数以下にするためローパスフィルタを使います。

今回私は, Butterworthフィルタを選定しました。

$$
F(s) = \frac{\omega_c^2}{s^2+\sqrt{2}\omega_c s + \omega_c^2}
$$

カットオフ周波数 $ \omega_c $ となります。

推定外乱にフィルタをかけることも多いそうですが, ループ内に微分器が残ってしまうパスが残ってしまうので, ローパスフィルタを分散して次のように設定します。

こうすることで出力項は以下のように変形され, プロパーな項となります。

$$
F(s) G(s)^{-1} = \frac{\omega_c^2}{s^2+\sqrt{2}\omega_c s + \omega_c^2} ・ \frac{s(sT+1)}{T}
$$

$$
= \frac{\omega_c^2 \tau s^2 + \omega_c^2 s}{s^2+\sqrt{2}\omega_c s + \omega_c^2}
$$

このように分母次数と分子の次数が等しくなり, $F(s)G(s)^{-1}$ は (なんとか) 動作します。

MATLAB/Simulinkでシミュレーション・実行する際に, 逆システム（を離散化したもの）をそのままの伝達関数として扱うことはできません。(プロパーでない（非因果モデルに使用できません）とでます)

よってこのような方法を取っています。

動作検証

あらかじめシステム同定を行い, パラメータを取得しておきます。

$K = 570.860$

$ T = 0.5311$

ゲインの計算とオブザーバ（とフィルタ）の設定と実行します。

% pos_pd_mbd.m
s = tf('s');

% Initialize & load data
close all
clear all
load sim_param
load model_data

% PD design by pole placement
omega_n = 10;
zeta    = 0.65;
p1 = (-zeta + j*sqrt(1-zeta^2))*omega_n;
p2 = (-zeta - j*sqrt(1-zeta^2))*omega_n;

% Set PD parameters
Kp = p1*p2*T/K;
Kd = -((p1+p2)*T + 1)/K;
Ki = 0;

% observer setting
omega_c = 7;        % cutoff frequency
Fs = omega_c^2 / (s^2 + sqrt(2)*omega_c*s+omega_c^2);
Fsd = c2d(Fs,ts,'zoh');
[numfsd,denfsd] = tfdata(Fsd,'v');  % discrete filter
invP = s*(T*s + 1)/K;   % inverse model
Est = Fs * invP         % estimation
Estd = c2d(Est,ts,'zoh');
[numestd,denestd]  =tfdata(Estd,'v'); % discrete model

% Experiment
r      = 60;
r_cyc  = 4;
dist   = 2; % 0 or 2 for dist test
% dist = 0;
Ncyc   = 4;
tfinal = r_cyc*Ncyc;
open_system('pos_pid_mbd_sl_observer')
open_system('pos_pid_mbd_sl_observer/Scope')
sim('pos_pid_mbd_sl_observer')