本記事では外乱オブザーバを用いた2自由度制御について紹介します。
Matlab/Simulink Advent Calender 2019にて同日公開予定の記事とペアとなっています。こちらにて2自由度制御系の説明とフィードフォワード制御の紹介しています。
Matlabにおける状態空間表現を用いた2自由度制御と完全追従制御の紹介
https://qiita.com/wcrvt/private/e198ad9ead4a8bf80af4
フィードフォワード制御は高速に動作させることを目的としていますが,フィードバック制御はあらゆる環境下での動作を保証するために使用されます。産業用ではフィードフォワード制御が強力な手法となっていますが,ヒューマノイド等,未環境下での一定の性能を保証するためには,フィードバック制御の技術が不可欠となります。
はじめに
外乱オブザーバは慶應義塾大学名誉教授/KGRI特任教授の大西公平先生が発明されました。初めて公の学会に発表されたのは,1983年に東京で開催された,日本の電気学会が主催するパワーエレクトロニクス国際会議であるIPECです。
Kiyoshi Ohishi, Kouhei Ohnishi, and Kunio Miyachi,"Torque-speed regulation of dc motor based on load torque estimation method," JIEE/1983 International Power Electronics Conference, IPEC-TOKYO, Tokyo, Japan, 27th Mar - 31st Mar.
大西研究室のホームページで,IPECの冊子写真(緑色)をクリックすると読むことができます。
http://www.sum.sd.keio.ac.jp/
第一著者は長岡技術科学大学教授の大石潔先生です。大石先生が学生であった際の研究が外乱オブザーバであり,修士論文および博士論文は慶應義塾大学矢上キャンパスの図書館に保管されています(学士論文は保管なし,修士論文は複写禁止)。
外乱オブザーバの成果が認められてから長い時間が経ちましたが,さらに優れた制御系が現れることを期待しています。そこで,温故知新ということで外乱オブザーバの構造を確認していこうと思います。
外乱オブザーバについて
外乱オブザーバの構成方法は,電気系(モータドライブ技術等)の発展や外乱オブザーバの伴って変化しており,現在では次のように構成されます。
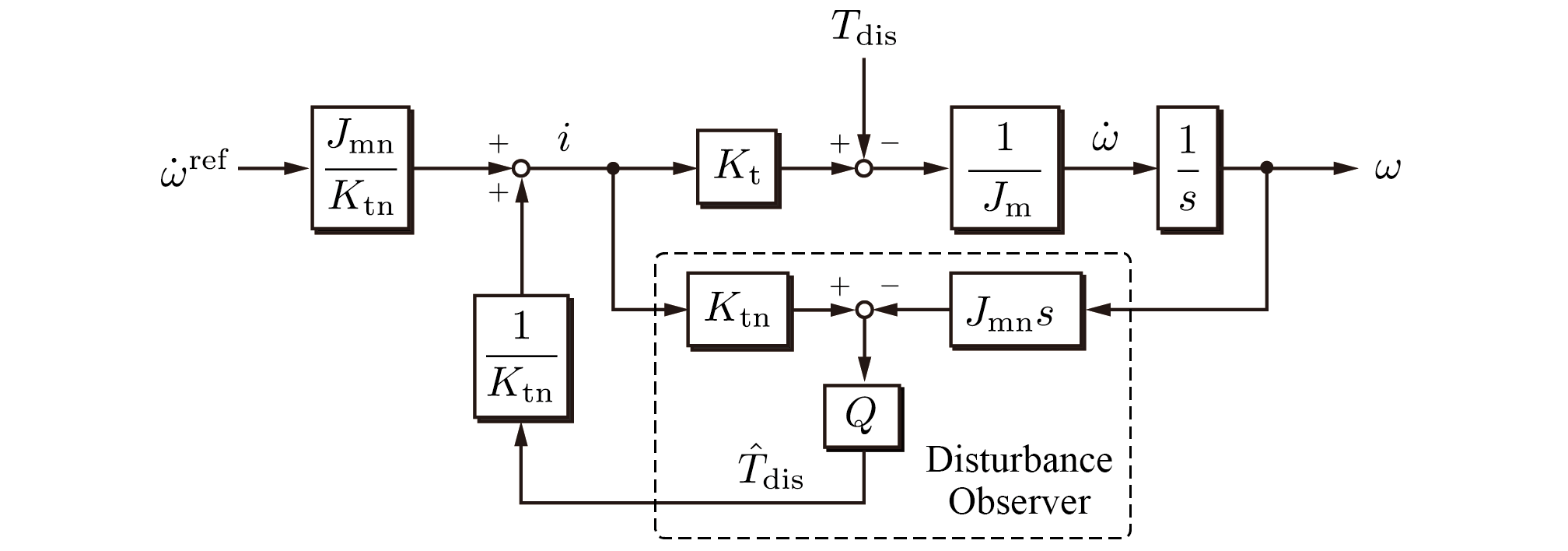
$\omega$はモータ回転速度,$J_{\rm m}$はモータ慣性,$K_{\rm t}$はトルク定数,$T_{\rm dis}$は外乱,$i$は電流,$Q$はフリーパラメータです。オブザーバということで元々は外乱自体を推定する機構ですが,推定した外乱をフィードバックすることでロバストな制御系を構築するために使用します。外乱オブザーバの大きな貢献は,加速度次元における制御を可能としたことです。上のブロック線図で,外乱がない場合に,加速度参照値$\dot{\omega}^{\rm ref}$と加速度応答値$\dot{\omega}$が一致します。昔の技術者は「運動制御における問題は加速度の制御によって単純なものとなる」と知っており,外乱オブザーバを用いた制御は所望の加速度を制御するために非常に便利なものでした。
外乱オブザーバの導出
上で紹介した下記の論文を見てみます。
Kiyoshi Ohishi, Kouhei Ohnishi, and Kunio Miyachi,"Torque-speed regulation of dc motor based on load torque estimation method," JIEE/1983 International Power Electronics Conference, IPEC-TOKYO, Tokyo, Japan, 27th Mar - 31st Mar.
この論文を読んでも,外乱オブザーバの導出方法については詳細な記載はされていません。技術漏洩を防ぐために,導出方法を記載しなかった可能性があります。上記論文では,外乱オブザーバの導出に際してに2件の論文を引用しています。B.Gopinathの最小次元オブザーバの構成方法に関する論文と,J.S.MeditchによるUnknown Input Observer(UIO)です。UIOから着想を得て,導出にはGopinathの方法を使用して導出が可能です(Gopinathの方法: https://github.com/wcrvt/Textbook/blob/master/Gopinath.pdf )。実際に,初期の論文ではGopinathの方法に基づいた最小次元オブザーバの形式で外乱オブザーバが構成されています。Gopinathの方法を用いているということで,外乱オブザーバは必然的にLuenbergerのオブザーバの一種であり,状態空間表現を用いて導出されています。当時はモータ制御に電流制御が使用されておらず,電圧制御を含めた状態空間が記載されています。ここでは簡単に,電流制御系を用いたモータ制御系(出力トルクが制御しやすい表面永久磁石型同期モータを使用しているものとします)における外乱オブザーバを導出してみます。
次のシステムの外乱を推定することを考えます。観測可能状態量はモータ電機子電流およびモータ回転速度とします。
\dot{\omega}=\frac{1}{J_{\rm m}}T_{\rm dis}+\frac{K_{\rm t}}{J_{\rm m}}i
モータの発生トルクは$K_{\rm t}i$となります。初期の外乱オブザーバは,一定外乱の抑圧を目的に開発されました。そのため,定常外乱の観測に焦点を当てています。そこで,$\dot{T}_{\rm dis}=0$と仮定を置いて,状態空間表現を構築します。
\begin{align}
\frac{d}{dt}
\begin{bmatrix}
T_{\rm dis}\\\omega
\end{bmatrix}&=
\begin{bmatrix}
0 & 0 \\ \frac{1}{J_{\rm m}} & 0
\end{bmatrix}
\begin{bmatrix}
T_{\rm dis}\\\omega
\end{bmatrix}+
\begin{bmatrix}
0\\\frac{K_{\rm t}}{J_{\rm m}}
\end{bmatrix}i\\
y&=\begin{bmatrix}
0 & 1
\end{bmatrix}
\begin{bmatrix}
T_{\rm dis}\\\omega
\end{bmatrix}
\end{align}
このように拡張したとしても,可観測性が確保されています(可観測行列が正則)。あとはGopinathの方法を使用します。ここでは結果だけ記載しますが,このオブザーバの推定は少し不思議な形となります。
\hat{T}_{\rm dis}=-\frac{L}{s+L}(K_{\rm t}i-J_{\rm m}s\omega)
ここで,$L$はオブザーバゲインです。実は,現在一般化されている外乱オブザーバは,システムに印加される外乱と逆相の信号を推定しています。外乱オブザーバのブロック線図では,負極性の外乱を入力して正極性の外乱を推定しています。そのため,上式に出てきた負符号は取り払われています。この式だけ見ると,出しているだろうトルク($\tau=K_{\rm t}i$)から入ってきていたトルク($\tau=J_{\rm m}\dot{\omega}$)を差し引いて,低域通過フィルタに通して推定しているだけに見えます。
外乱オブザーバと2自由度制御系の関係
外乱オブザーバの着想の一つですが,長岡技術科学大学 大石先生は1自由度制御系に見られる極零配置問題(https://qiita.com/wcrvt/private/e198ad9ead4a8bf80af4 にて簡単に紹介)を解決するために外乱オブザーバが効果的であることに言及しています。
大石 潔, 大西 公平, 宮地 邦夫,「状態観測器を用いた他励直流機の一制御法」,電気学会論文誌B, 104巻, 6号 p. 373-379, 1984.
外乱抑圧に設計自由度を持たせることは,2自由度制御と同じ発想です。これに対して,Youla-Kuceraによって定式化された2自由度制御系の一般系から外乱オブザーバを導出し,外乱オブザーバが2自由度制御系に属することを示した方々がいらっしゃいます。
松本 和則, 鈴木 達也, S. Sangwongwanich, 大熊 繁, 「2自由度制御系の内部構造と補償器のフリーパラメータの一設計法」, 電気学会論文誌D, 113巻, 6号 p. 768-777, 1993
2自由度制制御系の一般系を少し変形するだけで,外乱オブザーバと同様になることが確認できます。そして,外乱オブザーバは加速度次元における2自由度制御系だということが分かります。簡潔に纏めた資料を以下に置いておきます。
数式を追うのが面倒な場合,簡単なブロック線図の変形からも上記事項を確認することができます。
https://github.com/wcrvt/Textbook/blob/master/Structure_DOB.pdf
H-infinity制御との比較
当時千葉大学に所属されていた美多勉先生が,1995年に外乱オブザーバと$H_{\infty}$制御の比較をしておられました。
美多 勉, 平田 光男, 村田 健一,「$H_{\infty}$制御と外乱オブザーバの理論」,電気学会論文誌C, 115巻, 8号 p. 1002-1011,1995
この論文では,外乱オブザーバが単なる1型サーボで,大した制御系でないと仰っている。これに対し,大西先生は当初の外乱オブザーバはステップ外乱のみ着目して導出されたものであるから,1型サーボになるのは当然だと仰っていた記憶がある。実際,外乱の特性を考慮した外乱オブザーバの設計例は報告されている。外乱オブザーバの利点は,外乱生成多項式をフリーパラメータに組み込むことで外乱の抑圧が可能である点であり,1993年に発表された2自由度制御系としての枠組みを見れば容易に理解できる。ただし,美多先生の仰ることは御尤もで,既知環境下の既知制約に対して制御器の最適化を行う$H_{\infty}$制御系には,正直勝つことは難しいと考える。
美多先生の綺麗な数式を用いた研究は,現在では千葉大学の劉康志先生の研究室に引き継がれていると思います。共著者の平田先生は,現在宇都宮大学でロバスト制御,PWMインバータの厳密線形化を含む精密制御,UAV(所謂ドローン)や自動車駆動部の制御,機械学習を用いた以上検知など様々な研究をされていたと記憶しています。現在でも自宅で実験を行なっていると伺った記憶があるのですが,非常に深い実学的な知見をお持ちだと存じています。平田先生の執筆された参考書を以下に紹介します。
https://www.coronasha.co.jp/np/isbn/9784339033113/
外乱オブザーバの実績と利点
外乱オブザーバは性能として$H_{\infty}$制御に勝つことは難しいかもしれません。それでも外乱オブザーバを使う意味はあるのかと言われると,正直な話どうでもいいと思います。コントローラプラットフォーム(計算機)の性能が決まってしまえば,どんな制御系を組んでも調整次第で大体同じ性能が出る,というのは制御設計者ならある程度の経験があるのではないでしょうか。利点の前に,外乱オブザーバの実績について振り返ります。
外乱オブザーバの素晴らしい点は,加速度制御系の実現と,アプリケーションの開拓にあったのかと思います。上で説明しましたが,外乱オブザーバを使用することで加速度次元の2自由度制御を構築可能です。精密位置決めのように,位置制御系に対して2自由度制御系を構築することとは意味が異なります。実際,振動制御ではエネルギの流れ,駆動側と負荷側のインピーダンスマッチングを取るために慣性制御の需要がありましたが,加速度制御を通じて慣性制御を行うことで,振動制御が実現されました。他にも,力制御やコンプライアンス制御のような接触タスクを含むシステムの制御系構築にも,非常に効果的でした。私の意見ですが,この加速度制御の汎用性の実証が強かったと思います。
参考文献:
K. Ohnishi, M. Shibata and T. Murakami, "Motion control for advanced mechatronics," in IEEE/ASME Transactions on Mechatronics, vol. 1, no. 1, pp. 56-67, March 1996.
また,加速度制御系は多軸ロボット制御も簡単にします。京都大学名誉教授の吉川恒夫先生は,1980年代にロボットに任意の動作をさせるために必要な関節モータのトルクを与えています。
・下記論文(22)~(25)式
吉川 恒夫, ロボットアームの位置と力の動的ハイブリッド制御, 日本ロボット学会誌, 3巻, 6号, p. 531-537, 1985.
・(25)式は下記論文内にて訂正されています。
吉川 恒夫, 杉江 俊治, 田中 正樹, ロボットアームの位置と力の動的ハイブリッド制御, 日本ロボット学会誌, 6巻, 5号, p. 380-387,1988.
参考文献には,Boston DynamicsのM.H.Raibertが位置と力のハイブリッド制御を行なっていた論文が記載されています。彼のホッピングの研究等も面白いので,興味がある方は読んでみてください。
上記論文では出力されるべき加速度が(25)式に記載されており,この加速度の再現を外乱オブザーバを用いた加速度制御系で行い,多自由度制御を行う方法が下記に記されています。
村上 俊之, 大西 公平, ロバスト制御に基づいた多自由度ロボットの安定性および作業空間での非干渉制御に関する一考察, 電気学会論文誌D, 113巻, 5号, p. 639-646, 1993.
著者の慶應義塾大学 村上先生は,多自由度制御に関する研究で博士論文を執筆されているため,非常に参考になります。正直な話,吉川先生の論文は非常に難しいので,こちらの方が読みやすいと思います。
ロボットで加速度制御が実現できると何が良いかというと,ロボットのインピーダンス,物体との接触時および衝突時のインピーダンスを自由に設定可能であるという点です。ロボットが持つべきインピーダンスが設定されれば,接触が生じた際にロボットがすべき運動というのが決定されます。その運動の加速度を生成することで,所望の運動を実現します。このように,外乱オブザーバを用いた加速度制御は非常に使い勝手が良かったという背景があります。
これを踏まえた上で,加速度制御系を構築できればどんな制御系でも良いと考えています。それは,上に示した線形制御器でなく,スライディングモード制御でも構いません。ただ,加速度制御系を構築する上で,私は外乱オブザーバを用いた形式が楽なので使っています。また,未知環境下ではなにが起こるのかわからないので,$H{\infty}$制御のようにゲインを上げられる所は上げておく,といった方式があまり意味を為さないと考えています。加えて,基本的に加速度制御系はカスケード制御系の方式で採用されるので,上位(外側)の制御系に「どの帯域まで制御可能か」を伝える必要があります。その際,内側の加速度制御系の特性はシンプルであって欲しいですし,単純な外乱オブザーバを使用すれば加速度制御帯域が簡単に設定できます。ゲインが上がらなければ,ロボットの機構,電力系(ドライブシステム),計算機を見直せば良い話だと思います。ただ,人それぞれ設計思想がありますし,無理に外乱オブザーバを無理に使う必要はないし,個人の判断に委ねたいと思います。
2000年以降の研究
大西先生の研究室は,2000年代の頭からハプティクス(力触学)の研究を始め,先生はこの功績から2016年に紫綬褒章を受賞されています。慶應義塾大学のハプティクス技術は加速度制御技術に基づく位置と力の4chバイラテラル制御(位置と力の情報を2つのシステム間で受信・送信するために4本の経路が必要)という制御を核としており,高い性能を示しました。このころから外乱オブザーバの研究自体は減り,応用する方面に移行したと思います。
そのような中で,外乱オブザーバのモデル化誤差が制御に与える影響を,振動制御の安定化のために使用した研究が発表されました。
桂 誠一郎, 大西 公平, 位相進み補償に基づく多慣性共振系の振動抑制制御, 電気学会論文誌D, 2006, 126巻, 12号, p. 1601-1607, 2006.
結論から述べると,外乱オブザーバのパラメータ設定によって制御ループ内に位相補償効果が入り,位相余裕改善が達成されるために振動抑制に効果的であった,ということを報告しています。外乱オブザーバのパラメータをどのように設定すれば良いかについて簡潔な解を与えています(設定する慣性値を大きくしておけば良い,というもの)。これ以降,この位相補償効果を使用して何かを達成しようとする動きが見られました。数年前にも外乱オブザーバのパラメータ設定により制御性能の向上を目指す研究が行われています。
E. Sariyildiz and K. Ohnishi, "Stability and Robustness of Disturbance-Observer-Based Motion Control Systems," in IEEE Transactions on Industrial Electronics, vol. 62, no. 1, pp. 414-422, Jan. 2015.
非常に多くの数式を用いて説明されており,次第に複雑化するような流れがありました。この流れに対して,私は疑問を持っています。名古屋大学 鈴木達也先生が20年前から仰るように外乱オブザーバは限定的な2自由度制御系であるため,このように複雑化して考えることは如何なものか,ということです。そもそも外乱オブザーバが単純さを欠くなら$H_{\infty}$制御の方が良いと思いますし,恣意的なパラメータ設定で制御器の調整を行うくらいなら制御ループに位相進み補償器を挿入する方が良いと考えています。
また,ハプティクスの性能を向上するために,外乱オブザーバの性能を向上しようとした研究がありました。FPGAを使用して制御系を実装したり,マルチレート系で外乱オブザーバを組んだりしています。
石井 恵奈, 桂 誠一郎, 西 宏章, 大西 公平, FPGAを用いた多自由度バイラテラル鉗子ロボットシステムの構築, 電気学会論文誌D, 127 巻, 5 号, p. 508-517, 2007.
水落 麻里子, 辻 俊明, 西 宏章, 大西 公平, マルチレートサンプリング手法を用いた加速度制御系の実現, 電気学会論文誌D, 126 巻, 3 号, p. 261-268, 2006.
共著に入られている慶應義塾大学 西宏章先生は計算機学を専門としており,実学的な面で大きな進展があったと思います。また,実現可能な最適な外乱オブザーバを実装するために,カルマンフィルタ型の外乱オブザーバが提案されています。私の知る限りでは,下記の学会で発表されたものが初めだと思います。
ヨーンヤィ チャイサモーン, 島田 明, 藤井 信之, カルマンフィルタ型外乱オブザーバと外乱推定値の利用に関する一考察, 自動制御連合講演会講演論文集, 第51回自動制御連合講演会, 51巻, 2008.
その後は芝浦工業大学 島田明先生の研究グループや長岡技術科学大学 大石潔先生の研究グループでカルマンフィルタ型の外乱オブザーバを使用した研究を見ます。私はこの研究を見る度に外乱とその分散の定義方法に疑問を覚えており,これらの設計には研究グループに蓄積された知見に依存するものが大きいと感じています。カルマンフィルタを含む現代制御の理念は,状態空間表現を与えることにより一意の解を得ることですが,フィルタパラメータの調整が大変なのであれば手動でフィルタを設計した方が良いと考えています。一般的な設計方法が確立された後に,再びこの研究を見たいと考えています。また,カルマンフィルタは可変ゲインオブザーバとなりますが,加速度制御の帯域がロボットの姿勢によって変化するといったことがあると非常に面倒なので,その辺について知りたいとも思います。カルマンフィルタの実用とは少し離れますが,雑音分散値から一意に求まる定常カルマンゲインを用いて実現可能な制御帯域を推定することも有効だと思います。
その他,長岡技術科学大学 大石潔先生の研究グループで摩擦フリー外乱オブザーバと言うものが提案されています。ディザを用いて摩擦の影響を低減し,なおかつ外乱推定のプロセスでディザの影響をきっちり除去する,といったものだと把握しています。このオブザーバにもカルマンフィルタが導入されています。ハプティクスに応用された研究がありましたが,装置を触ったことがないのでどれくらい凄いのか分からないのが残念です。
T. T. Phuong, K. Ohishi, Y. Yokokura and C. Mitsantisuk, "FPGA-Based High-Performance Force Control System With Friction-Free and Noise-Free Force Observation," in IEEE Transactions on Industrial Electronics, vol. 61, no. 2, pp. 994-1008, Feb. 2014.
Thao Tran Phuong, Kiyoshi Ohishi, Chowarit Mitsantisuk, Yuki Yokokura, Kouhei Ohnishi, Roberto Oboe, Asif Sabanovic, Disturbance Observer and Kalman Filter Based Motion Control Realization, IEEJ Journal of Industry Applications, vol. 7, no. 1, p. 1-14, 2018.
余談
通信分野で発明され,パルス密度変調などで使用されるデルタシグマ変調(シグマデルタ変調)は,少し変形すると外乱オブザーバと同じ形となります。デルタシグマ変調は当時早稲田大学に在籍した東京大学名誉教授/早稲田大学名誉教授の安田靖彦先生によって,1961年にデルタ変調を基に考案されています。用途が異なっても,2自由度制御系の構造に落ち着いたところは面白いですね。
最後に
モーションコントロールの性能は,制御アルゴリズム,演算器性能,モータドライブ性能,センサ性能など様々な要因によって決定されます。
S. D. Eppinger and W. P. Seering, "Three dynamic problems in robot force control," Proceedings, 1989 International Conference on Robotics and Automation, Scottsdale, AZ, vol. 1, pp. 392-397, 1989.
この記事の前半で紹介した論文は殆どが1990年代までに公開された論文です。この時点でロボット制御の理論体系の大枠は大体出来上がっているように感じていて,2000年以降は実用方面の研究がなされていると思います。もっと実学的に複合領域の研究をやっても良いのではないかと私は考えています。千葉工業大学教授の熱海武憲先生は,精密制御と振動制御に関する研究において,制御系設計と機構設計で協力することを提唱されています。
T. Atsumi, T. Shimizu, T. Arisaka, and H. Masuda, “Integrated design of a controller and a structure for head-positioning in hard disk drives,” Journal of Vibration and Control, vol. 12, no. 7, pp. 713–736, July 2006.
制御しやすい共振特性になるように機構設計をしたら制御性能が一気に上がった,とのことです。加えて,製品の質が一気に向上したので,会社内の制御設計班と機構設計班が互いに褒め合って仲が非常に良好になり,良いことだらけと仰っていました。
私はFPGAを用いて制御演算用チップを作成しています。汎用プロセッサにはないレスポンシブ,厳密一様サンプリング,高スループットなど様々な利点が得られます。これにより,広帯域の制御が実現できたりします。なぜ態々開発するかというと,汎用的なプロセッサが今後発展しても,なかなか制御性能の向上に繋がるとは考えていません。プロセッサのマイクロアーキテクチャはその時代の最も大きい需要に適うように設計されるので,制御設計向けのプロセッサというのは出てこないと思います。しかし,現状のロボットは制御があまり上手く行っていないので,制御用チップを作ることは大事かなと考えています。プロセッサ開発が得意でロボット制御に興味がある方,ロボットが制御が得意でチップ開発に興味がある方とか,いらっしゃらないでしょうか。