超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)⓪
超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)①
超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)②
超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)③ Rで作る回帰決定木
超初心者が学ぶランダムフォレスト・分類回帰樹木 ④ アンサンブル学習とは
もどうぞ
ランダムフォレストのアルゴリスムの勉強とRコードによる実装です。
分類・回帰の両方で実践してみます。
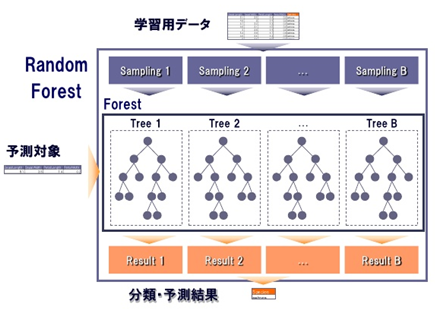
ランダムフォレストとは
決定木(CART樹木)をランダム性を注入して生成することに由来します。アンサンブル学習の中でも、精度の高いといわれている勾配ブースティング等を含むブースティング法(GBM)に匹敵する精度を得ることができます。
また、ブースティング法よりも計算速度が速く、外れ値やノイズに対しても頑健なのが特徴です。
概要
ランダム性とは何なのか?
それは一本一本の決定木を生成するときに導入される要素を指します。標本選択と変数選択によってランダム性が注入されます。
・標本選択
母集団からブートストラップ標本$\varphi^{(b)}$を生成します。
ブートストラップとは、n標本から構成される母集団から、重複を許してn個を選択する方法です。これで決定木毎に使用する標本(ブートストラップ標本)が異なるため、ランダム性が与えられます。(こちらのブログがわかりやすいです)
・分岐変数選択
決定木はCART法に基づいて生成されます。変数の条件によってふしが分岐し、どんどん成長していくのがCART樹木です。(以前の記事を参考にどうぞ)
ここで分岐条件として使用する変数をランダムに選択します。データセットにおける変数がP個、使用変数を$\tilde{P}$個とすると、$\tilde{P}\leq{P}$が成立します。$\tilde{P}$が多すぎると樹木間の相関性が大きくなってしまい、ランダム性が減少する一方で、少なすぎると決定木が十分に成長できない、予測確度の減少の原因となってしまいます。目安としては、回帰問題の時は$\tilde{P}=\sqrt{P}$
、分類問題の時は$\tilde{P}=P/3$と言われています。
ランダムフォレストでは基本的に樹木を最大まで成長させ、刈り込みをしません。停止ルールとなるパラメータは最小ふしサイズ(各ふしにおける個体数)のみなので、このサイズに依存して樹木の大きさは決まります。各ふし$t$における個体数$N(t)$について、回帰問題では$N(t)\leq{5}$、分類問題では$N(t)\leq{1}$が推奨されています
これらのルールに従って生成された決定木をを用いて、回帰の場合は平均を、分類の場合は多数決方式で解が求められます。
ランダムフォレストのアルゴリスム
ブートストラップ回数を$B$とします。(B個の決定木を生成する)
$b=\{1・・・B\}$ として、
ブートストラップ標本$\varphi^{(b)}_{boots} = \{(y_n,\textbf{x}_n), n=1,2,・・・N\}$を生成します。
$\varphi^{(b)}$を用いて、CART樹木$T^{(b)}_{max}$を生成します。この時の条件は下記の通りです
・ふし$t$の分岐には、ランダムに選択された$\tilde{P}$個の変数のみを用いる
・樹木の前進過程(成長)のみで刈り込みは行わない
・分枝の停止基準には、各ふし$t$における個体数$N(t)$のみを用いる
生成されたCART樹木$T^{(b)},b=\{1,2・・・B\}$を用いて推定モデル$h(\textbf{x};\phi^{(b)})$を生成します。
回帰、分類においてのモデル$\hat f^{(R)}_{RF}$の導出は以下の通りです。
$・回帰:\hat f^{(B)}_{RF}=\sum_{b=1}^Bh(\textbf{x};\phi^{(b)})/B$
$・分類:\hat f^{(B)}_{RF}=argmax_{1\leq{k}\leq{K}}\{\sum_{b=1}^B𝟙(h(\textbf{x};\phi^{(b)})=k)\}$
回帰はブートストラップの回数Bで平均を取る、分類は集合$1\leq{k}\leq{K}$の中で最も多いものを返す多数決となっています。
Out Of Bag (OOB)
ランダムフォレストでは、ブートストラップの際に重複を許してサンプリングすると言及しました。ということは選択されていない標本もあるわけです。この選ばれなかったデータ群をOOB(Out-Of-Bag)と呼び、ランダムフォレストの予測誤差の測定に使われます。
全体のサンプル数を$N$、選ばれなかったサンプル数を$N_{out}$とすると、$N_{out}/N$は約0.33となることが知られています。
こちらの記事で理論まで丁寧に説明されているので詳しく知りたい方はご参照ください。
Rでの実装
回帰問題でやってみます。使用データはBOSTON住宅価格のデータセットを使用します。
data(Boston)
> Boston %>% head
crim zn indus chas nox rm age dis rad tax ptratio black lstat medv
1 0.00632 18 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98 24.0
2 0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14 21.6
3 0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03 34.7
4 0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94 33.4
5 0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33 36.2
6 0.02985 0 2.18 0 0.458 6.430 58.7 6.0622 3 222 18.7 394.12 5.21 28.7
目的変数は住宅価格($1000単位)の中央値であるmedvです。randomforestはこのようにデータが揃っていれば関数一発でモデルができます。
> install.packages("randomforest")
> library(randomforest)
> randomForest(medv~.,data=Boston)
Call:
randomForest(formula = medv ~ ., data = Boston)
Type of random forest: regression
Number of trees: 500 #決定木数(デフォルト500)
No. of variables tried at each split: 4 #決定木使用する変数の数(デフォルトは回帰ではP/3, 分類ではsqrt(P))
Mean of squared residuals: 9.923244 #平均二乗残差
% Var explained: 88.25 #変数説明度
決定木の数はパラメーターntree, 使用変数の数はmtryで変更できます。例えば決定木1000本、使用変数3つにすると
> randomForest(medv~.,data=Boston,ntree=1000,mtry=3)
Call:
randomForest(formula = medv ~ ., data = Boston, ntree = 1000, mtry = 3)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 3
Mean of squared residuals: 10.67376
% Var explained: 87.36
平均二乗残差、変数説明度共に下がったので精度としては低下していますね。デフォルトの方がモデルとしては良さそうです。
rf <- randomForest(formula = medv ~ ., data = Boston)
plot(rf)
これで平均二乗残差の挙動、モデルが収束しているかどうかを確認する学習曲線(Learning Curve)を見ることができます。
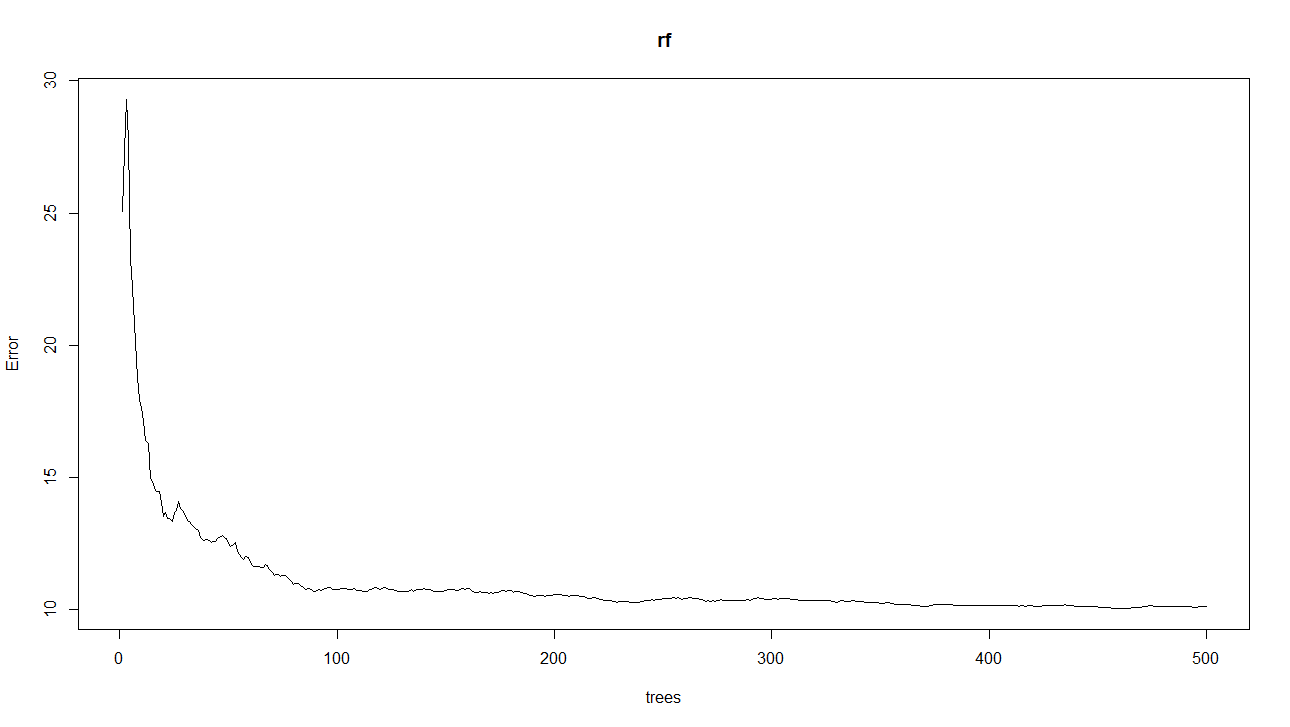
横軸が決定木数、縦軸が平均二乗残差です。500本でしっかりと収束していますね。
Bostonデータを学習用と検証用に分けてランダムフォレストで予測してみましょう。
> nrow(Boston)
[1] 506
> idx_train <- sample(1:nrow(Boston),350)
> train_Bos <- Boston[idx_train,]
> test_Bos <- Boston[-idx_train,]
> nrow(train_Bos) + nrow(test_Bos)
[1] 506
> nrow(train_Bos)
[1] 350
> nrow(test_Bos)
[1] 156
506データのうち、350個を学習用データ(train_Bos)、156個を検証用データ(test_Bos)に分割して生成しました。train_Bosを用いてモデリングします。
rf_trainという変数にモデルを格納して、検証データで予測してみましょう。
> rf_train <- randomForest(medv~.,data=train_Bos)
> rf_train
Call:
randomForest(formula = medv ~ ., data = train_Bos)
Type of random forest: regression
Number of trees: 500
No. of variables tried at each split: 4
Mean of squared residuals: 13.47639
% Var explained: 83.56
> pred_rf <- predict(rf_train,test_Bos)
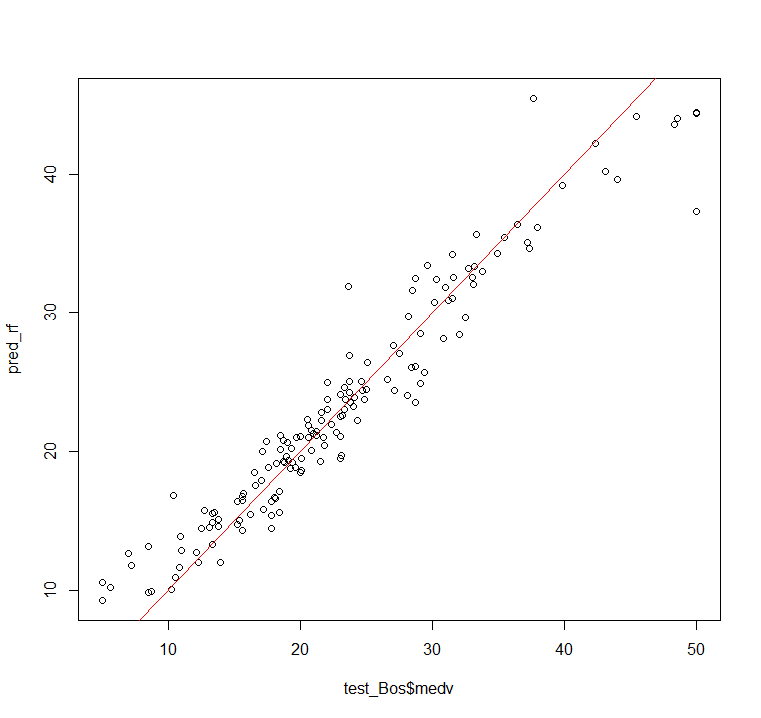
pred_rfには予測データ156個の予測値が格納されています。実際のtest_Bosのmedv値とpred_rfの予測値を比較してみましょう。
> RMSE(pred_rf, test_Bos$medv)
[1] 2.597209
# 実測値(横軸)と予測値(縦軸)をプロットで描写
> plot(test_Bos$medv, pred_rf)
# y=xの直線(同じ値であれば線上に点がくるはず)
> abline(0,1,col="red")
平均二乗残差;RMSEが約2.6、可視化すると上の図のようになりました。なかなかの精度で予測できているのではないでしょうか?
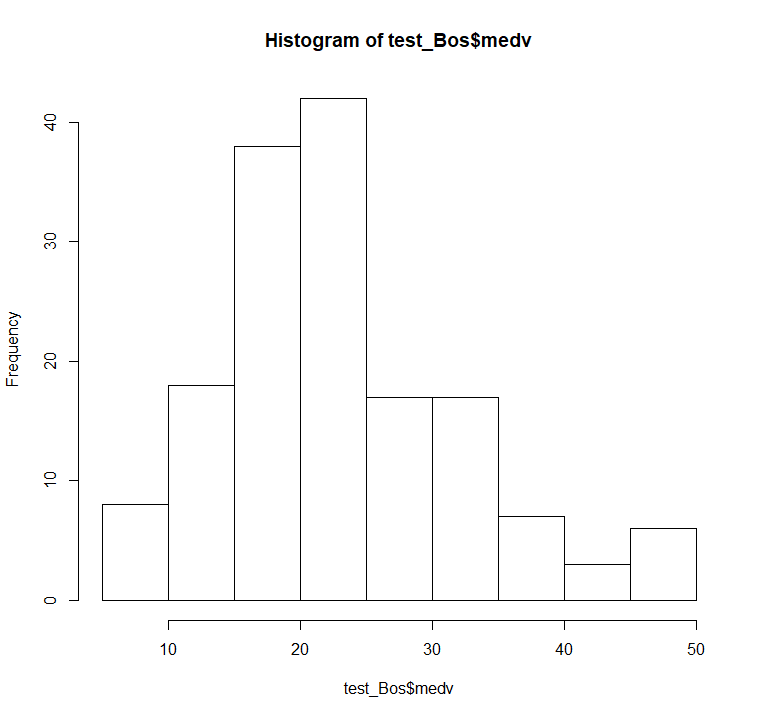
しなみにこのRMSE本データにのおいて大きいのか小さいのかの一つの目安にするために、medvの分布を確認してみましょう。
# medvの要約統計量
> summary(test_Bos$medv)
Min. 1st Qu. Median Mean 3rd Qu. Max.
5.00 17.35 21.75 23.13 28.70 50.00
# medvの分布
> hist(test_Bos$medv)
5~50に分布し、それぞれのビン(5区切り)に少なくとも5くらいはカウントされているち考えると、2.6というRMSEは良い線行っていると考えて良さそうなのでは?と思います。
ランダムフォレストってRだと簡単でした。だけど・・・
Rだと上記コードを実行するだけでモデリング、予測値を返すことができたのですごく簡単でしたね。だけどその裏にあるアルゴリズムをしっかり押さえておかないとなんでランダムフォレストが外れ値に頑健なの?とか、学習曲線も見ておかないと、そのモデルって妥当なの?ってところから考えないといけないので、ただコーディングするだけじゃなくてしっかりと理論的なところも勉強してこそ実務で役に立つんじゃないかなっていうのが個人的な感想です。(機械学習全般においての話)
ランダムフォレスト最強説(ディープラーニング除く)も巷ではあるようですが、なぜ最強なのかとか自分なりの根拠も持ち合わせてからこういう事は説きたいですね。