超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)⓪
超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)①
超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)②
超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)③ Rで作る回帰決定木
もどうぞ
一本の決定木(Tree)の話から、複数の決定木(Forest)の話です。
ランダムフォレストに行く前に、決定木を使った機械学習手法について整理してみましょう。
アンサンブル学習ってなに?
弱い学習器(ここではCART樹木)の結果を統合して、強力な予測を行う委員会(commitee)を構成することであり、ブースティングとブートストラップに大別されます。よく言われるのは「3人寄れば文殊の知恵」ってやつですね。ランダムフォレストはブートストラップの方に分類されます
なんでアンサンブル学習使うの?決定木じゃだめなの?
所謂決定木というのは、一本の木しか生成していません。これまでの紹介してきたCART樹木を例にすると
・メリット:分類・回帰共に使えて説明変数のコード化が必要ない。視覚的にもわかりやすく様々な尺度の変数を使用できる。
・デメリット:学習データに依存して過学習しやすい、他の線形モデル等に対して予測精度が良くない、データセットや変数が大きいほど計算コストの増大と過学習が生じやすい
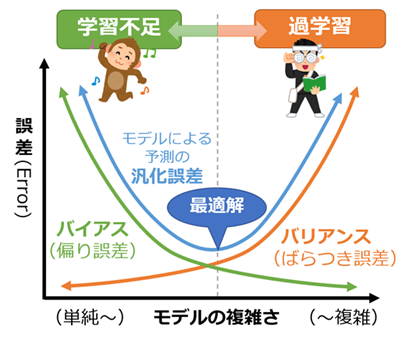
一本だけの木でモデリングしているのでそりゃ過学習も起きますよね。別の言い方をすると、小バイアス(偏り)と大バリアンス(分散)が生じます。このバイアス・バリアンスのバランスを取って汎化性能を向上させるのが機械学習の肝です。(と思ってます)
ちなみにこの辺については以下サイトで詳しく説明してありますので参考にどうぞ。
https://www.atmarkit.co.jp/ait/articles/2009/09/news025.html
https://towardsdatascience.com/decision-trees-understanding-the-basis-of-ensemble-methods-e075d5bfa704
アンサンブル学習で複数の決定木を組み合わせることで、バリアンスを減らすことができ、理想的なモデルに近づきます。この時逆にバイアスは増大し、この2つはトレードオフの関係となっております。
それぞれの決定木でモデリングのされ方が異なっているので、予測精度は向上しますし、外れ値やノイズの影響も少なくなるためモデルの頑健性(Robustness)も改善します。まさに三人寄れば文殊の知恵です。
アンサンブル学習の種類
ブースティング
一本の決定木からスタートし、そこからの結果と予測誤差を逐次に改善し、修正を重ねることで修正を重ねた標本がつくられます。
分類、回帰問題の両方に適用できます。しかし一般的に学習に時間がかかるのが欠点です。
というのも決定木$1$→決定木$2$→・・・決定木$n$と一つずつ直列的に結果の出力と修正を繰り返すのでそれを何百回と繰り返すとかなりの計算コストがかかります。
手法の例としては古典的なAdaboost、MART法勾配:勾配ブースティング(GBM)や発展的なXgboost、Light gbmなどでしょうか
ブートストラップ
直列だったブースティングとは異なり、ブートストラップ法は並列的に、独立的に樹木を構成できます。
予測確度はブースティングに劣るといわれていますが、外れ値に対して頑健であり、計算コストも少なく済みます。
また、こちらもブースティング同様分類・回帰問題の両方において高い予測精度が得られます。
手法の例としてはBagging法やランダムフォレストが挙げられます
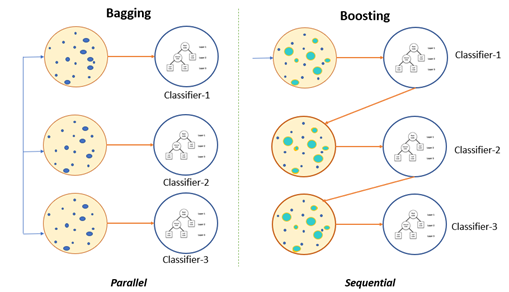
イメージこんな感じです(左がブートストラップ、右がブースティング)
https://seongjuhong.com/2021-01-17pm-ensemble-bagging-and-boosting/
それぞれ特徴があるので、どちらが良いとは一概に言えないとは思います。予測精度、ノイズの多さや目的(汎化性能を求めるのか、とにかく誤差を少なくするのか、とか)によって手法を選べるように基本的なアルゴリスムは学んでおきたいですね。
次回はいよいよランダムフォレストについての記事に突入予定です。