背景
初めまして、初投稿です。2021年1月より運と勢いだけで、全くの初心者としてとあるメーカーの社内データアナリストとして働き始めました新参者です。
会社で与えられた、最初に理解すべきアルゴリズムがランダムフォレストということで、参考書籍をベースに備忘録も含めて少しずつ記事として形に残したいと思い投稿しました。
参考書籍として、主に樹木構造接近法 (Rで学ぶデータサイエンス 9)を使用予定です。
目的
一番はアルゴリズムの理解です。なので意味不明な数式や用語の理解についても積極的に考察していきます。
言語はRを用いていますが、目的はあくまでもアルゴリズムの理解なので他言語やソフトウェアを使っている方にも少しでも参考になるような記事を書ければと思います。
モデルにぶち込み結果を得るだけでなく、変数の意味やモデリングの際の注意点等にもこの勉強を通して新たな発見や洞察を得ることが本質なので冗長な点が多々あると思いますがご了承ください。
週2くらいで投稿したいなという心持です。
本題
ランダムフォレストについてなんとなく知っていることですが・・・
・回帰も分類もできる！アンサンブル学習（意味よく知りません）の典型！
・回帰は平均、分類は多数決で解が求まる！
・数値やカテゴリーで区分して枝を作っていく！
・なんか不純度やらジニ係数なるものがあるらしい
・たくさんの決定木を作ってブースティングやらブートストラップサンプリングやらといった手法で弱学習器を重ねて強いものにするっぽい
こんなふわっとした物をしっかりと体系的に固めていきましょう
なんで樹木構造を使うのか？
樹木構造接近法とは、ランダムフォレストを含む、CART法やMARS法、PRIM法と呼ばれる分析手法の総称です。
これらの分析手法を使う主な理由としては以下の5つ
①デンドログラム（樹木）として表せるので結果解釈が視覚的に簡単
②目的変数と説明変数の非線形構造。交互作用を有意義に捉えられる
③説明変数次元（列数）＞データ数にも適用できる
④説明変数の慎重な変換（コード化）が必要ない
とのことですが、分析側にとっても受け手側にとっても取り扱いやすいって感じでしょうか。
CART法
CART法の特徴について
・説明変数の尺度が名義尺度～間隔尺度まで扱える
・応答変数が連続の場合は回帰樹木、分類変数の場合は分類樹木と呼ばれる
・樹木図は上→下へふしが分岐する（条件がTrueの場合は左へが基本）
・終結ふしの値は応答の予測値であり、回帰の場合はふしに属する個体の平均値が、分類の場合には多数決方式が用いられる
特に説明変数の尺度なんかが自由なのは、ローデータそのままぶっこめそうなのがメリットに見えますね！
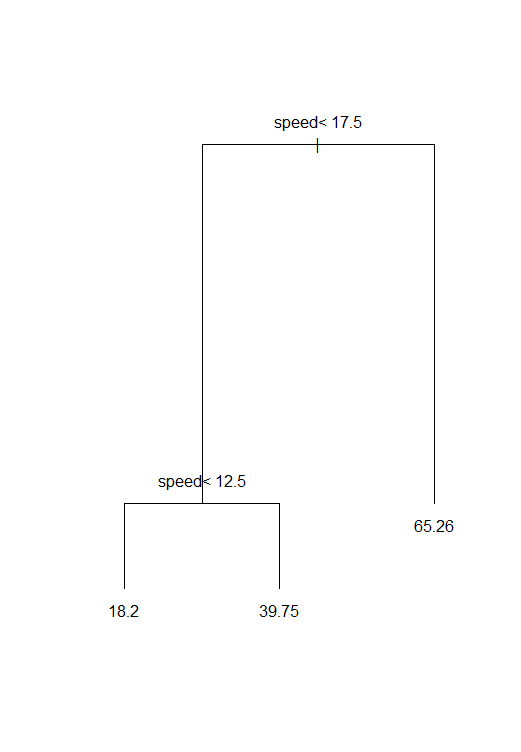
というわけで、Rに既存のcarsデータで実際に可視化すると
| speed | dist |
|---|---|
| 4 | 2 |
| 4 | 10 |
| 7 | 4 |
| 8 | 22 |
| 9 | 16 |
（以下略）
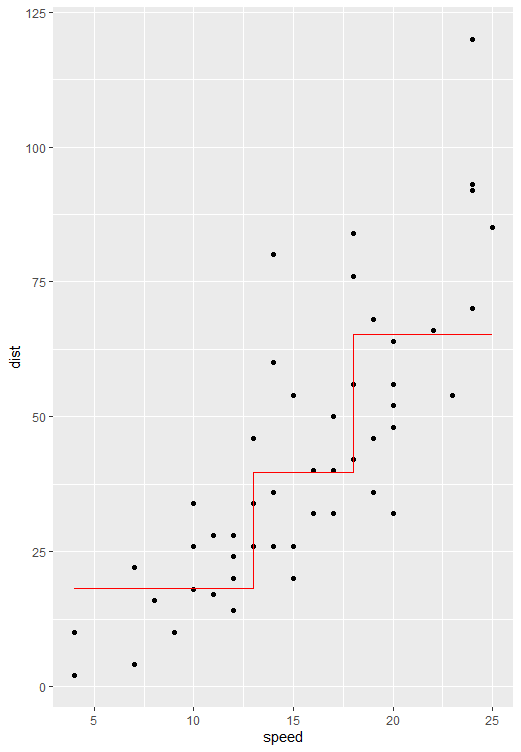
走行距離（dist）がスピードで分枝されて、平均走行距離が出力されてますね！
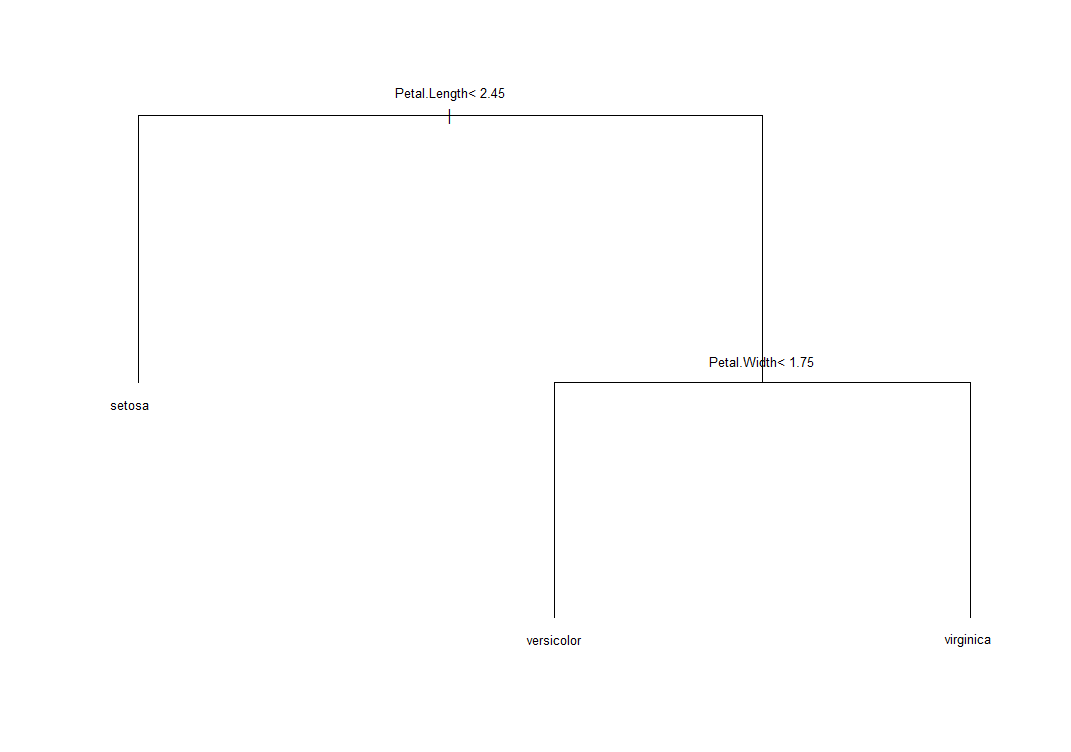
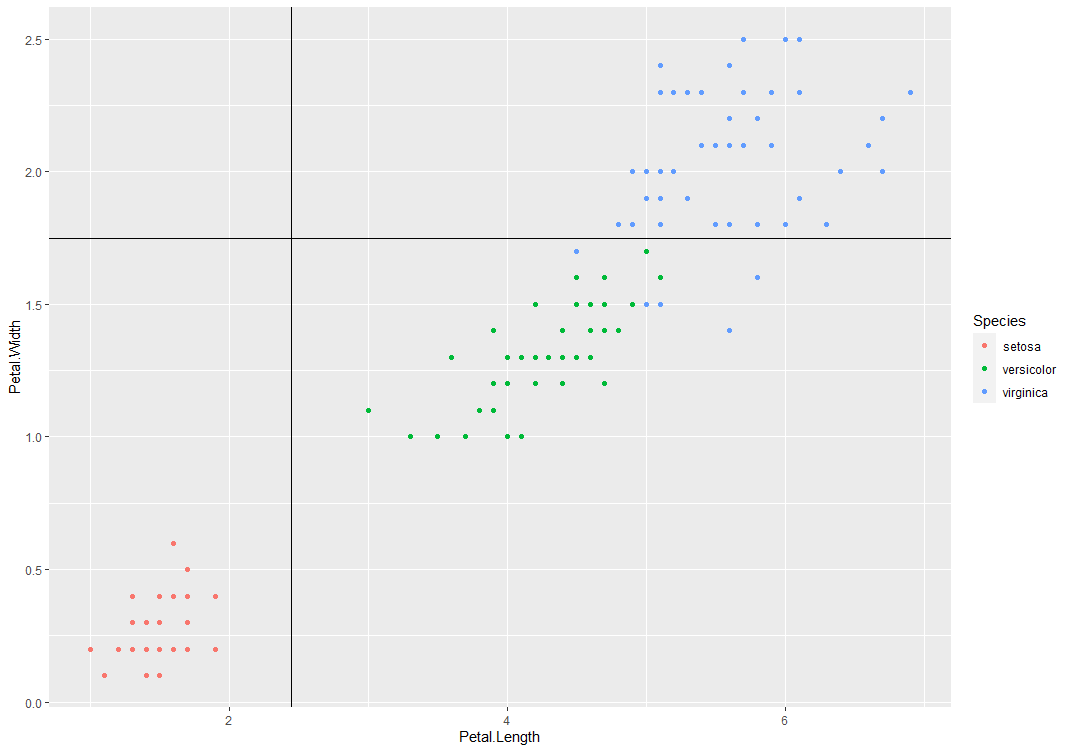
さて、分類について、irisデータでやってみると
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5.0 | 3.6 | 1.4 | 0.2 | setosa |
（以下略）
Petal lengthとPetal Widthが説明変数、Speciesが分類応答変数となっていますが、プロットを見るとなかなかよく分けられていますね。
ここまではデータをモデルに突っ込んだだけです。なんでこのような結果が出るのか、果たしてこの結果の妥当性はどうなのか？という点がこのシリーズを始めた目的。
ジニ係数や枝の刈込、サンプリング等が重要になってくるのか・・・
今回はあまりに基礎の基礎の退屈記事になってしまいましたが・・・
次回からは本格的にそこを探っていきたいと思います！