超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)⓪
超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)①
超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)②
もどうぞ
今回はいよいよ!Rコードを書いてCART法での分析を実践してみましょう!
使用データ
コード:R
使用データ:ボストン住宅価格データ (Boston housing dataset)
data(Boston,package = "MASS")
上記コードでR備え付けのボストン住宅価格データがインストールできます。
さて、説明変数に様々なデータ尺度を使えるのがCART法のメリットでもあります。データ型の概要をチェックしてみましょう。
sapply(Boston, function(x) class(x))
# crim zn indus chas nox rm age dis rad tax ptratio black lstat
# "numeric" "numeric" "numeric" "integer" "numeric" "numeric" "numeric" "numeric" "integer" "numeric" "numeric" "numeric" "numeric"
# medv
# "numeric"
sapply関数で各列のクラス型をチェックしました。
目的変数となるのはmedv:住宅価格でnumeric、連続値。回帰樹木を作ることになります。
説明変数は13個、そのうち"chas", "rad"という2項目がint型です。
"chas"はチャールズ川沿いかどうかのダミー変数、"rad"は幹線道路へのアクセスの良さを示す指標です。このように連続値ではなく離散値も一緒に扱えるところで力を発揮してますね!!
樹木作成
樹木の成長
樹木の作成はrpart関数を使用します。樹木作成は樹木の成長→刈り込み→最適樹木の選択というプロセスを踏むというお話は以前しました。
まずは樹木を大きくしてみましょう。
library(rpart)
rtree0 <- rpart(medv~., data=Boston, method="anova", control=rpart.control(cp=0))
plot(rtree0, uniform = T, margin=.1)
text(rtree0, cex=0.6)
method="anova"は回帰樹木を指します。control=rpart.control()では様々なパラメーターを設定できるのですが、cpは複雑度パラメーターαを同等です。最大樹木を作るために、とりあえずcp=0としています。(デフォルトだとcp=0.01なので注意!!)
ちなみに他のパラメーターとしては終結ふしの最小個数 (minbucket)や樹木の深さの最大値(maxdepth)等を自分で設定できます。
plot()で樹木を描き、必要な情報をtext()で加えます。
margin, cexの数字で図形や文字の大きさは適宜調節しましょう。ここで出来上がった最大樹木が下です。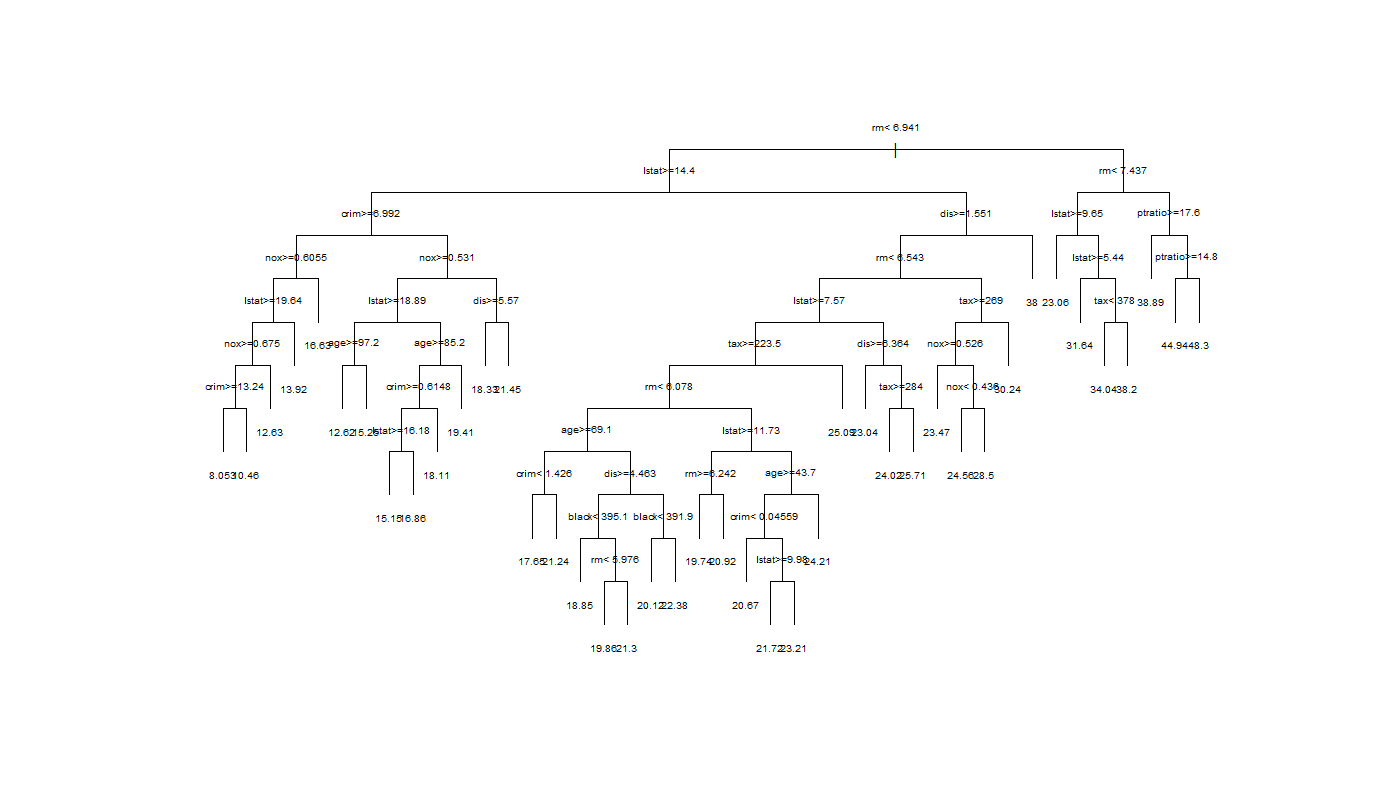
どうでしょうこの複雑さと明らかな過学習感。これは刈り込みたくなりますねぇ。
ちなみに13ある変数のうち4つは使われませんでした。残念。(赤字の項目を使用)
樹木の刈り込みと選択
樹木の刈り込み過程では、最大樹木から複雑度コスト$\alpha$に基づいて樹木列が形成されますが、そこから最適樹木を選択することになります。すなわち、最適なcp値を選択する作業が必要です。
前回の記事で説明しましたが、交差検証法を用います。通常、V=10としたV重交差検証法になりますが、この回数はxvalというパラメーターでrpart関数内で指定ができます。
$ \{ T_j \}^J_{j=0}$の樹木列に対応する交差確認推定値$R^{CV}(T_j)$の推移を見てみましょう。
plotcp(rtree0)
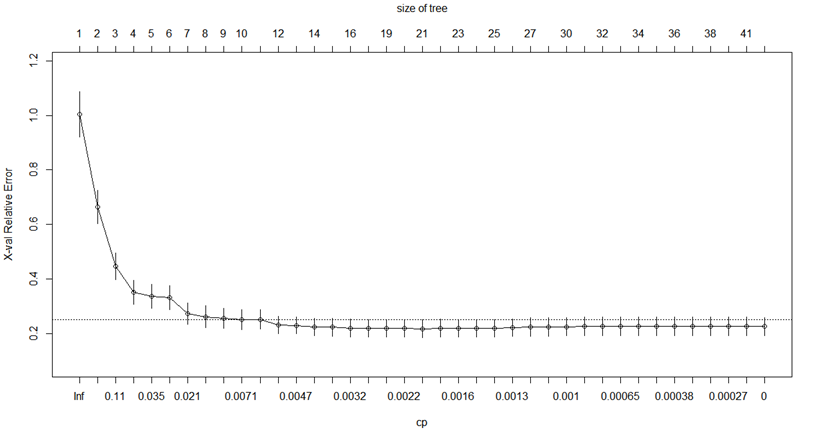
縦軸が交差確認推定値$R^{CV}(T_j)$、上軸が終結ふしの数$|\widetilde T|$、下軸がcp値です。$R(T_0)$で標準化されているので最大値は1になります。横向きの点線は、最小の交差確認推定値+1SEを$R(T_0)$で割り、標準化したものを示しているそうです。すいませんこの辺私もよく理解できていないので頭良い人は教えてください。
樹木列の詳細について知りたい場合、次のコードで見られます。
rtree0$cptable
# CP nsplit rel error xerror xstd
# 1 0.4527442007 0 1.0000000 1.0082499 0.08346677
# 2 0.1711724363 1 0.5472558 0.6098660 0.05609355
# 3 0.0716578409 2 0.3760834 0.4166808 0.04584099
# 4 0.0361642808 3 0.3044255 0.3608869 0.04364964
# 5 0.0333692301 4 0.2682612 0.3435650 0.04373716
# 6 0.0266129999 5 0.2348920 0.3294935 0.04396666
# 7 0.0158511574 6 0.2082790 0.3123605 0.04230403
# 8 0.0082454484 7 0.1924279 0.3061785 0.04319710
# 9 0.0072653855 8 0.1841824 0.2934061 0.04270719
# 10 0.0069310873 9 0.1769170 0.2973287 0.04281932
rel errorが再代用推定値$R(T_j)$、xerrorが交差確認推定値$R^{CV}(T_j)$、xstdは標準誤差の推定値です。xerrorが最小のCP値を見つけることが最適樹木の選択につながります。
さて、どうすれば良いのか・・・・・
高々42ふしまでのデータなので目視で確認できないこともないですがスマートではありません。Rにはwhich関数という、インデックスを取得できる便利なものがあるのでそれを利用してxerrorが最小のインデックスを取得して、そこからcp値を求めましょう。
j0 <- which.min(rtree0$cptable[,"xerror"])
rtree0$cptable[j0,]
# > j0
# 19
# CP nsplit rel error xerror xstd
# 0.002172094 19.000000000 0.137388272 0.262178796 0.041065605
19列目のcp=0.002172094が最適樹木となりました!さあ先ほどと同じ手順でcp=0.002172094として樹木を作ってプロットしてみよう!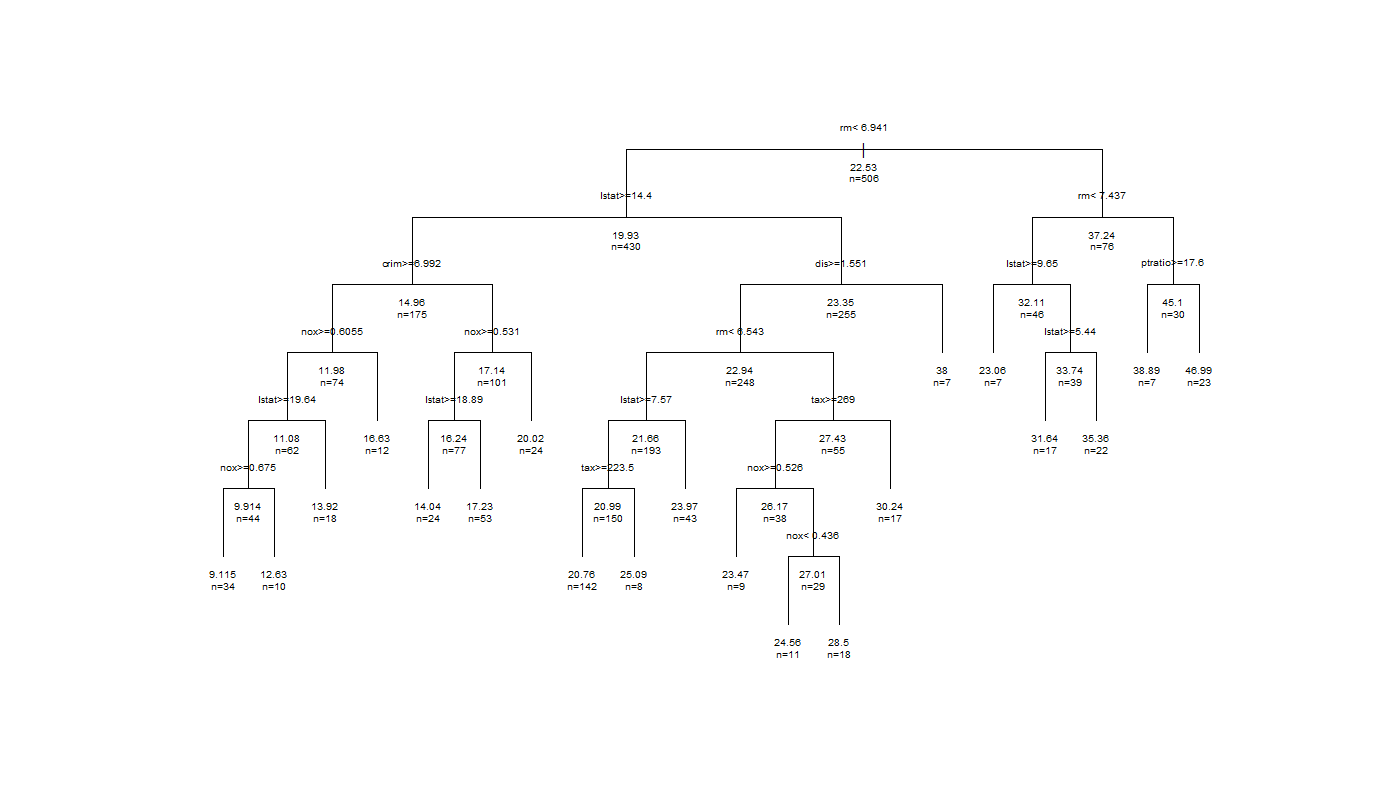
あれ、まだ複雑じゃないか・・・
こういう時は1SEルールの適用です。関数を作らなければいけないので少し複雑ですが解説していきます。
one_se_rule <- function(tree){
j0 <- which.min(tree$cptable[, "xerror"]) #最小xerrorのインデックス取得
Rcv.min <- tree$cptable[j0, "xerror"] #上で取得したインデックスのxerrorを取得
one.se <- tree$cptable[j0, "xstd"] #上で取得したインデックスのxstd(標準誤差:SE)を取得
j1 <- 1
while(tree$cptable[j1, "xerror"] > Rcv.min + one.se) #1列目から順に1SEルールを満たすまでwhile構文で回す
{j1 <- j1 +1}
return(tree$cptable[j1,])
}
out_1se <- one_se_rule(rtree0) #最大樹木からの1SEルールに基づいた刈り込みで得られる最適樹木のデータを格納
>out_1se
# CP nsplit rel error xerror xstd
# 0.007265385 8.000000000 0.184182405 0.293406073 0.042707192
1SEルールについて復習しましょう。
$R^{cv}(T_{j1})\leq R^{cv}(T_{j0}) + \widehat {SE}(R^{cv}(T_{j0}))$
を満たす$T_{j1}$を見つけるのがこの関数の目的です。while構文内ではこの式を満たすj1が現れるまで、計算を繰り返し、これを満たしたインデックスのデータtree$cptable[j1,]を返すわけです。
そしてそのデータを変数out_1seとして格納しました。
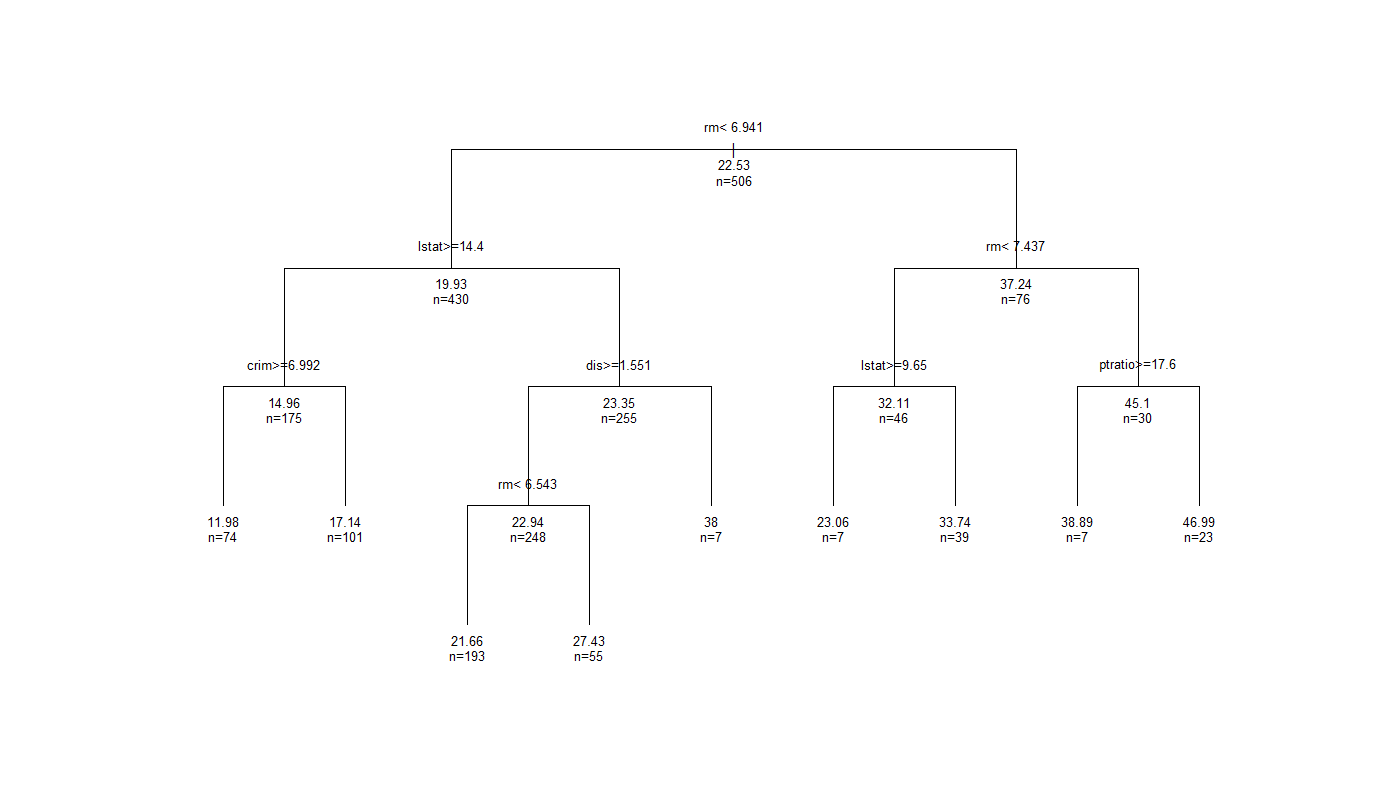
この得られたcp値に対応して刈り込まれたデータを描いてみましょう。
rtree_1se <- prune(rtree0, cp=out_1se["CP"])
plot(rtree_1se, uniform=T, margin=.1)
text(rtree_1se, use.n=T, all=T, cex=.8)
かなり見やすくなりました!ちなみに引数use.nはふし内の個体数の表示、allは終結ふしだけでなく途中のふし情報をの表示の有無を選択しています(デフォルトは両方FALSE)
ちなみに・・・
使われた説明変数ですが、最大樹木で9→最小の再代用推定値で7→1SEルールで5と、樹木が簡単になるにつれて減少しています。この辺も変数選択のコントロールはできるんですかね~、興味があります。
描き方いろいろ
plot()のところ、uniform=FALSEとすると、リスクの再代用推定値の減少量が枝の長さに反映されます。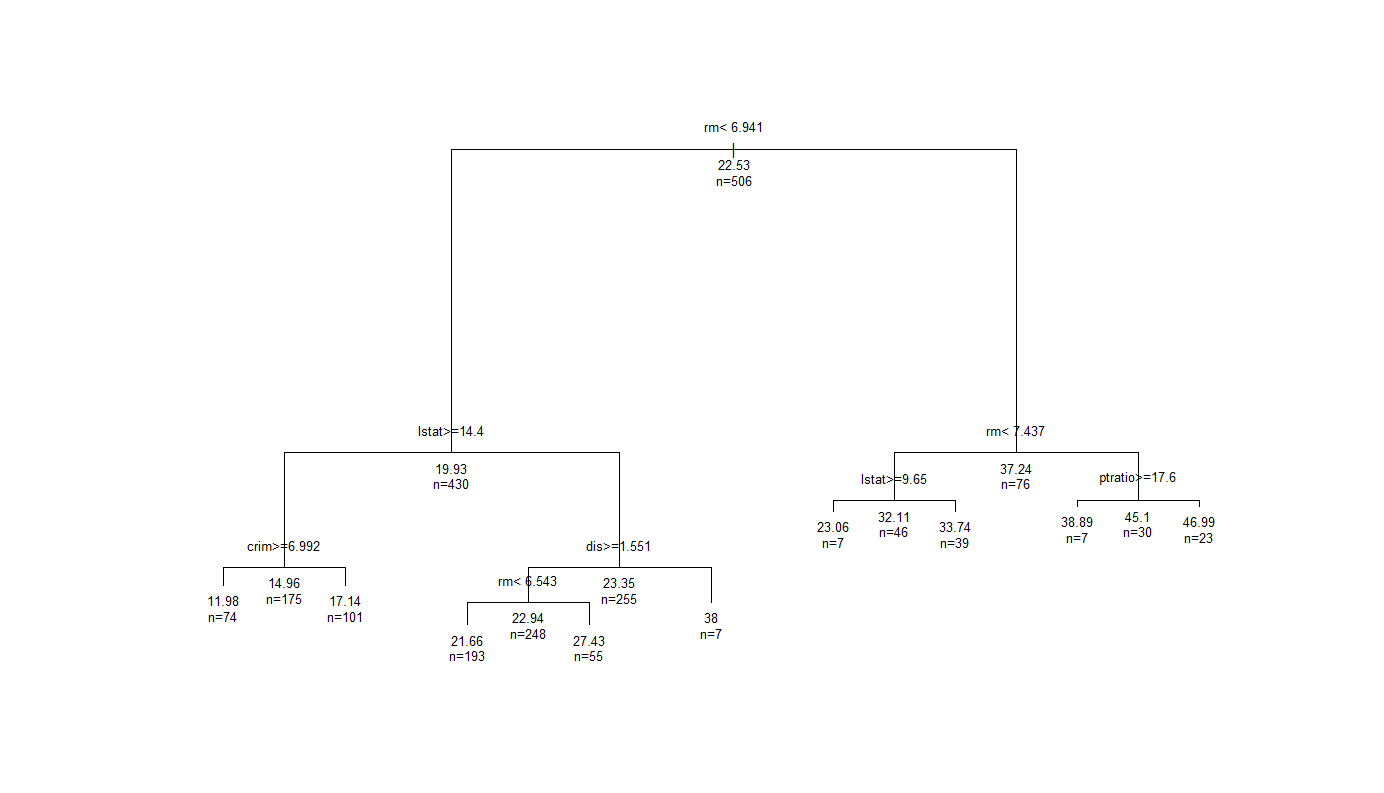
ここは好みですね(笑)
partykitパッケージを使うと視覚的なインパクトが強くなります
install.package("partykit")
library(partykit)
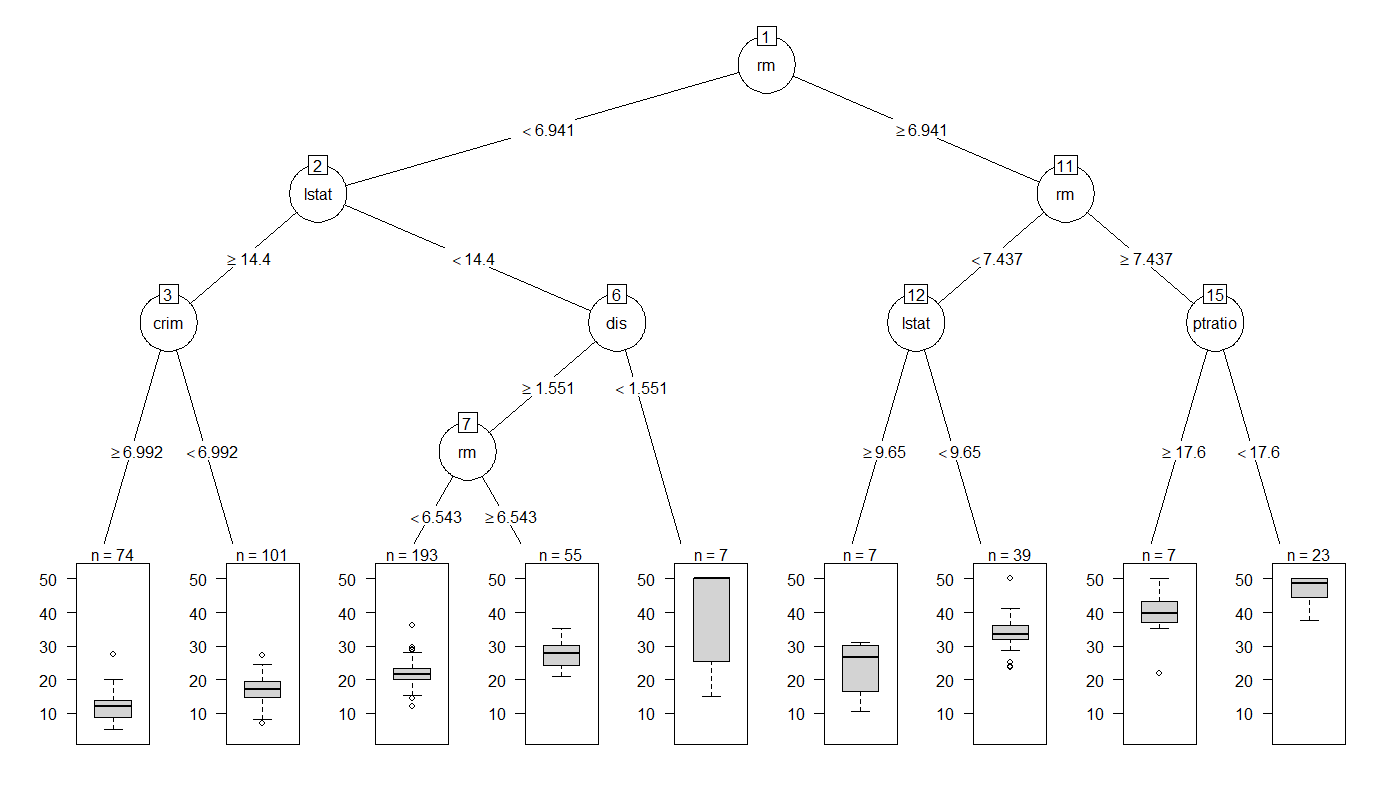
plot(as.party(rtree_1se), tp_args = list(id=F))
分岐条件の表示位置が変わり、終結ふしでは箱ひげ図が現われるので分布も確認できます。それぞれのふし内の特徴を一目でつかめるので便利ですね!
CART法による予測
今回学習したモデルでの予測は他の回帰モデル同様、predict()関数を用います。
実測値と比較してみましょう。
pred_value <- predict(rtree_1se, newdata = Boston)
limit <- range(Boston$medv)
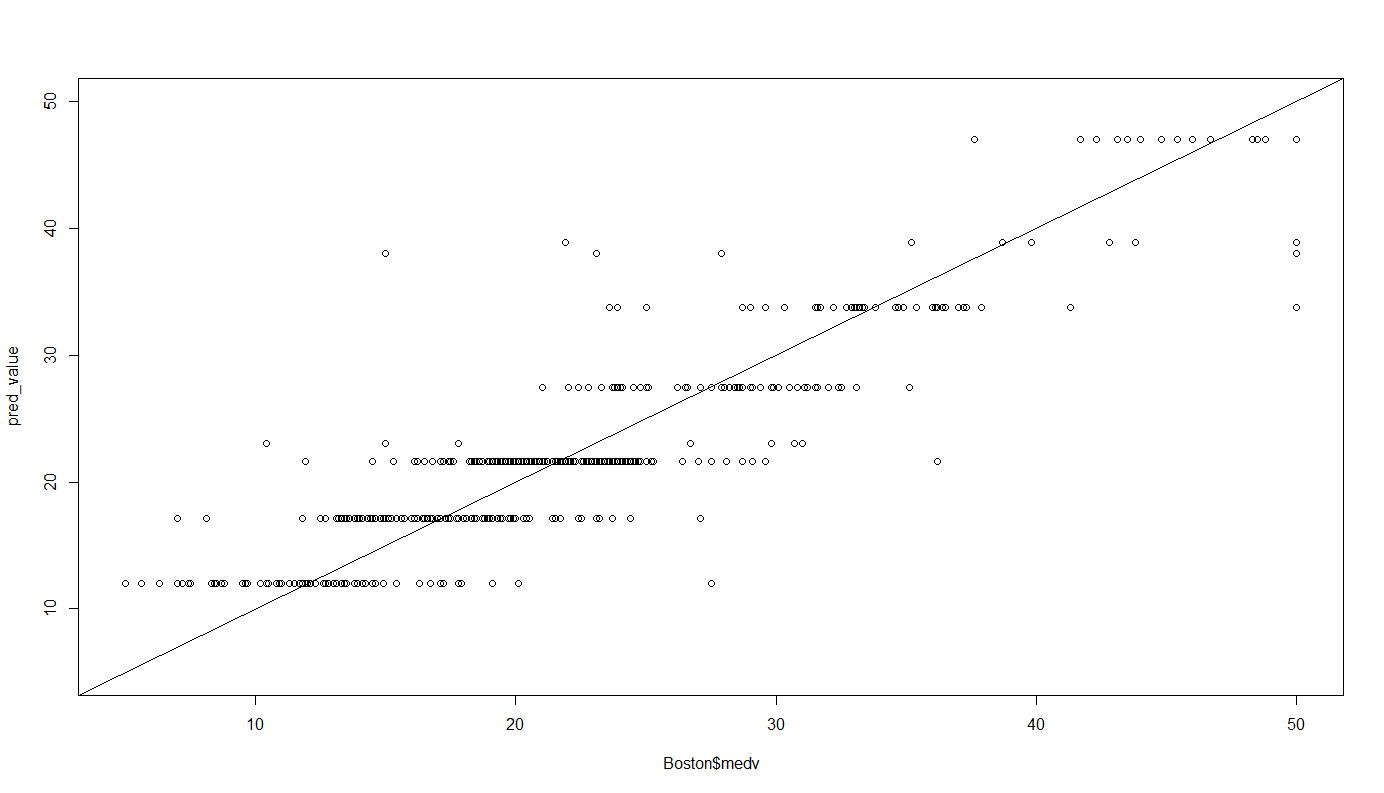
plot(Boston$medv, pred_value, xlim = limit, ylim = limit)
abline(0,1)
テキストに則るとこっちなんですけど、個人的にはggplotの描画が好きなので勝手にかいてみます。
pred_value <- predict(rtree_1se, newdata = Boston)
cbind(Boston$medv, pred_value) %>% data.frame() %>%
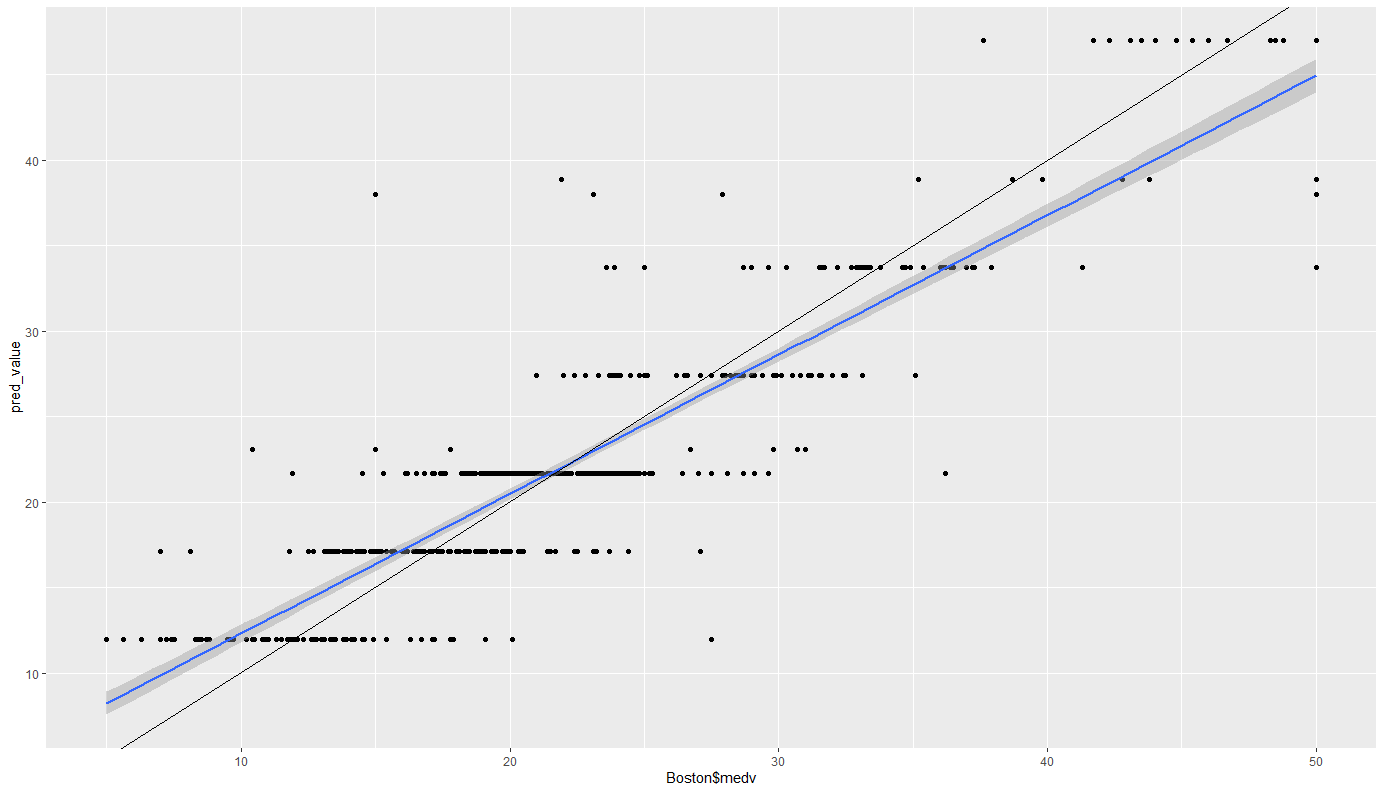
ggplot(aes(Boston$medv, pred_value)) + geom_point() + geom_smooth(method="lm") +
geom_abline(slope = 1, intercept = 0)
青が回帰直線、黒がy=xの直線です。
こう見ると大まかな傾向は捉えられていますね。しかし応答ふしが9つしかないため、どうしてもばらつきが大きくなりがちです。
このことがCART法の予測精度が低いといわれる所以でもあります。
しかし、別の観点からみると、どのような説明変数の影響で応答が分かれるのかを探索してみたり、単なる予測だけではなくデータの深堀や考察にも今回作った決定木を使ってみると面白そうですね!!
次回は分類の決定木についてです!