超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)⓪
超初心者が学ぶランダムフォレスト・分類回帰樹木 (CART法)①
もどうぞ
前回が重すぎてヘロヘロなので、今回はあまり知られてないであろうと思われる、ポアソン回帰樹木 (Poisson) について簡単に取り上げてみようと思います。
ポアソン回帰の前に
ポアソン分布ってなに?
ポアソン分布は0以上の正のカウント数に基づくモデリングでよく使われる分布です。例えば、時間当たりの交通量とか、小売店の利用客とか、非連続でカウントできて、その上限が不明なものが応答変数になるのが特徴です。
ポアソン分布のパラメーターは一つだけ、$\lambda$です。参考程度ですが、統計的にはポアソン分布は$平均=分散=\lambda$であることが知られています。
ポアソン分布は
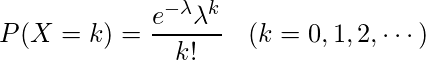
の式で表される確率分布に従います。ここで$\lambda$はパラメーター、$k$は、その現象の発生回数です。つまり、平均発生回数が$\lambda$である事象が$k$回起こる確率を示しています。
詳しくは統計学の時間さんがおすすめです。
ポアソン回帰樹木
このポアソン分布を樹木に応用してみましょう。
応答$y$及び説明変数$x$があるときに、$y$が以下のポアソン分布に従うと仮定します。
$\large Pr(Y=y)= \frac{exp(-\mu)\mu^y}{y}$・・・(*)
この仮定のもとで、($y \sim Poisson(\lambda)$)と、yが従う時に、ポアソン回帰に基づくモデルは
$\log(\mu)=f_{GLM}(x)$
で与えられます。これはポアソン分布を用いて一般化線形モデルと呼ばれる回帰式に変形したもので、yを説明変数xの線形予測式で表すことができます。ポアソン回帰の場合は通常、
$\log (\lambda)=\beta_0+\beta_1x_1$
のような形式です。言い換えると行列$\bf{x^T}$βです。詳しくは緑本やbiostatisticsさんを参考にどうぞ。
Poisson回帰樹木では、ふし内に複数個体が含まれています。ふし$t$内の母平均$\mu(t)$の推定値は、通常の回帰樹木と同じく平均を取るので、
$\hat\mu(t)=\frac{\sum_{n\in t}y_n}{N(t)}$
で与えられます。
通常の回帰樹木と違い、注意が必要なのは不均一性測度です。ポアソン回帰樹木の場合は、変分(逸脱度: deviance)に基づく尤度の変分残差を用います。その式は
$r_{P_0}(t)=2\sum_{n\in t}\{y_n\log(y_n/\hat\mu(t))-(y_n-\hat\mu(t))\}$
で表されます。私も理解が完全ではないのですが、分解して考えてみましょう。
逸脱度は、$D=-2\log(L)$で表されます。この時$L$は尤度です。
そして、尤度は
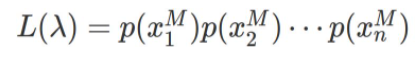
で表されます。(参考:理数アラカルト)
各$x_n$の値で得られる確率密度をかけ合わせた値ですね。
ポアソン分布ではこれを対数変換した対数尤度関数が扱われ、$\log L(\lambda)$で与えられます。先ほど(*)で定めた式の右辺を対数変換してみると
$\log (\lambda)=$$-\mu + y\log\mu-\log y$・・・★
と分解できますね。
ここで、偏分残差による不均一性測度と逸脱度に立ち返りましょう。
偏分(逸脱度)の残差、Deviance residualsは
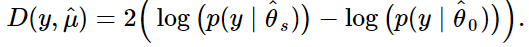
で与えられます。(参考(英語です):[Interpreting GLM]
(https://www.datascienceblog.net/post/machine-learning/interpreting_generalized_linear_models/))
これ$r_{P_0}(t)$と同等になってほしいのです。
ここで$\hat \theta_s$が最大尤度、$\hat\theta_0$が予測モデルの尤度とします。
★で定めた式を、各nで足し合わせた物が対数尤度$L_n$になることを利用すると、上式に当てはめて
$2(\log(L_{y_n})-\log(L_{\hat\mu(t)}))$
$=2\{\sum_{n\in t}(-y_n + y_n\log y_n-\log y_n)-\sum_{n\in t}(-\hat\mu(t) + y_n\log\hat\mu(t)-\log y_n)\}$
$=2\sum_{n\in t}\{y_n\log (y_n/\hat\mu(t))-(y_n-\hat\mu(t))\}$
$=r_{P_0}(t)$
となりました。
以降の樹木の成長過程、刈り込み過程、交差確認法の流れは以前までと同じです。
テキスト(Rで学ぶデータサイエンス9)に式の導出がのってなかったので、持てる知識を総動員して試みてみましたが、間違い等ございましたら、ご指摘くださると幸いです。
こうやって見ると、機械学習のアルゴリズムを理解するのにも高度な統計的知識が求められますね。まだまだ勉強が必要です。
次回からは実際にRコードで動かしてみましょう!!