More than 1 year has passed since last update.

LEGO 部品を利用した回転型倒立振子のレシピを公開！（第 3 回：運動方程式ー MATLAB / Symbolic Math Toolbox）

Last updated at 2022-12-27Posted at 2022-06-05

YouTube 「かーたー」チャンネル

LEGO 部品を利用した回転型倒立振子のレシピを公開！

第 1 回：組み立て
第 2 回：電子工作
第 3 回：運動方程式 ― MATLAB / Symbolic Math Toolbox
第 4 回：パラメータ同定 ― MATLAB / Simulink
第 5 回：現代制御 ― MATLAB / Simulink　…… 未完成
第 6 回：アドバンスト制御 ― MATLAB / Simulink　…… 未完成

おまけ

Simulink の分岐処理を利用して『回転型 LEGO 倒立振子』を振り上げ安定化！

補足

1. はじめに

　倒立振子は不安定なシステムであるため，適当にコントローラのパラメータを決めても倒立させることは困難です．そこで，倒立振子のふるまいを表現するモデルを微分方程式で記述し，このモデルに基づいてコントローラを設計することにより，倒立振子を倒立させることを目指します．
　今回は，回転型倒立振子の「運動方程式」（微分方程式）を導出する手順について説明します．

2. ラグランジュ法による運動方程式の導出

2.1　ラグランジュ法とは？

　機械系のモデルは運動方程式で記述されます．運動方程式といえば，ニュートン (Newton) の第 2 法則に現れる

\begin{align}
Ma = F
\end{align}

を思い浮かべるのではないでしょうか．単純なシステムであれば，ニュートンの運動方程式を利用すれば良いのですが，回転型倒立振子は少々，複雑です．このような場合，ラグランジュ (Lagrange) の運動方程式を利用することが多いです．

　この方法では，まず，システムの各エネルギー

運動エネルギー：$K$
位置エネルギー：$U$
散逸エネルギー：$D$

求め，ラグランジアン $L = K - U$ を計算します．そして，ラグランジュの運動方程式

\begin{align}
	\dfrac{{\rm{d}}}{{\rm{d}}t}\biggl(
		\frac{\partial{L}}{\partial\dot{q}_{i}}
	\biggr)
	- \frac{\partial{L}}{\partial{q}_{i}}
	+ \frac{\partial{D}}{\partial\dot{q}_{i}}
	= {Q}_{i}
	\quad
	(i = 1,\,2,\,\ldots,\,N)
	\tag{1}
\end{align}

に代入します．ここで，$N$ は質点の数，$q_i$ は一般化座標（質点の位置や角度），$Q_i$ は一般化力（質点に加わる力やトルク）です．　

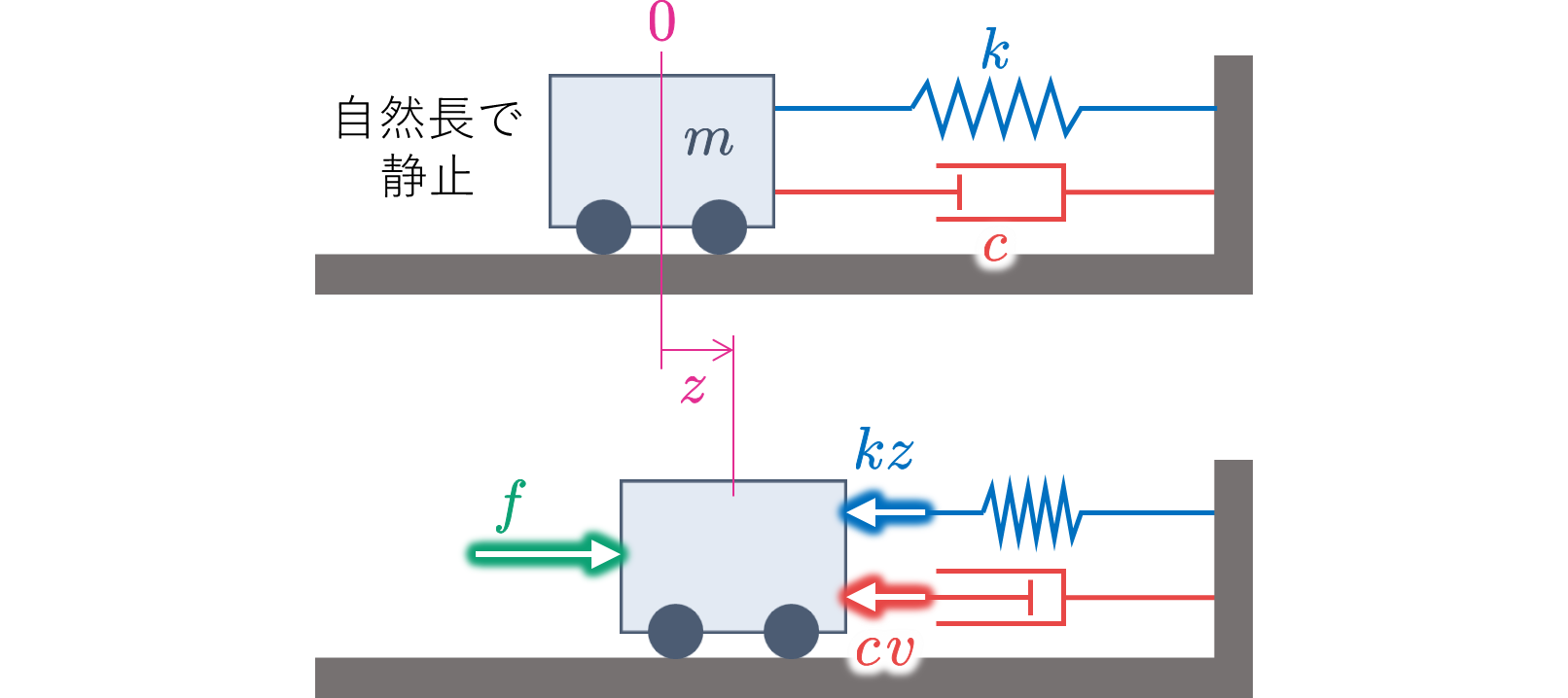
【マス・ばね・ダンパ系の運動方程式】

　マス・ばね・ダンパ系を考えてみましょう．ニュートンの運動方程式を利用すると，
$$ma = \underbrace{f - kz - cv}_{F} \quad \Longrightarrow \quad m\ddot{z} + c\dot{z} + kz = f$$ となります．ただし，$z$：位置，$v = \dot{z}$：速度，$a = \dot{v} = \ddot{z}$：加速度です．
　一方で，運動エネルギー $K$，位置エネルギー $U$，散逸エネルギー $D$ はそれぞれ
$$K = \dfrac{1}{2}m{v}^{2} = \dfrac{1}{2}m\dot{z}{}^{2},\quad U = \dfrac{1}{2}k{z}^{2},\quad D = \dfrac{1}{2}c{v}^{2} = \dfrac{1}{2}c\dot{z}{}^{2}$$ となり，ラグランジアンは $$L = K - U = \dfrac{1}{2}m\dot{z}{}^{2} - \dfrac{1}{2}k{z}^{2}$$ となります．ここで，一般化座標を $q = z$，一般化力を $Q = f$ とします．このとき，
$$\dfrac{{\rm{d}}}{{\rm{d}}t}\biggl(\frac{{\partial}L}{{\partial}\dot{z}}\biggr) = m\ddot{z},\quad \frac{{\partial}L}{{\partial}z} = -kz,\quad \frac{{\partial}D}{{\partial}\dot{z}} = c\dot{z}$$ ですので，ラグランジュの運動方程式は $$\dfrac{{\rm{d}}}{{\rm{d}}t}\biggl(\frac{\partial{L}}{\partial\dot{z}}\biggr) - \frac{\partial{L}}{\partial{z}} + \frac{\partial{D}}{\partial\dot{z}} = f \quad \Longrightarrow \quad m\ddot{z} + c\dot{z} + kz = f$$ となり，確かに，ニュートンの運動方程式により得られた結果と一致します．

2.2　回転型倒立振子の運動方程式の導出

　ここでは，ラグランジュ法により図 $1$ に示す回転型倒立振子の運動方程式を導出する手順を説明します．


図 $1$　回転型倒立振子

2.2.1　回転型倒立振子のパラメータ

　回転型倒立振子のパラメータを図 $2$ および表に示します．


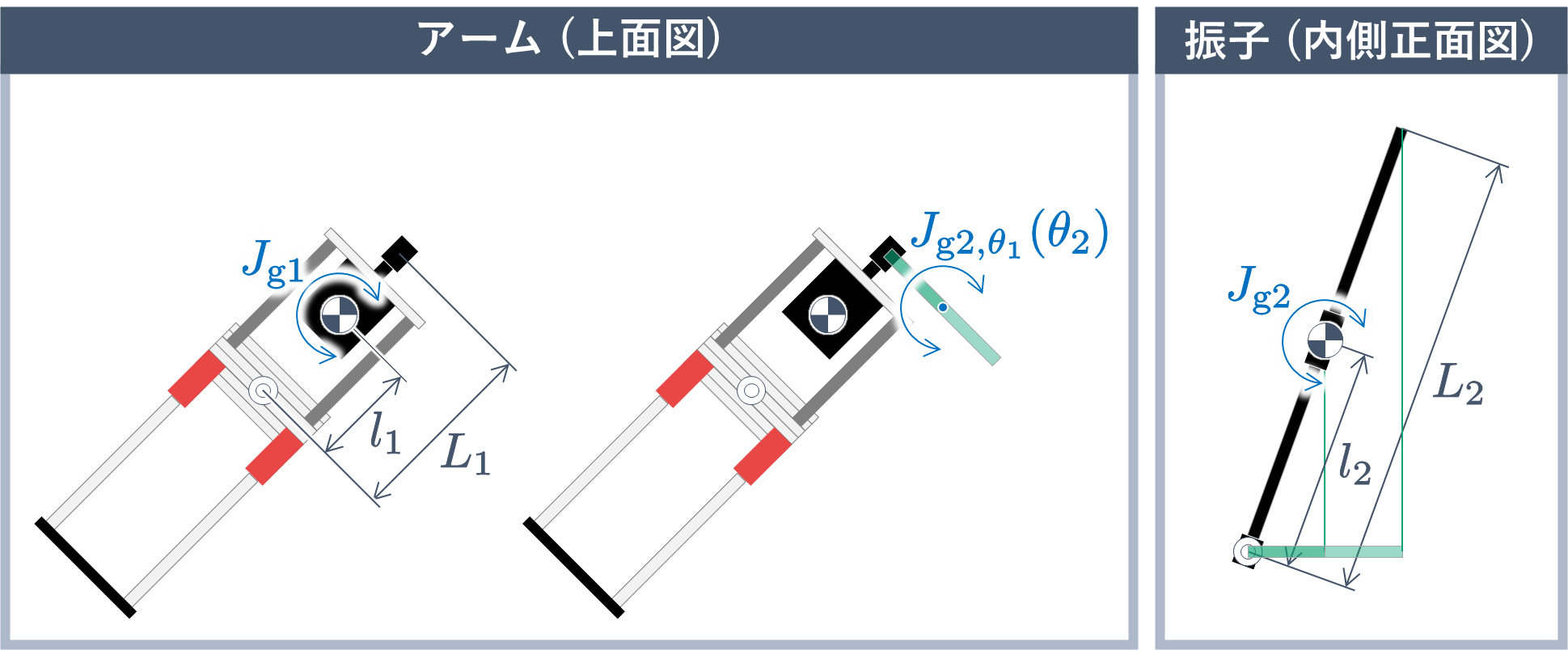図 $2$　回転型倒立振子のパラメータ

記号	説明
$g$ $\rm[m/s^2]$	重力加速度
$m_1$ $\rm[kg]$	アームの質量
$l_1$ $\rm[m]$	アームの軸から重心までの長さ
$L_1$ $\rm[m]$	アームの軸から振子の接合部までの長さ
$J_{\rm{g1}}$ $\rm[kg\cdot{m}^2]$	アームの重心まわりの慣性モーメント：$\theta_1$ 方向
$m_2$ $\rm[kg]$	振子の質量
$l_2$ $\rm[m]$	振子の軸から重心までの長さ
$L_2$ $\rm[m]$	振子の軸から先端までの長さ
$J_{\rm{g2}}$ $\rm[kg\cdot{m}^2]$	振子の重心まわりの慣性モーメント：$\theta_2$ 方向
$J_{{\rm{g2}},\theta_1}(\theta_2)$ $\rm[kg\cdot{m}^2]$	振子の重心まわりの慣性モーメント：$\theta_1$ 方向

2.2.2　回転型倒立振子の一般化座標と一般化力


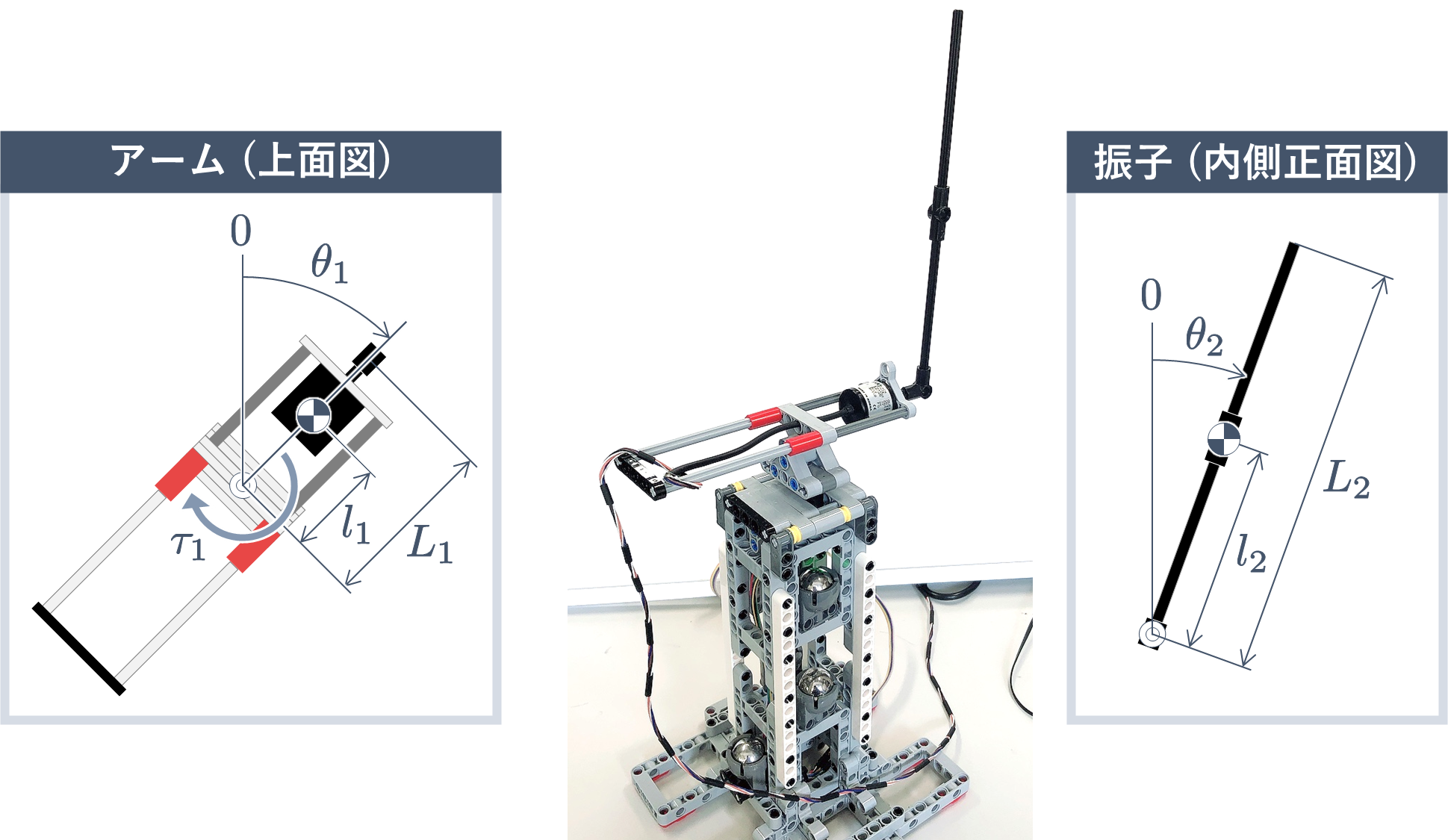図 $3$　回転型倒立振子の角度 $\theta_1$, $\theta_2$ $\rm[rad]$ とトルク $\tau_1$ $\rm[N{\cdot}m]$

　回転型倒立振子の場合，アームと振子という 2 つの質点で構成されており，図 $3$ に示すように，一般化座標，一般化力はそれぞれ

\begin{align}
	\pmb{q} = \begin{bmatrix}
			q_1 \\
			q_2
		\end{bmatrix}
	= \begin{bmatrix}
			\theta_1 \\
			\theta_2
		\end{bmatrix},\quad
	\pmb{Q} = \begin{bmatrix}
			Q_1 \\
			Q_2
		\end{bmatrix}
	= \begin{bmatrix}
			\tau_1 \\
			0
		\end{bmatrix}
	\tag{2}
\end{align}

となります．

2.2.3　アームと振子の重心座標


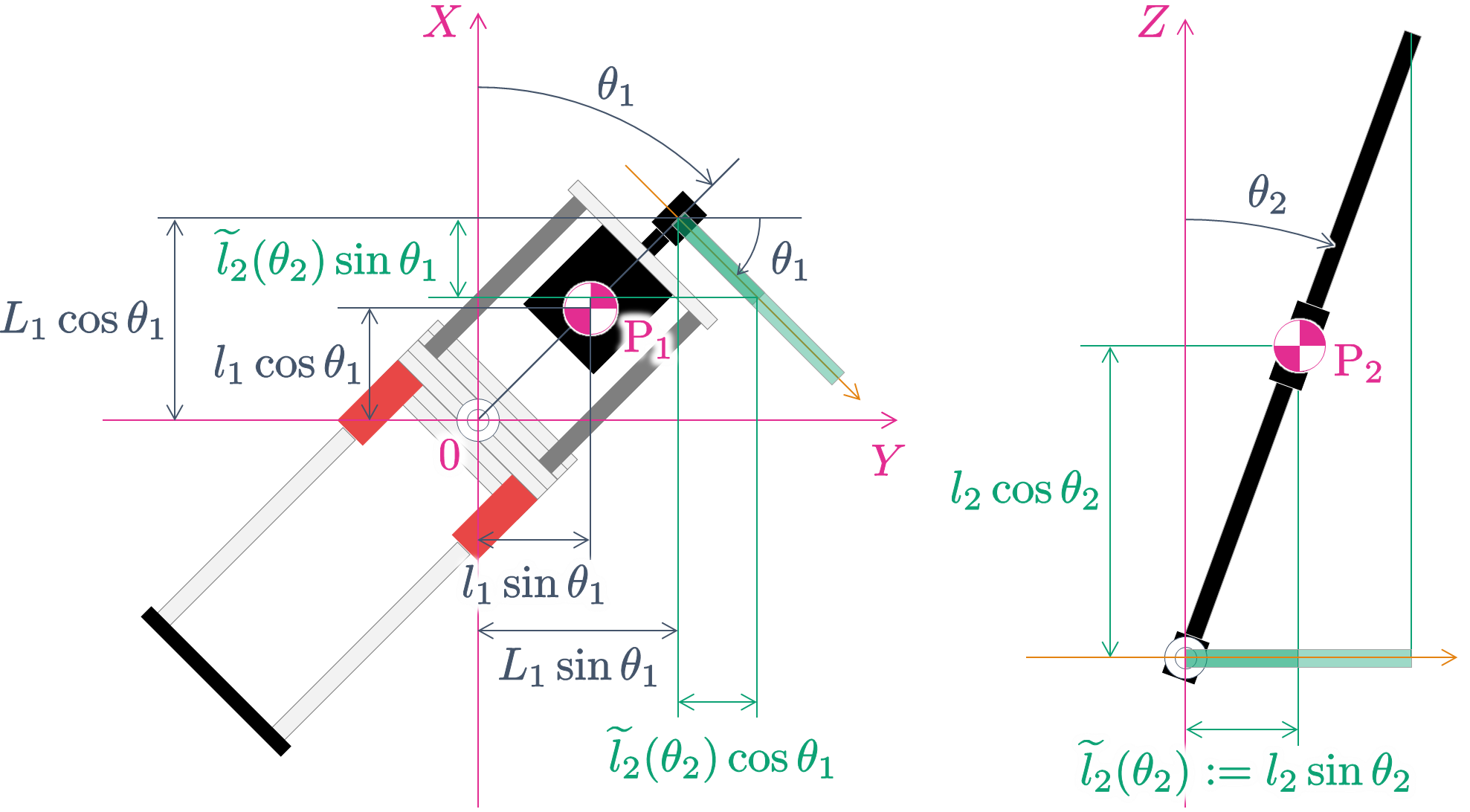図 $4$　回転型倒立振子の重心座標

　図 $4$ より，アームの重心を直交座標系 ${\rm P}_1\ (X_1,\ Y_1,\ Z_1)$ で表すと，

\begin{align}
	\left\{\begin{array}{rcl}
		{X}_{1} \hspace{-0.3cm}&=&\hspace{-0.3cm} {l}_{1}\cos{\theta}_{1} \\
		{Y}_{1} \hspace{-0.3cm}&=&\hspace{-0.3cm} {l}_{1}\sin{\theta}_{1} \\
		{Z}_{1} \hspace{-0.3cm}&=&\hspace{-0.3cm} 0
	\end{array}\right.
	\tag{3}
\end{align}

となります．同様に，図 $4$ より，$\widetilde{l}_{2}(\theta_2) := l_2\sin\theta_2$ であることを考慮して，振子の重心を直交座標系 ${\rm P}_2\ (X_2,\ Y_2,\ Z_2)$ で表すと，

\begin{align}
	\left\{\begin{array}{rcl}
		{X}_{2} \hspace{-0.3cm}&=&\hspace{-0.3cm} 
				{L}_{1}\cos{\theta}_{1} 
							- \widetilde{l}_{2}(\theta_2)\sin{\theta}_{1} \\
				\hspace{-0.3cm}&=&\hspace{-0.3cm} 
				{L}_{1}\cos{\theta}_{1} 
							- {l}_{2}\sin{\theta}_{2}\cdot\sin{\theta}_{1}\\
				\hspace{-0.3cm}&=&\hspace{-0.3cm} 
				{L}_{1}\cos{\theta}_{1} 
							- {l}_{2}\sin{\theta}_{1}\sin{\theta}_{2}\\
		{Y}_{2} \hspace{-0.3cm}&=&\hspace{-0.3cm} 
				{L}_{1}\sin{\theta}_{1} 
							+ \widetilde{l}_{2}(\theta_2)\cos{\theta}_{1} \\
				\hspace{-0.3cm}&=&\hspace{-0.3cm} 
				{L}_{1}\sin{\theta}_{1} 
							+ {l}_{2}\sin{\theta}_{2}\cdot\cos{\theta}_{1}\\
				\hspace{-0.3cm}&=&\hspace{-0.3cm} 
				{L}_{1}\sin{\theta}_{1} 
							+ {l}_{2}\cos{\theta}_{1}\sin{\theta}_{2}\\
		{Z}_{2} \hspace{-0.3cm}&=&\hspace{-0.3cm} 
				{l}_{2}\cos{\theta}_{2}
	\end{array}\right.
	\tag{4}
\end{align}

となります．

2.2.4　アームのエネルギー

【運動エネルギー】

　アームの重心は $X_1$, $Y_1$, $Z_1$ 方向の並進運動と $\theta_1$ 方向の回転運動をしているので，運動エネルギー $K_1$ は

\begin{align}
	{K}_{1} = \underbrace{\frac{1}{2}{m}_{1}(\dot{X}{}_{1}^{2} 
						       + \dot{Y}{}_{1}^{2} 
							   + \dot{Z}{}_{1}^{2})}_{並進運動}
			+ \underbrace{\dfrac{1}{2}{J}_{\rm{g1}}\dot{\theta}{}_{1}^{2}}_{{\theta_1\ 方向の回転運動}}
	\tag{5}
\end{align}

により求まります．したがって，$(3)$ 式を時間微分したものを $(5)$ 式に代入すると，

\begin{align}
	{K}_{1} = \frac{1}{2}{J}_{1}\dot{\theta}{}_{1}^{2}
	\quad ({J}_{1} = {J}_{\rm g1} + {m}_{1}{l}_{1}^{2})
	\tag{6}
\end{align}

が得られます．

【位置エネルギー】

　$(3)$ 式よりアームの位置エネルギー $U_1$ は，

\begin{align}
	{U}_{1} = {m}_{1}g{Z}_{1} = 0
	\tag{7}
\end{align}

となります．

【散逸エネルギー】

　アームの摩擦として，$\theta_1$ 方向の粘性摩擦を考慮します．このとき，アームの散逸エネルギー $D_1$ は，

\begin{align}
	{D}_{1} = \dfrac{1}{2}{c}_{1}\dot{\theta}{}_{1}^{2}
	\tag{8}
\end{align}

となります．ここで，${c}_{1}$ は粘性摩擦係数です．

2.2.5　振子のエネルギー

【運動エネルギー】

　振子の重心は $X_2$, $Y_2$, $Z_2$ 方向の並進運動と $\theta_2$ 方向の回転運動だけでなく，$\theta_1$ 方向の回転運動をしているので，運動エネルギー $K_2$ は，

\begin{align}
	{K}_{2} = \underbrace{\frac{1}{2}{m}_{1}(\dot{X}{}_{2}^{2} 
						       + \dot{Y}{}_{2}^{2} 
							   + \dot{Z}{}_{2}^{2})}_{並進運動}
			+ \underbrace{\dfrac{1}{2}{J}_{\rm{g2}}\dot{\theta}{}_{2}^{2}}_{{\theta_2\ 方向の回転運動}}
			+ \underbrace{\dfrac{1}{2}{J}_{\rm{g2},\theta_1}(\theta_2)\dot{\theta}{}_{1}^{2}}_{{\theta_1\ 方向の回転運動}}
	\tag{9}
\end{align}

により求まります．ただし，$\theta_1$ 方向の慣性モーメント ${J}_{\rm{g2},\theta_1}(\theta_2)$ は，付録の $\rm{(A.6)}$ 式で説明するように，

\begin{align}
	{J}_{\rm{g2},\theta_1}(\theta_2) = {J}_{\rm{g2}}\sin^2{\theta}_{2}
	\tag{10}
\end{align}

です．したがって，$(4)$ 式を時間微分したものを $(9)$ 式に代入すると，

\begin{align}
	{K}_{2} 
	&= \frac{1}{2}\bigl(
		{J}_{2} - {J}_{2}\cos^2{\theta}_{2} + {m}_{2}{L}_{1}^{2}
	\bigr)\dot{\theta}{}_{1}^{2}
	+ \frac{1}{2}{J}_{2}\dot{\theta}{}_{2}^{2}
	+ {m}_{2}{L}_{1}{l}_{2}\dot{\theta}_{1}\dot{\theta}_{2}\cos{\theta}_{2}
	\\
	&= \frac{1}{2}\bigl(
		{J}_{2}\sin^2{\theta}_{2} + {m}_{2}{L}_{1}^{2}
	\bigr)\dot{\theta}{}_{1}^{2}
	+ \frac{1}{2}{J}_{2}\dot{\theta}{}_{2}^{2}
	\\
	&\quad\quad\quad\quad
	+ {m}_{2}{L}_{1}{l}_{2}\dot{\theta}_{1}\dot{\theta}_{2}\cos{\theta}_{2}
	\quad ({J}_{2} = {J}_{\rm g2} + {m}_{2}{l}_{2}^{2})
	\tag{11}
\end{align}

が得られます．

【位置エネルギー】

　$(4)$ 式より振子の位置エネルギー $U_2$ は，

\begin{align}
	{U}_{2} = {m}_{2}g{Z}_{2} = {m}_{2}g{l}_{2}\cos{\theta}_{2}
	\tag{12}
\end{align}

となります．

【散逸エネルギー】

　
　振子の摩擦として，$\theta_2$ 方向の粘性摩擦を考慮します．このとき，振子の散逸エネルギー $D_1$ は，

\begin{align}
	{D}_{2} = \dfrac{1}{2}{c}_{2}\dot{\theta}{}_{2}^{2}
	\tag{13}
\end{align}

となります．ここで，${c}_{2}$ は粘性摩擦係数です．

2.2.6　回転型倒立振子の運動方程式

【運動エネルギー】

　全体の運動エネルギー $K$ は，$(6)$, $(11)$ 式より

\begin{align}
	K &= {K}_{1} + {K}_{2}
	\\
	&=
	\frac{1}{2}\bigl(
		{J}_{1} + {J}_{2}\sin^2{\theta}_{2} + {m}_{2}{L}_{1}^{2}
	\bigr)\dot{\theta}{}_{1}^{2}
	+ \frac{1}{2}{J}_{2}\dot{\theta}{}_{2}^{2}
	+ {m}_{2}{L}_{1}{l}_{2}\dot{\theta}_{1}\dot{\theta}_{2}\cos{\theta}_{2}
	\tag{14}
\end{align}

のように求まります．

【位置エネルギー】

　全体の運動エネルギー $U$ は，$(7)$, $(12)$ 式より

\begin{align}
	U = {U}_{1} + {U}_{2}
	  = {m}_{2}g{l}_{2}\cos{\theta}_{2}
	\tag{15}
\end{align}

のように求まります．

【散逸エネルギー】

　全体の運動エネルギー $D$ は，$(8)$, $(13)$ 式より

\begin{align}
	D = {D}_{1} + {D}_{2}
	= \dfrac{1}{2}{c}_{1}\dot{\theta}{}_{1}^{2}
	 + \dfrac{1}{2}{c}_{2}\dot{\theta}{}_{2}^{2}
	\tag{16}
\end{align}

のように求まります．

【ラグランジアン】

　ラグランジアン $L$ は，$(14)$, $(15)$ 式より

\begin{align}
	L &= K - U
	\\
	&=
	\frac{1}{2}\bigl(
		{J}_{1} + {J}_{2}\sin^2{\theta}_{2} + {m}_{2}{L}_{1}^{2}
	\bigr)\dot{\theta}{}_{1}^{2}
	+ \frac{1}{2}{J}_{2}\dot{\theta}{}_{2}^{2}
	\\
	&\quad\quad\quad\quad
	+ {m}_{2}{L}_{1}{l}_{2}\dot{\theta}_{1}\dot{\theta}_{2}\cos{\theta}_{2}
	- {m}_{2}g{l}_{2}\cos{\theta}_{2}
	\tag{17}
\end{align}

のように求まります．

【運動方程式】

　$(1)$ 式に示したラグランジュの運動方程式を，回転型倒立振子の場合にあてはめると，

\begin{align}
	\dfrac{{\rm{d}}}{{\rm{d}}t}\biggl(
		\frac{\partial{L}}{\partial\dot{\theta}_{1}}
	\biggr)
	- \frac{\partial{L}}{\partial{\theta}_{1}}
	+ \frac{\partial{D}}{\partial\dot{\theta}_{1}}
	&= {\tau}_{1}
	\tag{18}\\
	\dfrac{{\rm{d}}}{{\rm{d}}t}\biggl(
		\frac{\partial{L}}{\partial\dot{\theta}_{2}}
	\biggr)
	- \frac{\partial{L}}{\partial{\theta}_{2}}
	+ \frac{\partial{D}}{\partial\dot{\theta}_{2}}
	&= 0
	\tag{19}
\end{align}

となります．$(17)$, $(16)$ 式を $(18)$ 式の各項に代入すると，

\begin{align}
	\frac{\partial{L}}{\partial\dot{\theta}_{1}}
	&= \bigl({J}_{1}
			+ {J}_{2}\sin^{2}{\theta}_{2}
			+ {m}_{2}{L}_{1}^{2}\bigr)\dot{\theta}_{1}
	+ {m}_{2}{L}_{1}{l}_{2}\dot{\theta}_{2}\cos{\theta}_{2}
	\\
	\dfrac{{\rm{d}}}{{\rm{d}}t}\biggl(
		\frac{\partial{L}}{\partial\dot{\theta}_{1}}
	\biggr)
	&= \bigl({J}_{1} + {J}_{2}\sin^2{\theta}_{2} + {m}_{2}{L}_{1}^{2}\bigr)\ddot{\theta}_{1}
	+ {m}_{2}{L}_{1}{l}_{2}\cos{\theta}_{2}\cdot\ddot{\theta}_{2}
	\\
	&\quad
	+ (2{J}_{2}\dot{\theta}_{1}\cos{\theta}_{2}\sin{\theta}_{2} 
		- {m}_{2}{L}_{1}{l}_{2}\dot{\theta}_{2}\sin{\theta}_{2}\bigr)\dot{\theta}_{2}
	\\
	\frac{\partial{L}}{\partial{\theta}_{1}}
	&= 0
	\\
	\frac{\partial{D}}{\partial\dot{\theta}_{1}}
	&= {c}_{1}\dot{\theta}_{1}
\end{align}

となり，$(17)$, $(16)$ 式を $(19)$ 式の各項に代入すると，

\begin{align}
	\frac{\partial{L}}{\partial\dot{\theta}_{2}}
	&= {J}_{2}\dot{\theta}_{2} + {m}_{2}{L}_{1}{l}_{2}\dot{\theta}_{1}\cos{\theta}_{2}
	\\
	\dfrac{{\rm{d}}}{{\rm{d}}t}\biggl(
		\frac{\partial{L}}{\partial\dot{\theta}_{2}}
	\biggr)
	&= {J}_{2}\ddot{\theta}_{2} 
	+ {m}_{2}{L}_{1}{l}_{2}\cos{\theta}_{2}\cdot\ddot{\theta}_{1} 
	- {m}_{2}{L}_{1}{l}_{2}\dot{\theta}_{1}\dot{\theta}_{2}\sin{\theta}_{2}
	\\
	\frac{\partial{L}}{\partial{\theta}_{2}}
	&= {J}_{2}\dot{\theta}{}_{1}^{2}\cos{\theta}_{2}\sin{\theta}_{2}
		- {m}_{2}{L}_{1}{l}_{2}\dot{\theta}_{1}\dot{\theta}_{2}\sin{\theta}_{2}
		+ {m}_{2}g{l}_{2}\sin{\theta}_{2}
	\\
	\frac{\partial{D}}{\partial\dot{\theta}_{2}}
	&= {c}_{2}\dot{\theta}_{2}
\end{align}

となります．したがって，回転型倒立振子の運動方程式が

\begin{align}
	&
	\bigl({J}_{1}
		+ {m}_{2}{L}_{1}^{2}
		+ {J}_{2}\sin^{2}{\theta}_{2}\bigr)\ddot{\theta}_{1}
	+ {m}_{2}{L}_{1}{l}_{2}\cos{\theta}_{2}\cdot\ddot{\theta}_{2}
	\\
	&\qquad
	= {\tau}_{1} 
	- 2{J}_{2}\dot{\theta}_{1}\dot{\theta}_{2}\sin{\theta}_{\color{red}{2}}\cos{\theta}_{\color{red}{2}}
		+ {m}_{2}{L}_{1}{l}_{2}\dot{\theta}{}_{\color{red}{2}}^{2}\sin{\theta}_{\color{red}{2}}
		- {c}_{1}\dot{\theta}_{1}
	\tag{20}
	% --------
	\\
	&{m}_{2}{L}_{1}{l}_{2}\cos{\theta}_{2}\cdot\ddot{\theta}_{1}
		+ {J}_{2}\ddot{\theta}_{2}
	\\
	&\qquad
	= {J}_{2}\dot{\theta}{}_{1}^{2}\sin{\theta}_{2}\cos{\theta}_{2}
		+ {m}_{2}g{l}_{2}\sin{\theta}_{2}
		- {c}_{2}\dot{\theta}_{2}
	\tag{21}
\end{align}

のように得られます．

3. MATLAB / Symbolic Math Toolbox の利用

　MATLAB / Symbolic Math Toolbox（MathWorks 社）を利用すると，ラグランジュ法を実装することができ，手計算の手間を減らすことができます．

　Symbolic Math Toolbox は，Mathematica（Wolfram Research 社）や Maple（Maplesoft 社）のように，数式処理（文字式の計算）を行うことができる MATLAB 用のツールボックスです．たとえば，

\begin{align}
	f(x) = x^2 + 2x + 3
\end{align}

の微積分は以下のようにして操作します．

Symbolic Math Toolbox の使用例

>> syms x real                    % 実数 x をシンボリック変数として定義
>> f(x) = x^2 + 2*x + 3           % f(x) の定義
f(x) =
x^2 + 2*x + 3
>> f(4)                           % f(4) の計算
ans =
27
>> df(x) = diff(f(x),x)           % f(x) を x で微分
df(x) =
2*x + 2
>> int_f(x) = int(f(x),x)         % f(x) を x で積分（不定積分）
int_f(x) =
(x*(x^2 + 3*x + 9))/3
>> def_int_f = int(f(x),x,-2,4)   % f(x) を x で積分（区間 [-2,4] の定積分）
def_int_f =
54

　まず，Symbolic Math Toolbox を利用してラグランジュ法を実装する際の注意点について説明します．

　重心座標の成分 $X_1$, $Y_1$, $Z_1$, $X_2$, $Y_2$, $Z_2$ は，$(3)$, $(4)$ 式に示すように，一般化座標 $q_1 = \theta_1$, $q_2 = \theta_2$ に依存するので，たとえば，

\begin{align}
	{X}_{2}({q}_{1},{q}_{2}) 
	&= {L}_{1}\cos{q}_{1} 
	 - {l}_{2}\sin{q}_{1}\sin{q}_{2}
	\\
	&= {L}_{1}\cos{\theta}_{1} 
	 - {l}_{2}\sin{\theta}_{1}\sin{\theta}_{2}
\end{align}

の時間微分は，

\begin{align}
	\dot{X}_{2}
	= \frac{{\rm d}{X}_{2}}{{\rm d}t}
	&= \frac{{\partial}{X}_{2}}{{\partial}{q}_{1}}\frac{{\rm d}{q}_{1}}{{\rm d}t}
	+ \frac{{\partial}{X}_{2}}{{\partial}{q}_{2}}\frac{{\rm d}{q}_{2}}{{\rm d}t}
	\\
	&= \frac{{\partial}{X}_{2}}{{\partial}{\theta}_{1}}\frac{{\rm d}{\theta}_{1}}{{\rm d}t}
	+ \frac{{\partial}{X}_{2}}{{\partial}{\theta}_{2}}\frac{{\rm d}{\theta}_{2}}{{\rm d}t}
	\\
	&= \frac{{\partial}{X}_{2}}{{\partial}{\theta}_{1}}\dot{\theta}_{1}
	+ \frac{{\partial}{X}_{2}}{{\partial}{\theta}_{2}}\dot{\theta}_{2}
\end{align}

のように書き換えることができます．この式に基づいて，$X_2$ の時間微分を求めると，

\begin{align}
	\frac{{\partial}{X}_{2}}{{\partial}{\theta}_{1}}
	&= {}- {L}_{1}\sin{\theta}_{1} 
			- {l}_{2}\cos{\theta}_{1}\sin{\theta}_{2}
	\\
	\frac{{\partial}{X}_{2}}{{\partial}{\theta}_{2}} 
	&= {}- {l}_{2}\sin{\theta}_{1}\cos{\theta}_{2}
\end{align}

より

\begin{align}
	\dot{X}_{2}
	&= \frac{{\partial}{X}_{2}}{{\partial}{\theta}_{1}}\dot{\theta}_{1}
	+ \frac{{\partial}{X}_{2}}{{\partial}{\theta}_{2}}\dot{\theta}_{2}
	\\
	&= \bigl({}- {L}_{1}\sin{\theta}_{1} 
			 - {l}_{2}\cos{\theta}_{1}\sin{\theta}_{2} \bigr)\dot{\theta}_{1}
	- {l}_{2}\sin{\theta}_{1}\cos{\theta}_{2} \cdot\dot{\theta}_{2}
	\\
	&= {}- \dot{\theta}_{1}\bigl({L}_{1}\sin{\theta}_{1} 
			+ {l}_{2}\cos{\theta}_{1}\sin{\theta}_{2}\bigr)
	- {l}_{2}\hskip2pt\dot{\theta}_{2}\sin{\theta}_{1}\cos{\theta}_{2}
\end{align}

となります．この結果は，直接的に時間微分を求めた結果

\begin{align}
	\dot{X}_{2} &= {L}_{1}(\cos{\theta}_{1})^\prime 
				- {l}_{2}\bigl\{
							(\sin{\theta}_{1})^\prime \sin{\theta}_{2}
						    + \sin{\theta}_{1}\cdot(\sin{\theta}_{2})^\prime
						\bigr\}
	\\
	&= {L}_{1}({}-\dot{\theta}_{1}\sin{\theta}_{1}) 
				- {l}_{2}\bigl\{
							(\dot{\theta}_{1}\cos{\theta}_{1}) \cdot\sin{\theta}_{2}
						   + \sin{\theta}_{1}\cdot (\dot{\theta}_{2}\cos{\theta}_{2})
						\bigr\}
	\\
	&= - \dot{\theta}_{1}\bigl({L}_{1}\sin{\theta}_{1} 
			+ {l}_{2}\cos{\theta}_{1}\sin{\theta}_{2}\bigr)
	- {l}_{2}\hskip2pt\dot{\theta}_{2}\sin{\theta}_{1}\cos{\theta}_{2}
\end{align}

と一致します．

後述の M ファイル " lagrange_rotary_ip.m " において，dX1, dY1, dZ1, dX2, dY2, dZ2 の計算に利用されています．

　同様に，$\partial{L}/\partial{\dot{q}_{i}}$ は一般化座標 $q_1 = \theta_1$, $q_2 = \theta_2$ およびその時間微分 $\dot{q}_1 = \dot{\theta}_1$, $\dot{q}_2 = \dot{\theta}_2$ に依存するので，　

\begin{align}
	{M}_{i}({q}_{1},{q}_{2},\dot{q}_{1},\dot{q}_{2})
	&:= \dfrac{\partial{L}}{\partial\dot{q}_{i}}
\end{align}

とおくと，　

\begin{align}
	\dfrac{{\rm{d}}}{{\rm{d}}t}\biggl(
		\frac{\partial{L}}{\partial\dot{q}_{i}}
	\biggr)
	= \dot{M}_{i}
	&= \frac{{\partial}{M}_{i}}{{\partial}{q}_{1}}\frac{{\rm d}{q}_{1}}{{\rm d}t}
	+ \frac{{\partial}{M}_{i}}{{\partial}{q}_{2}}\frac{{\rm d}{q}_{2}}{{\rm d}t}
	+ \frac{{\partial}{M}_{i}}{{\partial}\dot{q}_{1}}\frac{{\rm d}\dot{q}_{1}}{{\rm d}t}
	+ \frac{{\partial}{M}_{i}}{{\partial}\dot{q}_{2}}\frac{{\rm d}\dot{q}_{2}}{{\rm d}t}
	\\
	&= \frac{{\partial}{M}_{i}}{{\partial}{q}_{1}}\dot{q}_{1}
	 + \frac{{\partial}{M}_{i}}{{\partial}{q}_{2}}\dot{q}_{2}
	 + \frac{{\partial}{M}_{i}}{{\partial}\dot{q}_{1}}\ddot{q}_{1}
	 + \frac{{\partial}{M}_{i}}{{\partial}\dot{q}_{2}}\ddot{q}_{2}
	\\
	&= \frac{{\partial}{M}_{i}}{{\partial}{\theta}_{1}}\dot{\theta}_{1}
	 + \frac{{\partial}{M}_{i}}{{\partial}{\theta}_{2}}\dot{\theta}_{2}
	 + \frac{{\partial}{M}_{i}}{{\partial}\dot{\theta}_{1}}\ddot{\theta}_{1}
	 + \frac{{\partial}{M}_{i}}{{\partial}\dot{\theta}_{2}}\ddot{\theta}_{2}
\end{align}

により計算できます．

後述の M ファイル " lagrange_rotary_ip.m " において，ddLq(i) の計算に利用されています．

　このことに注意して，ラグランジュ法を実装した M ファイルと実行結果を以下に示します．

M ファイル "lagrange_rotary_ip.m"

clear
format compact

syms m1 m2 real
syms c1 c2 real
syms Jg1 Jg2 J1 J2 real
syms l1 L1 l2 g real
syms th1 th2 dth1 dth2 ddth1 ddth2 tau1 real

q   = [   th1    th2 ]';
dq  = [  dth1   dth2 ]';
ddq = [ ddth1  ddth2 ]';
f   = [  tau1     0  ]';

% ****************************************
% --- アームの重心座標 P1 (X1,Y1,Z1)
X1 = l1*cos(th1);
Y1 = l1*sin(th1);
Z1 = 0;

% --- 時間微分 d(X1)/dt, d(Y1)/dt, d(Z1)/dt
dX1 = diff(X1,q(1))*dq(1) ...
    + diff(X1,q(2))*dq(2);
dY1 = diff(Y1,q(1))*dq(1) ...
    + diff(Y1,q(2))*dq(2);
dZ1 = diff(Z1,q(1))*dq(1) ...
    + diff(Z1,q(2))*dq(2);

% --- アームの運動エネルギー
K1 = (1/2)*m1*(dX1^2 + dY1^2 + dZ1^2) ...
   + (1/2)*Jg1*dth1^2;
K1 = simplify(subs(K1,Jg1,J1-m1*l1^2));

% --- アームの位置エネルギー
U1 = 0;

% --- アームの散逸エネルギー
D1 = (1/2)*c1*dth1^2;

% ****************************************
% --- 振子の重心座標 P2 (X2,Y2,Z2)
X2 = L1*cos(th1) - l2*sin(th1)*sin(th2);
Y2 = L1*sin(th1) + l2*cos(th1)*sin(th2);
Z2 =               l2*cos(th2);

% --- 時間微分 d(X2)/dt, d(Y2)/dt, d(Z2)/dt
dX2 = diff(X2,q(1))*dq(1) ...
    + diff(X2,q(2))*dq(2);
dY2 = diff(Y2,q(1))*dq(1) ...
    + diff(Y2,q(2))*dq(2);
dZ2 = diff(Z2,q(1))*dq(1) ...
    + diff(Z2,q(2))*dq(2);

Jg2th1 = Jg2*sin(th2)^2;

% --- 振子の運動エネルギー
K2 = (1/2)*m2*(dX2^2 + dY2^2 + dZ2^2) ...
   + (1/2)*Jg2*dth2^2 ...
   + (1/2)*Jg2th1*dth1^2;
K2 = simplify(subs(K2,Jg2,J2-m2*l2^2));

% --- アームの位置エネルギー
U2 = m2*g*Z2;

% --- アームの散逸エネルギー
D2 = (1/2)*c2*dth2^2;

% ****************************************
K = K1 + K2;
U = U1 + U2;
D = D1 + D2;

L = K - U;

% ****************************************
N = length(q);
for i = 1:N
    dLq(i) = diff(L,dq(i));

    temp = 0;
    for j = 1:N
        temp = temp + diff(dLq(i), q(j))* dq(j) ...
                    + diff(dLq(i),dq(j))*ddq(j);
    end
    ddLq(i) = temp;
  
    eq(i) = ddLq(i) - diff(L,q(i)) ...
          + diff(D,dq(i)) - f(i);
end

eq = simplify(eq')

M ファイル "lagrange_rotary_ip.m" の実行結果

>> lagrange_rotary_ip
eq =
 ddth1*(J1 + J2 + L1^2*m2 - J2*cos(th2)^2) - tau1 + c1*dth1 + dth2*(2*J2*dth1*cos(th2)*sin(th2) - L1*dth2*l2*m2*sin(th2)) + L1*ddth2*l2*m2*cos(th2)
                                                    - J2*cos(th2)*sin(th2)*dth1^2 + J2*ddth2 + c2*dth2 - g*l2*m2*sin(th2) + L1*ddth1*l2*m2*cos(th2)

ここで示した結果は，$(20)$, $(21)$ 式における一般化力を左辺に移項した結果と一致しています．ただし，実行結果の

J1 + J2 + L1^2*m2 - J2*cos(th2)^2

の部分を書き換えると，

J1 + L1^2*m2 + J2*sin(th2)^2

となることに注意してください．

1 - cos(th2)^2 を sin(th2)^2 に置き換える方法がわかりませんでした …

4. おわりに

　今回は，回転型倒立振子のモデリングの作業の第 1 段階として，ラグランジュの方法に基づいて「運動方程式」を求めました．次回は，モデリングの作業の第 2 段階として，「パラメータ同定」の方法について説明したいと思います．

（終わり）

参考文献

杉江俊治, 岡田昌史：並列倒立振子システムの H∞ 制御，Vol.6, No.12, pp.543-551 (1993)
　$\cdots\cdots$ https://doi.org/10.5687/iscie.6.543
B. S. Cazzolato, and Z. Prime: On the Dynamics of the Furuta Pendulum, Journal of Control Science and Engineering, Vol.2011, 8 pages (2011)
　$\cdots\cdots$ https://doi.org/10.1155/2011/528341
川田昌克：MATLAB/Simulink と実機で学ぶ制御工学 ― PID 制御から現代制御まで ―，TechShare (2013)
川田昌克：LEGO MINDSTORMS を利用した回転型倒立振子の開発，計測と制御，Vol.54，No.3，pp.192-195 (2015)
　$\cdots\cdots$ https://doi.org/10.11499/sicejl.54.192
川田昌克（編著），東　俊一，市原裕之，浦久保孝光，大塚敏之，甲斐健也，國松禎明，澤田賢治，永原正章，南　裕樹：倒立振子で学ぶ制御工学，森北出版 (2017.2.28)
$\Longrightarrow$ サポートページはこちら
川田昌克：物理法則に基づくモデリング（「初学者のための図解でわかる制御工学 I ― 基礎編 ―」特集号解説），システム/制御/情報，Vol.56，No.4，pp.166-169 (2012)
　$\cdots\cdots$ https://doi.org/10.11509/isciesci.56.4_166

付録：振子の慣性モーメント

　並進運動（直線的に動かす運動）では，質量が「物体の動かしにくさの度合い」となり，これを慣性と呼びます．一方，回転運動では，質量だけでなく長さも「物体の回転させにくさの度合い」となり，この度合いを表す物理量を慣性モーメントと呼びます．

　たとえば，図 $\rm A.1$ の右図に示すように，振子が質量 $m_2$ $\rm[kg]$，長さが $L_2 = 2l_2$ $\rm[m]$ の均質な棒（一様な棒）であるとします．このとき，重心は振子の中央となりますが，この重心まわりの慣性モーメント $J_{\rm{g2}}$ $\rm[kg{\cdot}m^2]$ は，

\begin{align}
	{J}_{\rm{g2}} = \int_{-{l}_{2}}^{{l}_{2}}{x}^{2}\rho\hspace{1pt}{\rm d}x
	\tag{A.1}
\end{align}

により計算できます．ただし，$\rho$ は振子の線密度であり，$\rho = m_2 / L_2 = m_2 / (2l_2)$ $\rm[kg/m]$ となります．したがって，

\begin{align}
	{J}_{\rm{g2}} &= \dfrac{{m}_{2}}{2{l}_{2}}\int_{-{l}_{2}}^{{l}_{2}}{x}^{2}{\rm d}x
	= \dfrac{{m}_{2}}{2{l}_{2}}\biggl[\dfrac{1}{3}{x}^{3}\biggr]_{-{l}_{2}}^{{l}_{2}}
	\\
	&= \dfrac{1}{3}{m}_{2}{l}_{2}^{2}
	\tag{A.2}
\end{align}

となります．同様に，振子の片端（振子の回転軸）まわりの慣性モーメント ${J}_{2}$ $\rm[kg{\cdot}m^2]$ は，

\begin{align}
	{J}_{2} = \int_{0}^{2{l}_{2}}{x}^{2}\rho\hspace{1pt}{\rm d}x
	\tag{A.3}
\end{align}

により計算できますので，

\begin{align}
	{J}_{2} &= \dfrac{{m}_{2}}{2{l}_{2}}\int_{0}^{2{l}_{2}}
						{x}^{2}{\rm d}x
	= \dfrac{{m}_{2}}{2{l}_{2}}\biggl[\dfrac{1}{3}{x}^{3}\biggr]_{0}^{2{l}_{2}}
	\\
	&= \dfrac{4}{3}{m}_{2}{l}_{2}^{2}
	\\
	&= {J}_{\rm{g2}} + {m}_{2}{l}_{2}^{2}
	\tag{A.4}
\end{align}

となります．$J_2$ と $J_{\rm{g2}}$ の関係式は，「平行軸の定理」と呼ばれます．


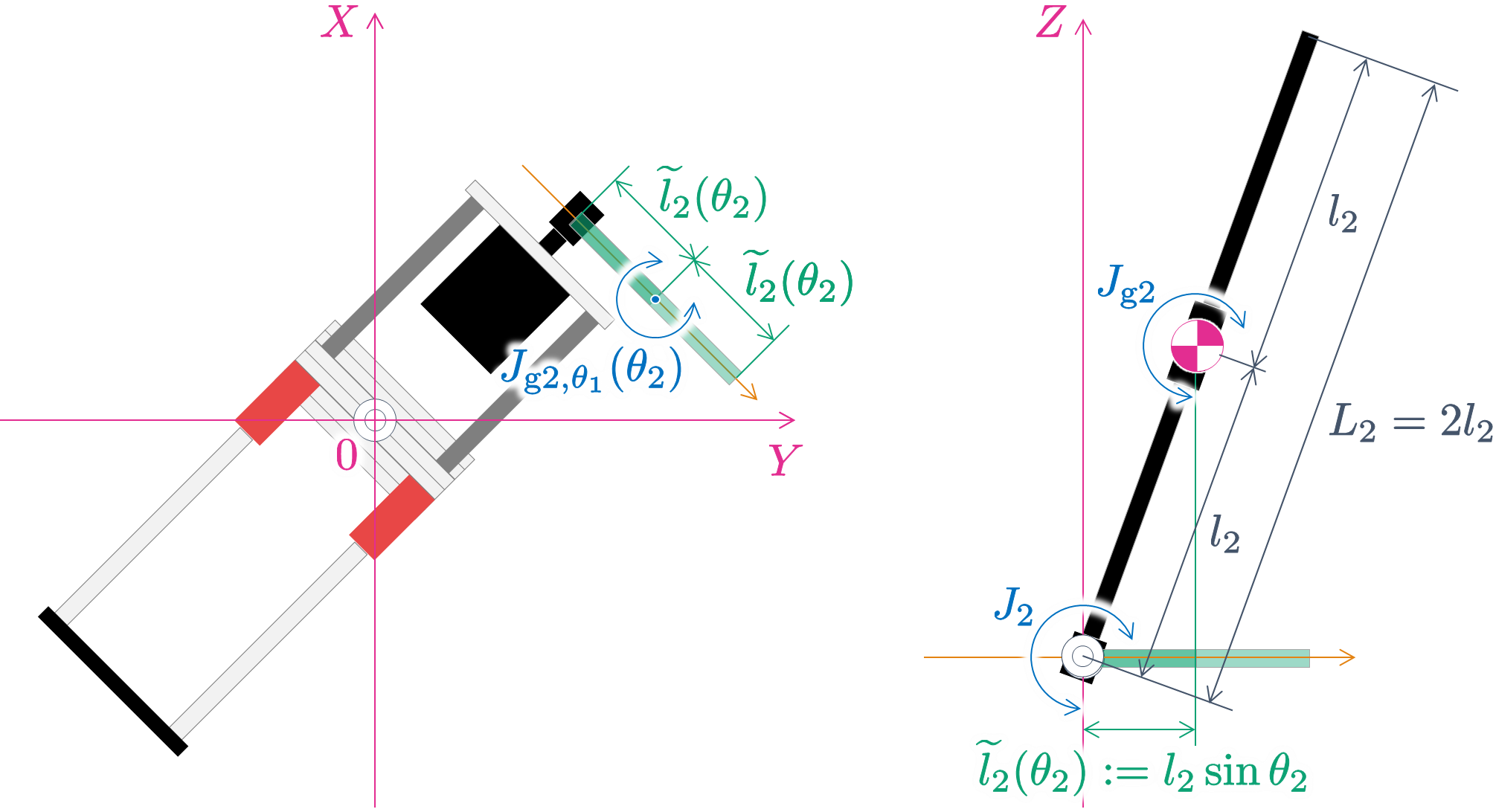図 $\rm A.1$　振子の慣性モーメント

　さて，回転型倒立振子の場合，アームの先端に取りつけられた振子は，$\theta_2$ 方向（振子の回転方向）だけでなく，$\theta_1$ 方向（アームの回転方向）にも回転しています．したがって，振子の慣性モーメントは $\theta_2$ 方向と $\theta_1$ 方向の 2 つを考慮する必要があります．$\theta_2$ 方向の慣性モーメントは上述で求めた $J_{\rm{g2}}$ ですので，ここでは，$\theta_1$ 方向の慣性モーメント $J_{{\rm{g2}},\theta_1}$ を求めます．

　振子が一様な棒であるとしたとき，$XY$ 平面での線密度 $\widetilde{\rho}(\theta_2)$ は

\begin{align}
	\widetilde{\rho}(\theta_2) 
	= \dfrac{{m}_{2}}{2\widetilde{l}_{2}({\theta}_{2})}
	= \dfrac{{m}_{2}}{2{l}_{2}\sin{\theta}_{2}}
	\tag{A.5}
\end{align}

です．したがって，振子の $XY$ 平面における重心まわりの慣性モーメント $J_{{\rm{g2}},\theta_1}(\theta_2)$ $\rm[kg{\cdot}m^2]$ は，

\begin{align}
	{J}_{{\rm{g2}},{\theta}_{1}}({\theta}_{2})
	&= \int_{-\widetilde{l}_{2}({\theta}_{2})}^{\widetilde{l}_{2}({\theta}_{2})}
		{x}^{2}\widetilde{\rho}({\theta}_{2})\hspace{1pt}{\rm d}x
	= \dfrac{{m}_{2}}{2{l}_{2}\sin{\theta}_{2}}
	\int_{-{l}_{2}\sin{\theta}_{2}}^{{l}_{2}\sin{\theta}_{2}}
		{x}^{2}{\rm d}x
	\\
	&= \dfrac{{m}_{2}}{2{l}_{2}\sin{\theta}_{2}}
		\biggl[\dfrac{1}{3}{x}^{3}\biggr]_{-{l}_{2}\sin{\theta}_{2}}^{{l}_{2}\sin{\theta}_{2}}
	= \dfrac{{m}_{2}}{2{l}_{2}\sin{\theta}_{2}}\dfrac{1}{3}
		\cdot 2{l}_{2}^{3}\sin^{3}{\theta}_{2}
	\\
	&= \dfrac{1}{3}{m}_{2}{l}_{2}^{2}\sin^{2}{\theta}_{2}
	\\
	&= {J}_{\rm{g2}}\sin^{2}{\theta}_{2}
	\tag{A.6}
\end{align}

のようになります．　

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

LEGO 部品を利用した回転型倒立振子のレシピを公開！（第 3 回：運動方程式 ー MATLAB / Symbolic Math Toolbox）

1. はじめに

2. ラグランジュ法による運動方程式の導出

2.1 ラグランジュ法とは？

2.2 回転型倒立振子の運動方程式の導出

2.2.1 回転型倒立振子のパラメータ

2.2.2 回転型倒立振子の一般化座標と一般化力

2.2.3 アームと振子の重心座標

2.2.4 アームのエネルギー

【運動エネルギー】

【位置エネルギー】

【散逸エネルギー】

2.2.5 振子のエネルギー

【運動エネルギー】

【位置エネルギー】

【散逸エネルギー】

2.2.6 回転型倒立振子の運動方程式

【運動エネルギー】

【位置エネルギー】

【散逸エネルギー】

【ラグランジアン】

【運動方程式】

3. MATLAB / Symbolic Math Toolbox の利用

4. おわりに

参考文献

付録：振子の慣性モーメント

LEGO 部品を利用した回転型倒立振子のレシピを公開！（第 3 回：運動方程式ー MATLAB / Symbolic Math Toolbox）

2.1　ラグランジュ法とは？

2.2　回転型倒立振子の運動方程式の導出

2.2.1　回転型倒立振子のパラメータ

2.2.2　回転型倒立振子の一般化座標と一般化力

2.2.3　アームと振子の重心座標

2.2.4　アームのエネルギー

2.2.5　振子のエネルギー

2.2.6　回転型倒立振子の運動方程式