LoginSignup
11
5
MATLAB/Simulink Advent Calendar 2022Advent Calendar 2022Day 25
@Carter

Simulink の分岐処理を利用して『回転型 LEGO 倒立振子』を振り上げ安定化！

Last updated at Posted at 2022-12-24

0. 配布ファイル

　本記事で利用した MATLAB 関連ファイルは github で公開していますので，ご自由にご利用ください！

配布ファイル

おまけで説明する非線形シミュレーションを行うファイル

も提供していますよ！

ちなみに，本記事の実機実験は，MinSeg 社の MinSegShield M2V5 Dual Axis Balancing Kit を利用した回転型 LEGO 倒立振子により行っています．詳しくは

をご参照ください．

注意
今回，配布する実機実験用の Simulink モデルは，Manually で COM Port 番号を 3 に設定していますので，必要に応じて番号を変更してください．また，MinSegMega Shield キット付属の Arduino 互換ボードの種類によっては，Automatically と設定しても大丈夫です．

とはいっても，多くの方は，この実機実験をする環境にはないと思いますが，非線形シミュレーションにより雰囲気だけでも感じ取ってください．

　なお，配布するファイル等の動作保証およびテクニカルサポート，発生した損害に対する責任は負いません．

1. はじめに

　何も考えずに

の最終日に登録してしまった…　だって，空席だったんで…　ただ単に，締切日を先延ばしにしたかっただけなんです．

　それはさておき，みなさん，『倒立振子』（「とうりつしんし」あるいは「とうりつふりこ」）って知ってますか？　『倒立振子』とは『ほうきを建てる遊び』を，『自動制御』の技術によりこのように実現したものです．
image.png

倒立振子の解説記事やスライドは

などをご参照ください．大御所の先生方の座談会の記事

なんかも面白いですよ．是非，ご一読ください．

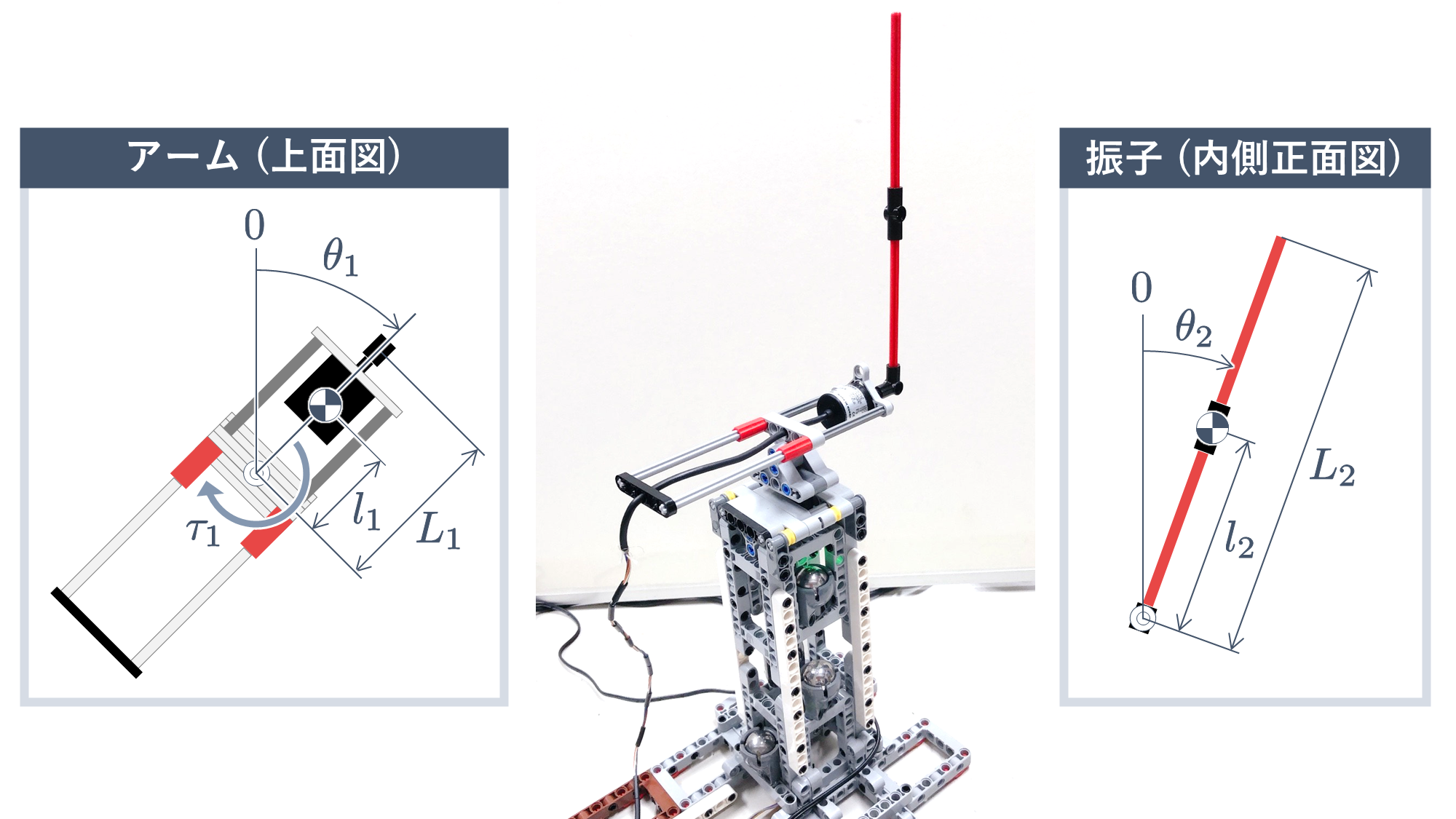
　さて，本記事では，LEGO 部品を利用して製作された『回転型倒立振子 (Furuta Pendulum)』

の振り上げ安定化制御を，MATLAB/Simulink により実現する方法を説明します．Segway を模範とした『車輪型倒立振子』

とは異なり，『回転型倒立振子』は振子がソンビのよう繰り返し立ち上がらせることができるので，展示会などで観客の皆さんを喜ばせるのに適しているのではないかと思います．まずは，この動画をご覧ください．

image.png
また，『回転型倒立振子』は標準的な『台車型倒立振子』

と比べてコンパクトな構造であるという利点もあります．

　ところで，マスワークス様から無償で提供されている Simulink Support Package for Arduino Hardware を利用することで，Simulink によりお手軽に Arduino にコントローラを実装して動かしたり，リアルタイムで信号の計測を行うことができるようになりました．なんとスバラシイことでしょう！ 　当然，情報工学科出身なのにプログラミング「よわよわ」な私は， Arduino を動かすのに，スケッチ (sketch) ではなく，Simulink を利用したくなりますよね．

　多くの場合，『回転型倒立振子』の振り上げ安定化制御を実現するために，

  • 振り上げコントローラ
  • 安定化コントローラ

を適当な振子の角度で切り替えます．振子の角度だけで 2 つのコントローラを切り替えるだけであれば，"Switch" っていう Simulink ブロックを利用すれば良いでしょうが，振子の角度だけでなく角速度も切り替え条件に利用したり，無制御の領域を考えたりすると，分岐処理が複雑になり，なかなか大変そうです．

　そこで，本記事では，この複雑な分岐処理を Simulink で実装するために，Simulink ブロック "If" および "If Action Subsystem" を利用します．なお，MATLAB/Simulink Advent Calendar の記事ですので，理論については付録 A にまとめてます！

　ちなみに，本記事のきっかけは toshi | Simulink の中の人さんのつぶやきです．
　情報提供，ありがとうございました！

2. 振り上げ安定化制御を実現するコントローラの実装

2.1　回転型倒立振子の非線形モデル

image.png

　この記事で説明したように，倒立振子の非線形モデルは

\begin{align}
	\require{color}
	\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
	\definecolor{myblue}{rgb}{0,0.4392,0.7529}
	\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
	\definecolor{mypink}{rgb}{1,0.4,0.6}
	\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
	\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
	% =================================================
	\ddot{\theta}_{1} 
	&={}- {\alpha}_{1}\dot{\theta}_{1} 
	+ {\beta}_{1}v 
	\tag{1}
	% --------
	\\
	{L}_{1}\cos{\theta}_{2}\cdot\ddot{\theta}_{1}
		+ {\alpha}_{2}\ddot{\theta}_{2}
	&= {\alpha}_{2}\dot{\theta}{}_{1}^{2}\sin{\theta}_{2}\cos{\theta}_{2}
		+ g\sin{\theta}_{2}
		- {\beta}_{2}\dot{\theta}_{2}
	\tag{2}
\end{align}

で与えられます．ただし，

\begin{align}
    {\alpha}_{2} = \dfrac{{J}_{2}}{{m}_{2}{l}_{2}},\ 
    {\beta}_{2} = \dfrac{{c}_{2}}{{m}_{2}{l}_{2}}
\end{align}

です．パラメータの値は以下のとおりです．

パラメータ 値　　　　　　　　　　　　　　 MATLAB 変数
$g$ $9.81 \times 10^{ 0}$ $[\rm{m/s^2}]$ g
$L_1$ $7.00 \times 10^{-2}$ $[\rm{m}]$ L1
$\alpha_1$ $1.53 \times 10^{ 1}$ a1
$\beta_1$ $7.06 \times 10^{ 1}$ b1
$\alpha_2$ $1.10 \times 10^{-1}$ a2
$\beta_2$ $3.59 \times 10^{-2}$ b2

2.2　切り替え条件

　振子の振り上げ安定化を行うために，本記事では，振子の角度や角速度に応じて

  • 振り上げ制御（導出は付録 A を参照）
\begin{align}
	\require{color}
	\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
	\definecolor{myblue}{rgb}{0,0.4392,0.7529}
	\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
	\definecolor{mypink}{rgb}{1,0.4,0.6}
	\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
	\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
	\definecolor{mydarkyellow}{rgb}{0.8941,0.5137,0.0706}
	% =================================================
    \textcolor{myblue}{v}\; &
    \textcolor{myblue}{= {f}_{\rm sw}(\dot{\theta}_{1},\,{\phi}_{2},\,\dot{\phi}_{2})}
    \\
    &\textcolor{myblue}{:= \dfrac{1}{{\beta}_{1}}\biggl(
            {\alpha}_{1}\dot{\theta}_{1}
            + {k}_{\rm sw}\dot{\phi}_{2}\cos{\phi}_{2}
            - \dfrac{{\alpha}_{2}}{{L}_{1}}
                \dot{\theta}{}_{1}^{2}\sin{\phi}_{2}
            + \dfrac{{\beta}_{2}}
                    {{L}_{1}}
              \dfrac{\dot{\phi}_{2}}
                    {\cos{\phi}_{2}}
        \biggr)}
    \tag{3}
\end{align}
  • 安定化制御
\begin{align}
    \textcolor{mygreen}{v}\; &\textcolor{mygreen}{= Kx}
    \\ 
      &\textcolor{mygreen}{
       = {k}_{1}{\theta}_{1}
       + {k}_{2}\dot{\theta}_{1}
       + {k}_{3}{\theta}_{2}
       + {k}_{4}\dot{\theta}_{2}}
    \tag{4}
\end{align}
  • 無制御
\begin{align}
	\require{color}
	\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
	\definecolor{myblue}{rgb}{0,0.4392,0.7529}
	\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
	\definecolor{mypink}{rgb}{1,0.4,0.6}
	\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
	\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
	\definecolor{mydarkyellow}{rgb}{0.8941,0.5137,0.0706}
	% =================================================
    \textcolor{mydarkyellow}{v = 0}
    \tag{5}
\end{align}

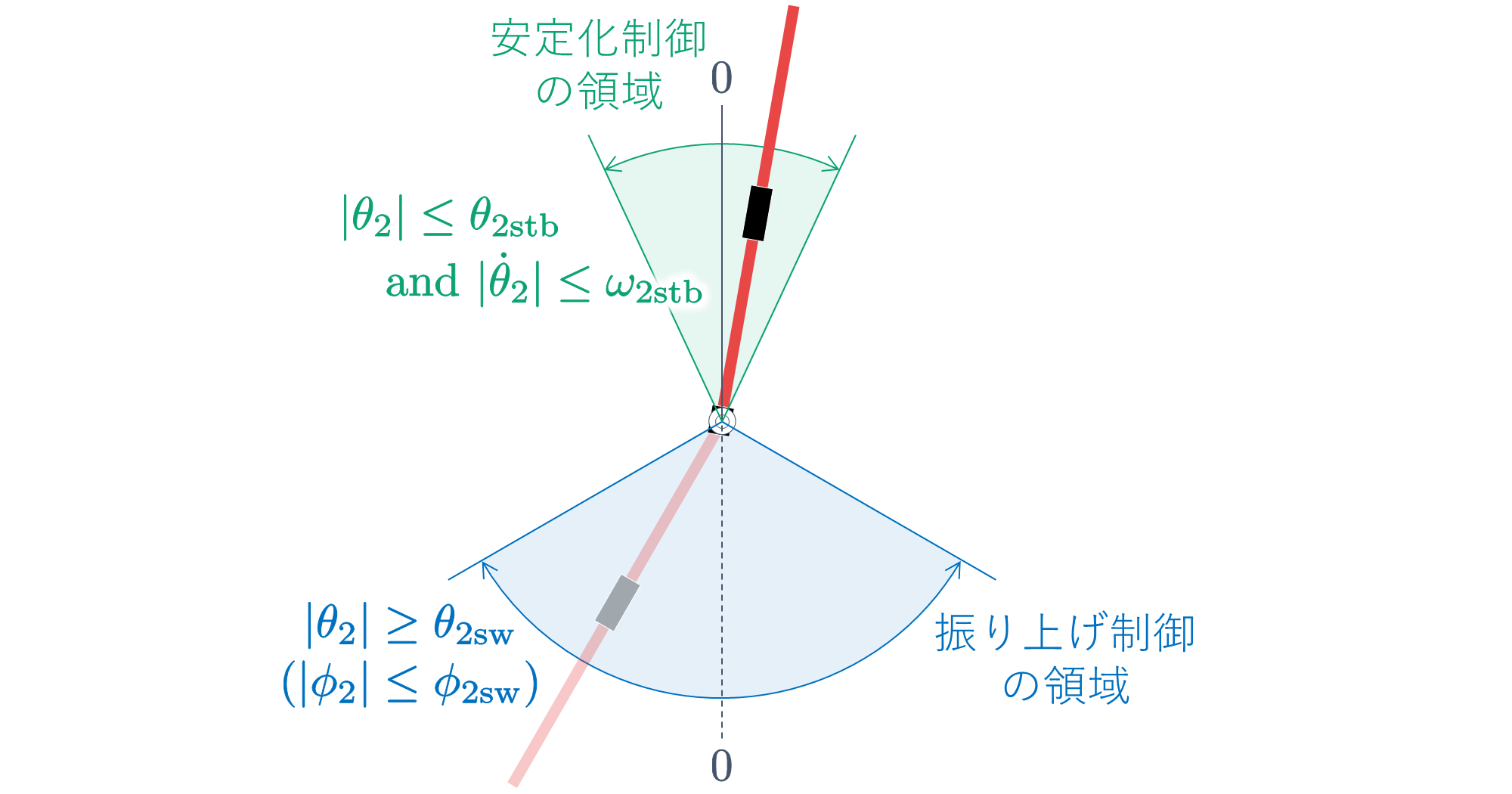
を切り替えます．切り替え条件としては，以下の点を考慮しました．

  • 振り上げ制御を行うのは，振子が真下から水平の少し手前までの領域とします．
  • 安定化制御を行うのは，振子の倒立付近の領域とします．ただし，この領域に入っていたとしても，振子の角速度が大きいときは，制御入力を $0$ として無制御とする（振子を惰性で回転させる）．
  • 振子の角度が上記の領域に入っていないときは，制御入力を $0$ として無制御とする（振子を惰性で回転させる）．

image.png

無制御の領域を比較的，大きく取りますが，これは，倒立付近での振子の角速度を抑えるためです．

　以上をまとめますと，振り上げ安定化の分岐処理は次式のようになります．

\begin{align}
	\require{color}
	\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
	\definecolor{myblue}{rgb}{0,0.4392,0.7529}
	\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
	\definecolor{mypink}{rgb}{1,0.4,0.6}
	\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
	\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
	\definecolor{mydarkyellow}{rgb}{0.8941,0.5137,0.0706}
	% =================================================
    v = \left\{\begin{array}{ll}
           \textcolor{myblue}{
            {f}_{\rm sw}(\dot{\theta}_{1},\,{\phi}_{2},\,\dot{\phi}_{2})} &
            \textcolor{myblue}{(|{\theta}_{2}| \ge {\theta}_{\rm 2sw})}
           \\
           \textcolor{mygreen}{
             {k}_{1}{\theta}_{1}
           + {k}_{2}\dot{\theta}_{1}
           + {k}_{3}{\theta}_{2}
           + {k}_{4}\dot{\theta}_{2}} &
          \textcolor{mygreen}{ (|{\theta}_{2}| \le {\theta}_{\rm 2stb}}\ \\
            & \quad 
          \textcolor{mygreen}{
            {\rm and}\ |\dot{\theta}_{2}| \le {\omega}_{\rm 2stb})}
           \\
          \textcolor{mydarkyellow}{0} & 
            \textcolor{mydarkyellow}{({\rm otherwise})}
    \end{array}\right.
    \tag{6}
\end{align}

2.3　Simulink ブロックでの実装

2.3.1　ステップ 1：ブロックの配置

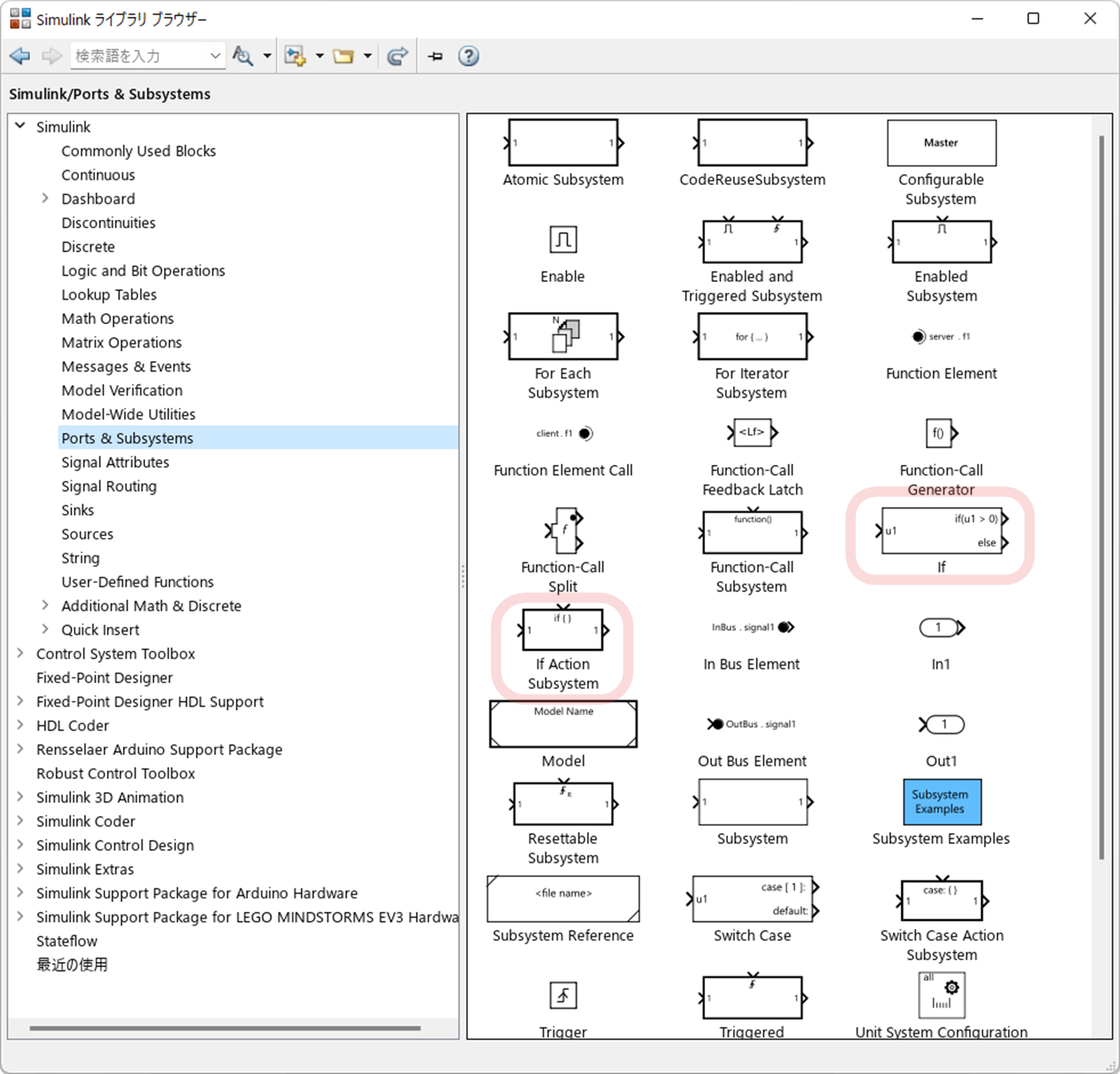
　$(6)$ 式の分岐処理を Simulink で実装するために，Simulink ブロック "If" や "If Action Subsystem" を使用します．これらの Simulink ブロックは，Simulink ライブラリ "Ports & Subsystems" に含まれています．

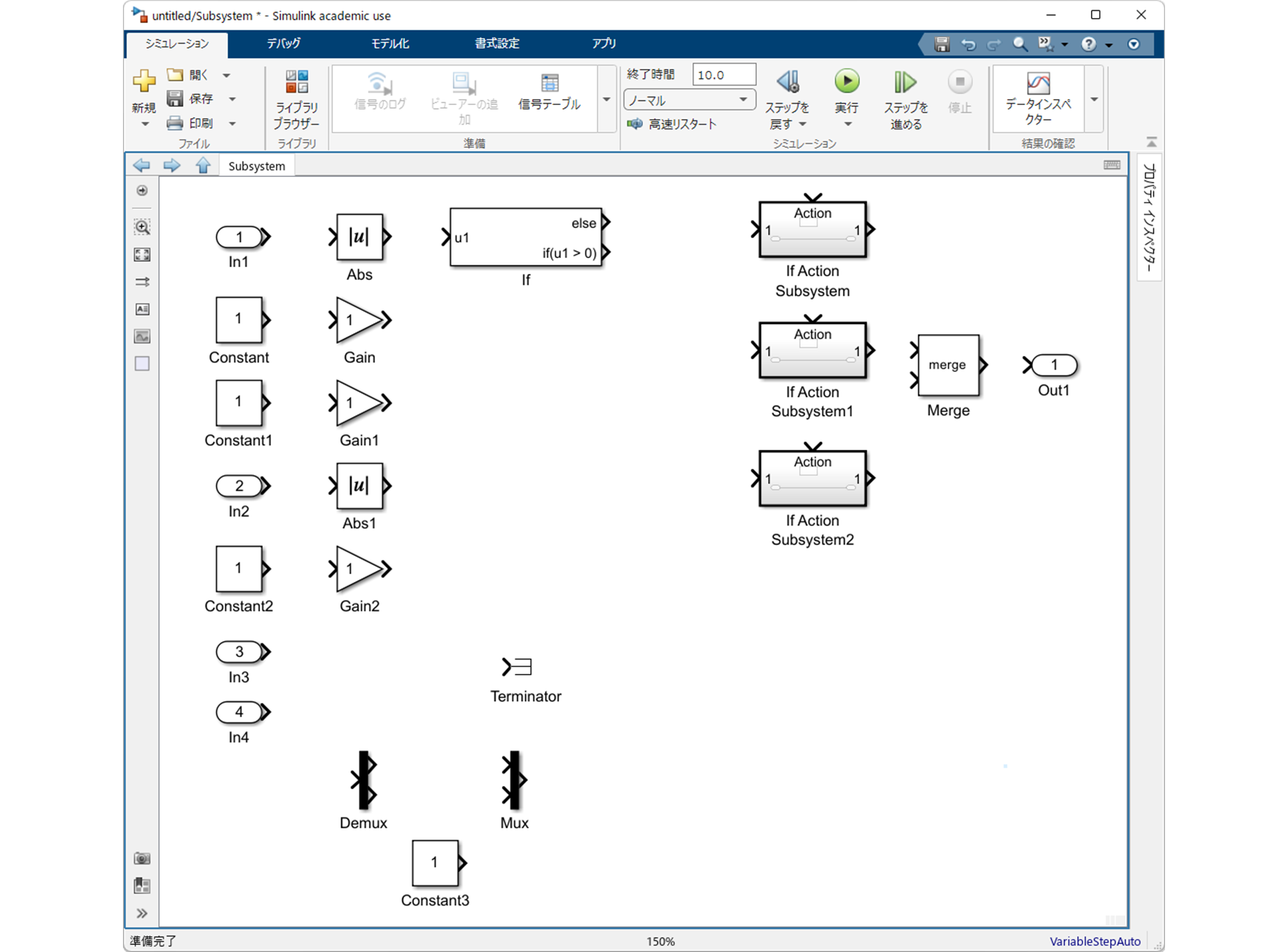
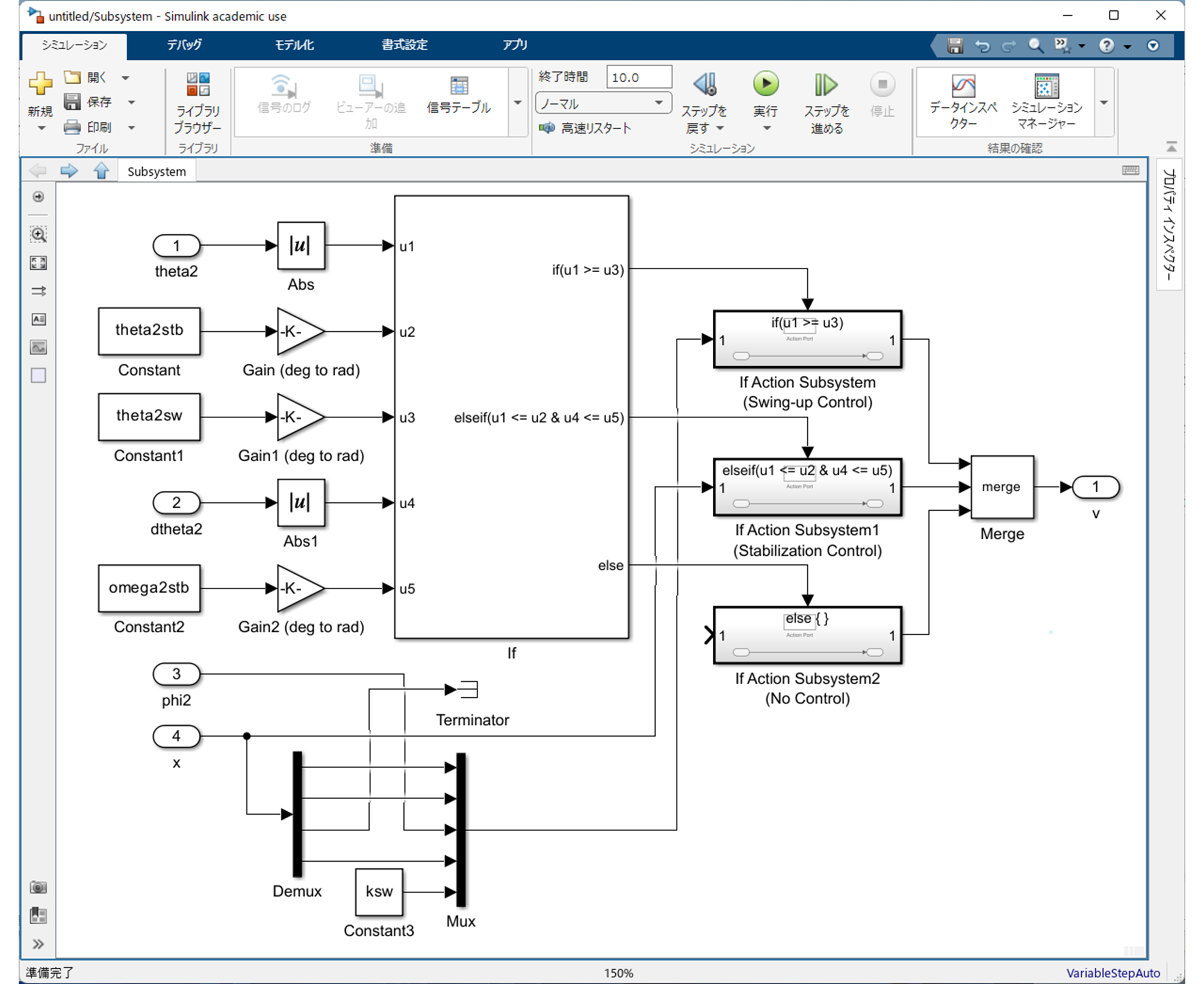
image.png

　まず，空の Simulink モデルに "Subsystem" を配置します．そして，"Subsystem" のなかに以下のように Simulink ブロックを配置します．

image.png

2.3.2　ステップ 2："If" の設定

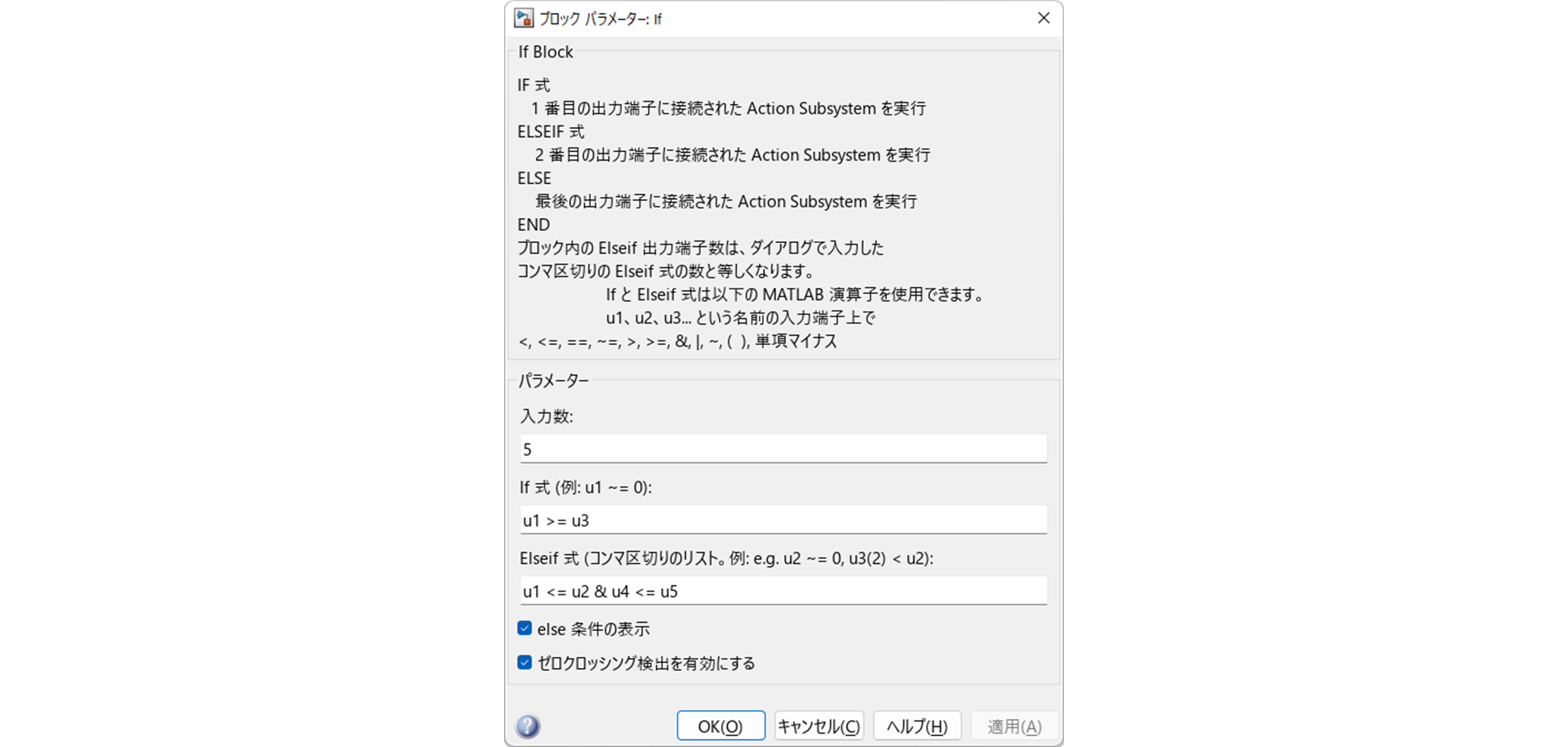
　"If" をダブルクリックし，

image.png

のように設定します．なお，

  • "If"
  • "If Action Subsystem" の Action

では，後述の設定により

  • u1：$|\theta_2|\ [{\rm rad}]$
  • u2：$\theta_{\rm 2stb}\ [{\rm rad}]$
  • u3：$\theta_{\rm 2sw}\ [{\rm rad}]$
  • u4：$|\dot{\theta}_{2}|\ [{\rm rad/s}]$
  • u5：$\omega_{\rm 2stb}\ [{\rm rad/s}]$

を意味していることに注意してください．つまり，"If" では，条件式を

if  u1 >= u3
  then 振り上げ制御
elseif u1 <= u2 and u4 <= u5
  then 安定化制御
else 無制御

と設定していることになります．

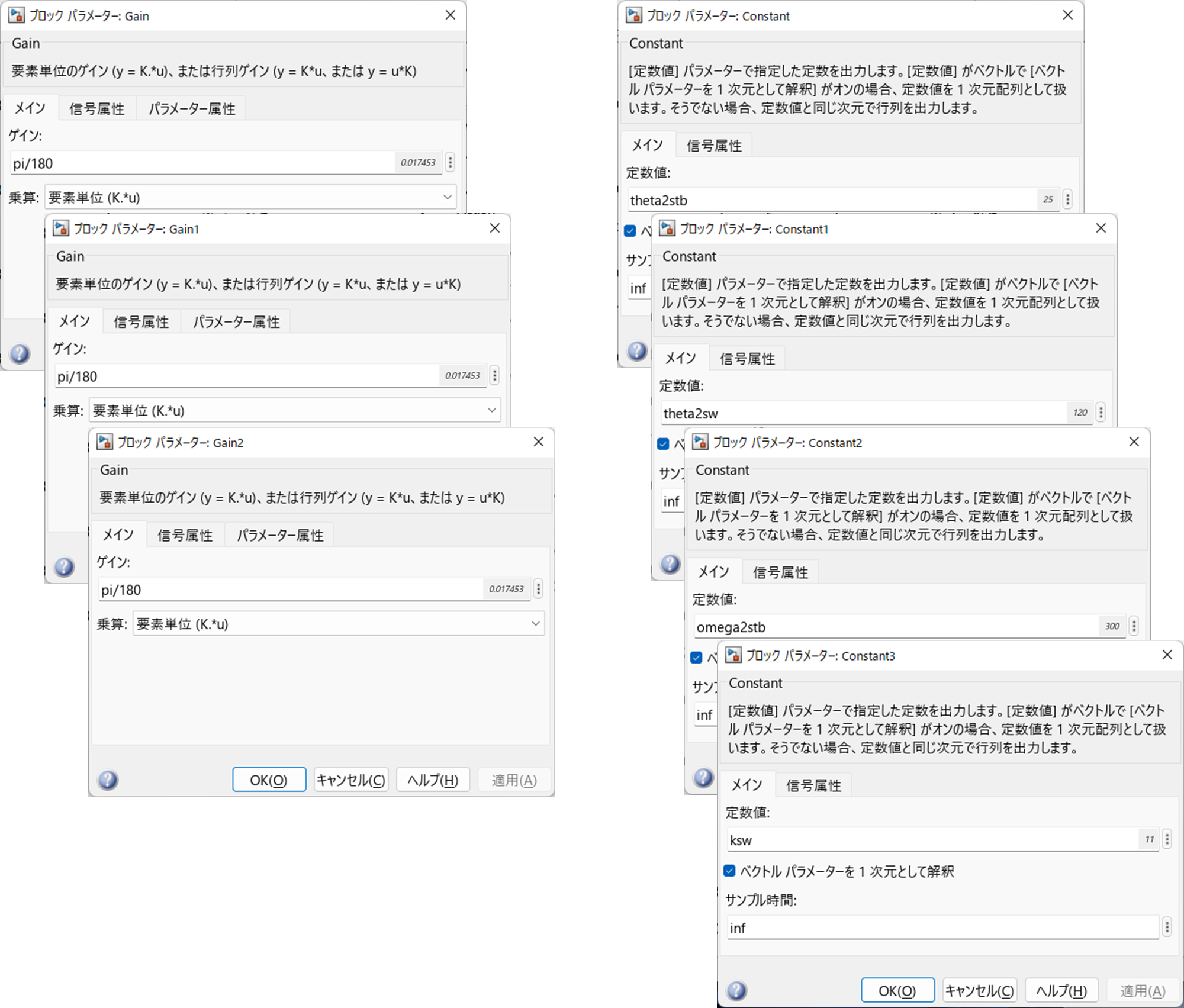
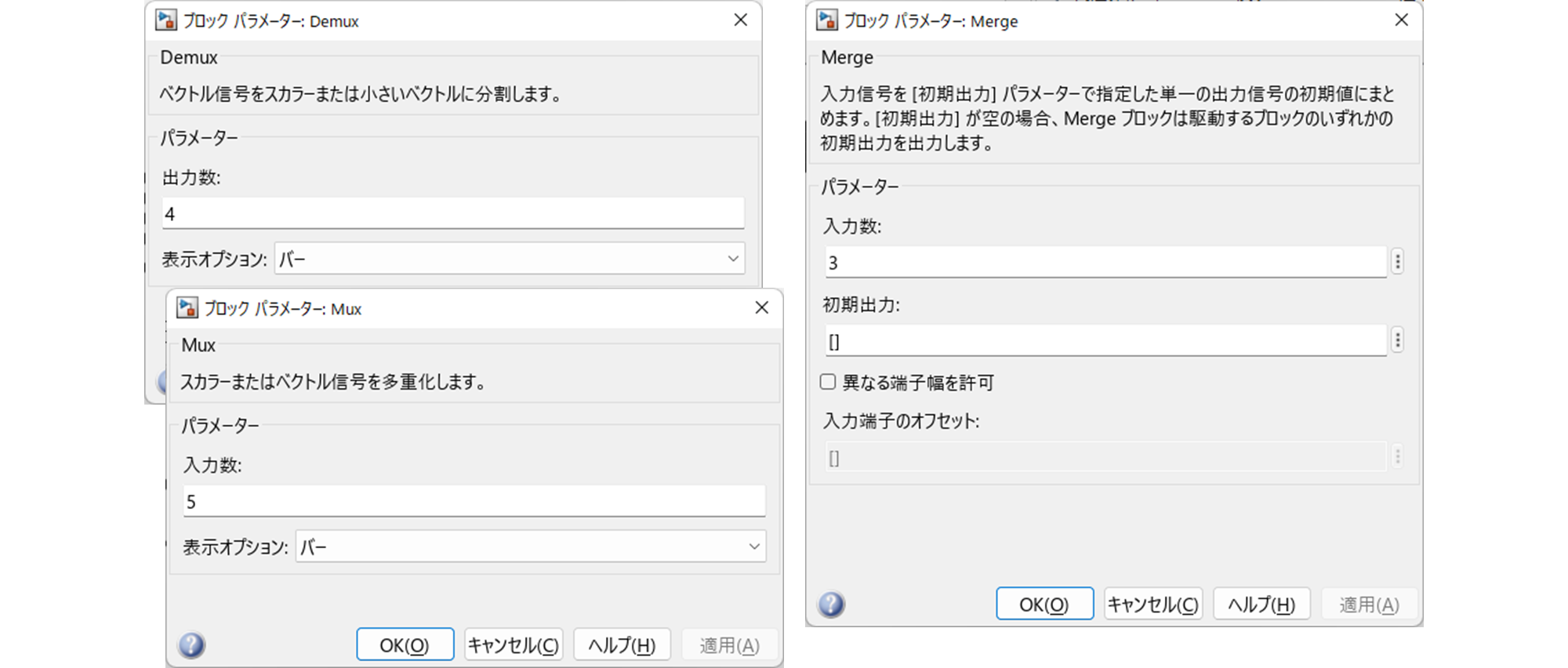
2.3.3　ステップ 3："Gain", "Constant", "Demux", "Mux", "Merge" の設定

　Simulink ブロック "Gain", "Constant", "Demux", "Mux", "Merge" は以下のように設定します．

image.png
image.png

2.3.4　ステップ 4：ブロックの結線

　Simulink ブロックの大きさや名前を適当に変更し，以下のように結線します．

image.png

2.3.5　ステップ 5："If Action Subsystem" の設定

　最後に，3 つの "If Action Subsystem" の設定を行います．"If Action Subsystem", "If Action Subsystem1", "If Action Subsystem2" の Action に "If" の分岐条件 (if, elseif, else) を結線していますので，それぞれに

  • "If Action Subsystem"：振り上げ制御
  • "If Action Subsystem1"：安定化制御
  • "If Action Subsystem2"：無制御

の操作を表現します．

(a) "If Action Subsystem" の設定

　"If Action Subsystem" では振り上げ制御のコントローラ $(3)$ 式を実装します．"If Action Subsystem" の入力端子 "In1" には "Mux" が結線されているので，"If Action Subsystem" のなかでは，

  • u(1)：$x_1 = \theta_1\ {\rm [rad]}$（アームの角度）
  • u(2)：$x_2 = \dot{\theta}_1\ {\rm [rad/s]}$（アームの角速度）
  • u(3)：$\phi_2\ {\rm [rad]}$（真下を基準とした振子の角度）
  • u(4)：$x_4 = \dot{\theta}_2 = \dot{\phi}_2\ {\rm [rad/s]}$（振子の角速度）
  • u(5)：$k_{\rm sw}$：振り上げゲイン

が使用できます．

　"If Action Subsystem" には以下のようにブロックを配置し，"Fcn" を設定したうえで結線します．

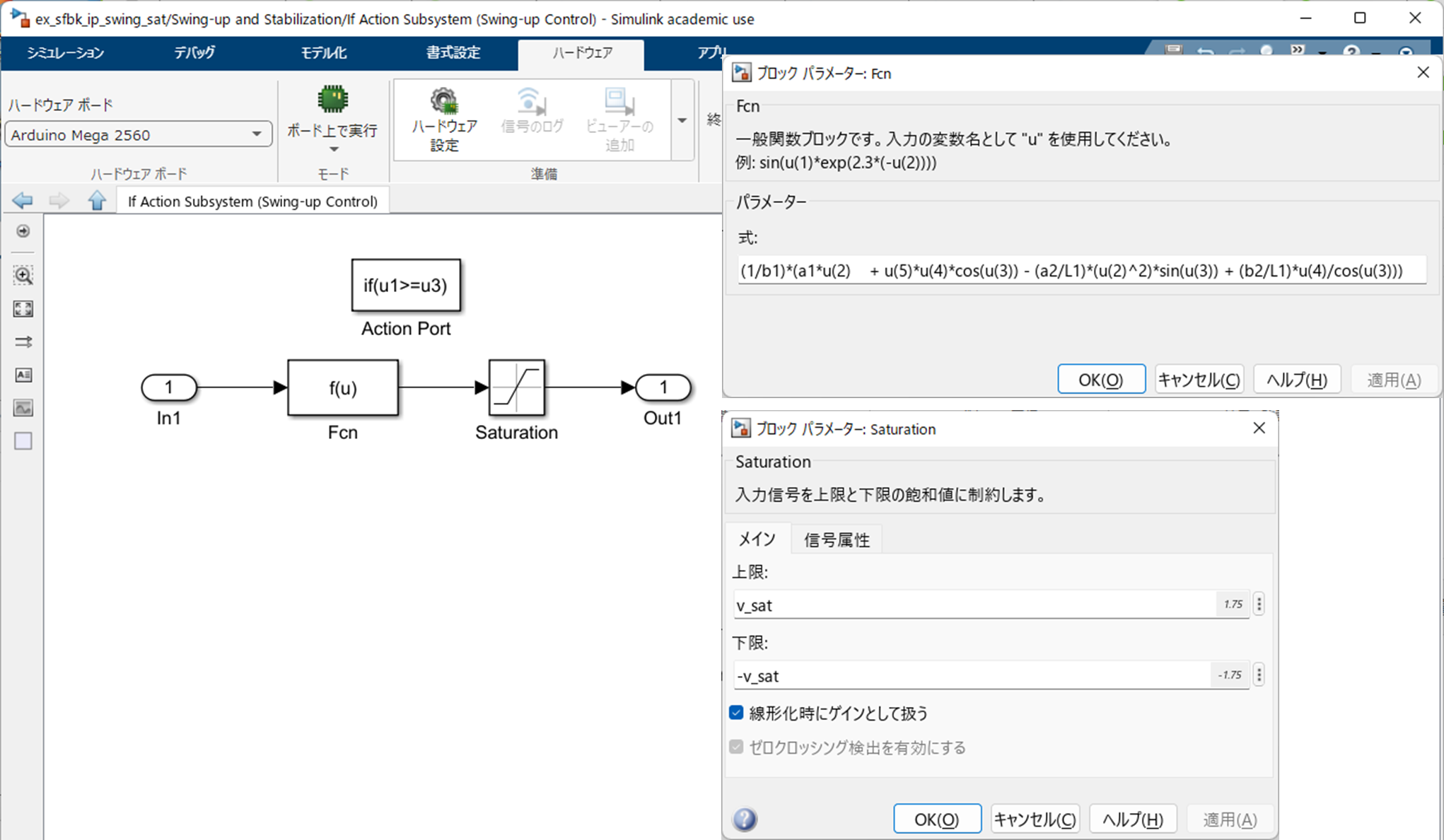image.png
"If Action Subsystem" におけるブロックの配置，設定および結線

"Fcn"（R2020b 以降の場合，付録 B を参照してください）では振り上げコントローラ $(3)$ 式の右辺

\begin{align}
	\require{color}
	\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
	\definecolor{myblue}{rgb}{0,0.4392,0.7529}
	\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
	\definecolor{mypink}{rgb}{1,0.4,0.6}
	\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
	\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
	\definecolor{mydarkyellow}{rgb}{0.8941,0.5137,0.0706}
	% =================================================
    \textcolor{myblue}{\dfrac{1}{{\beta}_{1}}\biggl(
            {\alpha}_{1}\dot{\theta}_{1}
            + {k}_{\rm sw}\dot{\phi}_{2}\cos{\phi}_{2}
            - \dfrac{{\alpha}_{2}}{{L}_{1}}
                \dot{\theta}{}_{1}^{2}\sin{\phi}_{2}
            + \dfrac{{\beta}_{2}}
                    {{L}_{1}}
              \dfrac{\dot{\phi}_{2}}
                    {\cos{\phi}_{2}}
        \biggr)}
\end{align}

を以下のように記述しています．

(1/b1)*(a1*u(2) + u(5)*u(4)*cos(u(3)) - (a2/L1)*(u(2)^2)*sin(u(3)) + (b2/L1)*u(4)/cos(u(3)))

また，振り上げコントローラ $(3)$ 式で生成された制御入力 $v$ をそのまま使用すると，倒立点付近での振子の回転速度が過大になり，安定化制御の切り替えがうまくいかないことがあります．そこで，"Saturation" を利用して制御入力の大きさを $|v| \le {v}_{\rm sat}$ のように制限し，振り上げコントローラ $(3)$ 式を

\begin{align}
    \textcolor{myblue}{
    v = \left\{\begin{array}{ll}
            -{v}_{\rm sat} & 
            (|\theta_2| \ge \theta_{\rm 2sw}\ {\rm and}\ v < -{v}_{\rm sat}) \\
            {f}_{\rm sw}(\dot{\theta}_{1},\,{\phi}_{2},\,\dot{\phi}_{2}) & 
            (|\theta_2| \ge \theta_{\rm 2sw}\ {\rm and}\ |v| \le {v}_{\rm sat}) \\
           {v}_{\rm sat} & 
            (|\theta_2| \ge \theta_{\rm 2sw}\ {\rm and}\ v > {v}_{\rm sat})
        \end{array}\right.
    }
    \tag{7}
\end{align}

のように修正します．

(b) "If Action Subsystem1" の設定

　"If Action Subsystem1" では安定化コントローラ $(4)$ 式を実装します．"If Action Subsystem1" の入力端子 "In1" には状態変数

\begin{align}
	\require{color}
	\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
	\definecolor{myblue}{rgb}{0,0.4392,0.7529}
	\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
	\definecolor{mypink}{rgb}{1,0.4,0.6}
	\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
	\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
	\definecolor{mydarkyellow}{rgb}{0.8941,0.5137,0.0706}
	% =================================================
    x = \left[\begin{array}{c}
            {x}_{1} \\
            {x}_{2} \\
            {x}_{3} \\
            {x}_{4} \\
        \end{array}\right]
    = \left[\begin{array}{c}
            {\theta}_{1} \\
            \dot{\theta}_{1} \\
            {\theta}_{2} \\
            \dot{\theta}_{2} \\
        \end{array}\right]
\end{align}

が入力されているので，以下のようにブロックを配置し，"Gain" を設定したうえで結線します．

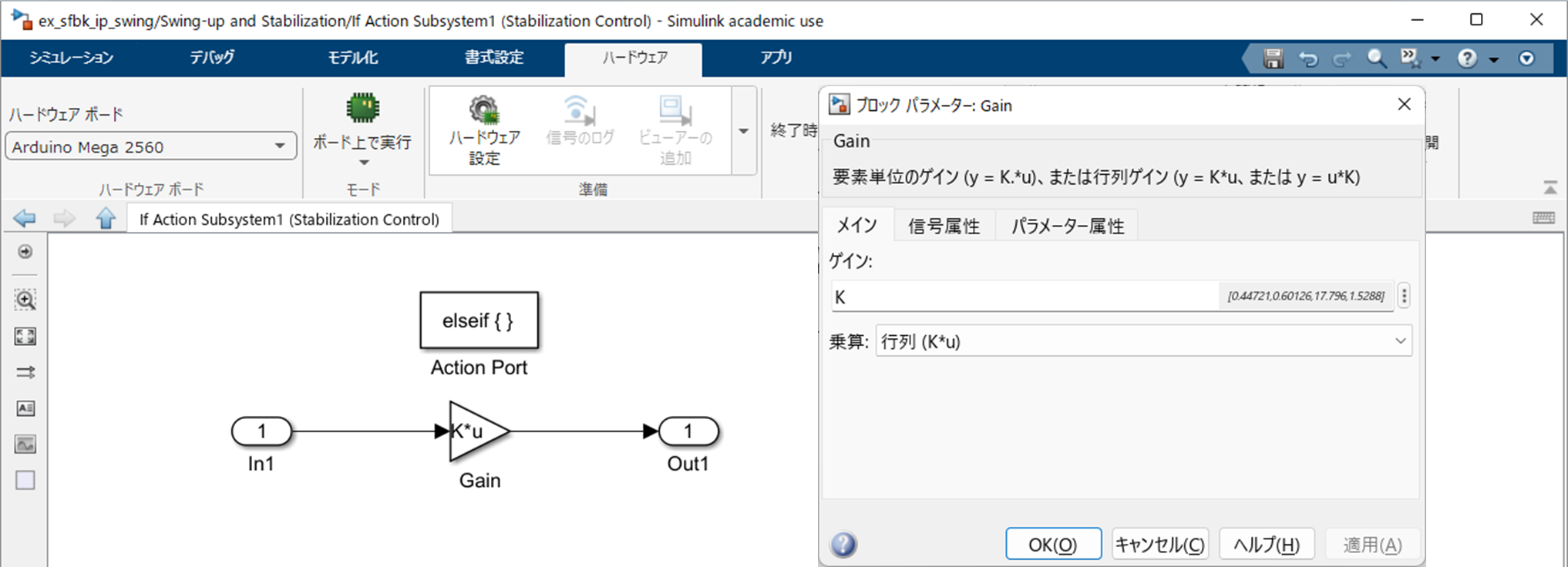image.png
"If Action Subsystem1" におけるブロックの配置，設定および結線

(c) "If Action Subsystem2" の設定

　"If Action Subsystem2" は無制御とした $(5)$ 式を実装します．入力端子は不要なので，"In1" を削除したうえで，以下のようにブロックを配置し，"Constant" を設定したうえで結線します．

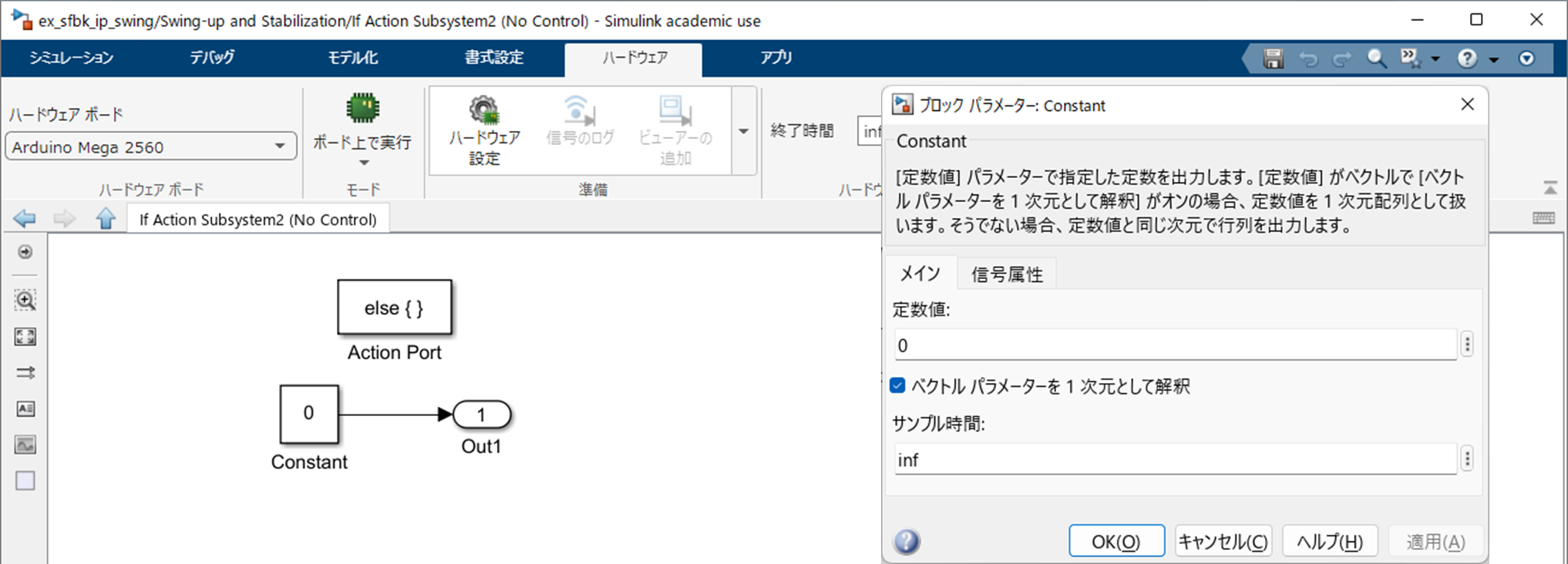image.png
"If Action Subsystem2" におけるブロックの配置，設定および結線

　以上の設定を行うと，振り上げ安定化を実現するコントローラ $(6)$ 式は，Simulink により以下のように実装されます．

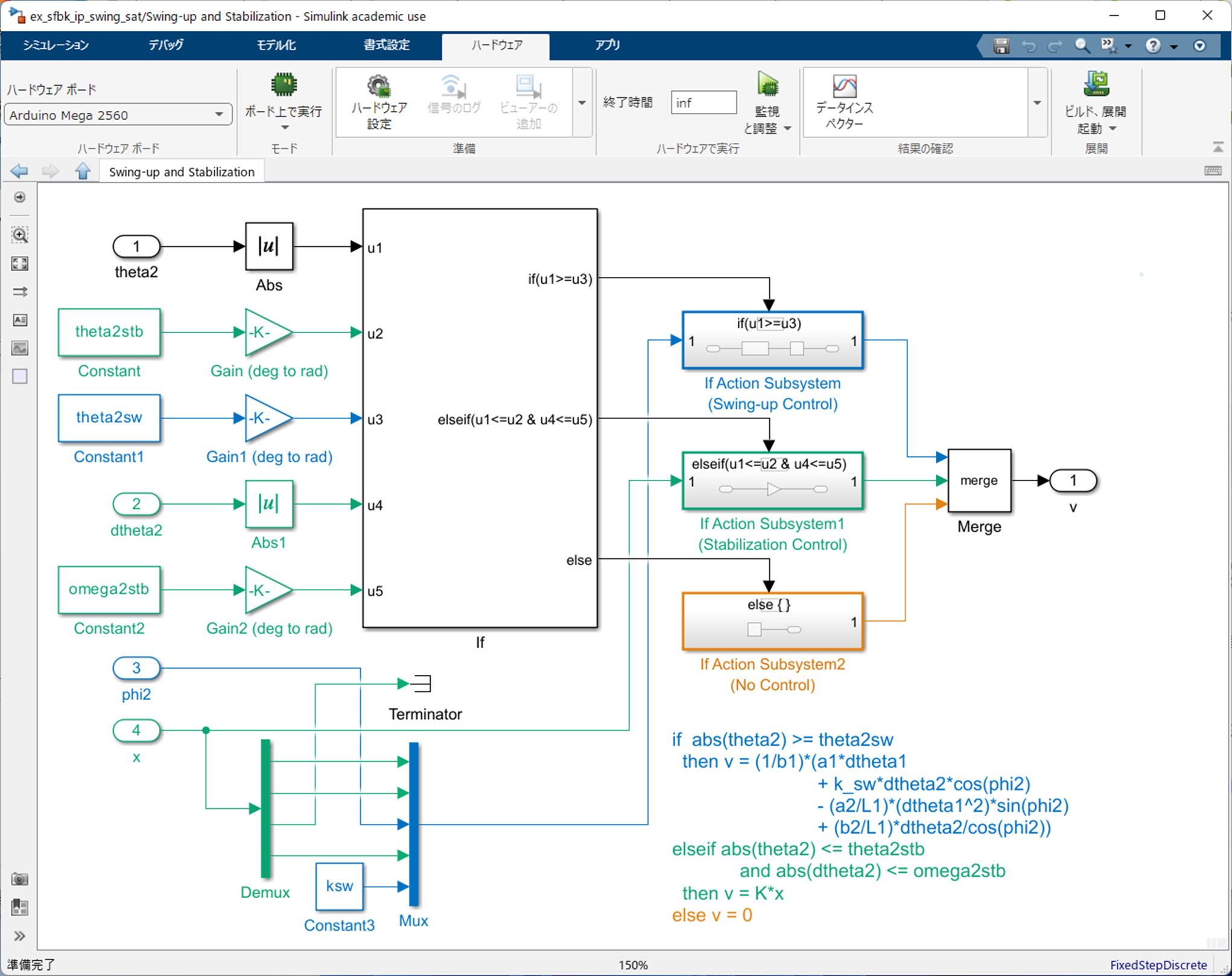image.png
振り上げ安定化コントローラ $(6)$ 式を Simulink により実装！！（Subsytem "Swing-up and Stabilization"）

3. 振り上げ安定化制御の実機実験

　実機実験は LEGO 倒立振子で行っています．実験装置の組み立てや，Simulink モデルにより実機を動かす方法などについては，

をご参照ください．マイコン部は MinSegShield のキットに含まれている Arduino 互換ボードと Shield を利用しています．

3.1　作成した Simulink モデル

　最終的に作成した Simulink モデル "ex_sfbk_ip_swing_sat.slx" を以下に示します．

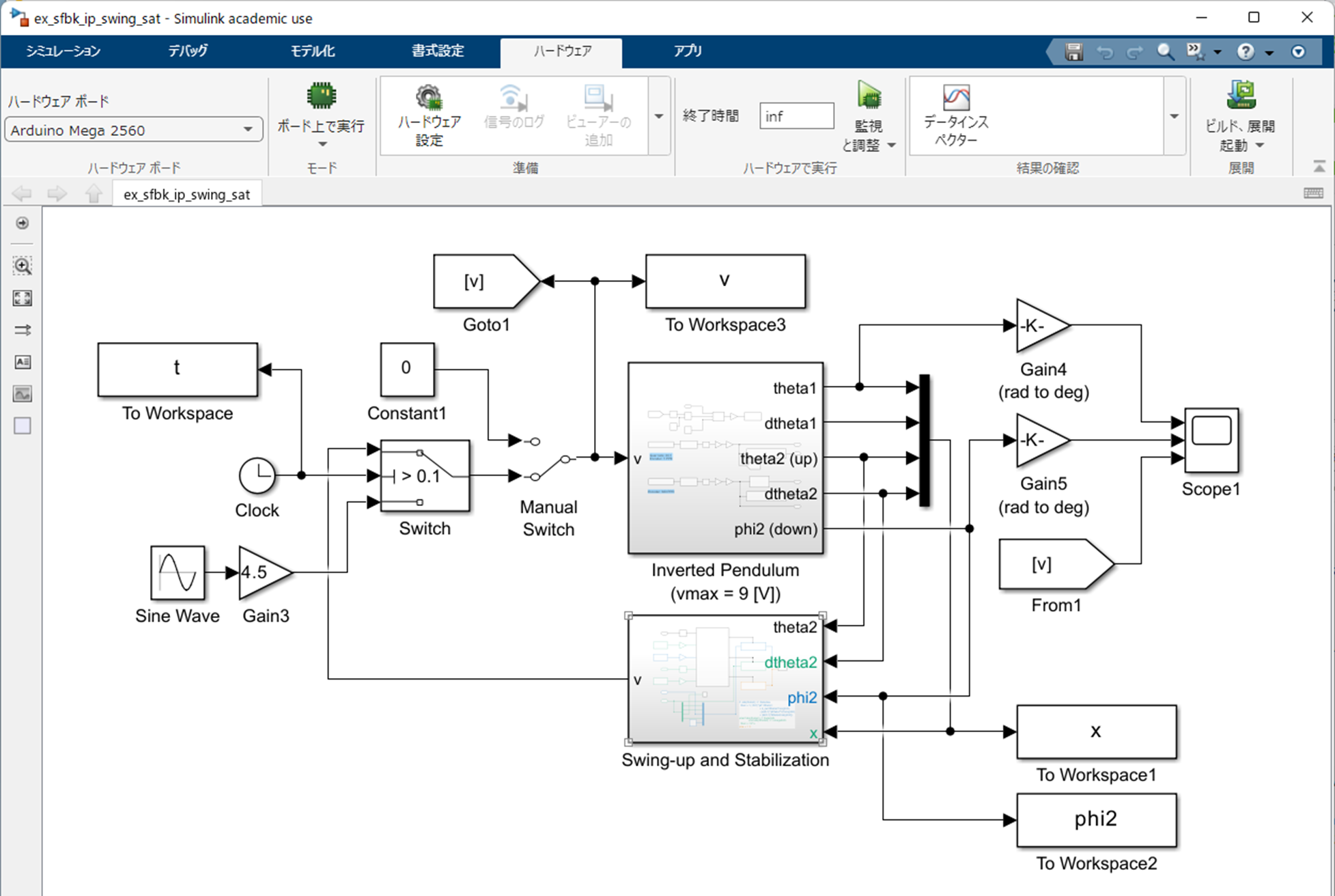image.png
Simulink モデル "ex_sfbk_ip_swing_sat.slx"

サンプリング周期は $h = 0.01\ {\rm [s]} = 10\ {\rm [ms]}$ とし，動的な部分は離散時間系で表現されています．

　なお，最初に振り上げ制御のトリガが必要ですので，最初の 0.1 秒間は "Sine Wave" と "Gain" により生成される正弦波（角周波数 15 [rad/s]，振幅 1 [V]）を 4.5 倍したものを制御入力 $v$ [V] として加えています．

　Simulink モデル "ex_sfbk_ip_swing_sat.slx" の詳しい設定は，実際に Simulink モデル "ex_sfbk_ip_swing_sat.slx" をダウンロードして確認していただければと思いますが，以下に，いくつか補足します．

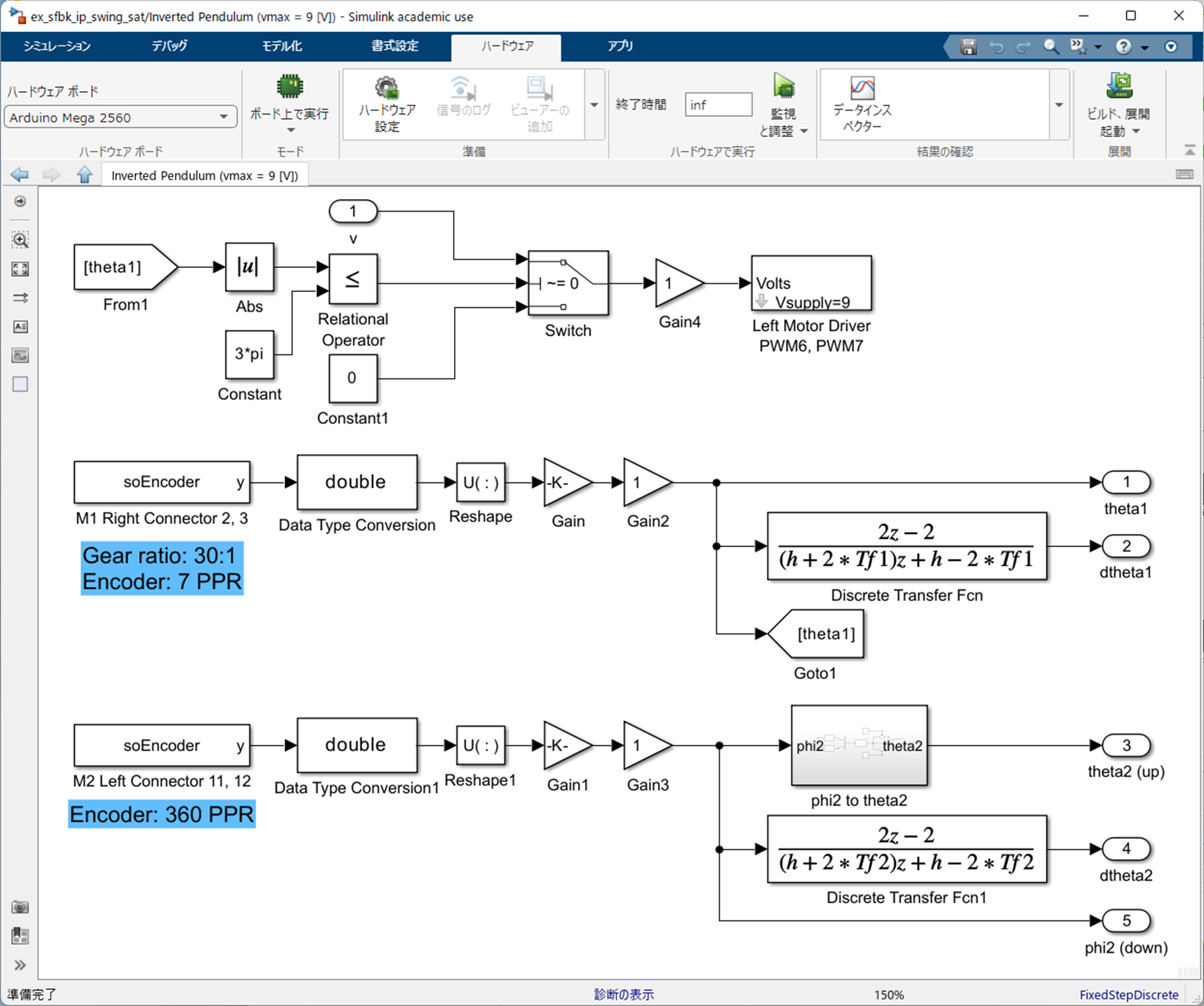image.png
Subsytem "Inverted Pendulum"

Subsytem "Inverted Pendulum"

  • Subsytem "Inverted Pendulum" は上記のように記述されています．MinSeg 社の Simulink ライブラリ Rensselaer Arduino Support Package Library (RASPLib) で提供されている "M1 Right Connector 2, 3" によりアーム角度 $\theta_1$ を，"M2 Left Connector 11, 12" により振子角度を取り込んでいます．また，"Left Motor Driver PWM6, PWM7" によりモータを駆動しています（制限電圧 $|v| \le 9\ {\rm [V]}$）．

  • "Gain", "Gain1" はそれぞれカウント数（4 逓倍）から角度への変換係数です．また，"Gain2", "Gain3", "Gain4" は，正転・逆転の方向を決める係数です（想定の回転方向と逆の場合は -1 に設定します）．

  • 暴走を防ぐため，Subsytem "Inverted Pendulum" において，アーム角度が 1 回転半を超える ($|\theta_1| > 3\pi\ {\rm [rad]}$) と，無制御 ($v = 0$) となるようにしています．

不完全微分器の離散化
角度から角速度への変換には，不完全微分器（微分器と 1 次のローパスフィルタの直列結合）

\begin{align}
    G_{{\rm f}i}(s) = \dfrac{s}{1 + T_{{\rm f}i}s}\ 
    (i = 1,\,2)
    \tag{8}
\end{align}

を双 1 次変換（台形近似）により離散化した

\begin{align}
    G_{{\rm f}i}(s)|_{s = \frac{2}{h}\frac{z - 1}{z + 1}} 
    = \dfrac{2z - 2}{(h + 2T_{{\rm f}i})z + h - 2T_{{\rm f}i}}\ (i = 1,\,2)
    \tag{9}
\end{align}

が使用されています．ただし，$z$ はシフトオペレータであり，1 サンプリングの進みを意味します．

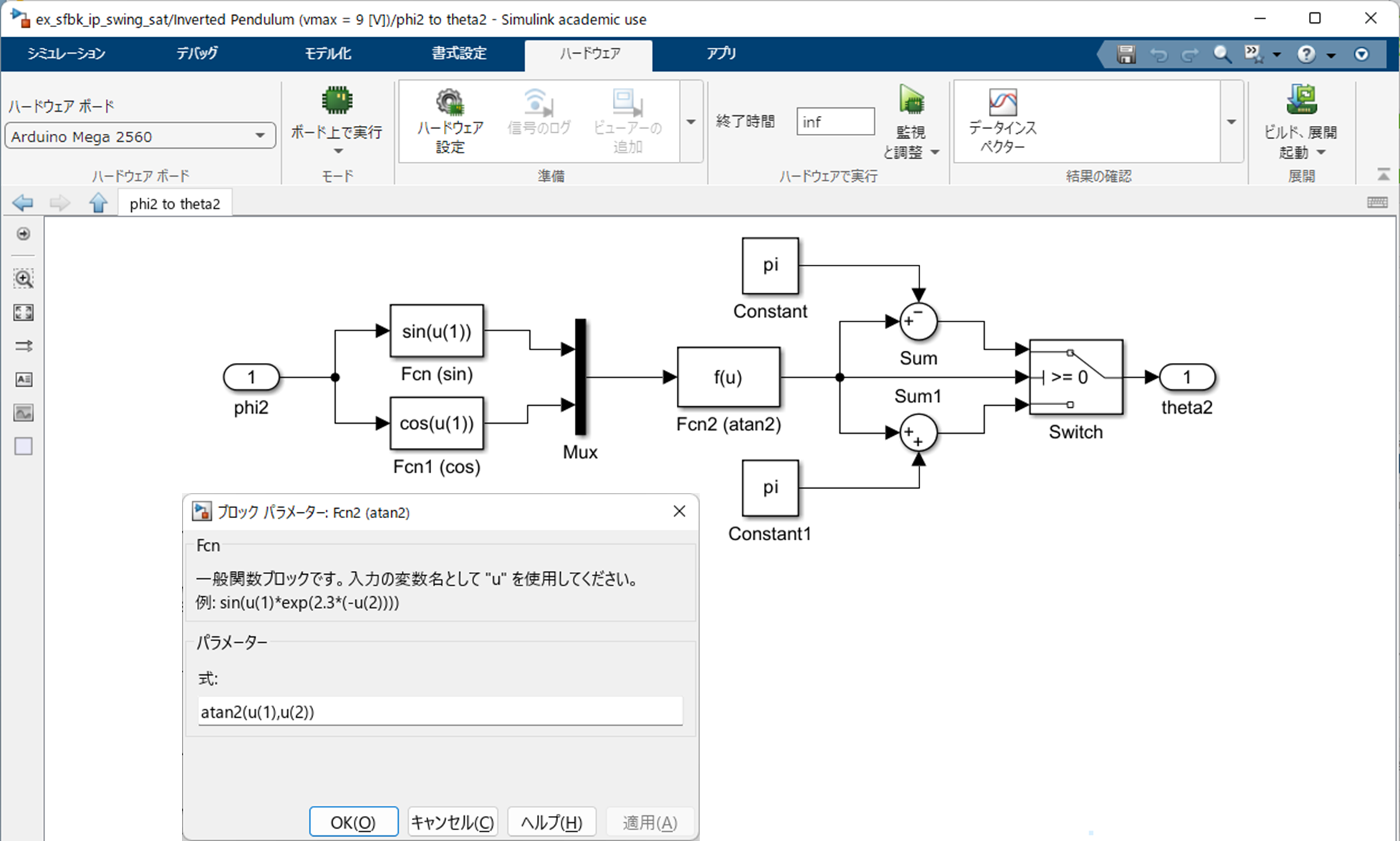image.png
Subsytem "phi2 to theta2"

Subsytem "phi2 to theta2"
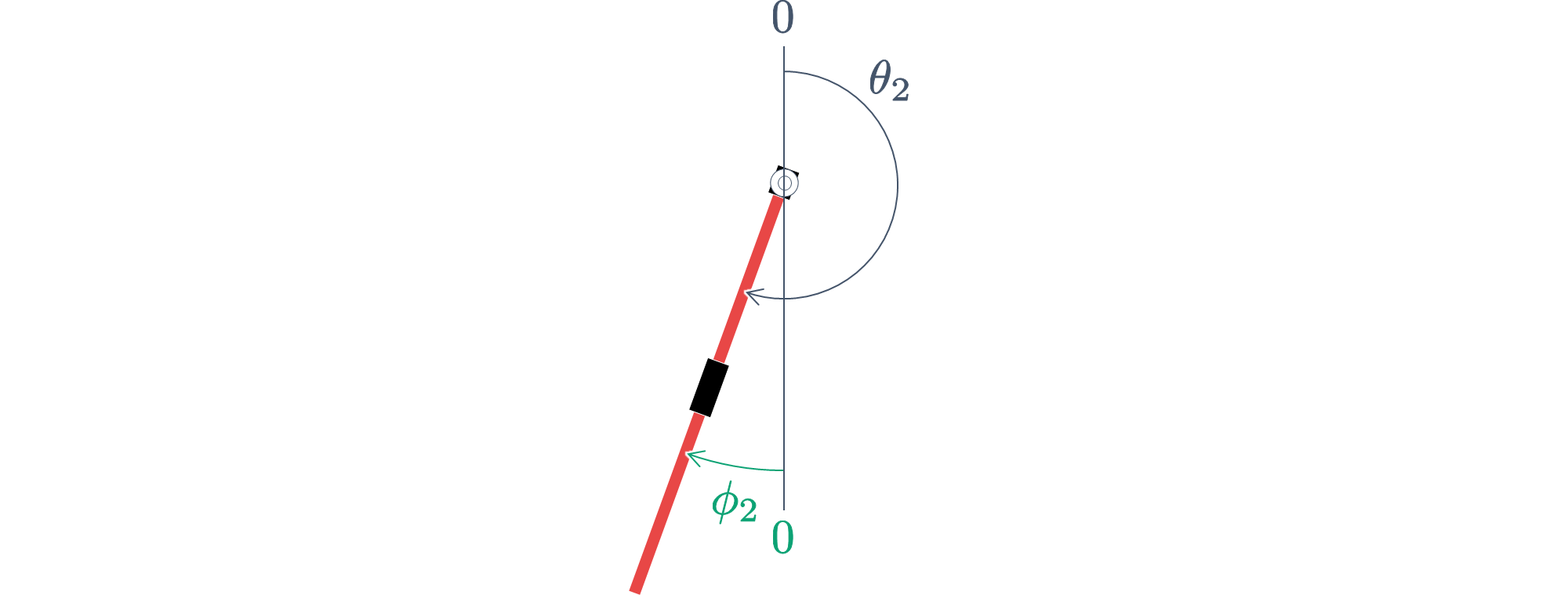
Subsytem "Inverted Pendulum" に含まれる Subsytem "phi2 to theta2" は，振子角度を真下基準の $\phi_2$ から真上基準の $\theta_2$ に変換するために作成しました．

  • この Subsytem では，"Fcn (sin)" により $\sin\phi_2$ を，"Fcn1 (cos)" により $\cos\phi_2$ を生成し，これらを "Fcn2 (atan2)" により逆正接の操作 $
    \tan^{-1}\dfrac{\sin\phi_2}{\cos\phi_2}
    $ を行っています．"atan2" を使用していますので，この操作により振子が 1 回転以上の回転をしたときでも，常に $|\phi_2| \le \pi$ の振子角度 $\phi_2$ が得られます．

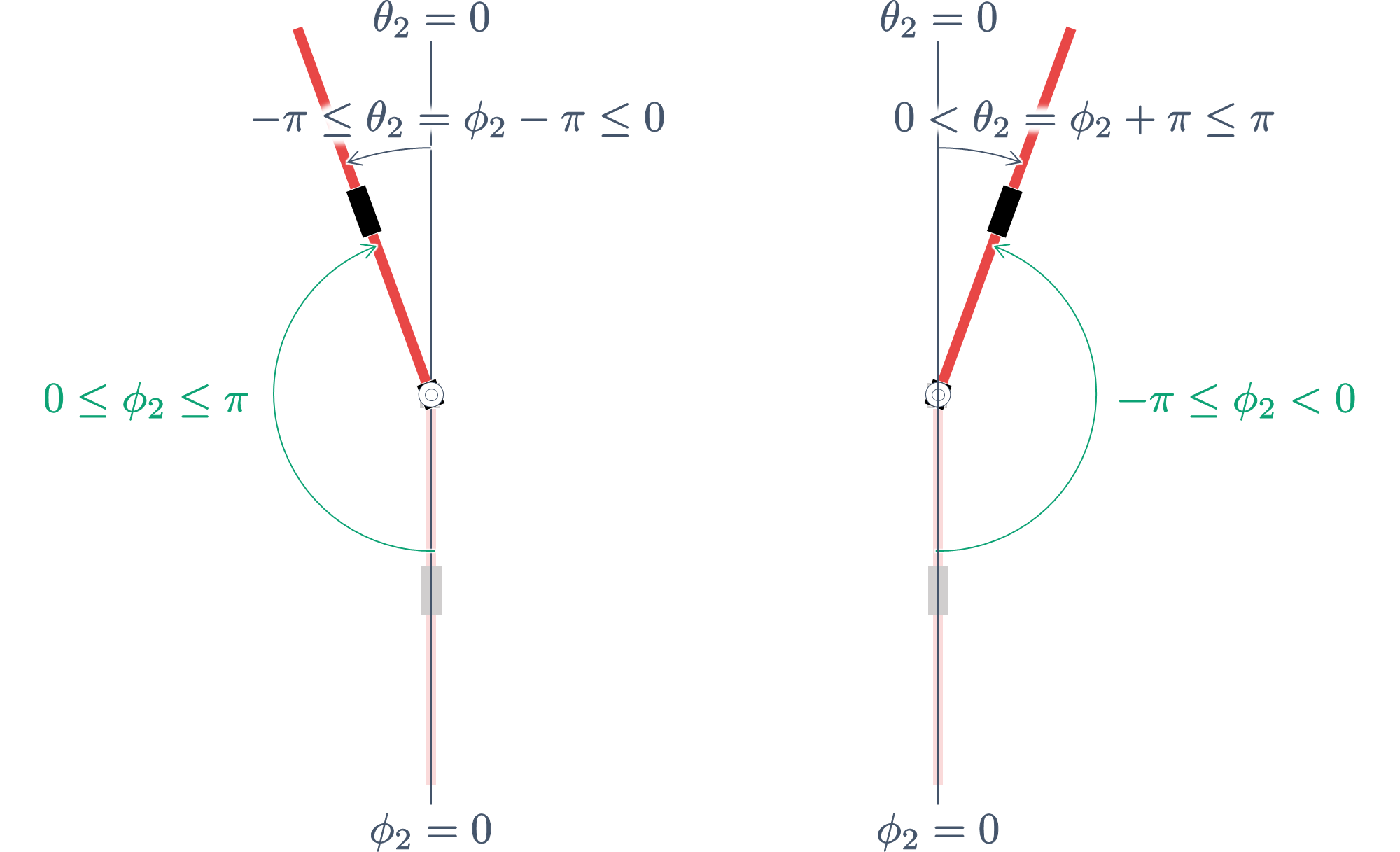
  • $|\phi_2| \le \pi$ の真下基準の振子角度 $\phi_2$ を，次式により真上基準の振子角度 $\theta_2$ に変換します（このとき，$|\theta_2| \le \pi$ となります）．

\begin{align}
    \theta_2 = \left\{\begin{array}{ll}
			\phi_2 - \pi & (0 \le \phi_2 \le \pi) \\
			\phi_2 + \pi & (-\pi \le \phi_2 < 0) 
        \end{array}\right.
    \tag{10}
\end{align}

image.png

3.2　M ファイル

　実験を行う前に，

  • サンプリング周期 $h$ の設定
  • 不完全微分の時定数 $T_{{\rm f}1}$, $T_{{\rm f}2}$ の設定
  • 分岐処理を行うための角度や角速度のしきい値の設定
  • 振り上げゲイン $k_{\rm sw}$ の設定
  • 最適レギュレータによる安定化コントローラのゲイン $K$ の設計

を行う必要があります．そのための M ファイルを以下に示します．

M ファイル "ip_design_sat.m"
clear
format compact

h = 0.01;        % サンプリング周期

Tf1 = 0.08;      % ローパスフィルタの時定数
Tf2 = 0.08;      % ローパスフィルタの時定数

% =============================================
% If Action Subsystem (Swing-up Control) で
% Saturation を使用する場合（上限：1.75 [V]）

theta2stb =  25; % deg
omega2stb = 300; % deg/s
theta2sw  = 120; % deg

ksw   = 8;       % 振り上げゲイン
v_sat = 1.75;    % 振り上げ制御時の制御入力の上限値

% =============================================
g  = 9.81e+00;
L1 = 7.00e-02;

a1 = 1.53e+01;
b1 = 7.06e+01;

a2 = 1.10e-01;
b2 = 3.59e-02;

E = [ 1  0  0  0
      0  1  0  0
      0  0  1  0
      0  L1 0  a2 ];
F = [ 0  1  0  0
      0 -a1 0  0
      0  0  0  1
      0  0  g -b2 ];
G = [ 0
      b1
      0
      0 ];

disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp(' システム行列 A, B')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')

A = inv(E)*F
B = inv(E)*G

disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp(' 重み行列 Q, R')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')

q1 = 0.2;
q3 = 100;

Q = diag([q1 0 q3 0])
R = 1

disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp(' 最適レギュレータによるコントローラゲイン K')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')

K = -lqr(A,B,Q,R)

disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp(' A + B*K の固有値')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')

eig(A + B*K)

M ファイル "ip_design_sat.m" を実行すると，以下の結果が得られます．

M ファイル "ip_design_sat.m" の実行結果
>> ip_design
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
 システム行列 A, B
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
A =
         0    1.0000         0         0
         0  -15.3000         0         0
         0         0         0    1.0000
         0    9.7364   89.1818   -0.3264
B =
         0
   70.6000
         0
  -44.9273
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
 重み行列 Q, R
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
Q =
    0.2000         0         0         0
         0         0         0         0
         0         0  100.0000         0
         0         0         0         0
R =
     1
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
 最適レギュレータによるコントローラゲイン K
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
K =
    0.4472    0.6013   17.7962    1.5288
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
 A + B*K の固有値
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
ans =
 -18.7279 +12.1869i
 -18.7279 -12.1869i
  -2.2029 + 0.8872i
  -2.2029 - 0.8872i

3.3　実機実験

　振り上げ安定化制御の実機実験を「エクスターナルモード（監視と調整）」で行うと，以下のようになります．

  • さほど強くつついていないときは，倒れずに倒立を維持しています．
  • 少し強めにつつくと，振子は倒れますが，速やかに倒立状態に復帰します．
  • 強めにつつくと，振子は倒れた後，何回か回転しますが，徐々に回転速度が減少し，倒立状態に復帰します．

　一方で，振子の角度や角速度の制約が適切でないと，振子が荒ぶれます！　これが LEGO じゃなかったら危険です！

っていうか，荒ぶっている方が再生回数が多いとは・・・

4. おわりに

　本記事では，回転型倒立振子の振り上げ安定化制御を，Simulink の分岐処理により実現する方法を説明しました．実機実験を行うために，結構，ゴリゴリの作業をしていることがわかります．この手の解説記事はあまり見当たらないと思います（査読付論文に投稿するような内容ではない）ので，皆さまの参考になれば幸いです．

image.png

参考文献

  1. https://en.wikipedia.org/wiki/Furuta_pendulum

  2. 川田昌克（編著）・東　俊一・市原裕之・浦久保孝光・大塚敏之・甲斐健也・國松禎明・澤田賢治・永原正章・南　裕樹： 倒立振子で学ぶ制御工学， 森北出版 (2017.2.28)（とくに，第 II 部 (発展編) 第 3 章 非線形制御 3.2.1 エネルギー法：浦久保先生のご担当分）　$\cdots$$\cdots$ サポートページ

おまけ

　ここまで読んで，「実機実験じゃなくてシミュレーションだけしたい！」と思った方，安心してください．ファイルを公開していています．詳細の説明をする余力はありませんが…

付録 A　振り上げコントローラ

　振り上げ制御を行うために，振子の力学的エネルギーが増大するように制御入力を加えることにします．

　倒立振子の非線形モデルは $(1)$, $(2)$ 式に示したように，

\begin{align}
	\require{color}
	\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
	\definecolor{myblue}{rgb}{0,0.4392,0.7529}
	\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
	\definecolor{mypink}{rgb}{1,0.4,0.6}
	\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
	\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
	% =================================================
	\ddot{\theta}_{1}
    &=
	{}- {\alpha}_{1}\dot{\theta}_{1} 
	+ {\beta}_{1}v 
	\tag{A.1}
	% --------
	\\
	&\hspace{-2cm}
    {m}_{2}{L}_{1}{l}_{2}\cos{\theta}_{2}\cdot\ddot{\theta}_{1}
		+ {J}_{2}\ddot{\theta}_{2}
	\\
	&
	= {J}_{2}\dot{\theta}{}_{1}^{2}\sin{\theta}_{2}\cos{\theta}_{2}
		+ {m}_{2}g{l}_{2}\sin{\theta}_{2}
		- {c}_{2}\dot{\theta}_{2}
	\tag{A.2}
\end{align}

で与えられます．
image.png
　振子の力学的エネルギー $E$ は

\begin{align}
    E = \dfrac{1}{2}{J}_{2}\dot{\theta}{}_{2}^{2} 
      + {m}_{2}gh > 0
    \tag{A.3}
\end{align}

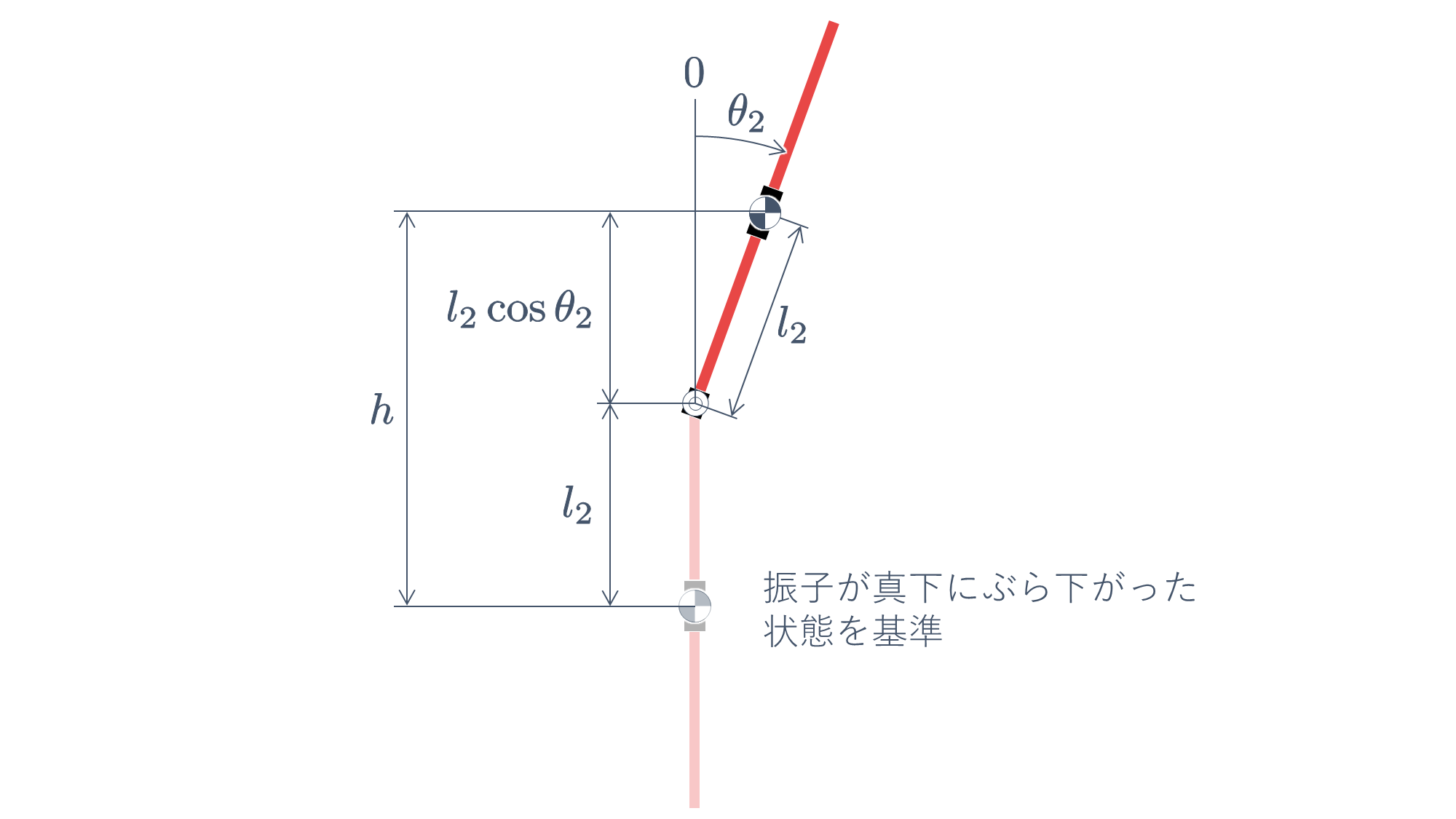
となります．ここで，振子がぶら下がった状態を基準とした重心位置の高さ $h$ は

\begin{align}
    h = {l}_{2} + {l}_{2}\cos{\theta}_{2}
      = {l}_{2}(1 + \cos{\theta}_{2})
\end{align}

ですので，$\rm (A.3)$ 式は

\begin{align}
    E = \dfrac{1}{2}{J}_{2}\dot{\theta}{}_{2}^{2} 
      + {m}_{2}g{l}_{2}(1 + \cos{\theta}_{2}) > 0
    \tag{A.4}
\end{align}

となり，常に正です．この振子の力学的エネルギー $E$ を増大させるために，

  • 力学的エネルギー $E$ を単調増加させる $(E > 0,\ \dot{E} > 0)$

ことにします．

　力学的エネルギー $E$ の時間微分を求めると，$\rm (A.4)$ 式より

\begin{align}
    \dot{E} = \dot{\theta}_{2}\bigl(
                {J}_{2}\ddot{\theta}_{2}
                - {m}_{2}g{l}_{2}\sin{\theta}_{2}
            \bigr)
    \tag{A.5}
\end{align}

となります．ここで，$\rm (A.2)$ 式および $\rm (A.1)$ 式より

\begin{align}
	&{J}_{2}\ddot{\theta}_{2} - {m}_{2}g{l}_{2}\sin{\theta}_{2}
	\\
	&\qquad
	= {J}_{2}\dot{\theta}{}_{1}^{2}\sin{\theta}_{2}\cos{\theta}_{2}
		- {c}_{2}\dot{\theta}_{2}
		- {m}_{2}{L}_{1}{l}_{2}\cos{\theta}_{2}\cdot\ddot{\theta}_{1} 
    \\
	&\qquad
	= {J}_{2}\dot{\theta}{}_{1}^{2}\sin{\theta}_{2}\cos{\theta}_{2}
		- {c}_{2}\dot{\theta}_{2}
	\\
    &\qquad\qquad\qquad{}
		- {m}_{2}{L}_{1}{l}_{2}\cos{\theta}_{2}\cdot
    		\bigl(
                {}- {\alpha}_{1}\dot{\theta}_{1} + {\beta}_{1}v
            \bigr) 
    \tag{A.6}
\end{align}

となります．したがって，$\rm (A.6)$ 式を $\rm (A.5)$ 式に代入すると，

\begin{align}
    \dot{E} = \dot{\theta}_{2}\bigl\{
                  & {J}_{2}\dot{\theta}{}_{1}^{2}\sin{\theta}_{2}\cos{\theta}_{2}
                		- {c}_{2}\dot{\theta}_{2}
                	\\
                  &\hspace{1.3cm} {}
                	- {m}_{2}{L}_{1}{l}_{2}\cos{\theta}_{2}\cdot
                   	\bigl(
                        {}- {\alpha}_{1}\dot{\theta}_{1} + {\beta}_{1}v
                    \bigr) 
            \bigr\}
    \tag{A.7}
\end{align}

が得られます．

　つぎに，$\rm (A.7)$ 式に基づいて，力学的エネルギー $\pmb{E}$ を単調増加させる $(E > 0,\ \dot{E} > 0)$ ような制御入力 $v$ を生成します．このような制御入力 $v$ のひとつとして，力学的エネルギーの時間微分 $\dot{E}$ が

\begin{align}
    \dot{E} = {k}_{\rm sw}{m}_{2}{L}_{1}{l}_{2}
                (\dot{\theta}_{2}\cos{\theta}_{2})^{2}
    > 0
    \quad (\dot{\theta}_{2} \neq 0\ {\rm and}\ \cos{\theta}_{2} \neq 0)
    \tag{A.8}
\end{align}

となるように選ぶことにします．ただし，${k}_{\rm sw} > 0$ は設計者が与える振り上げゲインです．

$\rm (A.8)$ 式となるような制御入力 $v$ は，$\rm (A.7)$ 式と $\rm (A.8)$ 式が等しいという関係から，

\begin{align}
    & \phantom{\;\Longrightarrow\quad}
    {J}_{2}\dot{\theta}{}_{1}^{2}\sin{\theta}_{2}\cos{\theta}_{2}
                		- {c}_{2}\dot{\theta}_{2}
    \\
    &\hspace{2cm}{}
    - {m}_{2}{L}_{1}{l}_{2}\cos{\theta}_{2}\cdot
        \bigl(
        {}- {\alpha}_{1}\dot{\theta}_{1} + {\beta}_{1}v
        \bigr)
    = {k}_{\rm sw}{m}_{2}{L}_{1}{l}_{2}\dot{\theta}_{2}\cos^{2}{\theta}_{2}
    \\
    & \Longrightarrow\quad
    \dfrac{{J}_{2}}{{m}_{2}{L}_{1}{l}_{2}}
            \dot{\theta}{}_{1}^{2}\sin{\theta}_{2}
    - \dfrac{{c}_{2}}
            {{m}_{2}{L}_{1}{l}_{2}}
      \dfrac{\dot{\theta}_{2}}
            {\cos{\theta}_{2}}
    + {\alpha}_{1}\dot{\theta}_{1} - {\beta}_{1}v
    = {k}_{\rm sw}\dot{\theta}_{2}\cos{\theta}_{2}
    \\
    & \Longrightarrow\quad
    \dfrac{{\alpha}_{2}}{{L}_{1}}
            \dot{\theta}{}_{1}^{2}\sin{\theta}_{2}
    - \dfrac{{\beta}_{2}}
            {{L}_{1}}
      \dfrac{\dot{\theta}_{2}}
            {\cos{\theta}_{2}}
   + {\alpha}_{1}\dot{\theta}_{1} - {\beta}_{1}v
    = {k}_{\rm sw}\dot{\theta}_{2}\cos{\theta}_{2}
    \\
    & \Longrightarrow\quad
    v = \dfrac{1}{{\beta}_{1}}\biggl(
            {\alpha}_{1}\dot{\theta}_{1}
            - {k}_{\rm sw}\dot{\theta}_{2}\cos{\theta}_{2}
            + \dfrac{{\alpha}_{2}}{{L}_{1}}
                \dot{\theta}{}_{1}^{2}\sin{\theta}_{2}
            - \dfrac{{\beta}_{2}}
                    {{L}_{1}}
              \dfrac{\dot{\theta}_{2}}
                    {\cos{\theta}_{2}}
        \biggr)
    \tag{A.9}
\end{align}

のように得られます．ただし，

\begin{align}
    {\alpha}_{2} = \dfrac{{J}_{2}}{{m}_{2}{l}_{2}},\ 
    {\beta}_{2} = \dfrac{{c}_{2}}{{m}_{2}{l}_{2}}
\end{align}

であり，$\theta_2 \neq \pm \pi/2$ とします．

注意
$\cos{\theta}_{2} \neq 0$ である，すなわち，$\theta_2 \neq \pm \pi/2$（振子が左右水平ではない）としていますが，本記事で説明するように，振子が左右水平の付近にあるときは，無制御としますので，気にしないでください．

　最後に，振り上げ制御では，振子が真下にある状態から開始しますので，振子の基準角を真下からの変位 $\phi_2$ に変換します．そのために，$\rm (A.9)$ 式において，$\theta_2 = \phi_2 + \pi$ とすると，振り上げコントローラ

\begin{align}
    v = \dfrac{1}{{\beta}_{1}}\biggl(
            {\alpha}_{1}\dot{\theta}_{1}
            + {k}_{\rm sw}\dot{\phi}_{2}\cos{\phi}_{2}
            - \dfrac{{\alpha}_{2}}{{L}_{1}}
                \dot{\theta}{}_{1}^{2}\sin{\phi}_{2}
            + \dfrac{{\beta}_{2}}
                    {{L}_{1}}
              \dfrac{\dot{\phi}_{2}}
                    {\cos{\phi}_{2}}
        \biggr)
    \tag{A.10}
\end{align}

が得られます．ただし，$\phi_2 \neq \pm \pi/2$ です．
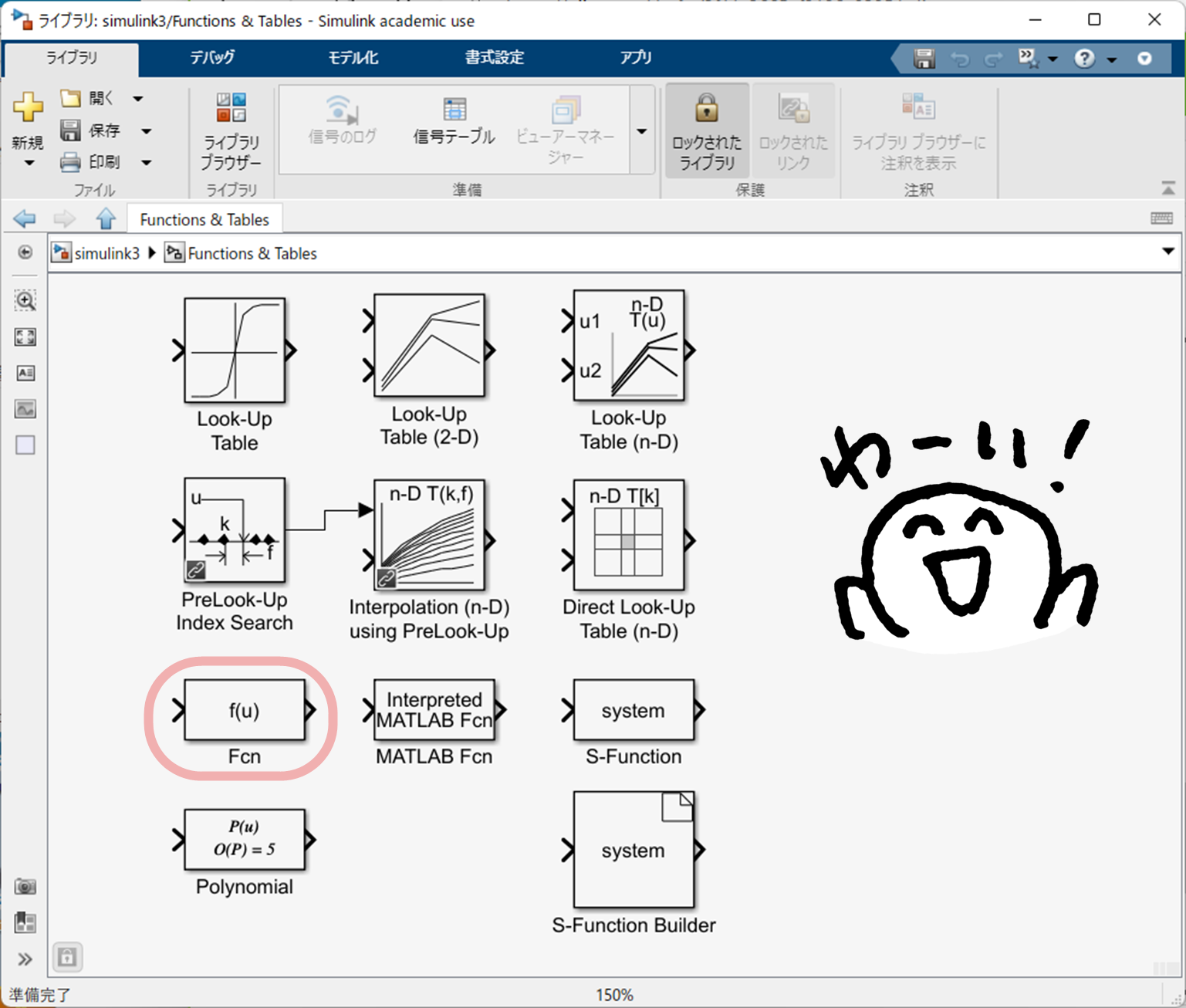
image.png

付録 B　R2020b から R2022b の場合の Simulink ブロック "Fcn" の利用

　"Fcn" は R2020b から R2022b では標準のライブラリから削除されていますので（R2023a から復活しました！），以下の手順で利用してください．
　MATLAB のコマンドウィンドウで

>> simulink3

と入力をして，以下の Simulink Block Library 5.0 を起動してください．
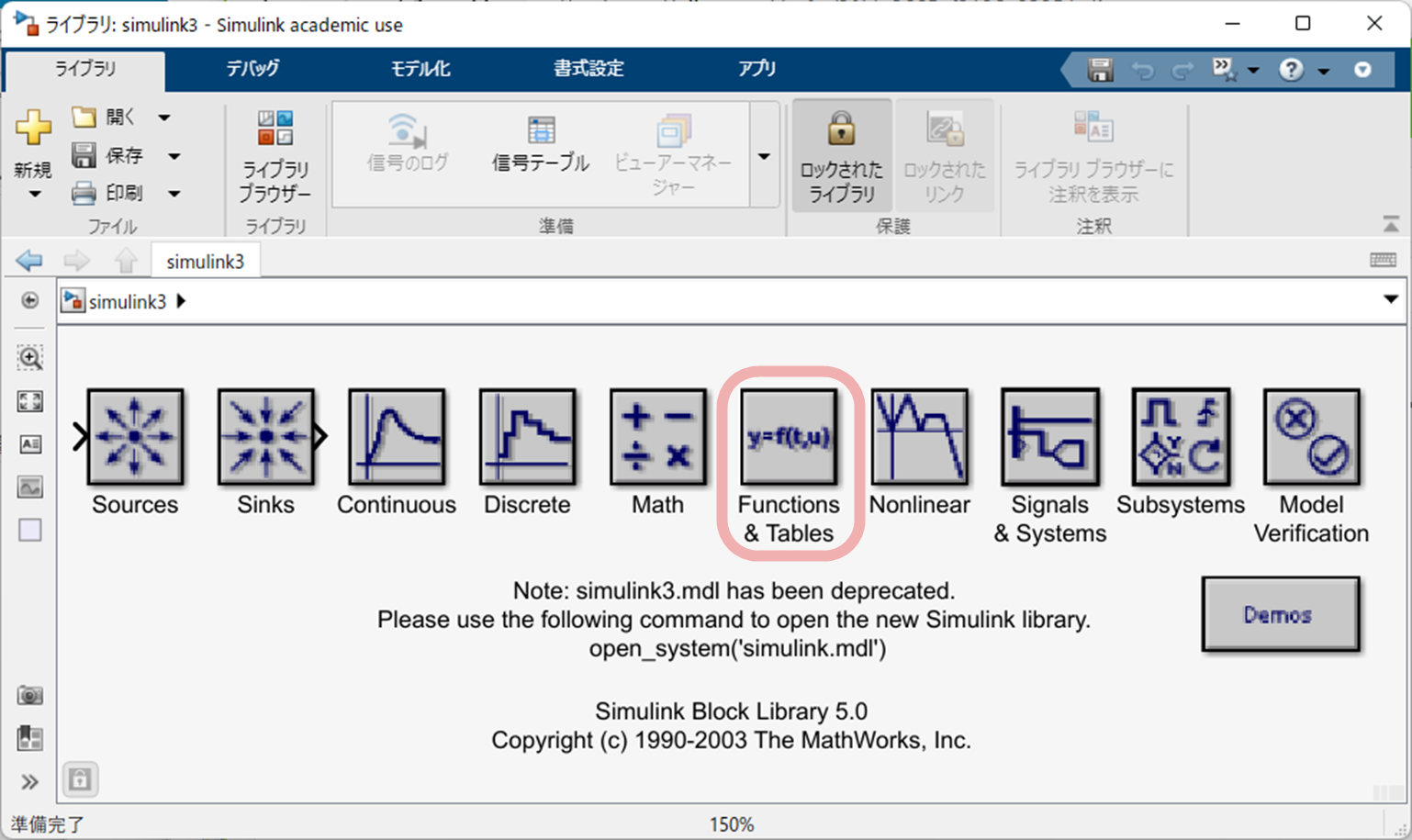
image.png
そして，ライブラリ "Functions & Tables" のなかから "Fcn" を "If Action Subsystem" にコピーしてください．
image.png

11
5
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
11
5