この記事は EAGLYS Advent Calendar 2022 の18日目の記事です
はじめに
TFHEに触れ始めてから1年弱経ったこともあり,人に聞かれることも増え始めてきたこの頃,今回のアドカレでTFHE関連の話題を予備知識なしの状態から始めて,詳細までまとめようと思います
突貫で書いてしまった部分もあるので,大いに誤りを含む可能性があります.誤字・脱字レベルでも構いませんので,ご指摘ください.
また,予告なしに内容の加筆や構成の変更を行うことがありますが,読みやすくするためのものですので,ご容赦ください
今回のアドカレの関連記事(気になるところから読んでください)
TFHEの概要
1日目:Torus・TLWEの概要
5日目:TRLWE・TFHEの概要
10日目:プログラマブルブートストラップの概要
TFHEの詳細
11日目:TFHEの暗号化方式の詳細(前半)
12日目:TFHEの暗号化方式の詳細(後半)
18日目(イマココ)(プログラマブルブートストラップの詳細(前半)):
19日目(プログラマブルブートストラップの詳細(後半)):
multi-key TFHEの概要
15日目(multi-key TFHEの概要):
TFHEの最新動向
20日目(TFHEの最新動向(理論編)):
25日目(TFHEの最新動向(実装編)):
今回はbootstrapの概要・Rescaling・Blind Rotation・Sample Extractionを扱います.
Key Exchange・bootstrapのまとめ・programmable bootstrapは次回扱います.
はじめに
この記事は,昨年のアドカレの記事
「プログラマブルブートストラップの原著論文を理解する回」を理解する回 4/4
のリメイク版となります.
分かりづらかった箇所の修正を行なったり,構成を入れ替えたり,そのとき書けなかった話を加えています
*具体例とか修正がない箇所もありますが,それはその都度明示します
1/4, 2/4 の記事は基本的に修正しません(と言っても今回の記事で一部リメイクします)が,それらの記事のサマリーは概要と称して,今回の1,5日目に載せていますので,そちらをご参照ください
bootstrapの概要
bootstrap の概要は今回の10日目の記事 プログラマブルブートストラップの概要を整理する
で書いたとおりです
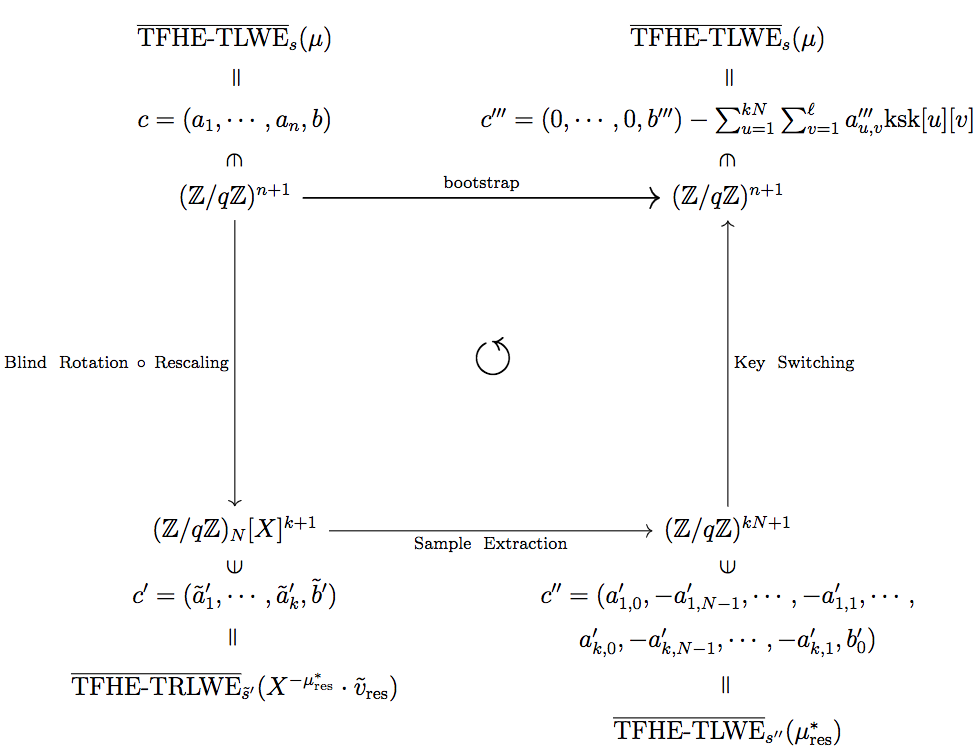
bootstrap は Rescaling, Blind Rotaion, Sample Extraction, Key Exchange の順で合成される関数で,暗号文のノイズを取り除く役割があります
リメイク元の記事でも載せましたが,bootstrap を構成する図式を↓に載せておきます
以下では,Rescaling, Blind Rotation, Sample Extraction, Key Switching の順に見ていきます
特にbootstrapを回したときにどこで時間がかかるのか,つまり,どのアルゴリズムで計算量が多いのかという点に注目していきます
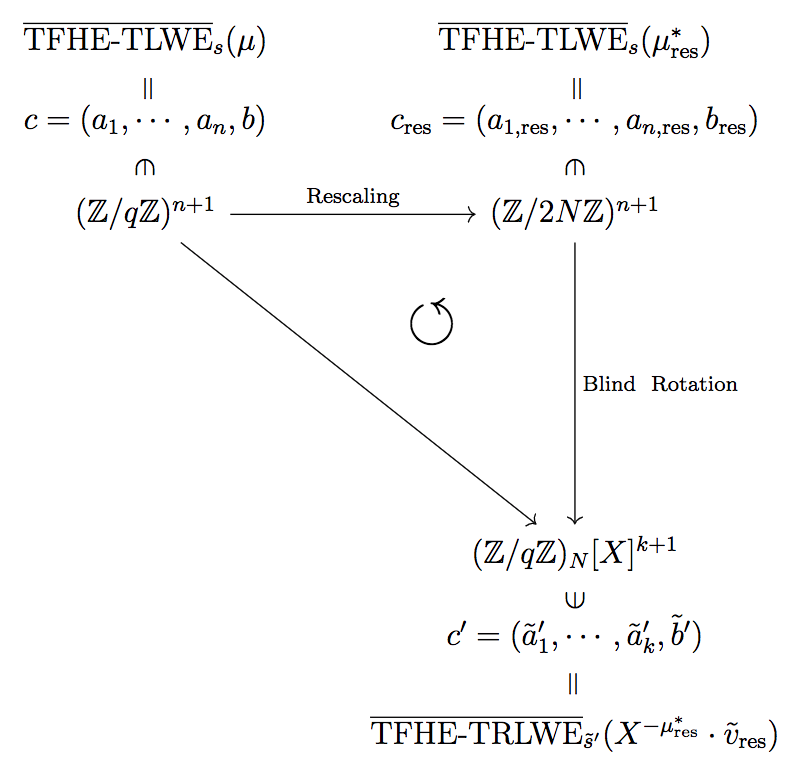
Rescaling
Blind Rotation 用に多項式の係数を調整します
2, 4, 6行目と同等の操作が全部で $n + N + 1$ 回だけ行われて,1回で $\mathbb{Z} / q \mathbb{Z}$ での掛け算が3回(割り算も掛け算とみなしています)なので,全体で
- $\mathbb{Z} / q \mathbb{Z}$ での掛け算 : $3(n + N + 1)$ 回
Blind Rotation
bootstrap のメインとなる箇所
GGSW方式の計算量は 前回の記事 より
- $\mathbb{Z} / q \mathbb{Z}$ での足し算 : $(k + 1) \ell((k + 1)N^2 + (n + 1)N + (k + 1))$ 回
- $\mathbb{Z} / q \mathbb{Z}$ での掛け算 : $(k + 1) \ell (n + k + 1) N^2$ 回
でしたから,さらにこれを$n$回だけ繰り返します
CMuxは所詮はif文なので,計算量は考えなくていいですが,$X^{a_{i, \mathrm{res}}} \cdot ACC$ の部分は,結局 $a_{i, \mathrm{res}} - b_{\mathrm{res}}$ の足し算を行なっています
つまり,最悪の場合,$\mathbb{Z} / q \mathbb{Z}$ での足し算を $n$ 回行います
よって,Blind Rotation の最悪計算量は,
- $\mathbb{Z} / q \mathbb{Z}$ での足し算 : $(k + 1) n \ell((k + 1)N^2 + (n + 1)N + (k + 1)) + n$ 回
- $\mathbb{Z} / q \mathbb{Z}$ での掛け算 : $(k + 1) n \ell (n + k + 1) N^2$ 回
Sample Extraction
Blind Rotation で長くなってしまった(サイズが増えてしまった)多項式をもう一度ベクトルの形に戻します
9行目で符号を入れ替える以外は計算量に特に影響しません
よって,Sample Extration の計算量は,
- $\mathbb{Z} / q \mathbb{Z}$ での掛け算 : $k(N - 1)$ 回
まとめ
前回の記事でGGSW方式はかなり計算量が多いことを確認しましたが,Blind Rotation はそれをさらにループさせているので,かなり計算時間がかかることが理論的にもわかります
ですので,bootstrap 全体の計算量を減らそうと思うと,真っ先に Blind Rotation の部分を変更すればいいと考えられます
実際,Blind Rotation に関する最適化の研究もいくつか知られているため,興味のある方はいくつか読んでみるのはいかがでしょうか?(僕もいずれまとめます)
今回の内容はここまでです.ここまでご覧になってくださった方々ありがとうございます!