この記事は EAGLYS Advent Calendar 2022 の11日目の記事です
はじめに
TFHEに触れ始めてから1年弱経ったこともあり,人に聞かれることも増え始めてきたこの頃,今回のアドカレでTFHE関連の話題を予備知識なしの状態から始めて,詳細までまとめようと思います
突貫で書いてしまった部分もあるので,大いに誤りを含む可能性があります.誤字・脱字レベルでも構いませんので,ご指摘ください.
また,予告なしに内容の加筆や構成の変更を行うことがありますが,読みやすくするためのものですので,ご容赦ください
今回のアドカレの関連記事(気になるところから読んでください)
TFHEの概要
1日目:Torus・TLWEの概要
5日目:TRLWE・TFHEの概要
10日目:プログラマブルブートストラップの概要
TFHEの詳細
11日目(イマココ)(TFHEの暗号化方式の詳細(前半)):
12日目(TFHEの暗号化方式の詳細(後半)):
18日目(プログラマブルブートストラップの詳細(前半)):
19日目(プログラマブルブートストラップの詳細(後半)):
multi-key TFHEの概要
15日目(multi-key TFHEの概要):
TFHEの最新動向
20日目(TFHEの最新動向(理論編)):
25日目(TFHEの最新動向(実装編)):
今回はTFHE方式とそれに関わる暗号文の演算を扱います.
GGSW方式やそれに関わる暗号文への演算は次回扱います.
はじめに
この記事は,昨年のアドカレの記事
「プログラマブルブートストラップの原著論文を理解する回」を理解する回 3/4
のリメイク版となります.
分かりづらかった箇所の修正を行なったり,構成を入れ替えたり,そのとき書けなかった話を加えています
*具体例とか修正がない箇所もありますが,それはその都度明示します
1/4, 2/4 の記事は基本的に修正しません(と言っても今回の記事で一部リメイクします)が,それらの記事のサマリーは概要と称して,今回の1,5日目に載せていますので,そちらをご参照ください
Discretized Torus
*Torus の概要については Torus・TLWEの概要 をご参照ください
Torus とは,大雑把には,0以上1未満の実数全体の集合とみなすことができるのでした
つまり,Torusは無限集合なわけです
無限集合を計算機上で表すことはできないので,離散化する必要があります
Torusの離散化として,今回は $q$ を2べきとしたとき,$q^{-1} \mathbb{Z} / \mathbb{Z}$ で表します
*大雑把には $q^{-1} \mathbb{Z} / \mathbb{Z} =${$0, \frac{1}{q}, \cdots, \frac{q - 1}{q}$} で足し算とスカラー倍ができる集合です,厳密には右辺の各要素を代表元とする同値類
このとき,$\hat{T} = q^{-1} \mathbb{Z} / \mathbb{Z}$ とします.
平文
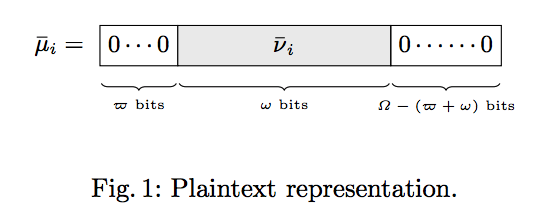
ここでいう平文とは,plaintext のことで,生データを cleartext で表します.
つまり,cleartext を「加工」したものを plaintext と呼ぶのですが,ここで,plaintext とは↓のような構造をしています
*上記は,I. Chillotti, M. Joye, P. Paillier: ``Programmable bootstrapping enables efficient homomorphic inference of deep neural networks'', In: International Symposium on Cyber Security Cryptography and Machine Learning, Springer, Cham, pp. 1-19, 2021.
の4ページ記載のFig1 をスクショしたものです
つまり,先頭ビットから
- $\bar{\omega}$ bit : 準同型暗号での先頭パディング用
- $w$ bit : cleartext の情報格納用
- $\Omega - (\bar{\omega} + \omega)$ bit : ノイズ格納用
のような形になっています
リメイク前の訂正
リメイク前の 「プログラマブルブートストラップの原著論文を理解する回」を理解する回 2/4「Upper」 では
- $\bar{\omega}$ bit : 準同型暗号での先頭パディング用
- $w$ bit : cleartext の情報格納用
- 1 bit : 0が入る
- $\Omega - (\bar{\omega} + \omega + 1)$ bit : ノイズ格納用
としていましたが,後述するように演算回数の指定を変えることで,cleatext 後の 1 bit は不要となります
暗号文でもこの形式となっています
準同型暗号を考えているので,後で暗号文の足し算やスカラー倍などを考えます
すると,足し算をすればするほど,ノイズ格納用に格納されるノイズが増えます
ノイズ格納用 bit は有限ですから,何も考えずに足し算を行うと,ノイズが溢れてしまいます
ノイズ部分での計算が cleartext の部分に影響して,その結果復号すると異なる演算結果となるのは非常に困る事態です
1つの解決策として,暗号文に対する演算回数を事前に指定しておく,というものがあります(これを leveled operation といいます)
例えば,TLWE問題やTRLWE問題で生成されるノイズが 2 bit 以下で,今回のノイズ格納用 bit が 4 bit の場合,演算回数を4回までと指定することで,ノイズが溢れるのを防ぐことができます
なお,平文から cleatext の情報を抜き出すには,Upper関数を使うのでした
*Upper関数については 「プログラマブルブートストラップの原著論文を理解する回」を理解する回 2/4「Upper」 をご参照を
TFHE方式
TFHE 方式に関しては,5日目の TRLWE・TFHEの概要を整理する でも触れましたが,実は TFHE-TLWE 方式と TFHE-TRLWE 方式の2種類があり,ここではTorusの離散化・平文の構造に対応したバージョンで紹介します
TFHE-TLWE
まずは,TFHE-TLWE方式から
こちらは,TLWE問題をもとにしています
Encの部分をより具体的に擬似コードで書いたものが次です:
計算量的な話をすると,4行目が効いていて
- $\mathbb{Z} / q \mathbb{Z}$ での足し算 : $n + 1$ 回
- $\mathbb{Z} / q \mathbb{Z}$ での掛け算 : $n$ 回
です
TFHE-TRLWE
続いて,TFHE-TRLWE方式です
こちらは,TRLWE問題をもとにしているので,多項式を扱います
Encの部分をより具体的に擬似コードで書いたものが次です:
こちらも計算量的な話として,7行目で
- $\mathbb{Z} / q \mathbb{Z}$ での足し算 : $(n + 1)N$ 回
- $\mathbb{Z} / q \mathbb{Z}$ での掛け算 : $n N^2$ 回
です
長さが $N$ (次数が $N - 1$) の多項式というのは,$N$ 次元ベクトルとみなせますから,実質,TFHE-TLWE方式を $N$ 回繰り返しているのと同じですので,基本的に計算回数は TFHE-TLWE での $N$ 倍になります
しかし,掛け算では $N^2$ 倍になっているのは,多項式の掛け算由来です(長さが $N$ の多項式同士の掛け算では合計で $N^2$ 回の掛け算を行うため)
*「プログラマブルブートストラップの原著論文を理解する回」を理解する回 3/4 での「TFHE方式のアルゴリズムの具体例」は今回扱いません
今回の内容はここまでです.ここまでご覧になってくださった方々ありがとうございます!