この記事はEAGLYS Advent Calendar 2021の10日目の記事です。

今回の記事は下記の記事からの続きとなります．

プログラマブルブートストラップの原著論文の第２〜４章を厳密に考察します．
全体を通して使う記号や前提知識などは第１回目の記事にまとめています．

突貫で書いてしまった部分もあるので，大いに誤りを含む可能性があります．誤字・脱字レベルでも構いませんので，ご指摘ください．
また，予告なしに内容の加筆や構成の変更を行うことがありますが，読みやすくするためのものですので，ご容赦ください

全４回通しでの目次

第１回

本論文全体の流れ
前提知識
2.1 Torus and Torus Polynomials
- Torus
- 加群
- 多項式環
- 既約多項式と円分多項式
- Torus上の多項式
2.2 Probability Distributions
- 離散一様分布と正規分布
- 実数から整数への丸め

第２回（イマココ）

Appendix A : Complexity Assumptions Over the Real Torus
- TLWEとTRLWE
3章前説
- 3章の流れ
- ギリシャ文字と花文字
- $\hat{\mathbb{Z}}$ と $\hat{\mathbb{T}}$
- 3章前説の議論
3.1 Encoding/Decoding Messages
- lift
- Upper
- 3.1の議論

第３回

第４回

今回は第２回目で，
Appendix A : Complexity Assumptions Over the Real Torus
3 Discretized TFHE
3.1 Encoding/Decoding Messages
を扱います．

具体的な内容としては，次のようになります:

Appendix A : Complexity Assumptions Over the Real Torus
- TLWEとTRLWE
3章前説
- ギリシャ文字と花文字
- $\hat{\mathbb{Z}}$ と $\hat{\mathbb{T}}$
- 3章前説の議論
3.1 Encoding/Decoding Messages
- lift
- Upper
- 3.1前説の議論

ちなみに次回からが本番って感じです．前回と今回は論文の理解としては楽なので，数学的な補足を多めにしています．
論文中の議論をどのように解説するかは，今回の「3章前説の議論」に記載しています．
それでは早速見ていきましょう．

TLWEとTRLWE

＊はじめはここのタイトルを論文に合わせて「LWEとGLWE」にしていたのですが，変更することにしました．
Torus上のLWE問題なのでTLWE，Torus上の多項式環ベースのLWE問題なのでTRLWEとします．影響がある部分は全て変更しています．

格子暗号が基づくNP困難な問題として，Torus 上のLWEとそれを多項式環へ拡張したTorus上のRLWEを紹介します．

$\underline{\mathrm{TLWE問題}}$
$n \in \mathbb{N}, \ s = (s_1, s_2, \cdots, s_n) \overset{\$}{\leftarrow} \mathbb{B}^n$ とする．また，$\mathcal{X}$ を $\mathbb{R}$ 上の正規分布とする．
このとき，Torus上のLWE問題と（TLWE問題）は次の2つの分布を識別することである:

\begin{align*}
\displaystyle

\tilde{D}_0 & = \{ (a, r) \ | \ a = (a_1, a_2, \cdots, a_n) \overset{\$}{\leftarrow} \mathbb{T}^n, \ r \overset{\$}{\leftarrow} \mathbb{T} \} \\
\tilde{D}_1 & = \{ (a, r) \ | \ a = (a_1, a_2, \cdots, a_n) \overset{\$}{\leftarrow} \mathbb{T}^n, e \overset{\$}{\leftarrow} \mathcal{X}, \ r = \sum_{j = 1}^n s_j \cdot a_j + e \}

\end{align*}

$\underline{\mathrm{TRLWE問題}}$
$N, k \in \mathbb{N}$ で $N$ を2べきとする． $\tilde{s} = (\tilde{s}_1, \cdots,\tilde{s}_k) \overset{\$}{\leftarrow} \mathbb{B}_N[X]^K$ とする．また，$\mathcal{X}$ を $\mathbb{R}$ 上の正規分布とする．
このとき，Torus上のRLWE問題（TRLWE問題）とは次の2つの分布を識別することである:

\begin{align*}
\displaystyle

\tilde{D}_0 & = \{ (\tilde{a}, \tilde{r}) \ | \ \tilde{a} = (\tilde{a}_1, \tilde{a}_2, \cdots, \tilde{a}_n) \overset{\$}{\leftarrow} \mathbb{T}[X]^n, \ \tilde{r} \overset{\$}{\leftarrow} \mathbb{T}[X] \} \\
\tilde{D}_1 & = \{ (\tilde{a}, \tilde{r}) \ | \ \tilde{a} = (\tilde{a}_1, \tilde{a}_2, \cdots, \tilde{a}_n) \overset{\$}{\leftarrow} \mathbb{T}[X]^n, \tilde{e} \overset{\$}{\leftarrow} \mathcal{X}, \ \tilde{r} = \sum_{j = 1}^n \tilde{s}_j \cdot \tilde{a}_j + \tilde{e} \}

\end{align*}

＊論文と記号が対応していない箇所がありますが，今回の「ギリシャ文字と花文字」で補足します

一見すると，仰々しいかもしれませんが，TLWEさえ理解できれば，TRLWEは範囲を多項式環に拡張しただけ，と分かります．

TLWEは大雑把にいうと，$a, r$ が与えられたときに，誤差 $e$ が生じる状況で $\displaystyle r = \sum_{j = 1}^n s_j \cdot a_j + e$ から $s$ を求める，という問題です．
設定から分かるように，機械学習由来の問題です．この $s$ を求める部分が（$s$ のビット長をオーダーとした）NP困難な問題です．

$s$ が簡単に分かってしまうと識別できてしまいます．つまり，$s$ を簡単に求めるのは難しい，ということです．
今回では，ノイズ $e$ が効いています．もしノイズがないと単なる連立方程式を解けばいい，となるので，$s$ が分かってしまいます．
しかし，真の値 $r$ にノイズが加わることで，一気にその連立方程式を解くのが難しくなります．

上記の説明は下記の書籍を参考にしました．聖書なので素晴らしいですね．
耐量子計算機暗号

3章の流れ

ここから３章です．
３章ではTFHE方式の一般論と Leveled operation について触れます．具体的には次のようになります．
前説：TLWEを使った暗号化
3.1：メッセージの暗号化
3.2：THFE方式の暗号化アルゴリズム
3.3：leveled operation
前説と3.1は3.2のためにあって，3.3では3.2で定義した暗号文に対しての演算を考えています．

ギリシャ文字と花文字

よくある問題として

議論の際に文字足りないがち

という問題がどの分野でも往々にしてあります（たぶん）．
例えばすでに $m$ という記号を使っていたり似たような意味で使いたい場合，$m'$ とか $\tilde{m}$ とか $M$ とか $\hat{m}$ とか色々な方法があります．
ただし，これでは限界があり，アルファベット以外の表音文字に頼ることがあります．よく使うのがギリシャ文字と花文字です．

見慣れない文字のせいで変に議論が難しく見えてしまうこともあります．そこで，ここでは今回の論文に出てくるギリシャ文字・花文字とアルファベットの対応をまとめました．
なんかよく分からん文字が出てきたなと思ったら，ここに立ち返ってみてください．

そして，今回の「LWEとGLWE」で触れた補足をします．
この論文中では，「花文字の小文字」を使用しています．が，それをTeXで出力する方法が分からんのです・・・（大文字なら分かるんですけどねぇ・・・）．
よって，花文字の一覧は下記に提示しますが，この記事では（大文字も）「アルファベットにチルダを付けたもので代用」とします．上の出力方法が分かれば，良い感じにリメイクします．

アルファベット	ギリシャ文字	花文字	花文字の代わり
a	$\alpha$	𝒶	$\tilde{a}$
e	$\epsilon$	ℯ	$\tilde{e}$
r	$\rho$	𝓇	$\tilde{r}$
s	$\sigma$	𝓈	$\tilde{s}$
D	$\Delta$	$\mathscr{D}$	$\tilde{D}$
M	Μ	$\mathscr{M}$	$\tilde{M}$
N	Ν	$\mathscr{N}$	$\tilde{N}$
O	$\Omega$	$\mathscr{O}$	$\tilde{O}$
U	$\Sigma$	$\mathscr{U}$	$\tilde{U}$

花文字の小文字はこちらのサイトからコピペしました

hatについて

上ででてきた「似たような意味で使いたい」場合の例になっています．
$\hat{\mathbb{T}}$ と $\hat{\mathbb{Z}}$ を定義します．

以下では $q$ を2べきの自然数とします．

$\underline{\mathrm{Def(\hat{\mathbb{T}}, \hat{\mathbb{Z}})}}$
$q$ を2べきの自然数として，$\hat{\mathbb{T}} = q^{-1} \mathbb{Z} / \mathbb{Z}, \ \hat{\mathbb{Z}} = \mathbb{Z} / q \mathbb{Z}$ と定める．

具体的な元を書いておくと，

\displaystyle
\begin{align*}
\hat{\mathbb{T}} &= q^{-1} \mathbb{Z} / \mathbb{Z} = \left \{ 0 + n, \frac{1}{q} + n, \frac{2}{q} + n, \cdots, \frac{q - 1}{q} + n \right \} \\
\hat{\mathbb{Z}} &= \mathbb{Z} / q \mathbb{Z} = \left \{ 0 + nq, 1 + nq, 2 + nq, \cdots, q - 1 + nq \right \}
\end{align*}

です．

なぜ $q$ が2べきなのか，なぜ $\hat{\mathbb{T}}$ や $\hat{\mathbb{Z}}$ を導入する必要があるのか，については今回の「3章前説の議論」の最後の太字で解説しています．

これらは体ではありません（$q$ が素数ではないため）．
また，$\hat{\mathbb{T}}$ 内では掛け算は定義されません．分母の $q$ の指数は1のみ許されていますが，掛け算をすると，指数が2以上になるためです．

また，僕が書く記事は $\mathbb{Z} / p \mathbb{Z}$ のことを $\mathbb{Z}_p$ と表記することはなく，$\mathbb{Z} / p \mathbb{Z}$ できっちり書くか，$\mathbb{F}_p$ と書きます（$p$ 進整数環というものと記号がバッティングするため）．

これらの多項式環は次のようにかけます．

$\underline{\mathrm{Def(\hat{\mathbb{T}}_N[X], \hat{\mathbb{Z}}_N[X])}}$
$q$ を2べきの自然数で $N$ を自然数として，

\begin{align*}
\hat{\mathbb{T}}_N[X] &= \hat{\mathbb{T}}[X] / (X^N + 1) = (q^{-1} \mathbb{Z} / \mathbb{Z})[X] / (X^N + 1) \\
\hat{\mathbb{Z}}_N[X] &= \hat{\mathbb{Z}}[X] / (X^N + 1) = (\mathbb{Z} / q \mathbb{Z})[X] / (X^N + 1)
\end{align*}

と定める．

$\mathbb{T}$ は

和でAbel群
整数のスカラー倍を考えられる

と同様に，$\mathbb{T}_N[X]$ は

和でAbel群
整数のスカラー倍を考えられる

と同様に，$\hat{\mathbb{T}}_N[X]$ は

和でAbel群
整数のスカラー倍を考えられる

ことに注意しましょう．

さてここから議論の流れが少し変わります．
これからは $\hat{\mathbb{T}}$ を扱っていく・・・んですが，$\hat{\mathbb{T}}$ と $\hat{\mathbb{Z}}$ の元を見比べてください．各元を $q$ 倍しただけしか違いがありません．

よって，$\hat{\mathbb{T}}$ を扱っていく代わりに今後はより扱いやすい，$\hat{\mathbb{Z}}$ で考えていくことになります．

流れをまとめると，
始めは Torus $\mathbb{T}$ を考えていた
$\rightarrow$ Torus の元１つだけでなく，多項式（ベクトル）として $\mathbb{T}[X]$ で考える
$\rightarrow$ 計算機上で扱えるように多項式の長さを制限すべく $\mathbb{T}_N[X]$ で考える
$\rightarrow$ 計算機上で扱えるように多項式の長さを制限すべく $\hat{\mathbb{T}}_N[X]$ で考える
$\rightarrow$ 更に扱いやすくするために，$\hat{\mathbb{Z}}_N[X]$ で考える
という感じです．

そして，$\hat{\mathbb{T}}_N[X]$ では定義できなかった掛け算が，$\hat{\mathbb{Z}}_N[X]$ では定義できるようになる，というのが後々で効いてきます．が，この辺は第３回の話です．

3章前説の議論

さて，ここからが本番なのですが，議論をただ追うのは理解したことにならない（数学科っぽいこと言ってる）ので，個人的には「イメージ」を「式」で厳密にする感覚で進めます（もちろん全部が全部そうできるわけではないですが）．

TLWE問題とはNP困難な問題でした．暗号理論では，NP困難な問題を背景に暗号方式が作られます．
重要なことは，$a$ と $r$ が分かっても，$s$ は簡単には分からないことです．

TLWEを振り返ってみると

自然数 $n$ が与えられて，$s = (s_1, s_2, \cdots, s_n) \in \mathbb{B}^n$ を秘密鍵として，$r \in \mathbb{T}, \ a = (a_1, a_2, \cdots, a_n) \in \mathbb{T}^n$ とノイズ $e$ が与えられたときに，$\displaystyle r = \sum_{j = 1}^n s_j \cdot a_j + e$　なる $s$ を求めるのが難しい

ということでした．

実際の暗号化では，$\mu \in \mathbb{T}$ なる平文に対して，$a$ と $r + \mu$ を送信します．論文では，$a = (a_1, a_2, \cdots, a_n) \in \mathbb{T}^n$ と $\mathbb{T}$ が和で閉じていることから $\mu + r \in \mathbb{T}$ なので，これらの組として，$c = (a_1, a_2, \cdots, a_n, \mu + r)\in \mathbb{T}^{n + 1}$ を暗号文を送信します．

以上がTLWEについてです．
そして，TRLWEへの拡張としては，TRLWEはTLWEの実数部分を実数多項式へ拡張すればいいのでした．TRLWEも同じように考えられます．

Torus上かどうかに限らずLWEからGLWEへの拡張は毎回こんなテンションです．

しかしここでよく考えたいこととして，

$\mathbb{T}$ の任意の元って計算機上で表せるの？

ということです．$\mathbb{T}$ は0以上1未満の実数全体の集合ですので，無限集合になります．

先にこちらの問いを考えてみましょう．

$\mathbb{Z}$ の任意の元って計算機上で表せるの？

これは無理です．そもそも計算機上で表せる数には限界があるからです．よって， 32bit なり 64bit 精度で以下は考えることにしましょう．
すると，$\Omega (= 32, 64)$ bit 精度では，0以上 $q - 1$ ($q = 2^{\Omega}$) までの全ての整数を表せます．そして，この範囲の整数は $\mathrm{mod} \ q$ での足し算と掛け算を考えることで，$\mathbb{Z} / q \mathbb{Z}$ 内で考えれば良いことになります．$\mathbb{Z} / q \mathbb{Z}$ を $\hat{\mathbb{Z}}$ と書くわけです．

つまり，「$\mathbb{Z}$ の任意の元は計算機上で表せない」ですが，「$\mathbb{Z} / q \mathbb{Z}$ の任意の元は計算機上で表せる」ということになります．

0以上 $q - 1$ までの全ての整数を実現できるのなら，$\cfrac{1}{q}$ 刻みで0以上 $\cfrac{q - 1}{q}$ までの全ての有理数を実現できる，と考えるのは自然ではないでしょうか．

そこで出てくるのが $\hat{\mathbb{T}}$ になります．

以上をまとめると，理論的には $\mathbb{Z}$ や $\mathbb{T}$ で考えればよかったものを，計算機上で扱うために $\hat{\mathbb{Z}}$ や $\hat{\mathbb{T}}$ で置き換えていきます． よって，本質的な議論が何か変わったわけではありません．
そして，これらの多項式環として，$\hat{\mathbb{T}}_N[X]$ や $\hat{\mathbb{Z}}_N[X]$ も考えていきます．

以上で３章前説の議論は終わりです．

lift

ここから3.1です．
「持ち上げ」関数についてです．定義域を拡張する関数と解釈できます．

$\underline{\mathrm{Def(lift \ function)}}$
$\overline{x} \in \mathbb{Z} / q \mathbb{Z}$ に対して，$\overline{x}$ に対応する代表元 $x \in [0, q)$ を取る．このとき，lift関数を次のように定める:

$$\mathrm{lift} : \mathbb{Z} / q \mathbb{Z} \ni \overline{x} \mapsto x \in \mathbb{Z}$$

＊上記の定義では，論文中で定義されている lift 関数の定義をもう少し精密にしています

一見すると何もやっていない関数のように思えますが，後で $q$ で割ることを考えます．
すると $\mathbb{Z} / q \mathbb{Z}$ では0で割ることに対応してしまいますので，それを避けるために一旦定義域を広げる必要があります．

これはプログラム的には，例えば，

int a = 1;
long long b = pow(2, 11);
b += (long long)a;

みたいな感じです．long long 内での足し算を行うには，aの定義域を int から long long に一旦広げる必要があります．

Upper

続いてUpper関数についてです．

以下では $p, q$ を2べきで $2p \leq q$ とします．つまり，$p = 2^m, q = 2^n$ としたとき，$m + 1 \leq n$ です．
このとき，$x_H \in \mathbb{Z} / q \mathbb{Z}$ と $\displaystyle x_L \in \left [0, \frac{q}{2p} - 1 \right]$ を任意に取って，$x \in \mathbb{Z} / q \mathbb{Z}$ を $\displaystyle x = x_H \frac{q}{p} \pm x_L$ と表します．$\pm$ はどちらを選択してもいいとします．

Upper関数とは，上記の $x_H \frac{q}{p}$ を返す関数です．

$\underline{\mathrm{Def(Upper \ function)}}$
$x_H \in \mathbb{Z} / q \mathbb{Z}$ と $\displaystyle x_L \in \left[ 0, \frac{q}{2p} - 1 \right]$ を任意に取って，$x \in \mathbb{Z} / q \mathbb{Z}$ を $\displaystyle x = x_H \frac{q}{p} \pm x_L$ とする．
このとき，Upper 関数を次のように定める:

\begin{align*}
\displaystyle
\mathrm{Upper}_{q, p} : \mathbb{Z} / q \mathbb{Z} \ni x \mapsto \frac{q}{p} \left \lfloor \frac{p \ \mathrm{lift}(x)}{q} \right \rceil \in \mathbb{Z} / q \mathbb{Z}
\end{align*}

＊論文中では $x_L$ の定義域は $0 \leq x_L \leq \frac{q}{2p}$ ですが，上記では $0 \leq x_L \leq \frac{q}{2p} - 1$ に訂正しています．

定義から，0以上 $q - 1$ 以下の整数を $\frac{q}{p}$ の倍数に返す関数と思えます．

何が「Upper」ぽいのかと$x_L$ の定義域が $[0, \frac{q}{2p} - 1]$ であるもう少しダイレクトな理由は，同じく今回の「3.1の議論」のデコード太字部で解説しています．

3.1の議論

最後に cleartext から plaintext への変換の話を紹介して今回は終了します．
ここでは一旦 TLWE や TRLWE のことは忘れてください．

cleartext と plaintext について
エンコードとデコードの関係
エンコード
デコード
エンコードとデコードの具体例

の順で説明します．
以下，自然数 $N, w, \Omega, \bar{w}$ を固定します．

cleartext と plaintext について
まず，cleartext と plaintext の2つについて説明します．
cleartext とは，俗にいうメッセージのことです．plaintext は「暗号化アルゴリズム」の input のことです．イメージとしては，cleartext が実際の文章で，plaintext が bit 文字列とか思うといいかと（実際には下記のようにもっと色々やりますが）．
ここでは cleartext から plaintext へのエンコードとデコードを説明します．

＊エンコードは変に和訳しないで，エンコードと表現することにします．「暗号化」と言ったら，3.2 での plaintext から ciphertext への変換のことを指すことにします．

エンコードとデコードの関係
上記のエンコードとデコードではどのような関係があるかというと，任意の cleartext $m$ に対して（定義域は後で正当化），エンコードアルゴリズム Encode とデコードアルゴリズム Decode があって，$\mathrm{Decode(Encode(} m \mathrm{))} = m$ が成り立ちます．暗号化のアルゴリズムと同じですね．

エンコード
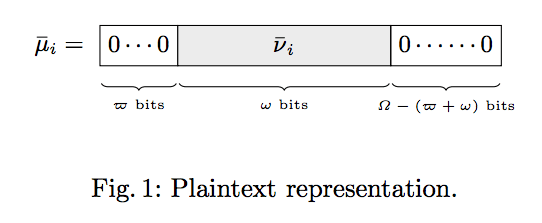
エンコードの結論を図解すると次のとおりです．

＊上記は，元の論文の4ページ記載のFig1 をスクショしたものです

それぞれのパラメタ $w, \ \bar{w}, \ \Omega - (\bar{w} + w)$ について説明します．
まず $\bar{w}$ です．
これは，準同型暗号では，plaintext の各係数 $\mu_i$ の先頭数ビットに0をパディングする必要があります．ここで必要な bit 長を $\bar{w}$ としています．

次に $w$ です．
これは cleartext を $m = (m_0, m_1, \cdots, m_{N - 1})$ の文字列で各係数 $m_i$ は $w$ bit 長としています．

最後に $\Omega - (\bar{w} + w)$ です．
まず，$\Omega$ について．
これは，各係数 $\mu_i$ は定義域が $\hat{\mathbb{Z}} = \mathbb{Z} / q \mathbb{Z} = \mathbb{Z} / 2^{\Omega} \mathbb{Z}$ であるような plaintext $\mu = \mu_0 + \mu_1 X + \cdots + \mu_{N - 1} X^{N - 1}$ を考えます．各係数の定義域は $\mathbb{Z} / 2^{\Omega} \mathbb{Z}$ なので $\Omega$ bit 長としています．
このときパラメタの間には $\bar{w} + w \leq \Omega$ が成り立っているものと仮定します．後ろの $\Omega - (\bar{w} + w)$ bit が余っていることに注意してください．

そして，後ろの余った $\Omega - (\bar{w} + w)$ bit についてです．
今回の「3章前説の議論」では，この plaintext に $\tilde{r}$ を加えるのでした．$r$ にはノイズ $\tilde{e}$ が含まれています．つまり，$\mu$ の各係数 $\mu_i \in \hat{\mathbb{Z}} = \mathbb{Z} / q \mathbb{Z}, \ q = 2^{\Omega}$ に対して，ノイズ $e_i$ が加わっている状況です．
ここでノイズを加える場所を後ろの余った $\Omega - (\bar{w} + w)$ bit としているわけです．
厳密には，後ろ $\Omega - (\bar{w} + w) - 1$ bit にノイズを挿入します

以上で cleartext から plaintext へのエンコードが終わりです．上記の図をもとに振り返ると，左から順に

先頭 $\bar{w}$ bit $\cdots$ パディング用
中央 $w$ bit $\cdots$ cleartext の情報格納用
調整用 $1$ bit $\cdots$ 0 が入る
後ろ $\Omega - (\bar{w} + w) - 1$ bit $\cdots$ ノイズ格納用

ということになります．

デコード
plaintext $x \in \mathbb{Z} / q \mathbb{Z}$ が与えられたとします．つまり $x$ は $\Omega$ bit 長です．
結論としては，$x$ に Upper 関数を作用させれば復号できます．
また，Upper 関数は $\Omega$ bit の文字列から先頭 $\bar{w} + w$ bit の情報を取り出すように定義されていて，先頭の情報を取り出す様子が「Upper っぽい」 ことも解説します．

このとき，ノイズ部分を除いた先頭の $\bar{w} + w$ bit 長の情報を取得できれば，$\bar{w}$ は分かっているので，先頭の $\bar{w}$ bit の0を取り除くことで，cleartext を復元できることになります．
では，どうやって $x$ から先頭 $\bar{w} + w$ bit 長を取得するかというと，そこで登場するのが Upper 関数です．

Upper 関数とは $x \in \mathbb{Z} / q \mathbb{Z}$ に対して $\displaystyle x = x_H \frac{q}{p} \pm x_L$ から $\displaystyle x_H \frac{q}{p}$ を返す関数のことでした．$q = 2^{\Omega}, \ p = 2^{\bar{w} + w}$ とすると，plaintext $x = x_H \frac{q}{p} \pm x_L$ から $\displaystyle x_H 2^{\Omega - (\bar{w} + w)}$ が返ってきます．

実は，この操作でノイズ部分を無視した先頭 $\bar{w} + w$ bit が返ってきます．
実際に計算すると分かりますが，ノイズを格納する $x_L$ の範囲が $[0, 2^{\Omega - (\bar{w} + w) - 1} - 1]$ であって，$[0, 2^{\Omega - (\bar{w} + w)} - 1]$ や $[0, 2^{\Omega - (\bar{w} + w) - 1}]$ でない理由は，Upper 関数の $\lfloor \cdot \rceil$ の中身がノイズの部分がちょうどうまく消えて，$x_H$ になるように調整されているため，ということです．

先ほども書きましたが，そこから先頭 $\bar{w}$ bit と後ろの $\Omega - (\bar{w} + w)$ bit（共に全て0）を取り除くと，無事に cleartext へ復号できました．

エンコードとデコードの具体例

では，エンコードとデコードの具体例を紹介して終わりにします．

以下では，$N = 4, \ w = 4, \ \Omega = 8, \bar{w} = 2$ とします．つまり，$p = 2^{\bar{w} + w} = 2^6 = 64, \ q = 2^{\Omega} = 256$ です．

このとき，cleartext $m = (m_0, m_1, m_2, m_3) \in (\mathbb{Z} / 2^w \mathbb{Z})^N = (\mathbb{Z} / 16 \mathbb{Z})^4$ として，$m_0 = 13, \ m_1 = 4, m_2 = 9, m_3 = 6$ とします．つまり，それぞれの bit 表現を順に $1101, \ 0100, \ 1001, \ 0110$ とします．

すると，plaintext $\mu \in (\mathbb{Z} / 2^{\Omega} \mathbb{Z})^N = (\mathbb{Z} / 256 \mathbb{Z})^4$ の各係数の bit 表現は $00110100, \ 00010000, \ 00100100, \ 00011000$ となって，これを10進数に直すと $\mu_0 = 52, \ \mu_1 = 16, \ \mu_2 = 36, \ \mu_3 = 24$ です．
確かに 2 bit だけ左シフトしているときに $\mu_0 = 4 m_0, \ \mu_1 = 4 m_1, \ \mu_2 = 4 m_2, \ \mu_3 = 4 m_3$ が成り立っています．

このとき，ノイズを考慮して，plaintext の各係数の後ろ1 bit に bit 反転が起こったり起こらなかったりを仮定します．
つまり， $\mu_0^{\prime}, \ \mu_1^{\prime}, \ \mu_2^{\prime}, \ \mu_3^{\prime}$ であって，bit 表現が $00110101, \ 00010000, \ 00100101, \ 00011001$ のように変換したとします．
すると，10進数に直したとき $\mu_0^{\prime} = 53, \ \mu_1^{\prime} = 16, \ \mu_2^{\prime} = 37, \ \mu_3^{\prime} = 25$ になります．

$\mu_0^{\prime}, \ \mu_1^{\prime}, \ \mu_2^{\prime}, \ \mu_3^{\prime}$ のそれぞれに対して，Upper関数を作用させることを考えると，

\begin{align*}
\displaystyle
\mathrm{Upper}_{p, q}(\mu_0^{\prime}) & = \frac{q}{p} \left \lfloor \frac{p \mu_0^{\prime}}{q} \right \rceil = 2^2 \left \lfloor \frac{1}{2^2} 53  \right \rceil = 2^2 \cdot 13 \\
\mathrm{Upper}_{p, q}(\mu_1^{\prime}) & = \frac{q}{p} \left \lfloor \frac{p \mu_1^{\prime}}{q} \right \rceil = 2^2 \left \lfloor \frac{1}{2^2} 16 \right \rceil = 2^2 \cdot 4 \\
\mathrm{Upper}_{p, q}(\mu_2^{\prime}) & = \frac{q}{p} \left \lfloor \frac{p \mu_2^{\prime}}{q} \right \rceil = 2^2 \left \lfloor \frac{1}{2} 37 \right  \rceil = 2^2 \cdot 9 \\
\mathrm{Upper}_{p, q}(\mu_3^{\prime}) & = \frac{q}{p} \left \lfloor \frac{p \mu_3^{\prime}}{q} \right \rceil = 2^2 \left \lfloor \frac{1}{2} 25 \right \rceil = 2^2 \cdot 6
\end{align*}

となります．

これでちゃんと plaintext の各係数に対して $\mathrm{Decode(Encode(} m \mathrm{))} = m$ が成り立っていることが確認できました．

以上で3.1の議論は終わりです．

今回の内容はここまでです．ここまでご覧になってくださった方々ありがとうございます！

「プログラマブルブートストラップの原著論文を理解する回」を理解する回 2/4