序
本記事はTRIAL&RetailAI Advent Calendar 202517日目の記事です。
昨日の記事は @tech_tuna さんのマグネットポンプをつかって自動灌水機をつくりたかったです。
家庭菜園の水やりを自動化したい!ということで試行錯誤されていました。(個人的には水耕栽培の部分が気になります)
本日は「1.26次元の図形?! ~フラクタル図形の次元を計算してみる~」。学生時代の研究テーマであったフラクタル図形のことを久しぶりに思い出して書いていました。
計算過程を図で見えるようにしていますので、数学が苦手な方も雰囲気を楽しんでいただければ幸いです。
なお、実装はD言語で行なっています。D言語については、昨年のアドベントカレンダーの記事でインストール方法や基本的な文法を紹介しております。興味のある方はぜひご覧ください。
フラクタル図形とは
フラクタル図形とは、「ものすごく複雑な図形」のことを言います。
以下はコッホ曲線と呼ばれる代表的なフラクタル図形です。ものすごく細かい折れ線から成る図形であることがわかります。
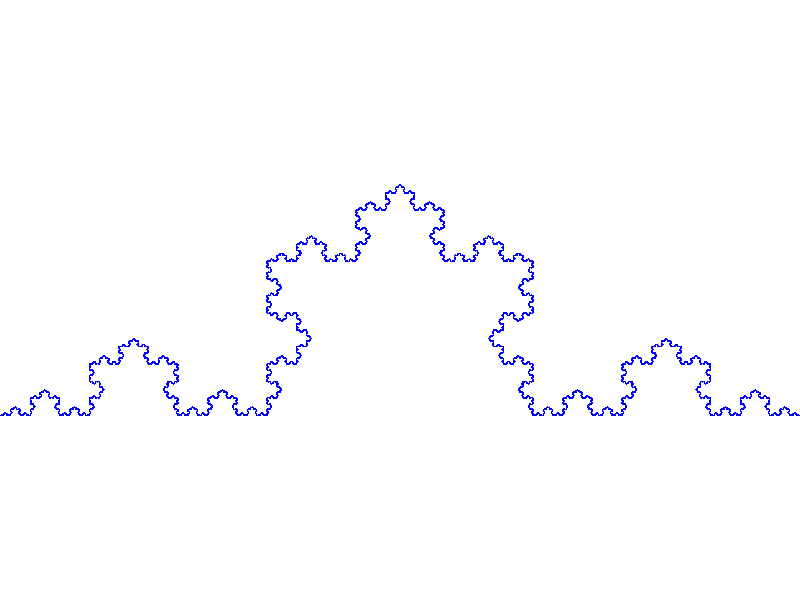
フラクタル図形は自然界にも存在しており、ロマネスコ1や海岸線などが例として知られています。
図形の複雑さについて、コッホ曲線を見てみましょう。
コッホ曲線は「自己相似図形」と言われる図形の1つです。
自己相似図形とは、自分自身を縮小したようなパーツで構成される図形のことを言います。コッホ曲線の場合だと、全体を1/3に縮小した4つのパーツから構成されています。
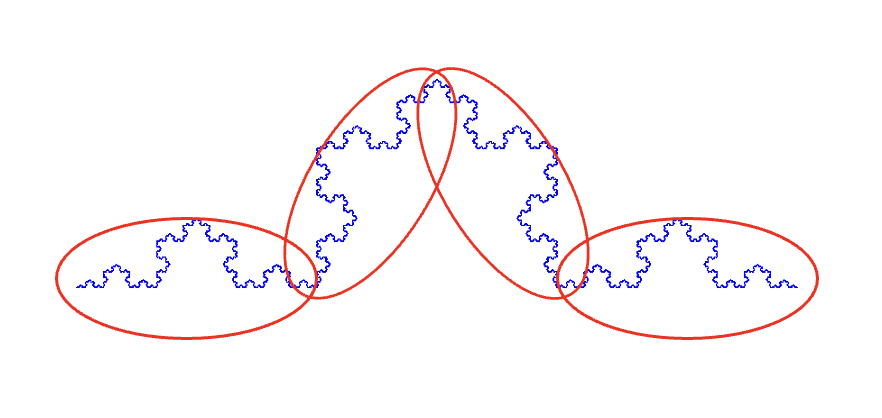
何気ない性質のようですが、コッホ曲線の長さを考えてみると2おかしなことに気づきます。
例えば、全体を3倍に拡大すると、図の丸で囲まれたパーツはそれぞれ元のコッホ曲線と同じものになります。よって、全体の長さは拡大前の4倍となります。
図形を3倍に拡大すると長さは元の3倍になるのが普通ですので、フラクタル図形の複雑さの一面を表していると言えます。このような複雑を表す指標に「フラクタル次元」というものがあります。
フラクタル次元
一口にフラクタル次元と言ってもさまざまな定義があるのですが、今回は ボックス次元 と呼ばれるものを扱います。
定義
フラクタル図形 $F$ について、1辺が $\varepsilon$ の格子と交わる個数を $N(\varepsilon)$ とする。
このとき、以下の極限$D$を$F$のボックス次元と呼ぶ。
D = \lim_{\varepsilon \rightarrow 0} \frac{N(\varepsilon)}{-\log \varepsilon}
ボックス次元には複数の定義があるのですがが3、その中でもコンピュータでの計算がしやすいものを紹介しました。今回は、この定義に基づいて計算してみようと思います。
いざ実装!
方針
以下の3つのモジュールに分けて実装します。
- フラクタル図形の点群を生成する
- フラクタル図形本体を描画する
- ボックス次元を計算する
- $-\log \varepsilon$と$\log N(\varepsilon)$の対応を作って、最小二乗法を使って傾きを計算する
- ついでに、ボックス次元を計算した各$\varepsilon$のステップをビジュアル化する
それぞれのモジュールは共通のインターフェースを使ってフラクタル図形の情報を受け渡しするようにします。
以下、具体的な実装を紹介していきますが、手っ取り早く結果が知りたい方は実行結果の部分まで飛ばしてください。
共通インターフェース
最初に座標の配列を渡すようなインターフェースを作っておきます。
後々いろんな図形を受け渡せるようにしたいので、シンプルな作りにしました。
struct Point
{
double x;
double y;
}
interface Fractal
{
Point[] generate();
}
フラクタル図形の点群の生成
各図形の点群を生成するようなコードを書いていきます。
ここでは、先ほど紹介したコッホ曲線を表す点群を生成します。
コッホ曲線は① → ②、② → ③のように直線部分を折れ線を置き換えていく処理を無限に続けると作ることができます。
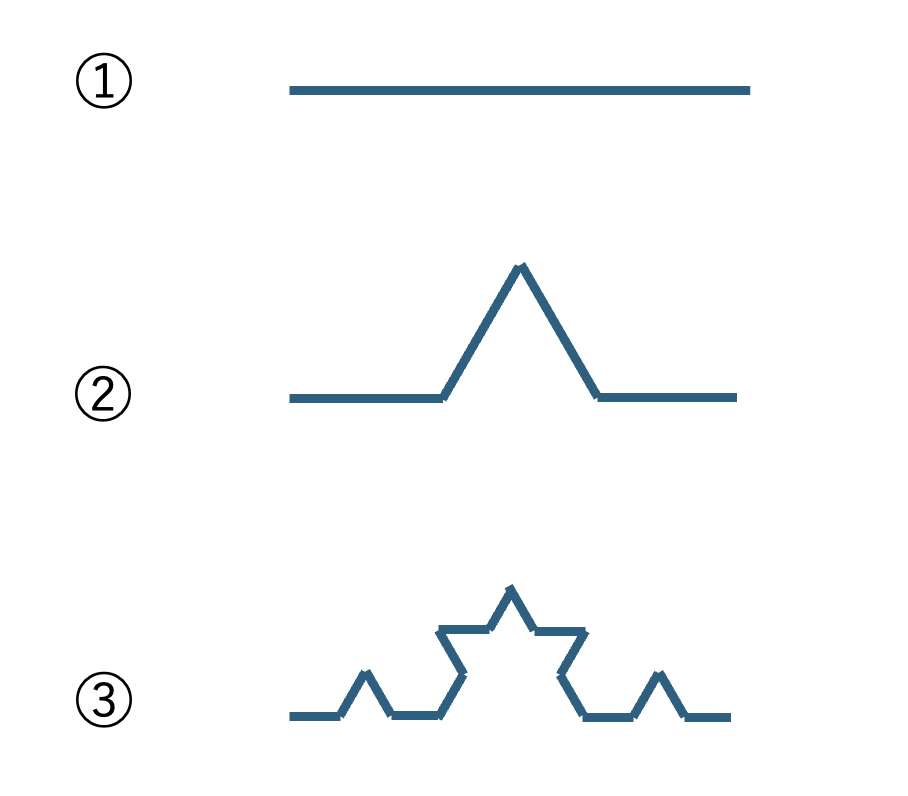
コードにすると以下のような再帰的な処理になります
void addKochVertices(ref Appender!(Point[]) app, Point p1, Point p5, int n) {
// 略。両橋の端点から折れ線の頂点を求める
// 4つの新しい線分に対して再帰呼び出し
addKochVertices(app, p1, p2, n - 1);
addKochVertices(app, p2, p3, n - 1);
addKochVertices(app, p3, p4, n - 1);
addKochVertices(app, p4, p5, n - 1);
}
コード全文(koch.d)
module generators.koch;
import fractal;
import std.math : PI, cos, sin;
import std.array : appender, Appender;
/**
* コッホ曲線を生成するクラス。
*/
class Koch : Fractal
{
private:
int _detail;
Point[] _points;
public:
/**
* コンストラクタ
* params:
* detail: コッホ曲線の再帰の深さ。0以上の値を指定します。
*/
this(int detail)
{
this._detail = detail;
}
/**
* コッホ曲線を構成する点群を生成します。
*
* 初回呼び出し時に点群を計算し、結果をキャッシュします。
* 2回目以降の呼び出しではキャッシュした値を返します。
*
* Returns:
* コッホ曲線の頂点配列。
*/
override Point[] generate()
{
if (_points.length > 0)
{
return _points;
}
auto pointAppender = appender!(Point[])();
// 初期線分を (0,0) -> (1,0) とする
auto p1 = Point(0.0, 0.0);
auto p5 = Point(1.0, 0.0);
pointAppender.put(p1);
addKochVertices(pointAppender, p1, p5, _detail);
_points = pointAppender.data;
return _points;
}
private:
/**
* 2点間にコッホ曲線の頂点を再帰的に追加する。
*
* params:
* app: 結果を格納するAppender
* p1: 始点
* p5: 終点
* n: 残りの再帰回数
*/
void addKochVertices(ref Appender!(Point[]) app, Point p1, Point p5, int n)
{
if (n == 0)
{
app.put(p5);
return;
}
// 線分を3等分するベクトル
auto v = Point((p5.x - p1.x) / 3.0, (p5.y - p1.y) / 3.0);
// 3等分点
auto p2 = Point(p1.x + v.x, p1.y + v.y);
auto p4 = Point(p1.x + 2 * v.x, p1.y + 2 * v.y);
// p2->p4 のベクトルを60度回転させて、三角形の頂点p3を求める
// 回転行列:
// | cos(a) -sin(a) |
// | sin(a) cos(a) |
const double angle = 60.0 * PI / 180.0; // ラジアンに変換
auto rotated_v = Point(
v.x * cos(angle) - v.y * sin(angle),
v.x * sin(angle) + v.y * cos(angle)
);
auto p3 = Point(p2.x + rotated_v.x, p2.y + rotated_v.y);
// 4つの新しい線分に対して再帰呼び出し
addKochVertices(app, p1, p2, n - 1);
addKochVertices(app, p2, p3, n - 1);
addKochVertices(app, p3, p4, n - 1);
addKochVertices(app, p4, p5, n - 1);
}
}
図形の描画
pngファイルを出力します。
今回の本題ではないので、コードを載せるに留めます。
コード全文(drawing.d)
module drawing;
import fractal;
import std.stdio;
import std.math : isNaN;
import std.math.traits : isInfinity;
import std.algorithm : min, max;
import imageformats;
/**
* RGBカラーを表現する構造体。
*/
struct Color
{
ubyte r, g, b;
}
// 使いやすいように、いくつかの色を定数として定義
immutable Color COLOR_BLACK = Color(0, 0, 0);
immutable Color COLOR_WHITE = Color(255, 255, 255);
immutable Color COLOR_RED = Color(255, 0, 0);
immutable Color COLOR_GREEN = Color(0, 255, 0);
immutable Color COLOR_BLUE = Color(0, 0, 255);
/**
* 点群データを画像ファイルとして描画します。
*
* params:
* points: 描画する点の配列。
* filePath: 出力する画像ファイルのパス。拡張子によって形式が決まります (e.g., .png, .jpg)。
* width: 画像の幅(ピクセル単位)。
* height: 画像の高さ(ピクセル単位)。
* foreground: 点の色。
* background: 背景色。
*/
void drawPoints(
const Point[] points,
string filePath,
int width,
int height,
Color foreground = COLOR_WHITE,
Color background = COLOR_BLACK)
in (width > 0 && height > 0, "Image width and height must be positive.")
{
// 1. キャンバスを作成し、背景色で塗りつぶす
auto canvas = new Color[width * height];
foreach (i; 0 .. canvas.length)
{
canvas[i] = background;
}
// 点がなければ、背景のみの画像を書き出して終了
if (points.length == 0)
{
writeImage(filePath, width, height, canvas);
return;
}
// 2. 点群のバウンディングボックス(描画範囲)を計算
double minX = points[0].x, maxX = points[0].x;
double minY = points[0].y, maxY = points[0].y;
foreach (ref p; points[1 .. $])
{
if (p.x.isNaN || isInfinity(p.x) || p.y.isNaN || isInfinity(p.y)) continue;
minX = min(minX, p.x);
maxX = max(maxX, p.x);
minY = min(minY, p.y);
maxY = max(maxY, p.y);
}
// 3. アスペクト比を維持したまま、画像に収まるようにスケーリング係数を計算
double boxWidth = maxX - minX;
double boxHeight = maxY - minY;
// 点が1点だけ、あるいは直線上に並んでいる場合のゼロ除算を防止
if (boxWidth < 1e-9) boxWidth = 1.0;
if (boxHeight < 1e-9) boxHeight = 1.0;
auto scaleX = (width - 1.0) / boxWidth;
auto scaleY = (height - 1.0) / boxHeight;
auto scale = min(scaleX, scaleY);
// 4. 画像を中央に配置するためのオフセットを計算
double offsetX = (width - boxWidth * scale) / 2.0;
double offsetY = (height - boxHeight * scale) / 2.0;
// 5. すべての点をキャンバス上のピクセルにマッピング
foreach (ref p; points)
{
if (p.x.isNaN || isInfinity(p.x) || p.y.isNaN || isInfinity(p.y)) continue;
// フラクタル座標をピクセル座標に変換
int px = cast(int)((p.x - minX) * scale + offsetX);
// 画像のY座標は下が正だが、数学座標は上が正なので反転させる
int py = cast(int)((maxY - p.y) * scale + offsetY);
// 座標がキャンバスの範囲内にあることを確認
if (px >= 0 && px < width && py >= 0 && py < height)
{
canvas[py * width + px] = foreground;
}
}
// 6. キャンバスデータを画像ファイルに書き出す
writeImage(filePath, width, height, canvas);
}
/**
* 画像ファイルを書き出すヘルパー関数。
* imageformatsライブラリを利用し、ファイル名の拡張子からフォーマットを自動判別する。
*/
void writeImage(string filePath, int width, int height, const Color[] canvas)
{
// constな配列を書き換え可能なスライスに変換
auto data = cast(ubyte[])(cast(void*)canvas.ptr)[0 .. canvas.length * 3];
// imageformats.write_image 関数を正しい引数の順序で呼び出す
imageformats.write_image(filePath, width, height, data);
}
ボックス次元の計算
格子の数を小さくしていって、コッホ曲線と交わる格子の数を数え上げていきます。
計算途中のイメージはこんな感じです。
ピクセルで直線を近似する「ブレゼンハムのアルゴリズム」というものがあので、これをコッホ曲線を構成する各直線に使います。
この近似で使われたピクセルの総数が、コッホ曲線と交わる格子の数となるわけです。
// (x0, y0) と (x1, y1)を結ぶ直線を一辺 width のピクセルで近似し、結果をcanvasに格納する
// canvasは2次元配列を1次元配列に折りたたんだ形で表現している
private void drawLine(bool[] canvas, int width, int x0, int y0, int x1, int y1)
{
int dx = abs(x1 - x0);
int sx = x0 < x1 ? 1 : -1;
int dy = -abs(y1 - y0);
int sy = y0 < y1 ? 1 : -1;
int err = dx + dy;
while (true)
{
// 今いるマスを `true`に書き換えて
if (x0 >= 0 && x0 < width && y0 >= 0 && y0 < width)
{
canvas[y0 * width + x0] = true;
}
if (x0 == x1 && y0 == y1) break;
int e2 = 2 * err;
// 次にx方向、y方向どちらのマスへ進むか判断する
if (e2 >= dy) { err += dy; x0 += sx; }
if (e2 <= dx) { err += dx; y0 += sy; }
}
}
このようにして交差するマスの数を一通り計算したら最小二乗法で計算します。
一次式の場合、$\Sigma x_k$, $\Sigma y_k$, $\Sigma x_k y_k$, $\Sigma x_k^2$ の値を使って傾きと切片が求まります。
private Line leastSquaresLine(const Point[] data)
{
if (data.length < 2) return Line(0.0, 0.0);
double sumX = 0.0, sumY = 0.0, sumXY = 0.0, sumX2 = 0.0;
foreach (p; data)
{
sumX += p.x;
sumY += p.y;
sumXY += p.x * p.y;
sumX2 += p.x * p.x;
}
immutable double n = data.length;
immutable double denominator = n * sumX2 - sumX * sumX;
if (abs(denominator) < 1e-9) return Line(0.0, 0.0);
double slope = (n * sumXY - sumX * sumY) / denominator;
double intercept = (sumY - slope * sumX) / n;
// slope(傾き)の値が今回欲しい値
return Line(slope, intercept);
}
コード全文(boxcounting.d)
module boxcounting;
import fractal;
import std.math : log, abs, round;
import std.algorithm : min, max, each, map;
import std.array : array;
/**
* 直線 (y = slope * x + intercept) を表現する構造体。
*/
struct Line
{
double slope;
double intercept;
}
/**
* ボックスカウント次元の計算結果を格納する構造体。
*/
struct BoxCountResult
{
double dimension; /// 計算されたフラクタル次元
Point[] logLogData; /// log(1/ε) vs log(N(ε)) のプロット用データ
Point[] rawCounts; /// (ボックスサイズ ε, 交差するボックス数 N(ε)) の生データ
Line regressionLine; /// ログプロットの回帰直線
}
// --- プライベートヘルパー関数 ---
/**
* 最小二乗法を用いて、点群に最もフィットする直線を計算する。
*/
private Line leastSquaresLine(const Point[] data)
{
if (data.length < 2) return Line(0.0, 0.0);
double sumX = 0.0, sumY = 0.0, sumXY = 0.0, sumX2 = 0.0;
foreach (p; data)
{
sumX += p.x;
sumY += p.y;
sumXY += p.x * p.y;
sumX2 += p.x * p.x;
}
immutable double n = data.length;
immutable double denominator = n * sumX2 - sumX * sumX;
if (abs(denominator) < 1e-9) return Line(0.0, 0.0);
double slope = (n * sumXY - sumX * sumY) / denominator;
double intercept = (sumY - slope * sumX) / n;
return Line(slope, intercept);
}
/**
* ブレゼンハムのアルゴリズムを用いて、キャンバス上に線を描画する。
*/
private void drawLine(
bool[] canvas,
int width,
int x0, int y0,
int x1, int y1)
{
int dx = abs(x1 - x0);
int sx = x0 < x1 ? 1 : -1;
int dy = -abs(y1 - y0);
int sy = y0 < y1 ? 1 : -1;
int err = dx + dy;
while (true)
{
if (x0 >= 0 && x0 < width && y0 >= 0 && y0 < width)
{
canvas[y0 * width + x0] = true;
}
if (x0 == x1 && y0 == y1) break;
int e2 = 2 * err;
if (e2 >= dy) { err += dy; x0 += sx; }
if (e2 <= dx) { err += dx; y0 += sy; }
}
}
// --- 公開API ---
/**
* ラスタライズ法を用いて、ポリライン(折れ線)として解釈した点群のボックスカウント次元を計算する。
*
* params:
* points: フラクタルを構成する点の配列。配列の順序通りに線で結ばれると仮定する。
* connectPoints: 点を線で結んでラスタライズするかどうか。
* canvasSize: ラスタライズに用いる内部キャンバスの解像度。高いほど精度が上がるが、メモリを消費する。
* minBoxSize: テストする最小のボックスサイズ。
* maxBoxSize: テストする最大のボックスサイズ。
* returns:
* 次元とログプロットデータを含む BoxCountResult。
*/
BoxCountResult calculateDimension(
const Point[] points,
bool connectPoints,
int canvasSize = 4096,
int minBoxSize = 2,
int maxBoxSize = 1024)
{
if (points.length == 0)
{
return BoxCountResult(0.0, null, null, Line(0,0));
}
// 1. 仮想キャンバスを作成
auto canvas = new bool[canvasSize * canvasSize]; // デフォルトでfalseに初期化
// 2. 点群のバウンディングボックスを計算し、スケーリング係数を決定
double minX = points[0].x, maxX = points[0].x;
double minY = points[0].y, maxY = points[0].y;
foreach (ref p; points[1 .. $])
{
minX = min(minX, p.x);
maxX = max(maxX, p.x);
minY = min(minY, p.y);
maxY = max(maxY, p.y);
}
double boxWidth = maxX - minX;
double boxHeight = maxY - minY;
if (boxWidth < 1e-9) boxWidth = 1.0;
if (boxHeight < 1e-9) boxHeight = 1.0;
double scale = min((canvasSize - 1.0) / boxWidth, (canvasSize - 1.0) / boxHeight);
double offsetX = (canvasSize - boxWidth * scale) / 2.0;
double offsetY = (canvasSize - boxHeight * scale) / 2.0;
// 3. キャンバスにフラクタルを描画(ラスタライズ)
if (connectPoints && points.length >= 2)
{
// 点を線で結ぶ場合 (ポリライン)
for (size_t i = 0; i < points.length - 1; ++i)
{
auto p1 = points[i];
auto p2 = points[i+1];
int x0 = cast(int)round((p1.x - minX) * scale + offsetX);
int y0 = cast(int)round((maxY - p1.y) * scale + offsetY);
int x1 = cast(int)round((p2.x - minX) * scale + offsetX);
int y1 = cast(int)round((maxY - p2.y) * scale + offsetY);
drawLine(canvas, canvasSize, x0, y0, x1, y1);
}
}
else
{
// 点のみを描画する場合 (ポイントクラウド)
foreach(ref p; points)
{
int px = cast(int)round((p.x - minX) * scale + offsetX);
int py = cast(int)round((maxY - p.y) * scale + offsetY);
if (px >= 0 && px < canvasSize && py >= 0 && py < canvasSize)
{
canvas[py * canvasSize + px] = true;
}
}
}
// 4. 様々なボックスサイズで、図形を覆うボックス数を数える
Point[] counts;
for (int boxSize = minBoxSize; boxSize <= maxBoxSize; boxSize *= 2)
{
long numBoxes = 0;
for (int y = 0; y < canvasSize; y += boxSize)
{
for (int x = 0; x < canvasSize; x += boxSize)
{
bool found = false;
for (int j = 0; j < boxSize && y + j < canvasSize; ++j)
{
for (int k = 0; k < boxSize && x + k < canvasSize; ++k)
{
if (canvas[(y + j) * canvasSize + (x + k)])
{
numBoxes++;
found = true;
break;
}
}
if (found) break;
}
}
}
if (numBoxes > 0)
{
counts ~= Point(cast(double)boxSize, cast(double)numBoxes);
}
}
// 5. ログプロットデータを作成し、最小二乗法で傾き(次元)を計算
if (counts.length < 2)
{
return BoxCountResult(0.0, null, null, Line(0,0));
}
auto logLogData = counts.map!(p => Point(log(1.0/p.x), log(p.y))).array;
auto line = leastSquaresLine(logLogData);
return BoxCountResult(line.slope, logLogData, counts, line);
}
また、ボックス次元の計算過程を可視化するコード、両対数グラフを描画するコードも合わせて実装しました。この2つについては、以下のコード全文の通りです。
コード全文(visualization.d)
module visualization;
import fractal;
import drawing; // Color構造体と画像書き出し関数を再利用
import std.stdio;
import std.math : abs, round;
import std.algorithm : min, max;
import core.stdc.string : memset;
// --- プライベートヘルパー関数 ---
/**
* 2つの色をアルファブレンディングで合成する。
* result = foreground * alpha + background * (1 - alpha)
*/
private Color blend(Color foreground, Color background, double alpha)
{
return Color(
cast(ubyte)(foreground.r * alpha + background.r * (1 - alpha)),
cast(ubyte)(foreground.g * alpha + background.g * (1 - alpha)),
cast(ubyte)(foreground.b * alpha + background.b * (1 - alpha))
);
}
/**
* ブレゼンハムのアルゴリズム(visualization.d内のプライベート版)
*/
private void drawLine(bool[] canvas, int width, int x0, int y0, int x1, int y1)
{
int dx = abs(x1 - x0);
int sx = x0 < x1 ? 1 : -1;
int dy = -abs(y1 - y0);
int sy = y0 < y1 ? 1 : -1;
int err = dx + dy;
while (true)
{
if (x0 >= 0 && x0 < width && y0 >= 0 && y0 < width)
{
canvas[y0 * width + x0] = true;
}
if (x0 == x1 && y0 == y1) break;
int e2 = 2 * err;
if (e2 >= dy) { err += dy; x0 += sx; }
if (e2 <= dx) { err += dx; y0 += sy; }
}
}
// --- 公開API ---
/**
* ボックスカウントの過程を画像として可視化する。
*
* params:
* points: フラクタルを構成する点の配列。
* filePath: 出力する画像ファイルのパス (e.g., .png)。
* width: 画像の幅。
* height: 画像の高さ。
* boxSize: 可視化するボックス(格子)のサイズ。
*/
void visualizeBoxCounting(
const Point[] points,
bool connectPoints,
string filePath,
int width,
int height,
int boxSize)
{
// 1. キャンバスを作成し、背景色で塗りつぶす
auto canvas = new Color[width * height];
foreach (i; 0 .. canvas.length) { canvas[i] = COLOR_BLACK; }
if (points.length == 0)
{
writeImage(filePath, width, height, canvas);
return;
}
// 2. スケーリング係数を計算 (drawing.d と同じロジック)
double minX = points[0].x, maxX = points[0].x;
double minY = points[0].y, maxY = points[0].y;
foreach (ref p; points[1 .. $])
{
minX = min(minX, p.x); maxX = max(maxX, p.x);
minY = min(minY, p.y); maxY = max(maxY, p.y);
}
double boxWidth = maxX - minX;
double boxHeight = maxY - minY;
if (boxWidth < 1e-9) boxWidth = 1.0;
if (boxHeight < 1e-9) boxHeight = 1.0;
double scale = min((width - 1.0) / boxWidth, (height - 1.0) / boxHeight);
double offsetX = (width - boxWidth * scale) / 2.0;
double offsetY = (height - boxHeight * scale) / 2.0;
// 3. フラクタル図形をキャンバスに描画 (白)
// (可視化のため、ここでは常に点のみを描画)
foreach (ref p; points)
{
int px = cast(int)round((p.x - minX) * scale + offsetX);
int py = cast(int)round((maxY - p.y) * scale + offsetY);
if (px >= 0 && px < width && py >= 0 && py < height)
{
canvas[py * width + px] = COLOR_WHITE;
}
}
// 4. 図形と交差するボックスを特定
auto intersectingBoxes = new bool[(width / boxSize + 1) * (height / boxSize + 1)];
if (connectPoints && points.length >= 2)
{
// 線で結ぶ場合
for (size_t i = 0; i < points.length - 1; ++i)
{
auto p1 = points[i];
auto p2 = points[i+1];
int x0 = cast(int)round((p1.x - minX) * scale + offsetX);
int y0 = cast(int)round((maxY - p1.y) * scale + offsetY);
int x1 = cast(int)round((p2.x - minX) * scale + offsetX);
int y1 = cast(int)round((maxY - p2.y) * scale + offsetY);
// 線分上の各ピクセルがどのボックスに属するかを記録
int dx = abs(x1 - x0), sx = x0 < x1 ? 1 : -1;
int dy = -abs(y1 - y0), sy = y0 < y1 ? 1 : -1;
int err = dx + dy;
while(true)
{
if (x0 >= 0 && x0 < width && y0 >= 0 && y0 < height)
{
int gridX = x0 / boxSize;
int gridY = y0 / boxSize;
intersectingBoxes[gridY * (width / boxSize + 1) + gridX] = true;
}
if (x0 == x1 && y0 == y1) break;
int e2 = 2 * err;
if (e2 >= dy) { err += dy; x0 += sx; }
if (e2 <= dx) { err += dx; y0 += sy; }
}
}
}
else
{
// 点のみの場合
foreach(ref p; points)
{
int px = cast(int)round((p.x - minX) * scale + offsetX);
int py = cast(int)round((maxY - p.y) * scale + offsetY);
if (px >= 0 && px < width && py >= 0 && py < height)
{
int gridX = px / boxSize;
int gridY = py / boxSize;
intersectingBoxes[gridY * (width / boxSize + 1) + gridX] = true;
}
}
}
// 5. 交差するボックスを半透明の赤色でハイライト
auto highlightColor = COLOR_RED;
for (int gridY = 0; gridY < height / boxSize + 1; ++gridY)
{
for (int gridX = 0; gridX < width / boxSize + 1; ++gridX)
{
if (intersectingBoxes[gridY * (width / boxSize + 1) + gridX])
{
int startX = gridX * boxSize;
int startY = gridY * boxSize;
for (int y = startY; y < startY + boxSize && y < height; ++y)
{
for (int x = startX; x < startX + boxSize && x < width; ++x)
{
canvas[y * width + x] = blend(highlightColor, canvas[y * width + x], 0.4);
}
}
}
}
}
// 6. グリッド線を描画 (青)
auto gridColor = COLOR_BLUE;
for (int y = 0; y < height; ++y)
{
for (int x = 0; x < width; ++x)
{
if (x % boxSize == 0 || y % boxSize == 0)
{
canvas[y * width + x] = blend(gridColor, canvas[y * width + x], 0.6);
}
}
}
// 7. 画像ファイルに書き出し
writeImage(filePath, width, height, canvas);
}
コード全文(plotting.d)
module plotting;
import fractal;
import boxcounting; // For Line struct
import std.stdio;
import std.format;
import std.math : floor, ceil;
import std.algorithm : min, max;
/**
* 両対数プロットをSVGファイルとして書き出す。
*
* params:
* data: log-logデータ点の配列
* regressionLine: データにフィットさせた回帰直線
* filePath: 出力するSVGファイルのパス
*/
void writeLogLogPlotSVG(
const Point[] data,
Line regressionLine,
string filePath)
{
if (data.length == 0) return;
// --- SVGとグラフの基本設定 ---
immutable int width = 600;
immutable int height = 500;
immutable int margin = 60;
immutable int plotWidth = width - margin * 2;
immutable int plotHeight = height - margin;
// --- データ範囲の計算 ---
double raw_minX = data[0].x, raw_maxX = data[0].x;
double raw_minY = data[0].y, raw_maxY = data[0].y;
foreach (p; data)
{
raw_minX = min(raw_minX, p.x);
raw_maxX = max(raw_maxX, p.x);
raw_minY = min(raw_minY, p.y);
raw_maxY = max(raw_maxY, p.y);
}
// 2. 縦横の軸の幅が同じになり、かつキリの良い数値になるように調整
double xRange = raw_maxX - raw_minX;
if (xRange < 1e-9) xRange = 1.0; // ゼロ除算防止
double yRange = raw_maxY - raw_minY;
if (yRange < 1e-9) yRange = 1.0; // ゼロ除算防止
double maxDataRange = max(xRange, yRange);
// 軸の最終的な表示範囲を決定 (5区間に分割するため、5の倍数になるように調整)
// データ範囲に少しマージンを加え、5で割り切れるように切り上げる
double finalRange = ceil((maxDataRange + 2.0) / 5.0) * 5.0; // +2.0は両端に1ずつのマージン
double xCenter = (raw_maxX + raw_minX) / 2.0;
double yCenter = (raw_maxY + raw_minY) / 2.0;
double minX = floor(xCenter - finalRange / 2.0);
double maxX = minX + finalRange;
double minY = floor(yCenter - finalRange / 2.0);
double maxY = minY + finalRange;
// --- SVGファイルを開く ---
auto file = File(filePath, "w");
file.writeln(`<?xml version="1.0" standalone="no"?>`);
file.writeln(`<svg width="`, width, `" height="`, height, `" xmlns="http://www.w3.org/2000/svg">`);
// --- 背景 ---
file.writeln(` <rect width="100%" height="100%" fill="white"/>`);
// --- 軸とグリッド線 ---
file.writeln(` <g class="grid" stroke="#ccc" stroke-dasharray="2,2">`);
// X軸グリッド (5本)
foreach(i; 0 .. 6)
{
double x = margin + i * plotWidth / 5.0;
file.writeln(` <line x1="`, x, `" y1="`, margin, `" x2="`, x, `" y2="`, plotHeight, `"/>`);
}
// Y軸グリッド (5本)
foreach(i; 0 .. 6)
{
double y = margin + i * (plotHeight - margin) / 5.0;
file.writeln(` <line x1="`, margin, `" y1="`, y, `" x2="`, margin + plotWidth, `" y2="`, y, `"/>`);
}
file.writeln(` </g>`);
// --- 軸ラベル ---
file.writeln(` <g class="labels" font-family="sans-serif" font-size="12">`);
// X軸ラベル
file.writeln(` <text x="`, width / 2, `" y="`, height - 10, `" text-anchor="middle">log(1/ε)</text>`);
// Y軸ラベル
file.writeln(` <text transform="translate(15, `, height / 2, `) rotate(-90)" text-anchor="middle">log(N(ε))</text>`);
// X軸の数値
foreach(i; 0 .. 6)
{
double val = minX + i * (maxX - minX) / 5.0;
double x = margin + i * plotWidth / 5.0;
file.writeln(` <text x="`, x, `" y="`, plotHeight + 20, `" text-anchor="middle">`, format("%.1f", val), `</text>`);
}
// Y軸の数値
foreach(i; 0 .. 6)
{
double val = maxY - i * (maxY - minY) / 5.0;
double y = margin + i * (plotHeight - margin) / 5.0;
file.writeln(` <text x="`, margin - 10, `" y="`, y + 4, `" text-anchor="end">`, format("%.1f", val), `</text>`);
}
file.writeln(` </g>`);
// --- データ点 ---
file.writeln(` <g class="data-points" fill="#f44336">`);
foreach (p; data)
{
double cx = margin + (p.x - minX) / (maxX - minX) * plotWidth;
double cy = margin + (maxY - p.y) / (maxY - minY) * (plotHeight - margin);
file.writeln(` <circle cx="`, cx, `" cy="`, cy, `" r="3"/>`);
}
file.writeln(` </g>`);
// --- 回帰直線 ---
double y1 = regressionLine.slope * minX + regressionLine.intercept;
double y2 = regressionLine.slope * maxX + regressionLine.intercept;
double x1_svg = margin;
double y1_svg = margin + (maxY - y1) / (maxY - minY) * (plotHeight - margin);
double x2_svg = margin + plotWidth;
double y2_svg = margin + (maxY - y2) / (maxY - minY) * (plotHeight - margin);
file.writeln(` <line x1="`, x1_svg, `" y1="`, y1_svg, `" x2="`, x2_svg, `" y2="`, y2_svg, `" stroke="#2196f3" stroke-width="2"/>`);
file.writeln(`</svg>`);
}
main関数
あとは順に呼び出していくだけです
module app;
import std.stdio;
import std.math : log;
import std.getopt;
import std.format : format;
import std.string : toLower;
import fractal;
import boxcounting;
import visualization;
import drawing;
import plotting;
// ジェネレータのインポート
import generators.koch;
void main(string[] args)
{
// --- 1. コマンドライン引数の設定と解析 ---
string fractalType = "koch";
int detail = 7;
int width = 800;
int height = 600;
// 一応
getopt(args,
"fractal", "Fractal type (koch, sierpinski, line, mandelbrot)", &fractalType,
"detail", "Recursion detail for Koch curve", &detail,
);
fractalType = fractalType.toLower();
writeln("--- Fractal Dimension Tool ---");
// --- 2. ジェネレータの選択とインスタンス化 ---
Fractal generator;
string fractalName;
bool connectPoints;
switch (fractalType)
{
case "koch":
fractalName = "Koch Curve";
generator = new Koch(detail);
connectPoints = true;
writeln("Generator: ", fractalName, " (detail: ", detail, ")");
break;
default:
stderr.writeln("Error: Unknown fractal type '", fractalType, "'");
stderr.writeln("Available types are: koch, sierpinski, line, mandelbrot");
return;
}
// --- 3. フラクタルデータの生成 ---
writeln("Generating points...");
Point[] points = generator.generate();
writeln(points.length, " points generated.");
// --- 4. フラクタルの描画 ---
string outputFile = format("output/fractals/%s.ppm", fractalType);
writeln("Drawing image to ", outputFile, "...");
drawPoints(points, outputFile, width, height, COLOR_BLUE, COLOR_WHITE);
writeln("Image saved.");
// --- 5. フラクタル次元の計算 ---
writeln("Calculating box-counting dimension...");
auto result = calculateDimension(points, connectPoints);
// --- 6. 結果の表示 ---
writeln("----------------------------------------");
if (fractalType == "koch")
{
writeln("Theoretical dimension: ", log(4.0) / log(3.0));
}
writeln("Calculated dimension: ", result.dimension);
writeln("----------------------------------------");
writeln("Box-counting data (Box Size ε, Intersecting Boxes N(ε)):");
writeln(" ε N(ε)");
writeln("--------------------");
if (result.rawCounts !is null)
{
foreach (p; result.rawCounts)
{
writefln(" %-9.1f %-9.0f", p.x, p.y);
}
}
writeln("----------------------------------------");
// --- 7. グラフの生成 ---
if (result.logLogData !is null)
{
string plotOutputFile = format("output/plots/%s_loglog_plot.svg", fractalType);
writeln("Generating log-log plot to ", plotOutputFile, "...");
writeLogLogPlotSVG(result.logLogData, result.regressionLine, plotOutputFile);
}
// --- 8. ボックスカウント過程の可視化 ---
writeln("Generating visualization images...");
foreach (boxSize; [128, 64, 32, 16, 8, 4, 2])
{
string visOutputFile = format("output/visualization/%s_%s.ppm", fractalType, boxSize);
writeln(" - Generating ", visOutputFile, " (box size: ", boxSize, ")");
visualizeBoxCounting(points, connectPoints, visOutputFile, width, height, boxSize);
}
writeln("----------------------------------------");
writeln("Program finished successfully.");
}
実行!
今まで作ってきたファイルをこんな感じで並べて
.
├─ app.d
├─ boxcounting.d
├─ darwing.d
├─ fractal.d
├─ plotting.d
├─ visualization.d
└─ generators
│ └─ koch.d
└─ dub.json
dub.json には以下を記載します。dependenciesで指定しているものは画像生成で使うライブラリです。
{
"dependencies": {
"imageformats": "~>7.0.2"
},
"importPaths": [
"."
],
"name": "fractal-dimension",
"sourcePaths": [
"."
],
"targetType": "executable"
}
いざ実行!
dub run -- --fractal=koch --detail=7
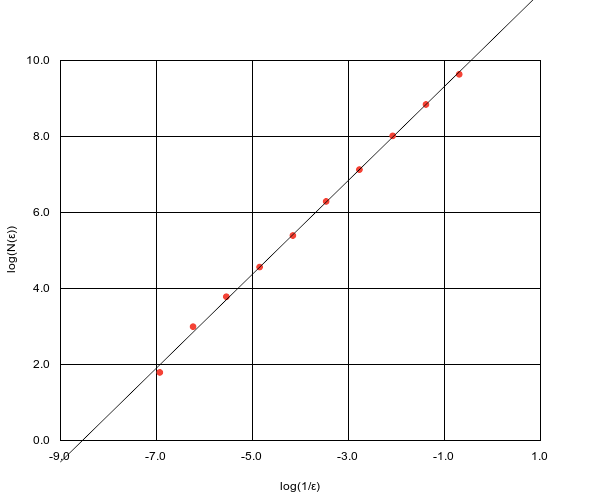
実行結果は以下のようになりました。
| $\varepsilon$ | 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 |
|---|---|---|---|---|---|---|---|---|---|---|
| $N(\varepsilon)$ | 6 | 20 | 44 | 96 | 220 | 540 | 1248 | 3033 | 6922 | 15310 |
$\varepsilon$を半分にしていくと、$N(\varepsilon)$の値が2.5~6倍程度に増えていくのがわかります。4
なお、$\varepsilon$の値は、生成した点群に対する仮想的なピクセル数のようなものであり、座標上の点とは異なります。そのため、2、4、8...のような整数の値になっています。
最小二乗法を用いて上のグラフの傾きを求めた結果は、1.23535となりました。
考察
コッホ曲線の正確なボックス次元の値は$\frac{\log4}{\log3} = 1.26186...$です。(タイトルにある1.26はこの値です)
先ほどの計算結果では1.23程度で実際の値より小さく出てしまいました。
理由としては、
- コッホ曲線をコンピュータで扱う際に、無限回の再帰を有限回止めている
という点が大きそうです。
改善方法としては
- 単純に再帰の回数を増やす(計算回数やメモリなどの計算リソースとの兼ね合いはあるが)
- コッホ曲線の「自己相似図形」という性質を活かした計算アルゴリズムにする(今回は図形の性質に依存しないようにボックス次元の計算部分を実装したので)
などがありそうです。
学生時代に読んだ本には、ただただ「コンピュータで計算が容易」とだけ書かれていたのですが、実装を行ってみると、工夫の余地がありそうで面白いと思いました。
結
ここまでお読みいただきありがとうございました。
明日は、 @ido_shun さんの「エンジニアって大変なんやで。」です。お楽しみに!
RetailAIとTRIALではエンジニアを募集しています。
興味がある方はご連絡ください!
https://recruit.jobcan.jp/retail-ai/
https://hrmos.co/pages/trialgp/jobs?category=2020003768196907008
-
やたらフラクタル図形の例として出される野菜。イマイチ調理方法がわからないが、どうやらカリフラワーの一種らしい。https://ja.wikipedia.org/wiki/%E3%83%AD%E3%83%9E%E3%83%8D%E3%82%B9%E3%82%B3 ↩
-
実際はコッホ曲線の長さは$\infty$であり、定義できないことに注意。 ↩
-
当然ながら、どの定義を使っても同じボックス次元の値が得られる。書籍などでは、図形の被覆に基づく定義が最初に出てくるのが一般的。 ↩
-
普通の曲線なら、$\varepsilon$を半分にしていくと、おおよそ2倍になる。 ↩