【PyTorch】Vision Transformer (ViT) を自作しながら解説する

はじめに

この記事では、2021年に Google Brain が発表した Vision Transformer (ViT) に関する論文「AN IMAGE IS WORTH 16X16 WORDS: TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE」を、筆者が自分で実装しながら解説していきます。完成したコードは以下で公開しています。

前提としていること

以下のことは、この記事では解説しません。

• 基本的な Python, PyTorch の使い方
• 基本的なニューラルネット系のモデルの仕組みについて

例えば、以下のコードが理解できるくらいの方を想定しています。

PyTorch による AlexNet の実装

import torch
import torch.nn as nn


class AlexNet(nn.Module):
    def __init__(self, num_classes=1000):
        super().__init__()
        self.features = nn.Sequential(
            nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
            nn.Conv2d(64, 192, kernel_size=5, padding=2),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
            nn.Conv2d(192, 384, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(384, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(256, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
        )
        self.avgpool = nn.AdaptiveAvgPool2d((6, 6))
        self.classifier = nn.Sequential(
            nn.Dropout(p=0.5),
            nn.Linear(256 * 6 * 6, 4096),
            nn.ReLU(inplace=True),
            nn.Dropout(p=0.5),
            nn.Linear(4096, 4096),
            nn.ReLU(inplace=True),
            nn.Linear(4096, num_classes),
        )

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        x = self.features(x)
        x = self.avgpool(x)
        x = torch.flatten(x, 1)
        x = self.classifier(x)
        return x

この記事のゴール

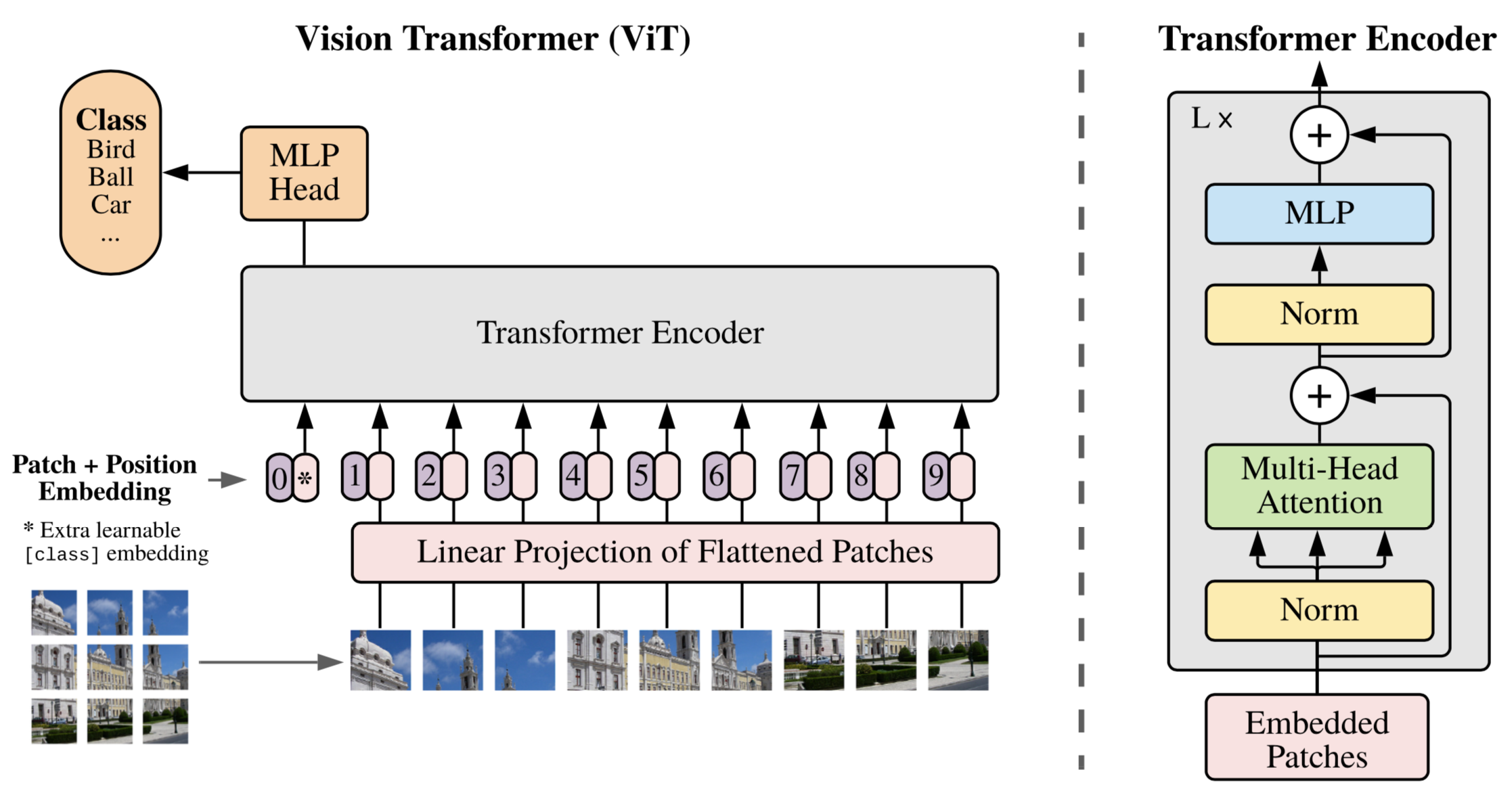
この記事で実装・解説していくモデルの全体像は以下の図です。この記事のゴールは、このモデルについて理解し、PyTorch を用いて実装することです。

この記事の大まかな流れ

以下のような流れで説明していきます。

• Transformer とは
• ViT とは
• ViT を作る
• ViT を使ってみる

Transformer とは

「Vision Transformer (ViT)」 = 「Transformer を画像認識に応用したもの」なので、ViT について説明する前に Transformer について簡単に説明します。

Transformer とは、2017年に「Attention Is All You Need」という論文の中で発表された深層学習モデルです。「英語→フランス語」のような自然言語の翻訳に使用され、それまでの RNN を用いた手法等に比べて、精度・学習コストの両面でより良い性能が出ました。

Transformer の概要図を以下に示します。大きな縦長のブロックのようなものが2つ並んでいて、左の方の先から右の方の真ん中あたりに矢印が伸びているのが分かると思います。この構造は「Encoder-Decoder モデル」と言い、ざっくり説明すると、例えばフランス語の文章を英語の文章に翻訳する場合、左のブロック(Encoder)でフランス語から「意味」にエンコードし、右のブロック(Decoder)で「意味」から英語にデコードする、といった感じで使われます。

今回紹介する ViT モデルは、この左側の部分、すなわちエンコーダ部分のみをほぼそのまま利用したモデルとなっています。（1枚目の画像の右側の図と見比べると、かなり似ています。）

（以降では、ViT の理解に必要なエンコーダの部分についてしか解説しないので、Transformer の全体像について知りたい方はこちらの記事などを参照してください。）

ViT とは

そんな Transformer のエンコーダの部分を画像認識に応用したものが ViT です。

特徴

• SoTA を上回る精度
• 畳み込みを行わないモデル
• それまでの SoTA の約$\frac{1}{15}$倍の計算コスト

モデル概要

画像が入力されてから、認識結果が出力されるまでの流れをざっくりと説明すると、

1. 画像がパッチに分割されて
2. 各パッチがベクトルに変換されて
3. その先頭に [class] トークンを付加したものに位置エンコーディングが加算されて
4. それらが Transformer Encoder によって処理されて
5. その出力の0番目のベクトルが MLP Head で処理されて

最終的にクラスの出力が得られます。では、具体的なアルゴリズムと実装について、各ステップ毎に、次の章で見ていきます。

ViT を作る

まず最初に、実装の全体像を眺めます。コードの量が増えてしまうので、ViT 以外の class の実装は一旦隠しておきます。class ViT の forward 内を見てもらうと、入力画像 img に対して、上で説明した処理を行なっているのが分かると思います。

vit_model.py

import torch
import torch.nn as nn

from einops import repeat
from einops.layers.torch import Rearrange


class Patching(nn.Module):
    # 後ほど解説

class LinearProjection(nn.Module):
    # 後ほど解説

class Embedding(nn.Module):
    # 後ほど解説

class MLP(nn.Module):
    # 後ほど解説

class MultiHeadAttention(nn.Module):
    # 後ほど解説

class TransformerEncoder(nn.Module):
    # 後ほど解説

class MLPHead(nn.Module):
    # 後ほど解説

class ViT(nn.Module):
    def __init__(self, image_size, patch_size, n_classes, dim, depth, n_heads, channels = 3, mlp_dim = 256):
        """ [input]
            - image_size (int) : 画像の縦の長さ（= 横の長さ）
            - patch_size (int) : パッチの縦の長さ（= 横の長さ）
            - n_classes (int) : 分類するクラスの数
            - dim (int) : 各パッチのベクトルが変換されたベクトルの長さ（参考[1] (1)式 D）
            - depth (int) : Transformer Encoder の層の深さ（参考[1] (2)式 L）
            - n_heads (int) : Multi-Head Attention の head の数
            - chahnnels (int) : 入力のチャネル数（RGBの画像なら3）
            - mlp_dim (int) : MLP の隠れ層のノード数
        """

        super().__init__()
        
        # Params
        n_patches = (image_size // patch_size) ** 2
        patch_dim = channels * patch_size * patch_size
        self.depth = depth

        # Layers
        self.patching = Patching(patch_size = patch_size)
        self.linear_projection_of_flattened_patches = LinearProjection(patch_dim = patch_dim, dim = dim)
        self.embedding = Embedding(dim = dim, n_patches = n_patches)
        self.transformer_encoder = TransformerEncoder(dim = dim, n_heads = n_heads, mlp_dim = mlp_dim, depth = depth)
        self.mlp_head = MLPHead(dim = dim, out_dim = n_classes)


    def forward(self, img):
        """ [input]
            - img (torch.Tensor) : 画像データ
                - img.shape = torch.Size([batch_size, channels, image_height, image_width])
        """

        x = img

        # 1. パッチに分割
        # x.shape : [batch_size, channels, image_height, image_width] -> [batch_size, n_patches, channels * (patch_size ** 2)]
        x = self.patching(x)

        # 2. 各パッチをベクトルに変換
        # x.shape : [batch_size, n_patches, channels * (patch_size ** 2)] -> [batch_size, n_patches, dim]
        x = self.linear_projection_of_flattened_patches(x)

        # 3. [class] トークン付加 + 位置エンコーディング 
        # x.shape : [batch_size, n_patches, dim] -> [batch_size, n_patches + 1, dim]
        x = self.embedding(x)

        # 4. Transformer Encoder
        # x.shape : No Change
        x = self.transformer_encoder(x)

        # 5. 出力の0番目のベクトルを MLP Head で処理
        # x.shape : [batch_size, n_patches + 1, dim] -> [batch_size, dim] -> [batch_size, n_classes]
        x = x[:, 0]
        x = self.mlp_head(x)

        return x

次に、各処理について詳しく説明していきます。

（※注意：本実装では dropout は入れていません。）

変数

変数	コード中変数名	意味等
$H$	image_size	画像の縦の長さ
$W$	image_size	画像の横の長さ（本実装では $H = W$ ）
$B$	batch_size	バッチサイズ
$P$	patch_size	パッチのサイズ（縦の長さ、および、横の長さ）
$C$	channels	チャンネル数（RGB 画像の場合 $C=3$）
$D$	dim	パッチベクトル変換後のベクトルの長さ
$N$	n_patches	パッチの数

1. パッチに分割

class Patching(nn.Module):
    def __init__(self, patch_size):
        """ [input]
            - patch_size (int) : パッチの縦の長さ（=横の長さ）
        """
        super().__init__()
        self.net = Rearrange("b c (h ph) (w pw) -> b (h w) (ph pw c)", ph = patch_size, pw = patch_size)
    
    def forward(self, x):
        """ [input]
            - x (torch.Tensor) : 画像データ
                - x.shape = torch.Size([batch_size, channels, image_height, image_width])
        """
        x = self.net(x)
        return x

まず、入力画像をパッチに分割するステップについて解説します。とは言いつつもそんなに難しいことはしていなくて、一枚の画像を複数枚のパッチ（上の例だと9枚）に切り分けて、左上から横に並べていくだけです。

注意点としては、元の画像は $[C, H, W]$ の3次元配列だったのに対し、切り分けた後のパッチのベクトルは $C\cdot P^2$ の1次元配列になっているということです。従って、コード中の x のサイズは

• $[B, C, H, W] → [B, N, C\cdot P^2]$

というように変形されます。

2. 各パッチをベクトルに変換

class LinearProjection(nn.Module):
    def __init__(self, patch_dim, dim):
        """ [input]
            - patch_dim (int) : 一枚あたりのパッチの次元（= channels * (patch_size ** 2)）
            - dim (int) : パッチが変換されたベクトルの次元 
        """
        super().__init__()
        self.net = nn.Linear(patch_dim, dim)

    def forward(self, x):
        """ [input]
            - x (torch.Tensor) 
                - x.shape = torch.Size([batch_size, n_patches, patch_dim])
        """
        x = self.net(x)
        return x

次に、各パッチのベクトルを別サイズのベクトルに変換するステップについて解説します。以下の文字を用いて説明します。

• $\mathbf{x}^k_p \in \mathbb{R}^{(P^2\cdot C)}$ : $k$ $(1\leq k \leq N)$ 個目のパッチのベクトル

また、各パッチのベクトルの長さ（コード中「patch_dim」）は $C\cdot P^2$ となります。

実装方法としては、$(C\cdot P^2) \times D$ の行列 $\mathbf{E}$ を用いて、$\mathbf{x}^k_p \mathbf{E}$ といった具合に変換します。$\mathbf{E}$ はコード中では「nn.Linear」の部分で、この行列自体も学習可能なパラメータです。

3. [class] トークン付加 + 位置エンコーディング

class Embedding(nn.Module):
    def __init__(self, dim, n_patches):
        """ [input]
            - dim (int) : パッチが変換されたベクトルの次元
            - n_patches (int) : パッチの枚数
        """
        super().__init__()
        # class token
        self.cls_token = nn.Parameter(torch.randn(1, 1, dim))

        # position embedding
        self.pos_embedding = nn.Parameter(torch.randn(1, n_patches + 1, dim))
    
    def forward(self, x):
        """[input]
            - x (torch.Tensor)
                - x.shape = torch.Size([batch_size, n_patches, dim])
        """
        # バッチサイズを抽出
        batch_size, _, __ = x.shape

        # [class] トークン付加
        # x.shape : [batch_size, n_patches, patch_dim] -> [batch_size, n_patches + 1, patch_dim]
        cls_tokens = repeat(self.cls_token, "1 1 d -> b 1 d", b = batch_size)
        x = torch.concat([cls_tokens, x], dim = 1)

        # 位置エンコーディング加算
        x += self.pos_embedding

        return x

「2. 各パッチをベクトルに変換」によって作られた $N$（コード中「n_patches」）個のパッチのベクトル達の先頭に [class] トークンを付加します。これは学習可能なパラメータで、Transformer Encoder によって処理された後の [class] トークンに対応する部分（正確にはそれを nn.Linear(dim, n_classes) で処理したもの）が、予測結果を返してくれます。

この時点で、x のサイズは [$B$, $N \color{red}{+1}$, $D$] となりました（[class] トークンの分）。

その後、位置エンコーディングを行います。後ほど説明する Transformer Encoder では、入力トークンの位置情報を把握することができないため、位置情報をあらかじめ付加する必要があります。実装としては、$(N+1)\times D$ の行列 $\mathbf{E}_{pos}$ を加算します。これは、学習可能なパラメータです。

1~3 のまとめ

ここまでの処理をまとめます。まず最初に、画像を $N$ 個のパッチに分割しました。パッチ 1 つのベクトル $\mathbf{x}_p$ の長さは $C\cdot P^2$ で、これが $N$ 個並んだ $[\mathbf{x}^1_p; \mathbf{x}^2_p; \cdots ; \mathbf{x}^N_p]$ という形になっています。

その後、各パッチのベクトルを長さ $D$ のベクトルに変換し、$[\mathbf{x}^1_p\mathbf{E}; \mathbf{x}^2_p\mathbf{E}; \cdots ; \mathbf{x}^N_p\mathbf{E}]$ となります。

最後に、 [class] トークンを付加してから位置エンコーディングを行い、最終的に Transformer Encoder への入力 $\mathbf{z}_0$ は以下のようになります。

\mathbf{z}_0 = [\mathbf{x}_{class}; \mathbf{x}^1_p\mathbf{E}; \mathbf{x}^2_p\mathbf{E}; \cdots ; \mathbf{x}^N_p\mathbf{E}] + \mathbf{E}_{pos}

4. Transformer Encoder

class TransformerEncoder(nn.Module):
    def __init__(self, dim, n_heads, mlp_dim, depth):
        """ [input]
            - dim (int) : 各パッチのベクトルが変換されたベクトルの長さ（参考[1] (1)式 D）
            - depth (int) : Transformer Encoder の層の深さ（参考[1] (2)式 L）
            - n_heads (int) : Multi-Head Attention の head の数
            - mlp_dim (int) : MLP の隠れ層のノード数
        """
        super().__init__()

        # Layers
        self.norm = nn.LayerNorm(dim)
        self.multi_head_attention = MultiHeadAttention(dim = dim, n_heads = n_heads)
        self.mlp = MLP(dim = dim, hidden_dim = mlp_dim)
        self.depth = depth

    def forward(self, x):
        """[input]
            - x (torch.Tensor)
                - x.shape = torch.Size([batch_size, n_patches + 1, dim])
        """
        for _ in range(self.depth):
            x = self.multi_head_attention(self.norm(x)) + x
            x = self.mlp(self.norm(x)) + x

        return x

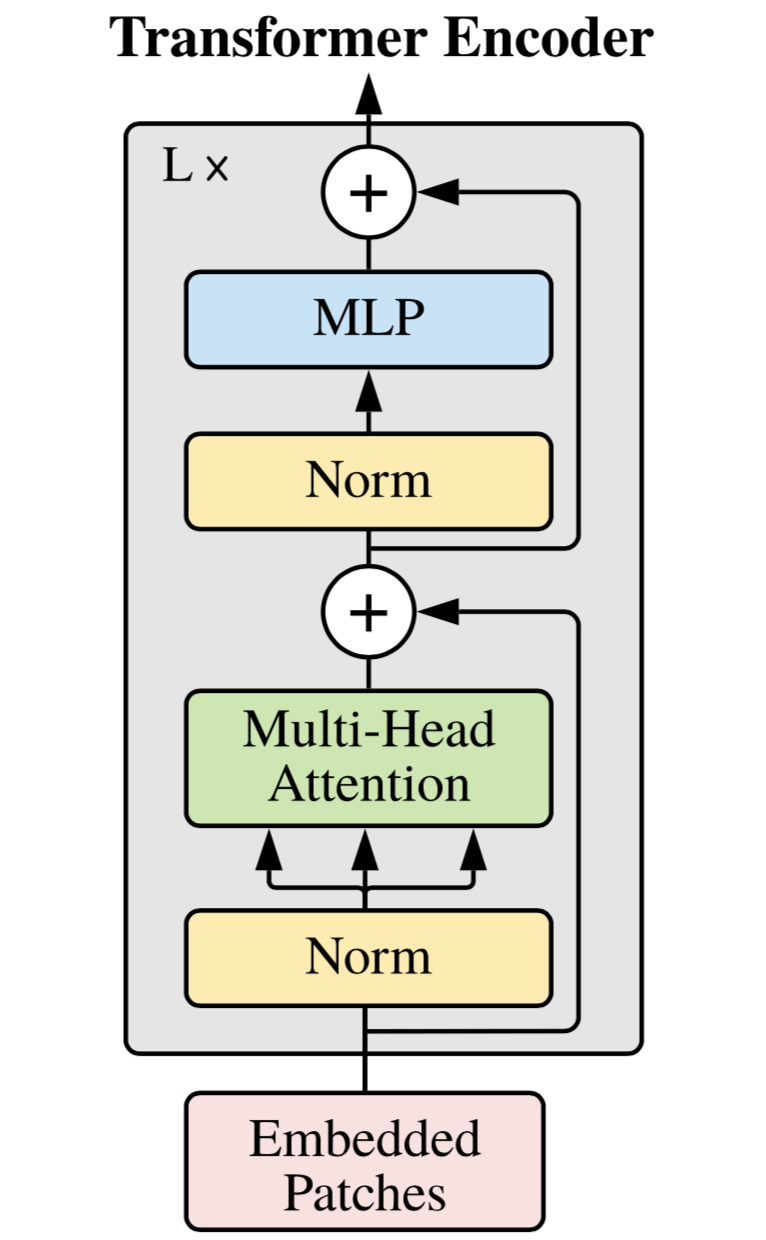
いよいよ Transformer Encoder の解説です。Transformer Encoder は大きく分けて以下の 4 つの要素から構成されます。

• 残差接続（上の画像の $\oplus$ ）
• Layer Normalization（上の画像の Norm ）
• Multi-Head Self-Attention（上の画像の Multi-Head Attention ）
• Multi Layer Perceptron（上の画像の MLP ）

Layer Normalization を $LN$、Multi-Head Self-Attention を $MSA$、Multi Layer Perceptron を $MLP$ とすると、以下の式のようになります。

\begin{align}
\mathbf{z}'_l &= MSA(LN(\mathbf{z}_{l-1})) + \mathbf{z}_{l-1} & (l&=1, \dots , L)\\
\mathbf{z}_{l} &= MLP(LN(\mathbf{z}'_l )) + \mathbf{z}'_l & (l&=1, \dots , L)\
\end{align}

以下では、それぞれの要素について見ていきます。

残差接続

残差接続は、ViT 以外でも広く使われる残差学習のためのパーツです。これによって、層を深くした場合に発生する

• 劣化問題
• 収束の遅さ

が解決されます。

（詳細を知りたい方は、こちらの記事やこちらの論文を参照するか、「ResNet」で検索して見てください。）

Layer Normalization

これも、ViT 以外にも広く使われる一般的な仕組みで、実装も「nn.LayerNorm」で簡単に実装できるので、説明は割愛します。

（詳細を知りたい方は、こちらの記事やこちらの論文を参照するなどしてください。）

Multi-Head Attention

class MultiHeadAttention(nn.Module):
    def __init__(self, dim, n_heads):
        """ [input]
            - dim (int) : パッチのベクトルが変換されたベクトルの長さ
            - n_heads (int) : heads の数
        """
        super().__init__()
        self.n_heads = n_heads
        self.dim_heads = dim // n_heads

        self.W_q = nn.Linear(dim, dim)
        self.W_k = nn.Linear(dim, dim)
        self.W_v = nn.Linear(dim, dim)

        self.split_into_heads = Rearrange("b n (h d) -> b h n d", h = self.n_heads)

        self.softmax = nn.Softmax(dim = -1)

        self.concat = Rearrange("b h n d -> b n (h d)", h = self.n_heads)

    def forward(self, x):
        """[input]
            - x (torch.Tensor)
                - x.shape = torch.Size([batch_size, n_patches + 1, dim])
        """
        q = self.W_q(x)
        k = self.W_k(x)
        v = self.W_v(x)

        q = self.split_into_heads(q)
        k = self.split_into_heads(k)
        v = self.split_into_heads(v)

        # Logit[i] = Q[i] * tK[i] / sqrt(D) (i = 1, ... , n_heads)
        # AttentionWeight[i] = Softmax(Logit[i]) (i = 1, ... , n_heads)
        logit = torch.matmul(q, k.transpose(-1, -2)) * (self.dim_heads ** -0.5)
        attention_weight = self.softmax(logit)

        # Head[i] = AttentionWeight[i] * V[i] (i = 1, ... , n_heads)
        # Output = concat[Head[1], ... , Head[n_heads]]
        output = torch.matmul(attention_weight, v)
        output = self.concat(output)
        return output

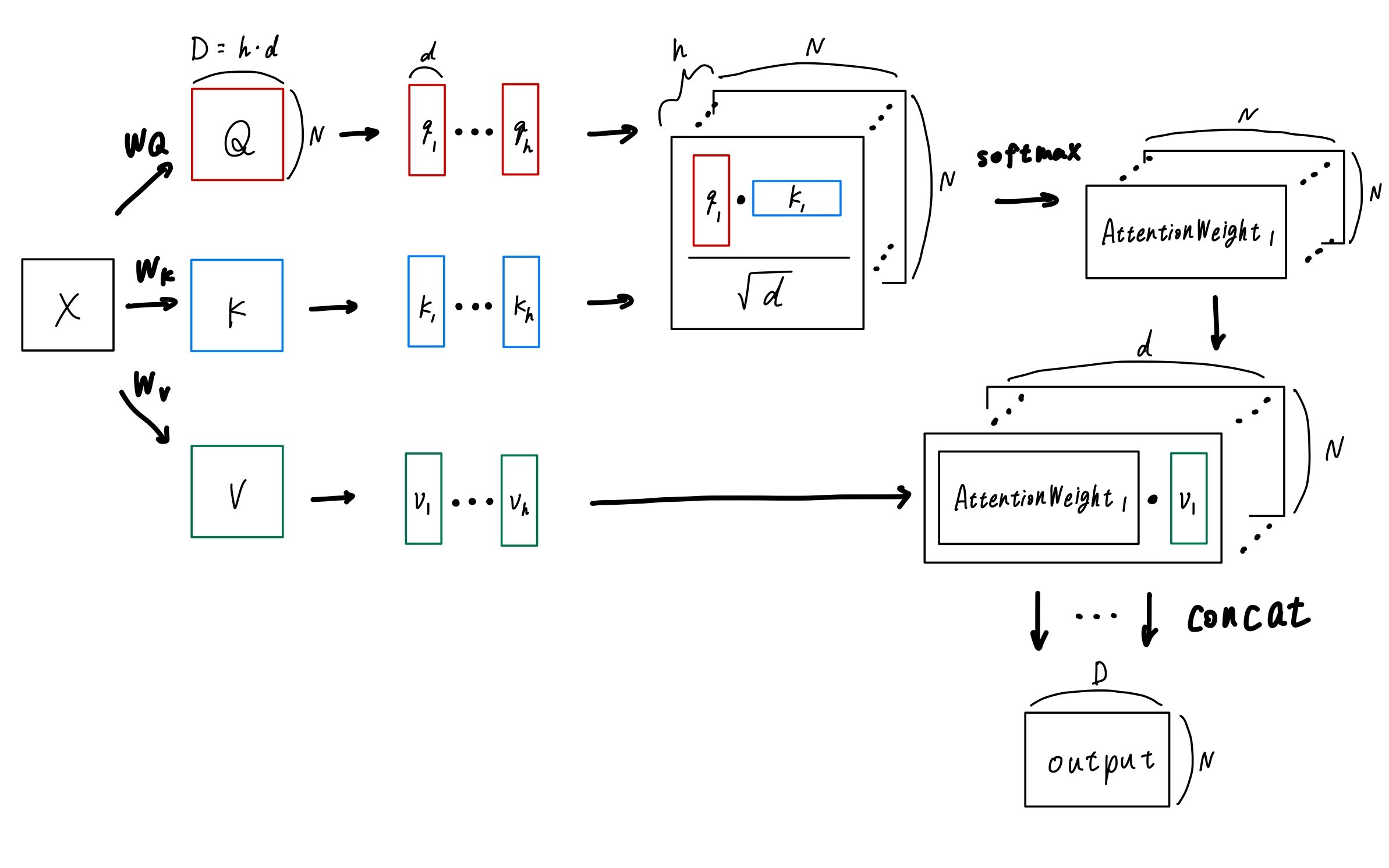
Multi-Head Attention は、Transformer の要となる非常に重要なブロックです。

（この記事では、Multi-Head Attention の「お気持ち」的な部分は説明せず、実装に焦点を当てて説明するので、そもそも Multi-Head Attention が何なのか分からないという方は、先にこちらの動画の15:40~を観ることをお勧めします。）

変数	コード中変数名	意味等
$h$	n_heads	head の数
$d$	dim_heads	1 つの head のベクトルの長さ($d = D / h$)

まず、入力 $\mathbf{x}$ に $D\times D$ の正方行列 $\mathbf{W}_Q, \mathbf{W}_K, \mathbf{W}_V$ をかけて、それぞれ $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ を作ります（各 $\mathbf{W}$ は学習可能なパラメータです）。

\begin{align}
\mathbf{Q} & = \mathbf{x}\mathbf{W}_Q \\
\mathbf{K} & = \mathbf{x}\mathbf{W}_K \\
\mathbf{V} & = \mathbf{x}\mathbf{W}_V
\end{align}

その後、$\mathbf{Q}, \mathbf{K}, \mathbf{V}$ をそれぞれ $h$ 個に切り分け、$[\mathbf{q}_1, ... , \mathbf{q}_h], [\mathbf{k}_1, ... , \mathbf{k}_h], [\mathbf{v}_1, ... , \mathbf{v}_h]$ とします。$\mathbf{q}_1$ 等のサイズが $N\times d$ であることに注意してください。

その後、各 $i (=1, ... ,h)$ について、$\mathbf{head}_i$ を以下の式で計算します。

\mathbf{head}_i = softmax\left(\frac{\mathbf{q}_i\mathbf{k}^T_i}{\sqrt{d}}\right)\mathbf{v}_i

最後に、$[\mathbf{head}_1, ... ,\mathbf{head}_h]$ を結合して、出力とします。

MLP

class MLP(nn.Module):
    def __init__(self, dim, hidden_dim):
        """ [input]
            - dim (int) : パッチのベクトルが変換されたベクトルの長さ
            - hidden_dim (int) : 隠れ層のノード数
        """
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(dim, hidden_dim),
            nn.GELU(),
            nn.Linear(hidden_dim, dim)
        )

    def forward(self, x):
        """[input]
            - x (torch.Tensor)
                - x.shape = torch.Size([batch_size, n_patches + 1, dim])
        """
        x = self.net(x)
        return x

ここはあまり解説することはなく、コードの通りです。

5. MLP Head

MLP Head クラス

class MLPHead(nn.Module):
    def __init__(self, dim, out_dim):
        super().__init__()
        self.net = nn.Sequential(
            nn.LayerNorm(dim),
            nn.Linear(dim, out_dim)
        )
    
    def forward(self, x):
        x = self.net(x)
        return x

ViT クラス側

    x = x[:, 0]
    x = self.mlp_head(x)

Transformer Encoder で処理された後の [class] トークンに対応する部分を MLP Head で処理します。具体的には、最初に Layer Norm で処理し、その後、クラスの数の長さのベクトルに線形で変換します。

ViT を使ってみる

torchvision.datasets.CIFAR10 で学習・検証してみました。こちらの ipynb を上からポチポチしてもらえばできるかと思います。結果としては、過学習気味ではあるものの（dropout を入れてないせいだと思う）、一応ちゃんと学習が進んではいるようでした。

おわりに

間違い等ありましたら、指摘していただけると助かります。また、pip install で使える公式の(?)実装もご参照ください。