RNNの一種で,バックプロパゲーションを使わずに軽快に時系列処理の学習ができる枠組みであるReservoir computing モデルを TensorFlow2を使って実装しみました.
細かい部分の実装はそれほど美しくない気がしますが,とりあえず参考になるかと思うので公開しておきます.
ある程度TensorFlow2 のモデルの書き方に慣れてきた人が対象です.
JaegerらのEcho State Network を作ってみます.
モデル
ネットワークは内部状態$x_t \in R^{N}$ を持ち,その状態は次式で更新されます
x_{t+1} = \tanh(Wx_{t}+ W_{in}u_{t} + W_{fb} z_{t} )
ここで $u_{t} \in R^{N_{in}}$は入力,$z_{t} \in R^{N_{out}}$は出力, $W$は$(N\times N)$のリカレント結合の行列,$W_{in}$は$(N\times N_{in})$の入力重み行列, $W_{fb}$は$(N \times N_{out})$ の出力をフィードバックする重み行列です.
各時刻は出力は内部状態の線形の重み付き和でとります.
z_{t} = W_{out} x_{t}
ここで$W_{out}$は$(N_{out}\times N)$ の出力重み行列です.
学習の手順
タスクや研究目的によって細かい設定が違いますが,元の論文にある時系列予測/生成をする場合を考えます.教師信号を$d_{t} \in R^{N_{out}}$とします.
オリジナルのEcho State Networkでは,学習期間では,状態更新式の$z_{t}$ に実際の出力を入れる代わりに,正しい出力$d_{t}$をいれて状態更新を繰り返します.訓練期間を時刻$(t_1, ..., t_{T})$の間とすると,状態更新を時刻$t_T$まで繰り返した後で,その間の内部状態$\{x_{t_{1}},..., x_{t_T} \}$と,時刻の正解出力 $\{d_{t_{1}}, ..., d_{t_T}\}$ をもとに,重み$W_{out}$を線形回帰やリッジ回帰により求めます.
最急降下法は利用せず,行列の計算で学習が実現できます.リッジ回帰の場合,以下の式で($N_{out} \times N$)の出力重み行列$W_{out}$ を決定します.
W_{out}= (X^{T}X + \lambda I )^{-1}X^{T}d
$X$ は$ x_{t_1},..., x_{t_T}$ を転置して縦に積んだデータ行列($T\times N$), $d=(d_{t_1},d_{t_2}, ..., d_{t_N})^{T}$は正解の行列 ($T\times N_{out}$), $I$は単位行列です. $\lambda$ は重みの大きさに対するペナルティの強さを決める係数です.
テスト区間(時系列生成)
テスト時には正解出力をフィードバックにいれるかわりに,モデル自身の出力をフィードバック入力に入れ,1ステップ先の信号を予測することを繰り返します.この繰り返しにより次々に信号を生成することを行い,誤差などを評価します.
今回は訓練区間が終わった直後に,内部状態はそのまま,テスト区間にはいります.
実装
方針
-
keras.layersに用意されているRNNレイヤーを使う - 出力$z$を入力に戻す部分があり,学習時はここに正解信号を入れるので,切り替えが必要.これらができるよう,RNNのダイナミクスを指定する
cellは自作のものを使う. - 学習はBackpropではなく,論文と同じように反復を必要としない回帰で行う. (backpropによる学習と比較できるようにはしたい)
参考にした公式ガイドなど
Kerasを使用したリカレントニューラルネットワーク(RNN)
tf.keras.layers.RNN
コード
準備
倍精度を使います.単精度ではこの条件での学習に失敗していました.
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras.layers import Layer, Dense, RNN
from tensorflow.keras import Model
import time
tf.keras.backend.set_floatx('float64')
mydtype = tf.float64
確率$p$で結合が存在するスパースなリカレント結合行列を作り,$g/\sqrt(Np)$を掛けて重みのスケーリングを行う処理を, initializerの仕組みで行うためのクラスを作っておきます. $g$は全体の結合強度を決めるスケーリング係数で,入力が無い場合のダイナミクスが安定なのか,カオス的になるのかをこの値で調整できます.
class SparseWeightInitializer():
'''
p_connect の確率で結合する行列を作り,重みは正規分布からとり,最後にスケーリングする処理を
初期化時に行うためのinitializerクラス
'''
def __init__(self, p_connect, g_scale):
self.p_connect = p_connect
self.g_scale = g_scale
def __call__(self, shape, dtype=mydtype):
c = tf.cast(tf.random.uniform(shape, dtype=dtype)
< self.p_connect, mydtype)
w = c*tf.random.normal(shape, dtype=dtype)
w = tf.constant(self.g_scale, dtype=mydtype) * w / \
tf.math.sqrt(tf.constant(self.p_connect, dtype=mydtype)*shape[0])
return w
cell のクラス
RNNの1ステップの処理を行う部分となるcellを,kerasのレイヤーとして作ります.1回の状態更新の入力から出力までを計算する部分です.
initとbuildでは,更新式や出力の式にでてくる重みのそれぞれ,つまり入力の重み層,リカレント結合層,出力の重み層,フィードバックの重み層の4つをDense層として準備しています.
cellのcallは入力と,内部状態を受け取り,出力と更新された内部状態を返すように設計するものです.今回はモデルの学習のために,(一般的には内部状態とよばれる)$x_{t}$ も出力に含めます.逆に,フィードバックに使うために, (一般的には出力とよばれる)$z_t$も内部状態として保存しておく必要があるため,内部状態に含めました.すこし不自然ですが,このため,callの返り値は出力として[z,x], 内部状態として[z,x]というように,どちらも二つの変数のリストを返すようにしました.
callの中で,モデルのところに書いた状態更新の式と出力の式が実装されていることをみてください.
また,前述のように,ESNではフィードバックに正解の信号を入れる場合と,自身の出力を入れる場合で切り替える必要があるので, self.fb_mode をフラグとしてcall内で処理を切り替えています.
class ReservoirCell(Layer):
def __init__(self, N, N_out, N_in=1, fb_mode=False, p_connect=0.1, g_scale=1.0, w_fb_max=1.0, s_noise=0,
**kwargs):
# fbmode is on, it acts in self-feedback mode, otherwise, receive teacher signal
# instead of self-feedback
# p_connect: probability of connection
# g_scaling : scaling coefficient that controll recurrent weight strength
self.state_size = [tf.TensorShape([N]), tf.TensorShape(
[N_out])] # この二つはRNNCellに設定しておくことが求められている
self.output_size = [tf.TensorShape([N]), tf.TensorShape([N_out])]
self.N = N
self.N_out = N_out
self.N_in = 1
self.fb_mode = fb_mode
self.p_connect = p_connect
self.g_scale = g_scale
self.s_noise = s_noise # noise
sparse_initializer = SparseWeightInitializer(
self.p_connect, self.g_scale) # initializer for Recurrent connection
# それぞれの結合をLayerとして定義.固定する重みはtrainable=Falseにしておく
#リカレント結合
self.sum_rec = Dense(N, activation=None, use_bias=True, kernel_initializer=sparse_initializer,
bias_initializer='zeros', trainable=False, dtype=mydtype)
#入力層
self.sum_in = Dense(N, activation=None, use_bias=False,
kernel_initializer=tf.keras.initializers.RandomUniform(minval=-0.5, maxval=0.5), trainable=False,
dtype=mydtype)
#フィードバック層
self.sum_fb = Dense(N, activation=None, use_bias=True,
kernel_initializer=tf.keras.initializers.RandomUniform(minval=-w_fb_max, maxval=w_fb_max), trainable=False,
dtype=mydtype)
#活性化関数
self.act = tf.keras.layers.Activation('tanh')
# 出力層
self.z = Dense(N_out, activation=None, use_bias=True, kernel_initializer='glorot_uniform',
bias_initializer='zeros', trainable=True, dtype=mydtype)
super(ReservoirCell, self).__init__(**kwargs)
def build(self, input_shape):
# expect input_shape to contains (batch, dim_input_1)
# build each connections
#self.N_in = input_shape[0]
print('cell was build')
self.sum_rec.build(input_shape=[None, self.N])
self.sum_in.build(input_shape=[None, self.N_in])
self.sum_fb.build(input_shape=[None, self.N_out])
self.act.build(input_shape=[None, self.N])
self.z.build(input_shape=[None, self.N])
def call(self, inputs, states, training=None):
# inputs should be in shape [(batch, N_in),(batch, N_out)]
# states should be in shape [(batch,N), (batch,N_out)]
inputs, teacher_fb = tf.nest.flatten(inputs)
x, z = states
#print(z.shape)
if self.fb_mode: # self-feedback mode
fb = self.sum_fb(z)
#print('fb-mode')
else: # use external signal for feedback term
fb = self.sum_fb(teacher_fb)
#print('non-fb-mode')
x = self.act(self.sum_rec(x) + self.sum_in(inputs) + fb +
self.s_noise * tf.random.uniform(x.shape, dtype=mydtype))
z = self.z(x)
#print(x.shape)
#print(z.shape)
return [x, z], [x, z]
def get_config(self):
return {"N": self.N, "N_out": N_out, "N_in": self.N_in}
def set_fb_mode(self, fb_mode=True):
''' 外からフィードバック部へ入力するか,自身の出力をフィードバックするかのフラグを設定'''
self.fb_mode = fb_mode
モデルの作成
定義したcellを利用するRNNクラスのLayerを作り,これをもとにModelを作ります.RNNクラスは内部状態の初期値等の管理や,時間ステップ分連続して計算し,出力を出すなどの処理ができます.タスクの性質から,毎時刻の出力や内部状態が必要ですので,RNNを作る時にreturn_sequence=Trueにします.またstateful=Trueにします.
class RSVModel(Model):
'''
reservoir RNN model
'''
def __init__(self, N, N_out=1, N_in=1, batch_size=1, fb_mode=False, p_connect=0.1, g_scale=1.2,
w_fb_max=1, s_noise=0, name='reservoir'):
'''
fb_mode: True if using true feedback
p_connect: connection probability of recurrent weight matrix
g_scale: scaling factor of recurrent weight matrix
w_fb_max: max of feedback weight
s_noise: noise amplitude
'''
super(RSVModel, self).__init__()
self.rsvcell = ReservoirCell(N, N_out, N_in=N_in, fb_mode=fb_mode,
p_connect=p_connect, g_scale=g_scale, w_fb_max=w_fb_max, s_noise=s_noise,
)
self.rsvlayer = RNN(self.rsvcell, return_sequences=True,
stateful=True, name='rnnlayer')
def call(self, inputs):
inputs, fb = inputs
return self.rsvlayer((inputs, fb))
モデルを作成する関数を作っておきます.
Model-RNNレイヤー-RNNセル-各重み層 と多段の入れ子になってて少しわかりにくいので,関数の最後のところでは,外部から呼び出したいテンソル等を簡単に参照できるように,モデルに直接属性を追加しています.
def create_reservoir_model(N, N_in, N_out,
batch_size=1, fb_mode=False, p_connect=0.1, g_scale=1.2,
initial_state=None, w_fb_max=1.0, s_noise=0.0, name='reservoir'):
model = RSVModel(N=N, N_in=N_in, N_out=N_out, fb_mode=fb_mode,
p_connect=p_connect, g_scale=g_scale, w_fb_max=w_fb_max, s_noise=s_noise, name=name)
inp = np.zeros((batch_size, 100, N_in), dtype=np.float64)
z = np.zeros((batch_size, 100, N_out), dtype=np.float64)
model([inp, z]) # build
if initial_state is not None:
model.rsvlayer.reset_states(initial_state)
model.W_rec = model.rsvcell.sum_rec.kernel
model.W_out = model.rsvcell.z.kernel
model.W_in = model.rsvcell.sum_in.kernel
model.bias_out = model.rsvcell.z.bias
model.set_fb_mode = model.rsvcell.set_fb_mode
model.N_out = N_out
model.N_in = N_in
model.N = N
# ここで訓練用変数のリストをつくっておく.
model.train_variables = [model.W_out, model.rsvcell.z.bias]
return model
重みの更新
重みを更新する部分です. tf.linalg.pinvで疑似逆行列を使って重みを求めています.
def update_weight(model, t_learn, teacher_signal, xt, lambda_ridge=0.001):
len_t = len(t_learn)
batch_size = xt.shape[0]
#print(batch_size)
#print(len_t)
#print(t_learn[-1])
#get learning period and expand batches
target = np.reshape(teacher_signal[:, t_learn, :], [
batch_size*len_t, model.N_out])
assert target.shape == (batch_size*len_t, model.N_out)
X = xt[:, t_learn[0]:(1+t_learn[-1]), :] # data matrix X
X = tf.reshape(X, [X.shape[0]*X.shape[1], X.shape[2]]) # expanding batches
# add a column filled with 1 for the bias term
o = tf.ones([batch_size*len_t, 1], dtype=mydtype)
X = tf.concat([X, o], axis=1)
assert X.shape == (batch_size * len(t_learn), N+1)
XT = tf.transpose(X, [1, 0])
w_new = tf.linalg.pinv(XT @ X + lambda_ridge *
tf.linalg.eye(model.N+1, dtype=mydtype)) @ XT @ target
model.W_out.assign(w_new[0:-1, :])
model.bias_out.assign(w_new[-1, :])
return w_new
実行する関数
用意した入力を入れて,RNNを動かす関数です.フィードバックを外から入れる場合と,自身の出力をフィードバックする場合で2通り作っておきます.
@tf.function
def gen_sequence_w_external_fb(model, input_signal, fb_signal):
'''
外部からフィードバックに信号をいれてRNNを動かす
'''
model.set_fb_mode(False)
xt, zt = model([input_signal, fb_signal])
return xt, zt
@tf.function
def gen_sequence_w_internal_fb(model, input_signal):
'''
自身のフィードバック信号を使ってRNNを動かす
'''
model.set_fb_mode(True)
dummy = tf.zeros(shape=[input_signal.shape[0],
input_signal.shape[1], model.N_out], dtype=tf.float64)
xt, zt = model([input_signal, dummy])
return xt, zt
教師信号(正弦波)を作る関数です.
def periodic_signal(length, freq=1.0/1200.0, amp=1.3):
'''
makes sinusoidal teacher signal
args:
freq: base frequency
amp: amplitude
'''
ft = (amp/1.0)*np.sin(2.0*np.pi*freq*np.arange(length))
return np.reshape(ft, [length, 1])
タスクの実行例
やや簡単ですが,正弦波信号を教師信号として,その1ステップ先の予測を行う学習を行い,学習後はフィードバックを利用して時系列生成を行います. 外部入力$u$は今回使わず常に0のままです.
レザバーの初期化と教師信号の作成
# %% create model
N = 1000
N_in = 1
N_out = 1
p_connect = 0.05
g_scale = 0.6
lambda_ridge = 1e-5
model = create_reservoir_model(
N, N_in, N_out, p_connect=p_connect, g_scale=g_scale, w_fb_max=0.3, s_noise=1e-8)
# %% prepare input signal
batch_size = 1
total_time = 10000
timestep_learning = 5000
timestep_test = 5000
t_learn = np.arange(2000, 5000)
period = 240.0
split_length = 200
input_signal = np.zeros((1, timestep_learning, N_in)) # do not use
# 教師信号
# 正弦波を作って(batch, timestep, 1) にreshape
target_signal = periodic_signal(
total_time+1, freq=1/period, amp=1.0).reshape([1, -1, 1])
# 訓練期間の信号
target_signal_learning = target_signal[:, 0:timestep_learning, :]
fb_signal = target_signal_learning
teacher_signal = target_signal[:, 1:(timestep_learning+1), :] # 次のステップの予測
input_signal_test = np.zeros((1, timestep_test, N_in))
target_signal_test = target_signal[:, timestep_learning:, :] # テスト区間での目標信号
teacher_signal_test = target_signal_test[:, 1:, :] # 正解
訓練区間
訓練期間は外から正解をフィードバック項$z_t$ に入れます.
startt = time.time()
xt_learn, zt_learn = gen_sequence_w_external_fb(model, input_signal, fb_signal)
print(f'elapsed_time={time.time()-startt}')
重み更新
訓練区間の内部状態と正解信号を使って重み更新を行います.
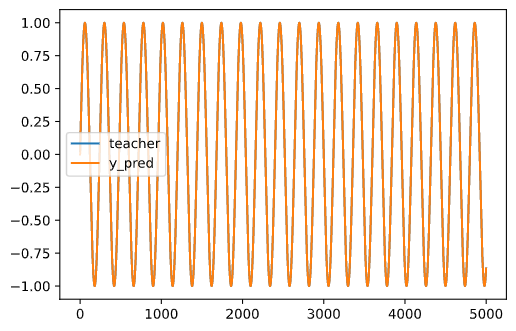
y_pred 以下の行は,回帰により訓練期間の学習が成功しているかみているだけで,省略しても問題ありません.
# update weight
w_new = update_weight(model, t_learn, teacher_signal,
xt_learn, lambda_ridge=lambda_ridge)
plt.plot(teacher_signal[0,:,0], label='teacher')
plt.plot(y_pred[0, :, 0], label='y_pred')
plt.legend()
plt.show()
テスト区間
# %% sequence generation
# 最後の出力を学習後の値で修正して,最初から正しいフィードバックが与えられるようにする.
z_mod = model.rsvcell.z(xt_learn[:, -1, :])
model.rsvlayer.reset_states([xt_learn[:, -1, :], z_mod])
# %% テスト区間(自己フィードバックにより時系列生成
model.set_fb_mode(True)
startt = time.time()
xt_test, zt_test = gen_sequence_w_internal_fb(model, input_signal_test)
# %%
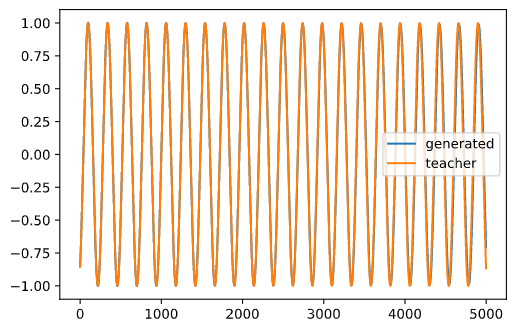
plt.plot(range(timestep_test), zt_test[0, :, 0], label='generated')
plt.plot(range(timestep_test), teacher_signal_test[0, :, 0], label='teacher')
plt.legend()
plt.show()
正解(教師信号)とレザバーが生成した信号が重なっており,学習が成功したことがわかります.
学習後に学習前の最後の出力を修正後の重みを使って修正することを行っていないと,うまくいかないことがありました.