LoginSignup
7
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@yymgt(やまぐち ゆたか)

TensorFlowで力学系(3) Lyapunov 指数の計算

Last updated at Posted at 2019-10-13

力学系の軌道不安定性を表す指標として　Lyapunov 指数があります。
常微分方程式で定義された力学系において TensorFlow を使って最大 Lyapunov 指数を求めます。

  • まだ TensorFlow 1.14 を使用中です。
  • 実行速度は遅いので，純粋に数値計算のためだけにこのコードを使うことはおすすめしません．

前回まで

TensorFlowを(中途半端に)使って常微分方程式 (ODE)の数値計算をする
TensorFlowで力学系の解析(1) ヤコビアンの計算と平衡点の安定性解析
TensorFlowで力学系(2) 平衡点を探して安定性の解析

微分方程式をTensorflowのグラフ上で定義し、数値計算を行ったり、ヤコビ行列を求めたりしてきました。

Lyapunov 指数

自励系の常微分方程式

\begin{equation}
\frac{d \boldsymbol{x}}{dt} = f(\boldsymbol{x})
\tag{1}
\end{equation}

を考えます。 $\boldsymbol{x}$ は $d$ 次元ベクトルとします．
式(1)に従う解軌道 $\boldsymbol{x}(t)$ と，そのごく近傍にあって同じく(1)にしたがう解軌道 $\boldsymbol{x}'(t)$ を考え，
$\boldsymbol{x}'(t) = \boldsymbol{x}(t)+\delta(t)$ としてこの軌道の差 $\delta$ がどのように時間発展していくか？元の $\boldsymbol{x}(t)$ との差はどのように変化していくか？を考えます． $f$ のテイラー展開
$f(\boldsymbol{x}+\delta) = f(\boldsymbol{x}) +D_f(\boldsymbol{x}) \delta + o(|\delta|^2)$
から，$\delta$ が無限小のときの $\delta$ の時間発展は，次の線形化方程式

\begin{equation}
\frac{d \delta(t)}{dt} = D_f\left(\boldsymbol{x}(t)\right) \delta(t)
\tag{2}
\end{equation}

で表されます．ここで $D_f(x)$ はヤコビアンです．

２つの軌道は時間的に離れていくのか？という問いに応えるため，長期的に$\delta$ の大きさがどう変化するかに注目し，十分に大きな $t$ に対し

 | \delta(t) | \approx e^{\lambda t}| \delta(0) |

となるとき，この $\lambda$ を Lyapunov 指数と呼びます．
つまり

\begin{equation} \lambda = \lim_{t\rightarrow \infty}{ \frac{\log{| \delta(t) |}}{t}} \tag{3} \end{equation}

です． $\lambda$ が正の場合，２つの軌道は時間とともに指数的に離れていくことになります．これを軌道不安定性と呼びます．

数学的な詳細は参考文献1などを参照してください．

Lyapunov 指数の数値計算

$\delta(t)$ の解を数値的に求めるには，その発展方程式(2)はヤコビ行列の係数が $\boldsymbol{x}$ に依存して時間変化する変数係数の線形方程式ですので， $\boldsymbol{x}$ の時間発展を記述する(1)と(2)を同時に解く必要があります． $f$ がわかっている場合は，式(1)と式(2)をあわせて $2d$ 次元の微分方程式だと思い，ODEソルバーに渡して数値解を得ます．　また， $| \delta(t)|$ を長い時間計算することで大きくなりすぎたり小さくなりすぎて桁あふれ等が発生するのを防ぐため，一定期間ごとに $\delta(t)$ を正規化しなおし，そのときの倍率を記録しておきます． つまり一定期間ごとの時刻 $t_0, t_1, t_2,..., t_n, ...$ のときに $ \delta(t_n) \leftarrow \delta(t_n) /| \delta(t_n)|$ として$\delta$を更新し， このときの$a_n = | \delta(t_n)|$ を保存しておきます．そして

\lambda(t_n) = (1/t_n)\sum_{i=1}^{n}{\log{a_n}}

のように，各時刻で Lyapunov 指数の値を推定していきます．

TensorFlow とScipy による実装

今回もローレンツ方程式を扱います．

\begin{equation}
\frac{d \boldsymbol{x}}{dt} = f(\boldsymbol{x}) = 
\left( \begin{matrix}
f_x(\boldsymbol{x})  \\
f_y(\boldsymbol{x})  \\
f_z(\boldsymbol{x})
\end{matrix}\right) = 
\left( \begin{matrix}
\sigma(y-x)  \\
x(\rho -z) -y  \\
 xy - \beta z
\end{matrix}\right)  
\end{equation}

fやヤコビアンなどの定義

scipyのsolve_ivp関数をODEソルバーとして使います．

import sys
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import time

from scipy.integrate import solve_ivp

Lorenz方程式とヤコビアンのグラフを作る関数です． 前回までと同様なので説明省略します．

class Lorenz(object):
    def __init__(self, sigma=10., beta=8 / 3., rho=28., **kwargs):
        super().__init__(**kwargs)

        self.sigma = sigma
        self.beta = beta
        self.rho = rho

    def __call__(self, t, x):
        """ x here is [x, y, z] """
        # x = tf.cast(x, tf.float64)

        dx_dt = self.sigma * (x[1] - x[0])
        dy_dt = x[0] * (self.rho - x[2]) - x[1]
        dz_dt = x[0] * x[1] - self.beta * x[2]

        dX_dt = tf.stack([dx_dt, dy_dt, dz_dt])
        return dX_dt


def jacobian(t, f, x):
    """ return jacobian matrix of f at x"""
    n = x.shape[-1].value
    fx = f(t, x)
    if x.shape[-1].value != fx.shape[-1].value:
        print('For calculating Jacobian matrix',
              'dimensions of f(x) and x must be the same')
        return

    return tf.concat([tf.gradients(fx[i], x) for i in range(0, n)], 0)

fと線形化方程式を同時に計算するグラフ

元の常微分方程式とその軌道の周りに線形化した方程式 を同時に解くためのグラフを定義します． $f(\boldsymbol{x})$ と $D_f \delta$をそれぞれ求め，tf.concatを使って結合しています．


def f_with_df(x_and_d, f, dim=3):
  """
    combine f and its differentiation Df (tensor)
     args:
        x_and_d: tensor of x and d. 2*dim dimension
        f: rhs of the ode. 
        dim: dimension of x
  """
  x = x_and_d[0:dim]
  d = x_and_d[dim:2*dim]
  Df = jacobian(None, f, x)
  fx = f(None, x)
  Dfx_d = tf.linalg.matvec(Df, d)
  return tf.concat([fx, Dfx_d], 0)

数値計算用関数

上記で定義されたグラフを使って与えられた区間で $2d$ 次元の方程式を解く関数です．
ラッパー関数ではsession.runを呼び出して式(1)(2)の右辺の値を同時に計算します．

def solve_f_with_df(sess, fx_and_df_x_d, x0_and_d0, ts):
    """ numerically solve ode defined by f
        and its linearized equation dot_d =  Df_x d
    """
    # wrapper function
    def fdf_tf(t, xd):
      return sess.run(fx_and_df_x_d, feed_dict={x_and_d: xd})

    sol = solve_ivp(fun=fdf_tf,
                    t_span=[ts[0], ts[-1]], y0=x0_and_d0, t_eval=ts)
    return sol['y'], sol['t']

$\delta$ を正規化する関数です．

def normalize_vec(d):
    norm = np.sqrt(np.sum(np.square(d)))
    newd= d/norm
    return norm,newd

main関数部

初期値も3*2=6次元ベクトルで与えます．

dim = 3

# defining  parameters
rho = tf.Variable(28.0, dtype=tf.float64, name='rho')
sigma = tf.Variable(10.0, dtype=tf.float64, name='sigma')
beta = tf.Variable(8.0/3.0, dtype=tf.float64, name='sigma')

f_lorenz = Lorenz(sigma=sigma, rho=rho, beta=beta)

# state variable x and its perturbation delta
x_and_d = tf.placeholder(dtype=tf.float64, shape=(dim*2), name='x_and_d')
# rhs f(x) and  Df(x)* d
f_df_x = f_with_df(x_and_d, f_lorenz)

# initial value
x0_d0 = np.array([-3.73, -5.76, 20.14, 0.5, 0.2, 0.2])

総積分時間を2000, 正規化の間隔を10としています．

# integrating time
dt = 0.02
tstart = 0.0
tend =2000.0
ts = np.arange(tstart, tend+dt, dt)
len_t_sec = 10
nstep_t_sec = int( (len_t_sec/dt)+1)

t_sec = np.arange(tstart, tend, len_t_sec)

Session開始〜メインループ部分です．区間ごとに積分実行，xの軌道を保存，deltaの伸びを保存して正規化などを行なっています．

sess = tf.Session()
sess.run(tf.initializers.global_variables())

x_d = x0_d0.copy()  # intial condition
times = []
xs = []
norm_d_i = []

for i, t_i0 in enumerate(t_sec):
  ts_sec = t_i0 + dt* np.arange(0, nstep_t_sec)
  x_d_sec, _ = solve_f_with_df(sess, f_df_x, x_d, ts_sec)
  # record x and t
  times.extend(ts_sec[0:-1])
  xs.extend(x_d_sec[0:dim, 0:-1].transpose())  # record x
  # normalize d and record its stretch
  norm, newd = normalize_vec(x_d_sec[dim:2*dim, -1])
  norm_d_i.append(norm)
  # update x and d
  x_d[0:dim] = x_d_sec[0:dim, -1]
  x_d[dim:2*dim] = newd
sess.close()

結果の確認

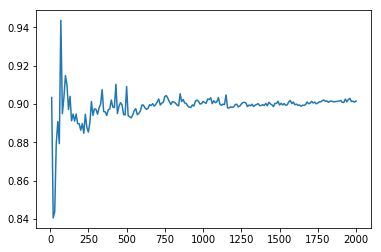
各区間での $\delta$ の伸び率のlogを取り，その後時間に対する平均を取ります． $\lambda$ の推定値が時間とともに揺らぎが少なくなり，
収束しているかをみるため，各区間ごとにそれまでの値を使って $\lambda$を計算し，横軸を時間にとったグラフを描きます．
このために，累積和をとるnp.cumsumを使っています．

# changing to numpy array
xs = np.array(xs)
times = np.array(times)
norm_d_i = np.array(norm_d_i)

lognorm_i = np.log(norm_d_i)
t_sec_l = t_sec + len_t_sec

lyap_t = np.cumsum(lognorm_i) / (t_sec_l)
plt.plot(t_sec_l, lyap_t)
plt.pause(0.001)
print('estimation of the largest Lyapunov exponent: {}'.format(lyap_t[-1]))

結果が下の図です．それなりに収束していることがわかります．

image.png

最終的な Lyapunov 指数の推定値は

estimation of the largest Lyapunov exponent: 0.9015374472045383

となったようです．計算時間を伸ばせば精度はより高まります．

code

githubにjupyter notebook を公開しています．
https://github.com/yymgch/ode_tf/blob/master/lyapunov_exponent.ipynb

次回

一部で話題の(?) Neural ODE っぽいことをやってみようかと思います．

TODO

  • 直交化などを実装してすべての Lyapunov spectrum を求める．
  • TensorFlow 2.0 への対応

  1. Eckmann, J. P., & Rueile, D. (1985). Ergodic theory of chaos and strange attractors. Reviews of Modern Physics, 57(3 Part I) 617-656
    $f$が適当な条件を満たせば，同じアトラクタに収束するような初期値の集合に関してはほとんどすべての 初期値 $(\boldsymbol{x}(0),\delta(0))$ に対して同じ$\lambda$ に収束することが知られています． ↩

7
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
7
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?