TensorFlowで力学系(2) 平衡点を探して安定性の解析

前々回、前回の続きとして，TensorFlowを使って力学系関係の数値解析をします．

今回は常微分方程式で表された力学系の平衡点がわからないときに、その位置を探します。
後半では分岐パラメータを変えながらに平衡点を追跡し、安定性解析を行って分岐点を見つけてみます．

今回はTensorFlowの自動微分に加え， TensorFlowの得意な最急降下法を使います．

ローレンツ系

例によってローレンツ方程式¹を使います．

\begin{equation}
\frac{d \boldsymbol{x}}{dt} = f(\boldsymbol{x}) = 
\left( \begin{matrix}
f_x(\boldsymbol{x})  \\
f_y(\boldsymbol{x})  \\
f_z(\boldsymbol{x})
\end{matrix}\right) = 
\left( \begin{matrix}
\sigma(y-x)  \\
x(\rho -z) -y  \\
 xy - \beta z
\end{matrix}\right)  
\end{equation}

で表されるベクトル場を考えます．

ローレンツ方程式の定義(importなどは省略）．

class Lorenz(object):
    def __init__(self, sigma=10., beta=8 / 3., rho=28., **kwargs):
        super().__init__(**kwargs)

        self.sigma = sigma
        self.beta = beta
        self.rho = rho

    def __call__(self, t, x):
        """ x here is [x, y, z] """
        # x = tf.cast(x, tf.float64)

        dx_dt = self.sigma * (x[1] - x[0])
        dy_dt = x[0] * (self.rho - x[2]) - x[1]
        dz_dt = x[0] * x[1] - self.beta * x[2]

        dX_dt = tf.stack([dx_dt, dy_dt, dz_dt])
        return dX_dt


def jacobian(t, f, x):
    """ return jacobian matrix of f at x"""
    n = x.shape[-1].value
    fx = f(t, x)
    if x.shape[-1].value != fx.shape[-1].value:
        print('For calculating Jacobian matrix',
              'dimensions of f(x) and x must be the same')
        return

    return tf.concat([tf.gradients(fx[i], x) for i in range(0, n)], 0)

ローレンツ方程式は原点の他に，アトラクタの持つ２つの回転している渦のような軌道それぞれの中心に平衡点をもっています．

この2つの平衡点は実は解析的に求めることができて，

\begin{equation} \left( \pm \sqrt{\beta (\rho-1)},\pm \sqrt{\beta (\rho-1)},\rho-1\right) \tag{1}
\end{equation}

と表せるのですが¹²，今回はそれを知らないと仮定して、TensorFlowを使って探してみましょう。

平衡点の探索

本来はNewton法を使って求めるのが収束が速い（2次の収束）のですが、今回はTensorFlow を使って手軽にできる最急降下法(Gradient Descent Method)を使い数値解を求めます。（Newton法をTensorFlowで実装することもできなくはないと思われますが今回はやりません）．

点 $\boldsymbol{x}^*$ が平衡点であるとは

 f(\boldsymbol{x}^*)=\boldsymbol{0} 

が成り立つことですので、$f$ のベクトルのノルム（大きさ） $|f|$ が小さいほど平衡点に近い、良い値だといえます．よってこのノルムの2乗を損失関数として定義します:

L(\boldsymbol{x}) = \left|f(\boldsymbol{x})\right|^2= f_x(\boldsymbol{x})^2 + f_y(\boldsymbol{x})^2 + f_z(\boldsymbol{x})^2. 

目的はこの損失関数が$0$となる点 $\boldsymbol{x}$ を求めることです． しかし $L \geq 0$なので，　$L$ を最小にする $\boldsymbol{x}$ を求めることと $L=0$ となる $\boldsymbol{x}$ を求めることが等価になります。

よって最急降下法による解候補 $\boldsymbol{x}_n$の逐次的な更新

\begin{equation}\boldsymbol{x}_{n+1} = \boldsymbol{x}_{n} - \gamma \frac{\partial L}{\partial \boldsymbol{x}}(\boldsymbol{x}_n) \tag{2} \end{equation}

を繰り返すことで、うまくすれば$L$ が最小値（０）となる点（に数値的に十分近い点) $\boldsymbol{x}$ を見つけることができるはずです．　ここで $\frac{\partial L}{\partial \boldsymbol{x}}(\boldsymbol{x}_n)$ は $L$ の$\boldsymbol{x}_n$ での勾配，$\gamma$ は学習率です．

ただし，注意すべきこととして，どの平衡点が見つかるかは初期値に依存します．
さらに局所最適解(local minima) に留まってしまう場合があります．　なので実践的には，解のあたりをつけて真の解に近そうな値を初期値ととる、多くの異なった初期値からの探索を繰り返す、などを行う必要があります³．

平衡点探索の実装

各変数やベクトル場の定義．

パラメータや $\boldsymbol{x}$ は学習や外部操作によって変えるものなので，今回はVariableとして定義します． x_initとinit_x_opは外からxに値を代入する手続きのためのplaceholderとオペレータです．

rho = tf.Variable(28.0, dtype=tf.float64, name='rho')
sigma = tf.Variable(10.0, dtype=tf.float64, name='sigma')
beta = tf.Variable(8.0/3.0, dtype=tf.float64, name='sigma')

f_lorenz = Lorenz(sigma=sigma, rho=rho, beta=beta)

# define a state variable x as Variable
x = tf.Variable([1,1,10], dtype=tf.float64, name='x') 
fx= f_lorenz(None,x)

# op for initialize x from outside of TF
x_init=  tf.placeholder(dtype=tf.float64, shape=(3), name='x_init')
init_x_op = tf.assign(x,x_init)

損失関数とオプティマイザーの設定

損失関数 $L$ をlossとして作り，オプティマイザーを指定して更新時に呼び出すオペレータを作ります． $\boldsymbol{x}$ の更新式(2)は手で実行せず，TensorFlowの一般的な学習手続きを使って行います．一般のニューラルネットワークでは重みwなどをオプティマイザーを使って学習により更新しましたが、今回は学習／更新の対象はxです。minimizeを指定するときに明示的に更新対象を指定しています。学習係数 $\gamma$ は $10^{-3}$ にとっています． この値は大きすぎると学習が発散します．

# square norm of f(x): sum_i{f_i(x)^2}
loss = tf.math.reduce_sum( tf.math.square(fx))

# optimizer
opt = tf.train.GradientDescentOptimizer(1e-3)
train_op = opt.minimize(loss, var_list=[x])

動作確認

xとloss の値を確認し，一回更新を走らせたあとで，値を最度確認し，更新が行われていることをチェックします．

sess =  tf.Session()
sess.run(tf.initializers.global_variables())

sess.run(init_x_op, feed_dict={x_init:[5,5,5]})
print("x:",sess.run(x))
print("loss:",sess.run(loss))

# update x by train op
print("update x by train op")
sess.run(train_op)
print("x:",sess.run(x))
print("loss:",sess.run(loss))

結果

x: [5. 5. 5.]
loss: 12236.111111111111
update x by train op
x: [-0.17666691  5.10333334  6.16222228]
loss: 3168.619885118489

という出力になり，たしかにxの値が変わってlossが下がっていることがわかりました．

探索を実行する関数

とりあえず関数で，探索するアルゴリズムを関数で実装してみます（あとでクラスを使ったものに書き換えます)．

探索を始める前に、xの値に初期値を代入する操作を先ほど作ったオペレータを使って行います。
式(2)の繰り返し適用による更新の実行も，一般的な学習手続きと似た形になります．
経過をみるために，10回ごとにxの値と損失（ノルムの大きさ）を出力しておきます。
終了条件は規定回数の更新が終わったか、または設定した誤差 eps 以内にノルムが収まったか、です。

def find_equilibrium(sess,loss,x0,step_max=10000,eps=1e-12,printinfo=True):
    # set initial candidate x
    sess.run(init_x_op, feed_dict={x_init:x0})
    print('initial state')
    print("x:", sess.run(x))
    step = 0
    np.set_printoptions(precision=5)  # 表示の精度設定

    lo =sess.run(loss)
    while(lo > eps and step < step_max):
        step += 1
        _, xval, lo = sess.run((train_op, x, loss))
        if printinfo and step % 10 == 0:
          print("step:{:d} x:{:} sqnorm(f):{:.5g}".format(step, xval, lo))
    print('final result')
    print("step:{:d} x:{:} sqnorm(f):{:.5g}".format(step,xval,lo))
    sucsess = lo < eps
    return xval, lo, sucsess

上で定義した関数を使って異なる初期値から探索を始め、３つの平衡点を見つけてみます．

x_eq1, sqnorm1, suc = find_equilibrium(sess,loss,[3,5,21])

x_eq2, sqnorm2, suc = find_equilibrium(sess,loss,[-4,-3,20])

x_eq0, sqnorm0, suc = find_equilibrium(sess,loss,[2,2,5])

実行結果

initial state
x: [ 3.  5. 21.]
step:10 x:[ 5.1554   6.10374 21.40182] sqnorm(f):1580.1
step:20 x:[ 6.54878  7.25577 23.35275] sqnorm(f):885.36
...(略)
step:150 x:[ 8.48528  8.48528 27.     ] sqnorm(f):1.436e-12
final result
step:152 x:[ 8.48528  8.48528 27.     ] sqnorm(f):8.2207e-13
（以下略）

最初の探索の結果の一部だけを載せています． 152回で探索が終わり、平衡点に十分近い値 $（8.48528, 8.48528, 27）$ がみつかりました。このパラメータでの真の平衡点(1)とよい精度で一致しています。

他の２点の初期値からの実行結果は省略しますが，実行してみると，違う平衡点に収束していることがわかります．

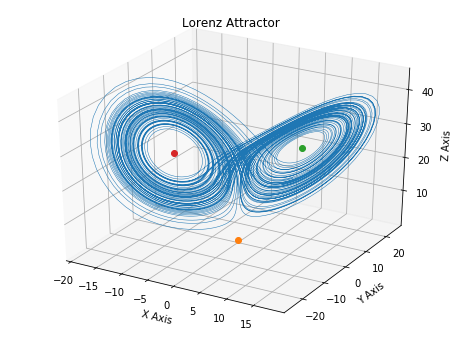
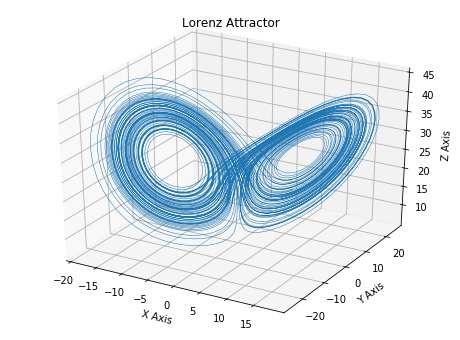
アトラクタの軌道と，３点の平衡点を描いた図は以下のようになります．

予想通り渦の中心に平衡点が存在しています．

パラメータの変化に伴う平衡点の変化の追跡と分岐点の探索

パラメータ，たとえば $\rho$ などのを変えると，平衡点の位置も変わります．
パラメータを一定の範囲で変えていったときに動いていく平衡点を追跡してみます．そして，パラメータの変化とともに平衡点の安定性がどう変わるか，観察してみます．

平衡点がなくなる，２つに別れるなどの分岐が起きた場合どう追跡するかはテクニカルな点が多いのでここでは扱いません． 著名な分岐解析ツールには AUTOなどがあります．

探索アルゴリズムのクラス

上で行った「微分方程式と初期値を与えて平衡点を探す手続き」をクラスを使って定義しておきます．こうしておくことで，損失関数やオプティマイザを隠蔽化しておくことができます．
クラスの__init__時にパラメータやグラフを作成し，findが呼び出されると平衡点探索を実行します．ステップ数や精度などの結果の詳細はメンバ変数に格納します．その他のことは上と同じです．

class Find_equilibrium:
    def __init__(self, f, eps=1e-12, infolevel=2):
        self.eps = eps # precision
        self.infolevel = infolevel
        self.x = tf.Variable([1,1,10], dtype=tf.float64, name='x') # candidate of equilibrium
        self.fx= f(None,self.x)
        # squarenorm of f(x): sum_i{f_i(x)^2}
        self.loss = tf.math.reduce_sum( tf.math.square(self.fx))

        # op for initialize x from outside of TF
        self.x_init=  tf.placeholder(dtype=tf.float64, shape=(3), name='x_init')
        self.init_x_op = tf.assign(self.x,self.x_init)

        # optimizer

        opt = tf.train.GradientDescentOptimizer(1e-3)
        self.train_op = opt.minimize(self.loss, var_list=[self.x])

    def find(self, sess, x0, step_max=10000):
        sess.run(self.init_x_op, feed_dict={self.x_init: x0})
        if self.infolevel >= 1:
            print('initial state')
            print("x:", sess.run(self.x))
        step = 0
        np.set_printoptions(precision=5)

        lo =sess.run(self.loss)
        # gradient descent search
        while(lo > self.eps and step < step_max):
            step += 1
            _, xval, lo = sess.run((self.train_op, self.x, self.loss))
            if self.infolevel>=2 and step % 10 == 0:
                print("step:{:d} x:{:} sqnorm(f):{:.5g}".format(step, xval, lo))
        # show final results
        if self.infolevel >= 1:
            print('final result')
            print("step:{:d} x:{:} sqnorm(f):{:.5g}".format(step,xval,lo))

        # record results to member variable
        self.sucsess = lo < self.eps
        self.xeq = xval
        self.sqnorm = lo
        self.step = step
        return xval

分岐パラメータ探索

これを使って， $\rho$ を2.0から30.0まで変えて平衡点を追ってみます．そして各平衡点で，ヤコビアンとその固有値を計算し，安定性を調べ，安定性が変わるところを探してみます．ヤコビアンとは何か？に関しては前回を参照してください．

今回探す平衡点は渦の中心のひとつにあたるものです．

グラフの作成

　feqが探索アルゴリズムのクラスです．

tf.reset_default_graph()

rho = tf.Variable(28.0, dtype=tf.float64, name='rho')
sigma = tf.Variable(10.0, dtype=tf.float64, name='sigma')
beta = tf.Variable(8.0/3.0, dtype=tf.float64, name='sigma')
# rho を変えるop
rho_as = tf.placeholder(shape=(),dtype=tf.float64)
assign_rho_op = tf.assign(rho,rho_as)

f_lorenz = Lorenz(sigma=sigma, rho=rho, beta=beta)
feq = Find_equilibrium(f_lorenz, eps=1e-12, infolevel=1)
Df = jacobian(None,f_lorenz,feq.x)

初期値，パラメータの範囲など設定

#initial guess
x0 = np.array([3.0,3.0,10])
# range of bifurcation parameter rho
rho_max = 30
rho_min = 2.0
rho_step = 0.5
rs = np.arange(rho_min, rho_max+rho_step,rho_step)

パラメータを変えながら平衡点を探索． 平衡点が見つかったらヤコビアンの固有値を計算

探索が終わった後に，平衡点の値を次の探索の初期値としています．パラメータの変化に対して連続に平衡点が動くことが多いので，これにより同じ平衡点を追い続けることができやすくなります．

sess=tf.Session()
sess.run(tf.initializers.global_variables())

xeqs=[]
eigvals = []

for r in rs:
    sess.run(assign_rho_op, feed_dict={rho_as:r})  # assign rho value
    xeq = feq.find(sess,x0,step_max=10000)
    xeqs.append(xeq)

    # jacobian and eigenvalues of equiribrium
    df = sess.run(Df)
    eigval, eigvecs = np.linalg.eig(df)
    eigvals.append(eigval)
    x0 = xeq # set next starting point
sess=tf.Session()
sess.run(tf.initializers.global_variables())
​
xeqs=[]
eigvals = []
​
for r in rs:
    sess.run(assign_rho_op, feed_dict={rho_as:r})  # assign rho value
    xeq = feq.find(sess,x0,step_max=10000)
    xeqs.append(xeq)
​
    # jacobian and eigenvalues of equiribrium
    df = sess.run(Df)
    eigval, eigvecs = np.linalg.eig(df)
    eigvals.append(eigval)
    x0 = xeq # set next starting point

結果の図示

(コードは省略）

平衡点の変化をみてみます．

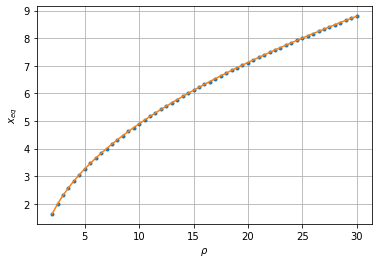
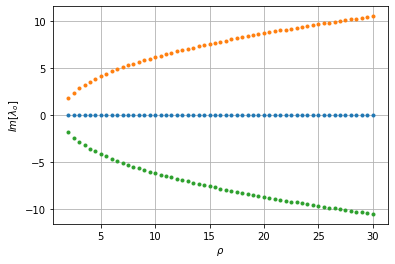
青い点が横軸の各 $\rho$ で計算された平衡点の $x$ の値です． オレンジは式(1)を直接計算した真の値です．よく一致していることがわかります．

こちらは，各固有値の実部です．

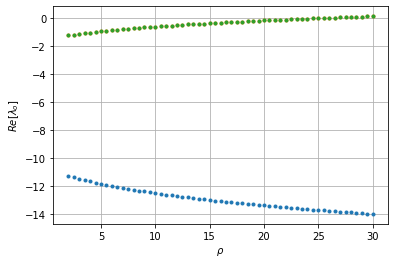
　$\rho$ が25になる手前くらいでふたつの固有値の実部が０を横切って正になっています．（図では緑の点しか見えませんが，実部の同じ二つの同じ固有値がふたつ重なっています）．ここで分岐が起きてこの平衡点が不安定化しているようです．

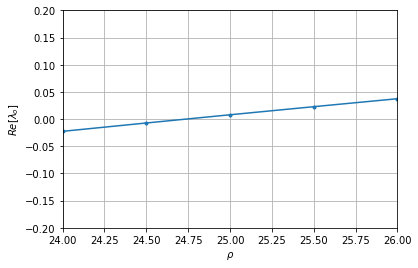
この部分を拡大したものが次の図です．

目で補完すると横切っているのは24.75の手前ようです．解析的にはこの分岐点は

\rho = \frac{\sigma (\sigma + \beta +3)}{\sigma -\beta -1} \approx 24.73684

なので¹²，ほぼ一致しているようです⁴．

下図は固有値の虚部の変化です．渦の中心であることから予想されるように，複素固有値を持っています．この図だけではわかりにくいですが，実部が0を横切っているのは，この複素数になっている固有値ですので，この分岐はHopf分岐であることがわかります．

#まとめ
無事平衡点を探して安定性解析を行う，という力学系の基本的な解析がTensorFlow上でできました．
実際は局所解に落ちていないかのチェックなどが必要です．

次回

TensorFlowを使って最大リアプノフ指数を数値計算します．

TODO

• rho変えていくループ中で，平衡点が見つからなかった場合の処理など

code

githubにJupyter Notebookを公開しています．
https://github.com/yymgch/ode_tf/blob/master/finding_equiribrium.ipynb

1. Lorenz, Edward N. "Deterministic nonperiodic flow." Journal of the atmospheric sciences 20.2 (1963): 130-141.
   前回同様$\boldsymbol{x}$を３次元のベクトル，成分は$(x,y,z)$として ↩ ↩² ↩³

2. Lorenz Attractor, Wolfram Mathworld ↩ ↩²

3. $\gamma$ が十分小さいとき，これを時間ステップ幅とみると式(2)は勾配系の微分方程式のEuler近似になっており，もとの勾配系では$L$ がリヤプノフ関数となっているため，1回の更新毎に$L$は更新前以下の値になると考えられます． ですが一般的な状況では平衡点以外にも(2)において$\frac{\partial L}{\partial \boldsymbol{x}}=0$となる局所最適解は存在する可能性があるため，平衡点にたどり着くかどうかは初期値しだいです． ↩

4. 分岐点を最急降下法で見つけることをTensorFlowで実装できるか？　今回はやらなかったですが，AUTOのアルゴリズムに詳しい人とかならできるかもしれません． ↩