TensorFlowを(中途半端に)使って常微分方程式 (ODE)の数値計算をする

TensorFlowを使って常微分方程式(ODE)の初期値問題の数値計算をやってみます。速度の面では実用性はありませんが、TensorFlowに備わっている強力な自動微分を使いこなせれば色々解析に便利な面があると思われ、たとえばNeural Networkなどで複雑なモデルを作っていたとしてもヤコビ行列の計算などを自動的にしてくれることなどが利点と思います。

今回はグラフを使って微分方程式を定義してみますが、実際の数値計算はscipyに入っているsolve_ivpを使用します。 実は拡張ライブラリのTensorFlow Probability においてTensorFlow上で動くODEソルバーが実装されているようですが、理解不足もあり今回は使いません。

環境

• TensorFlow 1.14
• Python 3.6.8
• scipy 1.2.1

やりたいこと

一階の常微分方程式

\frac{d \boldsymbol{x}}{dt} = f(\boldsymbol{x})

の初期値問題の近似解を数値計算により求めます。 $\boldsymbol{x} \in \mathbb{R}^{d}$は$d$次元ベクトル、$f$は$\mathbb{R}^{d}$ から $\mathbb{R}^{d}$への写像（ベクトル場と呼ぶ）とします。

例として次のローレンツ方程式を以後使います。３次元の微分方程式であり、E.ローレンツがカオスを発見したことで有名です。 $\boldsymbol{x}=(x,y,z)^T$ として

\begin{equation}
\frac{d \boldsymbol{x}}{dt} = 
\left( \begin{matrix}
f_x(\boldsymbol{x})  \\
f_y(\boldsymbol{x})  \\
f_z(\boldsymbol{x})
\end{matrix}\right) = 
\left( \begin{matrix}
\sigma(y-x)  \\
x(\rho -z) -y  \\
 xy - \beta z
\end{matrix}\right)  \tag{1}
\end{equation}

$\sigma, \rho, \beta $ は定数のパラメータです。

この方程式をTensorFlowのグラフ上で定義し、ODEソルバーを使って数値解を求めてみたいと思います。尚，今回は倍精度で計算を行います．

#グラフの定義

##準備
tensorflow, scipyのodeソルバー呼び出しに使うsolve_ivp，その他をインポートします．

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D  # noqa: F401 unused import
import time 

import tensorflow as tf
from scipy.integrate import solve_ivp

##ベクトル場の定義

まず変数 $\boldsymbol{x}$ のテンソルですが外(ODEソルバー）から値を入れて使うので、今回はこんな感じでplaceholder型にします。

x = tf.placeholder(dtype=tf.float64, shape=(3), name='x')

入力$x$からベクトル場を計算するグラフを作るクラスを作ります。インスタンスを作っておき，パラメータはメンバ変数に持たせるようにしておくと便利です。（参考: https://github.com/titu1994/tfdiffeq/blob/master/examples/lorenz_attractor.py )

class Lorenz(object):

    def __init__(self, sigma=10., beta=8 / 3., rho=28., **kwargs):
        self.sigma = float(sigma)
        self.beta = float(beta)
        self.rho = float(rho)

    def __call__(self, t, x):
        dx_dt = self.sigma * (x[1] - x[0])
        dy_dt = x[0] * (self.rho - x[2]) - x[1]
        dz_dt = x[0] * x[1] - self.beta * x[2]

        dX_dt = tf.stack([dx_dt, dy_dt, dz_dt])
        return dX_dt

グラフの作成

f_lorenz = Lorenz()
fx = f_lorenz(None, x)  # r.h.s. of ODE

Sessionを動かして計算

とりあえず初期値を設定しておきます．

x0 = np.array([1, 10, 10], dtype=np.float64)   # initial value

sessionの開始，動作の確認

sess = tf.Session()
sess.run(tf.initializers.global_variables())

$\boldsymbol{x}$に初期値$(1,10,10)$を入れたときに$f(\boldsymbol{x})$を正しく計算してるか見てみます．

print('###value of f(x)###')
print(sess.run(fx, feed_dict={x:x0})) 

結果

###value of f(x)###
[ 90.           8.         -16.66666667]

手計算だと$(90,8,-50/3)$ですので，ちゃんと計算していることがわかります．

ODEソルバーによる数値計算

では準備ができたので，これをODEソルバーに渡して数値解を計算してみます．
scipyのsolve_ivp のドキュメントはここです．デフォルトでは(適応的時間刻み制御付）4次のルンゲ=クッタ法が実際に使われるようです．

時間の設定

積分の開始，終了時刻を設定しておきます．今回きれいに図を描くため時間刻み0.01ごとの値を得たいため，配列tsを作っておきます．

dt=0.01
tstart=0.0
tend=100.0
ts=np.arange(tstart, tend+dt, dt)  # 表示のため、0.01ステップで値を出力させる

ODEソルバーに渡すラッパー関数の作成

solve_ode に渡す関数の形式にするためのラッパー関数です．引数のxtをplaceholderに渡し，fxを評価するrunを走らせるだけです． lambdaを使えばより簡潔にすることもできます．

def f_lorenz_tf(t,xt):
    return sess.run(fx, feed_dict={x: xt})

ソルバーによる数値解の計算

ソルバーsolve_ivpに上で作ったベクトル場を計算する関数，初期値x0,積分の開始，終了時刻，値を出力する時間のリスト，を渡して数値計算を行わせ，結果などをsol_lorenzに受け取ります．返り値のなかの['t']に時間ステップ，['y']に解が入っているので，それぞれを取り出します．

start_time =time.time() # measurement of time
sol_lorenz = solve_ivp(fun=f_lorenz_tf,
                       t_span=[tstart, tend], y0=x0, t_eval=ts)
integration_time_tf = time.time() - start_time
t_lo = sol_lorenz['t']   # 各ステップの時刻を取得
x_lo = sol_lorenz['y']  # 各ステップのx(t)の値を取得

print("processing time (tf) %.5f" % integration_time_tf)

結果の表示

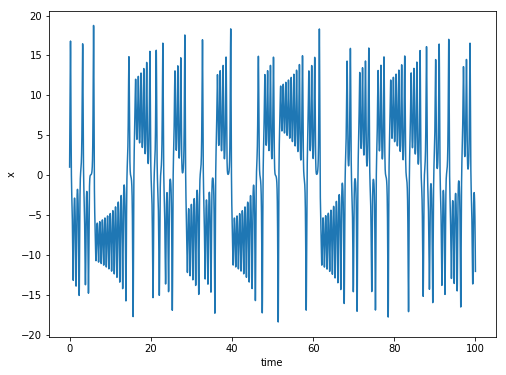
解曲線を表示してみます．

fig=plt.figure(figsize=(8,6))
ax=fig.add_subplot(111)

ax.plot(t_lo,x_lo[0],'-')
ax.set_xlabel('time')
ax.set_ylabel('x')
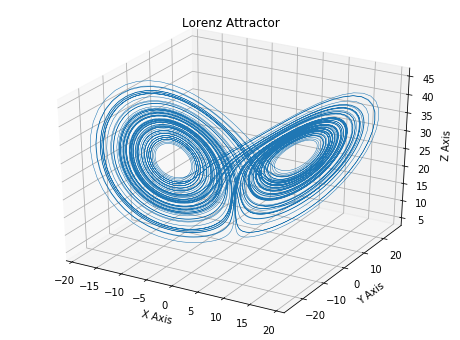
# 3dim phase space
fig3 = plt.figure(figsize=(8,6))
ax3 = fig3.add_subplot(111,projection='3d')

ax3.plot(x_lo[0], x_lo[1], x_lo[2], '-', lw=0.5)
ax3.set_xlabel("X Axis")
ax3.set_ylabel("Y Axis")
ax3.set_zlabel("Z Axis")
ax3.set_title("Lorenz Attractor")

numpyとの比較

numpyのみを使って微分方程式を計算した場合と比較してみます。
まずtensorflowを使わずにローレンツ方程式のfを定義します。扱っているものはnumpy配列かtensorかで違うのですが，コード上では最後のreturn文以外は同じ処理になります。

class Lorenz_np(object):

    def __init__(self, sigma=10., beta=8 / 3., rho=28., **kwargs):
        self.sigma = float(sigma)
        self.beta = float(beta)
        self.rho = float(rho)

    def __call__(self, t, x):
        """ x here is [x, y, z] """
        dxdt=  self.sigma * ( x[1] - x[0])
        dydt= x[0] * (self.rho- x[2] ) - x[1]
        dzdt= x[0]*x[1]-self.beta*x[2]
        return np.array([dxdt,dydt,dzdt   ])

そしてこの関数をodeソルバーに渡して計算します．

f_lorenz_np = Lorenz_np()
start_time = time.time()  # measurement of time
sol_lorenz_np = solve_ivp(fun=f_lorenz_np,
                          t_span=[tstart, tend], y0=x0, t_eval=ts)
integration_time_np= time.time() - start_time
print("processing time (numpy) %.5f" % integration_time_np)

t_lo_np = sol_lorenz_np['t']
x_lo_np = sol_lorenz_np['y']

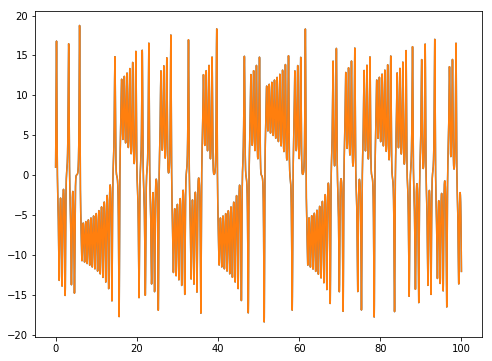
解軌道を比較してみます．

fig3=plt.figure(figsize=(8,6))
ax3=fig3.add_subplot(111)

ax3.plot(t_lo,x_lo[0],'-')
ax3.plot(t_lo_np,x_lo_np[0],'-')

２つの解曲線がまったく同一なので，重なってひとつにみえています．どうやら内部的には完全に同じ計算を
しているようですね．　この方程式にはカオスの初期値鋭敏姓があるので，数学的には同一の式でも，計算の手順や精度を少しでも変えるだけでも数値計算の結果は変わってしまいます．たとえば
たとえばLorenz_npの__call___の１行目を

   dxdt=  sigma *  x[1] - sigma*x[0]

と少し変えるだけで，丸め誤差は発生し，その誤差が時間とともに指数的に拡大するため，数値計算の結果は目に見えて変わります．

速度について

コードの中には積分にかかった時間を計算していました．手元のマシンでは

processing time (TF): 2.97551
processing time (numpy) 0.22292

という結果になりました． 3秒とは...遅いですね。numpyと比べてもTensorFlowのほうが10倍遅いです。sess.run をsolve_ivpの中で10000回近く呼んでいることのオーバーヘッドでしょうか。まあnumpyもC++などに比べると100倍くらい遅いのではないかと思いますが．
尚これはCPUのみでの結果ですが、GPUを使うとさらに遅くなります。

#終わりに

ひとまずTensorFlowを使ってベクトル場を計算することで微分方程式の計算が可能であるということは確かめられました．

次回

今回の範囲ではTensorFlowを使う意義がまったくない感じられないと思いですので，次回は勾配を計算する機能を使ってヤコビ行列を計算することにより、不動点の安定性解析やリアプノフ指数の計算といった力学系の解析をやってみたいと思います．

TODO

• バッチ処理に対応できるようにする。
• Tensorflow上でODEsolverを動かす。

code

githubにjupyterNotebookを公開しました．
https://github.com/yymgch/ode_tf/blob/master/ode_by_tf.ipynb