TL;DR:
- Pythonでbacktestする際のTipsをまとめたものです.
- 面倒な前処理をさくっと終わらせてモデル作りに専念したい方向けに実用的なコードサンプルを載せています。
- 記事では紹介していませんが,
pandas-datareaderで基本的なマクロデータは取得可能であるため,複数因子モデルなど,さまざまなポートフォリオ選択モデルを試すことができます.
Overview:
- PythonでBacktestする環境を整える.
- 東証TOPIX構成銘柄から対象資産を選び最小分散ポートフォリオを組む.
1. データ
株価データの取得
まず,pandas-datareaderを環境にインストールします.
pandas-datareaderは,株価などの市場データをWeb API経由でダウンロードできる(pandas.Dataframe friendlyで)便利なPythonパッケージです.IEX, World Bank, OECD, Yahoo! Finance,FRED,StooqなどのAPIを内部で叩き、pythonコード上に取得したデータを読み込みことができます.詳しい使い方は公式ドキュメントを参照してください.
# Install pandas-datareader (latest version)
$ pip install git+https://github.com/pydata/pandas-datareader.git
# Or install pandas-datareader (stable version)
$ pip install pandas-datareader
今回は,東京証券取引所(東証)に上場している株式銘柄を対象商品とします.
Web上で公開されているデータは圧倒的に米国市場のものが多いですが,ポーランドの最強サイトstooq.comは東京証券取引所の過去データを公開しています.pandas-datareaderを使ってstooqから個別銘柄のデータを取得しましょう.
基本的には,pandas_datareader.stooq.StooqDailyReader()を実行すればOKです.引数には,各市場に登録してある証券コード(or ティッカーシンボル)と、データ公開元のサイト(Yahoo!, Stooq, ...)を指定します.
東京証券取引所で取り扱いされている株式銘柄には,4桁の証券コードが割り当てられているので、今回はこれを使います.(例:トヨタ自動車の株式は、東証では証券コードが7203である銘柄として,NYSEではティッカーシンボルがTMである銘柄として取引されています.)
試しに,トヨタ自動車(東証:7203)の株価データを取得してプロットしてみましょう,
import datetime
import pandas_datareader
start = datetime.datetime(2015, 1, 1)
end = datetime.datetime(2020, 11, 30)
stockcode = "7203.jp" # Toyota Motor Corporation (TM)
df = pandas_datareader.stooq.StooqDailyReader(stockcode, start, end).read()
df = df.sort_values(by='Date',ascending=True)
display(df) # show df
Open High Low Close Volume
Date
2015-01-05 6756.50 6765.42 6623.43 6704.69 10653925
2015-01-06 6539.48 6601.09 6519.83 6519.83 13870266
2015-01-07 6480.52 6685.05 6479.64 6615.40 12837377
2015-01-08 6698.46 6748.46 6693.98 6746.69 11257646
2015-01-09 6814.56 6846.70 6752.92 6795.80 11672928
... ... ... ... ... ...
2020-11-04 7024.00 7054.00 6976.00 6976.00 6278100
2020-11-05 6955.00 7032.00 6923.00 6984.00 5643400
2020-11-06 7070.00 7152.00 7015.00 7019.00 11092900
2020-11-09 7159.00 7242.00 7119.00 7173.00 7838600
2020-11-10 7320.00 7360.00 7212.00 7267.00 8825700
日別の株価推移データがpandas.Dataframeとして取得できました!
いま作成したdfの中身をプロットしてみます.(基本的に終値をつかいます)
# Plot timeseries (2015/1/1 - 2020/11/30)
plt.figure(figsize=(12,8))
plt.plot(df.index, df["Close"].values)
plt.show()
下図のように,終値(Close)の推移が簡単にプロットできました.

対象資産のパネルデータを作る
ポートフォリオ最適化問題を解くための準備として,複数の資産(株式銘柄)に対するパネルデータを作り,pandas.Dataframeオブジェクトとして整理します.
今回はTOPIX 500に掲載されている銘柄から5つ選び,投資対象資産とします.また,前処理として「終値」を「終値ベースの収益率」へ変換しています.この部分のコードは状況に合わせて変えてください.
import datetime
import numpy as np
import pandas as pd
import pandas_datareader.data as web
import pandas_datareader.stooq as stooq
def get_stockvalues_tokyo(stockcode, start, end, use_ratio=False):
"""
stockcode: market code of each target stock (ex. "NNNN") defined by the Tokyo stock market.
start, end: datetime object
"""
# Get index data from https://stooq.com/
df = stooq.StooqDailyReader(f"{stockcode}.jp", start, end).read()
df = df.sort_values(by='Date',ascending=True)
if use_ratio:
df = df.apply(lambda x: (x - x[0]) / x[0] )
return df
def get_paneldata_tokyo(stockcodes, start, end, use_ratio=False):
# Use "Close" value only
dfs = []
for sc in stockcodes:
df = get_stockvalues_tokyo(sc, start, end, use_ratio)[['Close']]
df = df.rename(columns={'Close': sc})
dfs.append(df)
df_concat = pd.concat(dfs, axis=1)
return df_concat
get_paneldata_tokyo()を使ってパネルデータを作成します.
start = datetime.datetime(2015, 1, 1)
end = datetime.datetime(2020, 11, 30)
stockcodes=["1301", "1762", "1820", "1967", "2127"]
df = get_paneldata_tokyo(stockcodes, start, end, use_ratio=True)
display(df) # return ratio daily
1301 1762 1820 1967 2127
Date
2015-01-05 0.000000 0.000000 0.000000 0.000000 0.000000
2015-01-06 -0.010929 -0.018385 -0.033937 -0.002265 -0.038448
2015-01-07 -0.014564 -0.020433 -0.059863 -0.013823 -0.059680
2015-01-08 -0.007302 -0.016338 -0.057883 -0.013823 -0.039787
2015-01-09 0.000000 -0.004490 -0.031938 -0.025407 -0.043770
... ... ... ... ... ...
2020-10-29 0.096138 -0.032923 -0.030777 0.858573 5.682321
2020-10-30 0.093336 -0.039657 -0.041199 0.832831 5.704266
2020-11-02 0.107748 -0.026188 -0.032198 0.845702 5.418978
2020-11-04 0.099341 -0.024392 -0.020829 0.858573 5.704266
2020-11-05 0.069315 -0.014964 -0.042147 0.904909 6.055390
これで,評価対象となる各資産のパネルデータを取得できました.
2. 理論
投資対象となる複数の資産に対して,適当な投資比率をそれぞれ決定することをポートフォリオ最適化といいます.今回は,最も基本的なポートフォリオ最適化の問題設定として,Markowitzが提唱した平均分散モデル(Mean-Variance Model)を採用します.
Markowitzの平均分散モデル
Markowitzの平均分散モデルでは,「ポートフォリオの期待収益率(Expected return)が一定値以上となる」という制約条件の下で,「ポートフォリオの分散を最小化する」最適化問題を考えます.
一般に,$n$コの資産で構成されるポートフォリオの場合,ポートフォリオの分散は$n$コの資産間の共分散行列の二次形式となるので,この最適化問題は二次計画問題(Quadratic Programming, QP)のクラスとなり,次のように定式化されます.
$$
\begin{align}
\underset{\bf x}{\rm minimize} ~~~ &{\bf x}^T \Sigma {\bf x} \\
{\rm subject~to} ~~~ &{\bf r}^T {\bf x} = \sum_{i=1}^{n} r_i x_i \geq r_e \\
&{|| {\bf x} ||}_{1} = \sum_{i=1}^{n} x_i = 1 \\
&x_i \geq 0 ~~ (i = 1, \cdots, n)
\end{align}
$$
- $\Sigma \in \mathbb{R}^{n \times n}$ ー $n$コの資産の共分散行列
- ${\bf x} \in \mathbb{R}^{n}$ ー $n$コの資産の投資比率ベクトル
- $\bar{\bf r} \in \mathbb{R}^{n}$ ー $n$コの資産の期待収益率ベクトル
- $x_i \in \mathbb{R}$ ー 資産$i$の投資比率
- $\bar{r}_i \in \mathbb{R}$ ー 資産$i$の期待収益率
- $r_e \in \mathbb{R}$ ー 投資家の要求期待収益率
- $\bar{r}_p \in \mathbb{R}$ ー ポートフォリオの収益率の期待値
- $\sigma_p \in \mathbb{R}$ ー ポートフォリオの収益率の標準偏差
1つ目の制約式は,ポートフォリオの期待収益率が一定値($=r_e$)以上となることを要請しています.2つ目,3つ目の制約式はポートフォリオの定義からくる自明なものです.資産の空売りを許す場合,3つ目の制約式を除くこともあります.
CVXOPTの使い方
Pythonの凸最適化向けパッケージCVXOPTを使って,この二次計画問題(QP)を解きます.
CVXOPTで二次計画問題を扱う場合は,解きたい最適化問題を以下の一般化されたフォーマットに整理して,
$$
\begin{align}
\underset{\bf x}{\rm minimize} ~~~ &\frac{1}{2} {\bf x}^{T} P {\bf x} + {\bf q}^{T} {\bf x} \\
{\rm subject~to} ~~~ & G {\bf x} \leq {\bf h} \\
&A {\bf x} = {\bf b}
\end{align}
$$
パラメータP,q,G,h,Aを計算し,cvxopt.solvers.qp()関数を実行することで最適解と最適値を求めます.Markowitzの平均・分散モデルの場合は,
$$
P = 2 \cdot \Sigma, ~~~
q = {\bf 0}_n, ~~~
G = -1 \cdot
\begin{pmatrix}
\bar{r}_1 & \cdots & \bar{r}_n \
1 & \cdots & 0 \\
\vdots & \ddots & \vdots \\
0 & \cdots & 1
\end{pmatrix}, ~~~
h = -1 \cdot
\left(
\begin{array}{c}
r_e \\
0 \\
\vdots \\
0
\end{array}
\right), ~~~
A = {\bf 1}_n^{\mathrm{T}}, ~~~
b = 1
$$
となります.
参考:
- https://cvxopt.org/userguide/coneprog.html#quadratic-programming
- https://qiita.com/ryoshi81/items/8b0c6add3e367f94c828
Pythonによる求解
対象資産のパネルデータdfから,最適値を求めるために必要な統計量を計算します.
ポートフォリオ内の資産間の共分散行列 $\Sigma$:
df.cov() # Covariance matrix
1301 1762 1820 1967 2127
1301 0.024211 0.015340 0.018243 0.037772 0.081221
1762 0.015340 0.014867 0.015562 0.023735 0.038868
1820 0.018243 0.015562 0.025023 0.029918 0.040811
1967 0.037772 0.023735 0.029918 0.109754 0.312827
2127 0.081221 0.038868 0.040811 0.312827 1.703412
ポートフォリオ内の各資産の期待収益率 ${\bf r}$:
df.mean().values # Expected returns
array([0.12547322, 0.10879767, 0.07469455, 0.44782516, 1.75209493])
CVXOPTを使って最適化問題を解く.
import cvxopt
def cvxopt_qp_solver(r, r_e, cov):
# CVXOPT QP Solver for Markowitz' Mean-Variance Model
# See https://cvxopt.org/userguide/coneprog.html#quadratic-programming
# See https://cdn.hackaday.io/files/277521187341568/art-mpt.pdf
n = len(r)
r = cvxopt.matrix(r)
P = cvxopt.matrix(2.0 * np.array(cov))
q = cvxopt.matrix(np.zeros((n, 1)))
G = cvxopt.matrix(np.concatenate((-np.transpose(r), -np.identity(n)), 0))
h = cvxopt.matrix(np.concatenate((-np.ones((1,1)) * r_e, np.zeros((n,1))), 0))
A = cvxopt.matrix(1.0, (1, n))
b = cvxopt.matrix(1.0)
sol = cvxopt.solvers.qp(P, q, G, h, A, b)
return sol
r = df.mean().values # Expected returns
r_e = 0.005 * # Lower bound for portfolio's return
cov = df.cov() # Covariance matrix
# Solve QP and derive optimal portfolio
sol = cvxopt_qp_solver(r, r_e, cov)
x_opt = np.array(sol['x'])
print(x_opt)
print("Variance (x_opt) :", sol["primal objective"])
pcost dcost gap pres dres
0: 4.3680e-03 -8.6883e-02 5e+00 2e+00 2e+00
1: 9.1180e-02 -2.2275e-01 5e-01 1e-01 1e-01
2: 2.1337e-02 -6.0274e-02 8e-02 2e-16 1e-16
3: 1.0483e-02 -1.7810e-03 1e-02 1e-16 3e-17
4: 4.9857e-03 1.5180e-03 3e-03 2e-16 8e-18
5: 4.0217e-03 3.6059e-03 4e-04 3e-17 1e-17
6: 3.7560e-03 3.7107e-03 5e-05 3e-17 1e-18
7: 3.7187e-03 3.7168e-03 2e-06 1e-17 4e-18
8: 3.7169e-03 3.7168e-03 2e-08 1e-16 6e-18
Optimal solution found.
[ 5.56e-05]
[ 1.00e+00]
[ 1.76e-05]
[ 3.84e-07]
[ 2.63e-07]
Variance (x_opt): 0.003716866155475511 # 最適ポートフォリオの分散
最適解(各資産への最適な投資比率)と,最適値(最適な投資比率を適用した場合のポートフォリオの分散)が求められました.なお,今回使った平均分散モデルによる最適解はポートフォリオのリスク(分散)に対する最適性を重視しているので,「最小分散ポートフォリオ」と呼ばれます.
なお,収益率に対する評価指標には,無リスク資産の収益率(インフレ率)を加味したシャープレシオを用いるケースが多いです.backtestの方法についてはいくつか流儀があるので,専門書や論文を参照してください.
3. 実装
上のコードをまとめて,自作のバックテスト用PythonクラスMarkowitzMinVarianceModel()を作りました.実装の参考例としてスクリプトを紹介します.
バックテスト用のPythonクラス
import cvxopt
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
class MarkowitzMinVarianceModel():
"""
Args:
=====
- df: pandas.dataframe
panel data for target assets for the portfolio.
its index must be `numpy.datetime64` type.
its columns must be time-series data of target assets.
- window_size: int
the size of time-window which is used when deriving (or updating) the portfolio.
- rebalance_freq: int
rebalance frequency of the portfolio.
- r_e: float
min of the return ratio (= capital gain / investment).
- r_f: float
rate of returns of the risk-free asset.
"""
def __init__(self, df, window_size, rebalance_freq, r_e=None, r_f=None):
self.df = self._reset_index(df)
self.df_chg = self.df.pct_change()
self.df_chg[:1] = 0.0 # set 0.0 to the first record
self.df_bt = None
self.df_bt_r = None
self.df_bt_x = None
self.window_size = window_size
self.rebalance_freq = rebalance_freq
self.jgb_int = 0.0001 # 0.01% per year (Japanese Government Bond)
self.r_f = r_f if r_f is not None else self.jgb_int * (1/12) # adjust monthly
self.r_e = r_e if r_e is not None else r_f
def _reset_index(self, df):
df = df.copy()
df['date'] = pd.to_datetime(df.index)
df = df.set_index('date')
return df
def get_dfbt_r(self):
return self.df_bt_r
def get_dfbt_x(self):
return self.df_bt_x
def backtest(self):
date_init = self.df.index.values[self.window_size]
df_bt = pd.DataFrame([[0.0, np.nan]], index=[date_init], columns=['ror', 'std'])
df_bt_r = pd.DataFrame(columns=list(self.df.columns.values))
df_bt_x = pd.DataFrame(columns=list(self.df.columns.values))
for idx, date in enumerate(self.df.index.values):
if idx >= self.window_size + self.rebalance_freq:
if (idx - self.window_size) % self.rebalance_freq == 0:
# df_chg_train
st = idx - self.rebalance_freq - self.window_size
ed = idx - self.rebalance_freq
df_chg_train = self.df_chg[st:ed]
# expected returns per target term
if isinstance(self.r_e, pd.core.frame.DataFrame):
r_e = self.r_e.iloc[st:ed].values.mean()
else:
r_e = self.r_e
# x_p: min variance portfolio
x_p = self.calc_portfolio(df_chg_train, r_e)
# df_chg_test
st = idx - self.rebalance_freq
ed = idx
df_chg_test = self.df_chg[st:ed]
df_chgcum_test = (1.0 + df_chg_test).cumprod() - 1.0
# ror_p: rate of return (portfolio)
ror_test = df_chgcum_test.iloc[-1].values
ror_p = float(np.dot(ror_test, x_p))
df_bt_r.loc[date] = ror_test
df_bt_x.loc[date] = x_p
# std (portfolio)
if self.rebalance_freq == 1:
std_p = np.nan
else:
std_test = df_chg_test.std(ddof=True).values
std_p = float(np.dot(std_test, np.abs(x_p)))
# append
df_one = pd.DataFrame([[ror_p, std_p]], index=[date], columns=df_bt.columns)
df_bt = df_bt.append(df_one)
# reset index
self.df_bt = self._reset_index(df_bt)
self.df_bt_r = self._reset_index(df_bt_r)
self.df_bt_x = self._reset_index(df_bt_x)
return self.df_bt
def calc_portfolio(self, df_retchg, r_e):
r = df_retchg.mean().values
cov = np.array(df_retchg.cov())
x_opt = self.cvxopt_qp_solver(r, r_e, cov)
return x_opt
def cvxopt_qp_solver(self, r, r_e, cov):
"""
CVXOPT QP Solver for Markowitz' Mean-Variance Model
- See also https://cvxopt.org/userguide/coneprog.html#quadratic-programming
- See also https://cdn.hackaday.io/files/277521187341568/art-mpt.pdf
r: mean returns of target assets. (vector)
r_e: min of the return ratio (= capital gain / investment).
cov: covariance matrix of target assets. (matrix)
"""
n = len(r)
r = cvxopt.matrix(r)
# Create Objective matrices
P = cvxopt.matrix(2.0 * np.array(cov))
q = cvxopt.matrix(np.zeros((n, 1)))
# Create constraint matrices
G = cvxopt.matrix(np.concatenate((-np.transpose(r), -np.eye(n)), 0))
h = cvxopt.matrix(np.concatenate((-np.ones((1,1))*r_e, np.zeros((n,1))), 0))
A = cvxopt.matrix(1.0, (1, n))
b = cvxopt.matrix(1.0)
# Adjust params (stop log messages)
cvxopt.solvers.options['show_progress'] = False # default: True
cvxopt.solvers.options['maxiters'] = 1000 # default: 100
sol = cvxopt.solvers.qp(P, q, G, h, A, b)
x_opt = np.squeeze(np.array(sol['x']))
return x_opt
def get_yearly_performance(self):
if self.df_bt is None:
pass
else:
df_yearly = self.df_bt[["ror"]].resample('y').sum()
df_yearly["std"] = self.df_bt["ror"].resample('y').std().values
df_yearly["sharpe_ratio"] = df_yearly.apply(lambda d: (d["ror"] - self.r_f) / d["std"], axis=1)
return df_yearly
def evaluate_backtest(self, logging=False):
if self.df_bt is None:
pass
else:
self.r_mean = self.df_bt["ror"].mean()
self.r_std = self.df_bt["ror"].std(ddof=True)
self.sharpe_ratio = (self.r_mean - self.r_f) / self.r_std
self.net_capgain = (self.df_bt["ror"] + 1.0).cumprod().iloc[-1] - 1.0
self.r_mean_peryear = 12 * self.r_mean
self.r_std_peryear = np.sqrt(12) * self.r_std
self.sharpe_ratio_peryear = (self.r_mean_peryear - self.jgb_int) / self.r_std_peryear
if logging:
print("Portfolio Performance")
print("=======================")
print("Returns per month")
print(" sharpe ratio : {:.8f}".format(self.sharpe_ratio))
print(" mean of returns : {:.8f}".format(self.r_mean))
print(" std of returns : {:.8f}".format(self.r_std))
print(" risk-free rate : {:.8f}".format(self.r_f))
print(" capgain ratio : {:.8f}".format(self.net_capgain))
print("Returns per year")
print(" sharpe ratio : {:.8f}".format(self.sharpe_ratio_peryear))
print(" mean of returns : {:.8f}".format(self.r_mean_peryear))
print(" std of returns : {:.8f}".format(self.r_std_peryear))
def plot_returns(self):
if self.df_bt is None:
pass
else:
xlabels = [d.strftime('%Y-%m') for idx, d in enumerate(self.df_bt.index) if idx % 12 == 0]
fig, ax = plt.subplots(figsize=(12,6))
ax.plot(self.df_bt.index.values, self.df_bt["ror"].values, label="rate of returns")
ax.plot(self.df_bt.index.values, self.df_bt["ror"].cumsum().values, label="total capital gain ratio")
ax.legend(loc="upper left")
ax.set_xticks(xlabels)
ax.set_xticklabels(xlabels, rotation=40)
return fig
def plot_returns_histgram(self):
if self.df_bt is None:
pass
else:
x = self.df_bt["ror"].values
r_mean = "{:.4f}".format(x.mean())
r_std = "{:.4f}".format(x.std())
fig, ax = plt.subplots(figsize=(12,6))
ax.hist(x, bins=30, alpha=0.75)
ax.set_title(f"mean={r_mean}, std={r_std}")
return fig
使い方
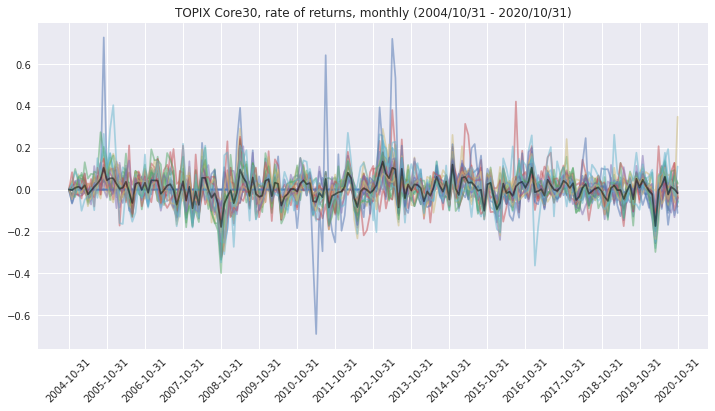
対象資産としてTOPIX Core30に含まれる内国株30銘柄を選び,これらに(最適な)投資比率を与えてバックテストしてみましょう.
ヒストリカルデータの準備
まず,pandas_datareader.data.DataReaderでTOPIX Core30構成銘柄のヒストリカルデータを読み込んで,すこし整形します.1
# Get historical data
st = '2004/10/31' # start date
ed = '2020/10/31' # end date
stocks_topix30 = [2914, 3382, 4063, 4452, 4502,
4503, 5401, 6301, 6501, 6502,
6752, 6758, 6954, 7201, 7203,
7267, 7751, 8031, 8058, 8306,
8316, 8411, 8604, 8766, 8802,
9021, 9432, 9433, 9437, 9984] # list of tickers in TOPIX Core30
symbols = [str(s)+'.T' for s in stocks_topix30]
dfs = []
for symbol in symbols:
df = pandas_datareader.data.DataReader(symbol, 'yahoo', st, ed) # daily
df = df.resample('M').mean() # daily -> monthly
df = df.sort_values(by='Date', ascending=True)
df = df.fillna(method='ffill') # 1つ前の行の値で埋める
df = df[['Close']].rename(columns={'Close': symbol})
dfs.append(df)
df_tpx30 = pd.concat(dfs, axis=1)
# fill nan
for col in df_tpx30.columns:
st_idx = df_tpx30[col].first_valid_index()
ed_idx = df_tpx30[col].last_valid_index()
# for any columns (stocks)
if df_tpx30[col].isnull().any():
# New listing (新規上場)
if st_idx != df_tpx30.index[0]:
df_tpx30[col] = df_tpx30[col].fillna(df_tpx30[col][st_idx])
# Delisting (上場廃止)
if df_tpx30.index[-1] != ed_idx:
df_tpx30[col] = df_tpx30[col].fillna(df_tpx30[col][ed_idx])
こんな感じのパネルデータができれば準備OK.
df_tpx30.tail()
Date 2914.T 3382.T 4063.T 4452.T 4502.T 4503.T 5401.T 6301.T 6501.T 6502.T ... 8316.T 8411.T 8604.T 8766.T 8802.T 9021.T 9432.T 9433.T 9437.T 9984.T
2020-06-30 2147.159091 3710.272727 12471.136364 8774.045455 4024.818182 1824.386364 1063.240909 2220.500000 3561.590909 3275.681818 ... 3172.181818 1363.545455 486.763636 4795.681818 1701.840909 6502.181818 2500.454545 3184.863636 2913.454545 5287.318182
2020-07-31 1933.785714 3427.333333 12802.619048 8465.428571 3763.000000 1731.785714 998.023810 2239.047619 3371.714286 3450.714286 ... 3029.809524 1347.857143 491.138096 4699.238095 1576.000000 5405.428571 2523.428571 3289.142857 2944.547619 6311.333333
2020-08-31 1995.300000 3399.050000 12785.500000 8041.000000 3967.150000 1712.075000 1009.300000 2207.650000 3489.050000 3351.750000 ... 3023.050000 1402.250000 531.764998 4779.850000 1644.575000 5106.050000 2570.875000 3285.300000 3066.400000 6453.700000
2020-09-30 1970.425000 3357.000000 13804.250000 8053.550000 3898.200000 1622.550000 1073.164999 2352.600000 3631.650000 2941.300000 ... 3090.425000 1402.175000 522.770003 4871.900000 1638.575000 5578.100000 2313.800000 2851.150000 2879.875000 6278.600000
2020-10-31 1989.095238 3412.714286 14189.761905 7731.619048 3568.904762 1489.047619 1070.538095 2432.285714 3605.000000 2783.952381 ... 2969.428571 1311.571429 487.642857 4804.000000 1611.214286 4938.571429 2237.142857 2742.738095 3882.095238 6991.047619
モデル学習(パラメータ設定)
あとは,自作クラスMarkowitzMinVarianceModel()のインスタンスオブジェクトmodelにパラメータと価格データdf_tpx30を食わせてバックテストを実行.
from datetime import datetime
# Const.
ST_BACKTEST = datetime(2011,10,31) # Investment period (start date)
ED_BACKTEST = datetime(2020,10,31) # Investment period (end date)
# Params
params = {
"window_size": 36, # 収益率の特性量(平均,分散)の推定に使う期間 (例: 運用時から過去36カ月)
"rebalance_freq": 1, # リバランスの頻度 (1か月ごとにポートフォリオ内の投資比率を変更)
"r_f": 0.0001 * (1/12) # リスクフリーレート (日本国債10年物利回り:0.01%を単利計算で月次に変換)
}
# Data
st = (ST_BACKTEST - relativedelta(months=params["window_size"])).strftime('%Y-%m-%d')
ed = ED_BACKTEST.strftime('%Y-%m-%d')
df = df_tpx30[st:ed]
params["r_e"]= df_tpx[st:ed] # 要求期待収益率(r_e)は同時期のTOPIX Indexの収益率とする (df_tpx作成コードは省略)
# Create model
model = MarkowitzMinVarianceModel(df, **params)
# Backtest by model
df_bt = model.backtest()
ここからは,自作クラスMarkowitzMinVarianceModel()に用意したバックテスト評価用のメソッドを使う.(分析は無限大)
ポートフォリオのパフォーマンス評価
# Evaluate
model.evaluate_backtest(logging=True)
Portfolio Performance
=======================
Returns per month
sharpe ratio : 0.18788996
mean of returns : 0.00735206
std of returns : 0.03908527
risk-free rate : 0.00000833
capgain ratio : 1.04714952
Returns per year
sharpe ratio : 0.65086993
mean of returns : 0.08822476
std of returns : 0.13539535
ポートフォリオの収益率・累積収益率プロット
fig = model.plot_returns() # Plot returns
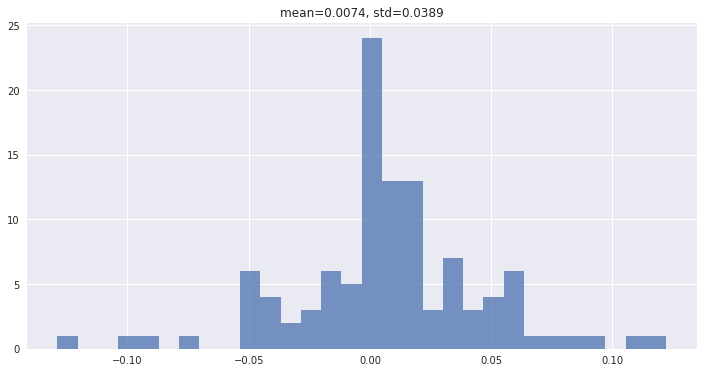
ポートフォリオの月次収益率分布
fig = model.plot_returns_histgram()
ポートフォリオの年次パフォーマンス
df_yearly = model.get_yearly_performance()
df_yearly
date ror std sharpe_ratio
2011-12-31 -0.0001 3.3888e-05 -3.6736
2012-12-31 -0.0444 1.2435e-02 -3.5695
2013-12-31 0.5524 6.5010e-02 8.4973
2014-12-31 0.2448 5.2800e-02 4.6357
2015-12-31 0.0952 4.1543e-02 2.2923
2016-12-31 -0.0970 4.0639e-02 -2.3871
2017-12-31 0.2486 3.0262e-02 8.2144
2018-12-31 -0.0097 3.6705e-02 -0.2644
2019-12-31 0.0254 3.1904e-02 0.7947
2020-12-31 -0.1793 7.3461e-02 -2.4404
ポートフォリオ内の各銘柄の収益率(%)
最適ポートフォリオで10年運用した場合の収益率を銘柄別に確認します。
df_bt_r = model.get_dfbt_r() # rate_of_returns
df_bt_x = model.get_dfbt_x() # investment_ratio
df1 = df_bt_r * df_bt_x # (rate_of_returns) × (investment_ratio)
df1 = df1.resample("y").sum()
df1.columns = [c.replace(".T", "") for c in df1.columns]
df1 = df1.T * 100 # transpose && convert as pct.
df1.columns = [c.strftime('%Y') for c in df1.columns]
plt.figure(figsize=(12,12))
sns.heatmap(df1, cmap="RdBu", center=0, annot=True, fmt=".2f", cbar=True)
plt.show()
10年間のパフォーマンス貢献度をみると、
-
JR西日本<9021>は、2013年に19.7%プラス、2020年に8.7%マイナスと、最もボラティリティ高い -
キャノン<7751>やNTT<9432>もCore30銘柄の中で比較的変動大きい。 - 2018年は通信セクター下落(
NTT<9432>・KDDI<9433>・NTTドコモ<9437>)だが、SBG<9984>は横ばい。 - 2020年はほとんどの銘柄マイナスの中、
ソニー<6758>は堅調で分散が機能している。
という傾向です。日本の大型株30銘柄のみでは、分散効果が物足りないように見えます。
最後まで読んでいただき,ありがとうございます!
参考書籍
- http://www.amazon.co.jp/exec/obidos/ASIN/4873118905/yumaloop-22/
- http://www.amazon.co.jp/exec/obidos/ASIN/4873118905/yumaloop-22/
-
stocks_topix30はTOPIX Core30構成銘柄の証券コードのリストです.構成銘柄は毎年10/31に更新されます.サンプルコードを再現したい場合stocks_topix30 = [2914, 3382, 4063, 4452, 4502, 4503, 5401, 6301, 6501, 6502, 6752, 6758, 6954, 7201, 7203, 7267, 7751, 8031, 8058, 8306, 8316, 8411, 8604, 8766, 8802, 9021, 9432, 9433, 9437, 9984]としてください. ↩