CVXOPTで2次計画問題を解く〜ポートフォリオ最適化の例〜
CVXOPTは凸最適化問題を解くPythonのフリーのライブラリです.
今回は,ポートフォリオ最適化を例にして,CVXOPTで2次計画問題を実装してみます.
比較として,SciPyを用いた例は,Scipyで2次計画問題を解く〜ポートフォリオ最適化の例〜をご覧ください.
準備
CVXOPTをインストールする
CVXOPT Installation instructionsを参考にしてください.
pip install cvxopt
データの準備
今回用いるCVXOPT以外のライブラリをインポートします.
import numpy as np
import pandas as pd
import pandas_datareader.data as pdr
import matplotlib.pyplot as plt
%matplotlib inline
今回の例では,Kenneth R. French教授のData Libraryの30業種ポートフォリオのデータを用います.
name = '30_Industry_Portfolios'
df_dict = pdr.DataReader(name=name, data_source='famafrench')
df = df_dict[0]
期待リターン(収益率)を計算します.
mean = df.mean()
リスク(分散共分散行列)を計算します.
cov = df.cov()
std = np.sqrt(np.diag(cov))
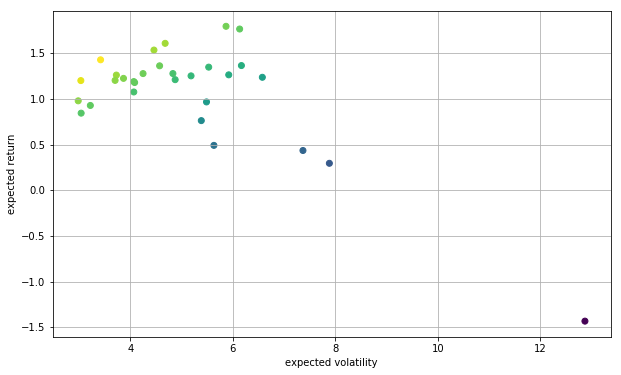
各資産を標準偏差と期待リターンでプロットし,シャープレシオ(リスクフリーレートは考慮しない)で色付けします.
plt.figure(figsize=(10, 6))
plt.scatter(std, mean, c=mean/std, marker='o')
plt.grid(True)
plt.xlabel('expected volatility')
plt.ylabel('expected return')
CVXOPTで二次計画問題を解く
H.M.Markowitzの平均・分散モデル
cvxopt.solvers.qp()を使う
from cvxopt import matrix
from cvxopt.solvers import qp
CVXOPT Quadratic Programmingを確認すると,qpの引数はP, q, G, h, A, bがあります.よって,ポートフォリオ最適化問題を以下の形式に整理して,行列を求める必要があります.その分,SciPyより手間がかかります.
\begin{align}
\min \quad & \frac{1}{2} {\bf x}^T P {\bf x} + {\bf q}^T {\bf x} \\
{\rm subject \: to} \quad & G {\bf x} \leq {\bf h} \\
& A {\bf x} = {\bf b} \\
\end{align}
目標リターン:自分で決める
目標リターンを設定します.
目標リターンは,投資家が恣意的に決めますが,今回は個々の資産の期待リターンの水準を参考に決めます.
tret = mean.mean() # e.g.: tret = 0.5
目的関数
目的関数はポートフォリオの分散なので,Pは分散共分散行列になります.cvxopt.solvers.qpの引数はcvxopt.matrix型にする必要があります.
P = matrix(np.array(cov))
目的関数はポートフォリオの分散なので,qはすべての要素が0の列ベクトルです.なお,「0」とするとmatrixのtc='i'の整数となってしまうため,「0.0」としてtc='d'となるようにします.
q = matrix([0.0] * len(mean))
制約条件
Aとbは投資比率の和が1となる等式制約に当たります.Aは要素がすべて1.0の行ベクトルになります.
A = matrix(1.0, (1, len(mean)))
投資比率の和が1なので,bは1.0です.
b = matrix(1.0)
不等式制約はポートフォリオの期待リターンが目標リターン以上となる制約と下限制約にあたります.$G$は以下のようになります.
\begin{eqnarray}
G = \left(
\begin{array}{ccc}
1 & \cdots & 0 \\
\vdots & \ddots & \vdots \\
0 & \cdots & 1 \\
-r_1 & \cdots & -r_n
\end{array}
\right)
\end{eqnarray}
G = matrix(np.c_[-np.identity(len(mean)), np.array(-mean)].T)
hは下限0と目標リターン$r_G$の列ベクトルになります.
$$h=(0,\cdots,0,-r_G)^T$$
h = matrix(np.r_[np.zeros(len(mean)), np.array(-tret, ndmin=1)])
まとめると,次のようになります.
tret = mean.mean()
P = matrix(np.array(cov))
q = matrix([0.0] * len(mean))
A = matrix(1.0, (1, len(mean)))
b = matrix(1.0)
G = matrix(np.c_[-np.identity(len(mean)), np.array(-mean)].T)
h = matrix(np.r_[np.zeros(len(mean)), np.array(-tret, ndmin=1)])
最適化
最適化を実行します.
%%time
sol = qp(P=P, q=q, G=G, h=h, A=A, b=b)
pcost dcost gap pres dres
0: 1.9211e+00 1.3849e+00 5e+01 6e+00 2e+01
1: 2.2276e+00 1.8570e+00 7e+00 9e-01 2e+00
2: 2.9679e+00 2.7243e+00 2e+00 2e-01 4e-01
3: 3.2479e+00 3.1472e+00 2e-01 1e-02 3e-02
4: 3.2302e+00 3.2133e+00 2e-02 3e-04 8e-04
5: 3.2202e+00 3.2188e+00 1e-03 9e-06 2e-05
6: 3.2192e+00 3.2191e+00 1e-04 5e-08 1e-07
7: 3.2191e+00 3.2191e+00 9e-06 4e-11 1e-10
8: 3.2191e+00 3.2191e+00 3e-07 2e-13 4e-13
Optimal solution found.
CPU times: user 4.7 ms, sys: 2.26 ms, total: 6.96 ms
Wall time: 5.28 ms
最適投資比率を確認します.
list(sol['x'])
最適値(ポートフォリオの分散)を確認します.
2 * sol['primal objective']
6.438220501299366
効率的フロンティアを描く
目標リターンを複数パターン作ります.
mean_high = mean.max().round(3)
mean_low = round(mean.quantile(0.25), 3)
trets = np.linspace(mean_low, mean_high, 50)
各目標リターンについて,最適化を実行します.
%time
tvols = []
for tret in trets:
h = matrix(np.r_[np.zeros(len(mean)), np.array(-tret, ndmin=1)])
sol = qp(P=P, q=q, G=G, h=h, A=A, b=b)
tvols.append(np.sqrt(2 * sol['primal objective']))
tvols = np.array(tvols)
CPU times: user 2 µs, sys: 1 µs, total: 3 µs
Wall time: 4.77 µs
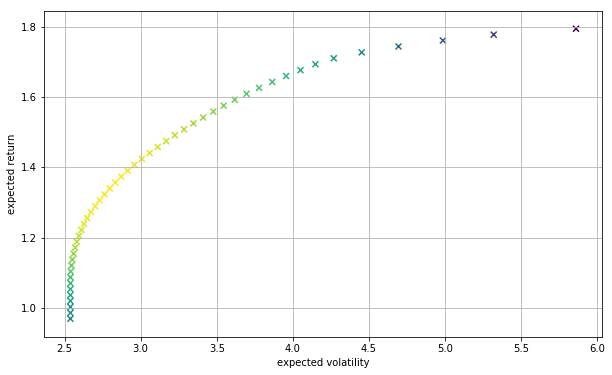
効率的フロンティアを描きます.
plt.figure(figsize=(10, 6))
plt.scatter(tvols, trets, c=trets/tvols, marker='x')
plt.grid(True)
plt.xlabel('expected volatility')
plt.ylabel('expected return')
SciPyとの比較
今回の例では決定変数30個だけですが,CVXOPTのほうがかなり速いです.
| 計測方法 | SciPy | CVXOPT |
|---|---|---|
| %%time | 65.8ms | 6.16ms |
| %%timeit | 44.6ms | 4.49ms |
免責事項
- 本内容はポートフォリオ理論や数理計画問題の一般論であり,投資を勧めるものでは一切ありません.
- 本投稿で計算した数値は仮定のものであり,その数値に一切責任は負いません.
- 本内容は個人の見解であり,所属組織とは一切関係ありません.