LoginSignup
202
193

More than 5 years have passed since last update.

@yukiB(Yuki BAN)in株式会社テンクー

TensorFlowのRNNを基本的なモデルで試す

Last updated at Posted at 2016-05-29

TensorFlowにもRNN(Reccurent Neural Network) が実装されており，Tutorialもあるものの，例題自体が言語モデルを扱った少し複雑なもので，初学者にはとっつきにくいなと感じました．

今回は言語モデルでない，より単純なモデルを扱う問題を例に挙げ，TensorFlowでのRNN実装を試します．

注意

TensorFlowのバージョンがあがり，動かなくなっている部分があるので，こちら(TensorFlow RNN関連のimportやBasicLSTMCellでエラーが出た場合の対処(v 0.11r~))
もみてみてください．

環境

  • OSX
  • python 2.7.11
  • TensorFlow r0.8

SimpleなRNN

SimpleなRNNのモデルや，その実装方法としてはPeter's noteというブログが大変参考になるので，初めての場合はそちらをまず読んでみることをお勧めします．上記サイトからRNNの図を引用すると，

rnn

のようになっています．

つまり，入力層ユニットxからのデータに重みW_xを乗じた後，隠れ層ユニットsに入る，ユニットsの出力に対しては再帰がかかり，重みW_recをかけた結果が次のステップのユニットsに入る．上図右の展開された状態を考えると，隠れ層ユニットの初期値s_0の状態は，ステップが進行するにつれ重みW_recを乗じながら状態を変異させていく．その際，各ステップにおいてxが入力され，最終ステップのs_nの状態が出力層ユニットyに出力される．

といった流れになっています．

数列の合算値を求める

Peter's noteのRNNモデルでは，X_k = 0. or 1.の数値が入力された際の，それらの合計値を出力するネットワークモデルとなっています．

たとえば，

X = [0. 1. 1. 0. 1. 0. 0. 1. 0. 0.]

という入力があった場合，このリストの合算値である

Y = 2.

を正しい出力とするモデルです．単純に足し算してしまえばすぐに結果がでるモデルですが，今回はこれをRNNで学習させることによって求めます．

LSTM

とはいえ，TensorFlowのRNN Toutorialで使われているのはシンプルなRNNではなくLSTM(Long-Short Term Memory)という手法です．上の図で示した通り，通常のRNNではNNの大きさがステップ数に比例してどんどん大きくなってしまいます．
そのため，誤差逆伝搬法を適応させるために必要な計算量やメモリが多くなり，伝搬される誤差が爆発してしまって計算が安定しないという問題がありました．

それに対しLSTMでは，単純な隠れ層の代わりにLSTMユニットを用いることで，ユニットのコア値（メモリセル値）が次の時刻でどれくらい保持されるか，そして次のステップにどれだけ影響するかを調整することができます．

LSTM

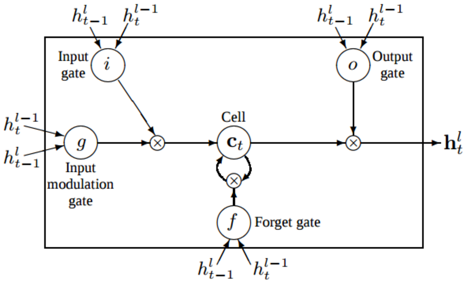
一つのLSTMユニットは上の図のようになっており

  • メモリセル（Cell）・・・過去の状態を表し，C_tで表す．
  • 入力 (input gate)・・・時刻tにおけるl−1番目の隠れ層の出力h^{l−1}_tと時刻t−1におけるl番目の隠れ層の出力h_{t−1}^lからなる．
  • 入力判断ゲート (input modulation gate)・・・メモリセルに加算される値を調整する役割を持つ
  • 忘却判断ゲート (forget gate)・・・メモリセルの値が次の時刻でどれくらい保持されるかを調整する役割を持つ
  • 出力判断ゲート (output gate)・・・メモリセルの値が次の層にどれだけ影響するかを調整する役割を持つ

以上の要素で構成されます．

LSTMの詳しい説明は，Christopher Olah氏のブログ記事（http://colah.github.io/posts/2015-08-Understanding-LSTMs/）にあり，大変勉強になります．

TensorFlowで組んでみる

本来，上記例題であれば，過去の入力が全て等しく現在のステップに作用するため，LSTMを持ち出すまでもありません．ですが，今回はTensoreFlowにデフォルトで実装されているBasicLSTMCellを使って上記の合算例題を試してみます．コードはhttps://github.com/yukiB/rnntestにおきました．

まず，データの作成は，


def create_data(num_of_samples, sequence_len):
    X = np.zeros((num_of_samples, sequence_len))
    for row_idx in range(nb_of_samples):
        X[row_idx,:] = np.around(np.random.rand(sequence_len)).astype(int)
    # Create the targets for each sequence
    t = np.sum(X, axis=1)
    return X, t

によりおこないます．

LSTM層の設計は，


def inference(input_ph, istate_ph):
     with tf.name_scope("inference") as scope:
        weight1_var = tf.Variable(tf.truncated_normal([num_of_input_nodes, num_of_hidden_nodes], stddev=0.1), name="weight1")
        weight2_var = tf.Variable(tf.truncated_normal([num_of_hidden_nodes, num_of_output_nodes], stddev=0.1), name="weight2")
        bias1_var   = tf.Variable(tf.truncated_normal([num_of_hidden_nodes], stddev=0.1), name="bias1")
        bias2_var   = tf.Variable(tf.truncated_normal([num_of_output_nodes], stddev=0.1), name="bias2")

        in1 = tf.transpose(input_ph, [1, 0, 2]) 
        in2 = tf.reshape(in1, [-1, num_of_input_nodes]) 
        in3 = tf.matmul(in2, weight1_var) + bias1_var
        in4 = tf.split(0, length_of_sequences, in3)   

        cell = rnn_cell.BasicLSTMCell(num_of_hidden_nodes, forget_bias=forget_bias)
        rnn_output, states_op = rnn.rnn(cell, in4, initial_state=istate_ph)
        output_op = tf.matmul(rnn_output[-1], weight2_var) + bias2_var
        return output_op

にておこないます．

in3 = tf.matmul(in2, weight1_var) + bias1_var

でLSTMユニット内でのセル更新式を与えています．
また


output_op = tf.matmul(rnn_output[-1], weight2_var) + bias2_var

で全ステップのうち最後のLSTM層から得られた出力に重みとバイアスをかけて，最終的な出力としています．

コストの計算については，今回出力値が連続の値をとる数値のため，MSE(mean square error)を用い，Activation関数は通さずに，そのままユニットのデータを通す設計にしました．


def loss(output_op, supervisor_ph):
    with tf.name_scope("loss") as scope:
        square_error = tf.reduce_mean(tf.square(output_op - supervisor_ph))
        loss_op  =  square_error
        tf.scalar_summary("loss", loss_op)
        return loss_op

精度の評価としては，100個リストと正解の組み合わせを作り，予測結果と正解の差が0.05未満のものの割合を求めました．


def calc_accuracy(output_op, prints=False):
        inputs, ts = make_prediction(num_of_prediction_epochs)
        pred_dict = {
                input_ph:  inputs,
                supervisor_ph: ts,
                istate_ph:    np.zeros((num_of_prediction_epochs, num_of_hidden_nodes * 2)),
        }
        output= sess.run([output_op], feed_dict=pred_dict)

        def print_result (p, q):
            print("output: %f, correct: %d" % (p , q)) 
        if prints:
            [print_result(p, q)  for p, q in zip(output[0], ts)]

        opt = abs(output - ts)[0]
        total = sum([1 if x[0] < 0.05 else 0 for x in opt])
        print("accuracy %f" % (total/float(len(ts))))
        return output

ここまできたら，オプティマイザーを指定し，計算を回していきます．


def training(loss_op):
    with tf.name_scope("training") as scope:
        training_op = optimizer.minimize(loss_op)
        return training_op

random.seed(0)
np.random.seed(0)
tf.set_random_seed(0)

optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)

X, t = create_data(num_of_sample, length_of_sequences)

with tf.Graph().as_default():
    input_ph      = tf.placeholder(tf.float32, [None, length_of_sequences, num_of_input_nodes], name="input")
    supervisor_ph = tf.placeholder(tf.float32, [None, num_of_output_nodes], name="supervisor")
    istate_ph     = tf.placeholder(tf.float32, [None, num_of_hidden_nodes * 2], name="istate")

    output_op, states_op, datas_op = inference(input_ph, istate_ph)
    loss_op = loss(output_op, supervisor_ph)
    training_op = training(loss_op)

    summary_op = tf.merge_all_summaries()
    init = tf.initialize_all_variables()

    with tf.Session() as sess:
        saver = tf.train.Saver()
        summary_writer = tf.train.SummaryWriter("/tmp/tensorflow_log", graph=sess.graph)
        sess.run(init)

        for epoch in range(num_of_training_epochs):
            inputs, supervisors = get_batch(size_of_mini_batch, X, t)
            train_dict = {
                input_ph:      inputs,
                supervisor_ph: supervisors,
                istate_ph:     np.zeros((size_of_mini_batch, num_of_hidden_nodes * 2)),
            }
            sess.run(training_op, feed_dict=train_dict)

            if (epoch ) % 100 == 0:
                summary_str, train_loss = sess.run([summary_op, loss_op], feed_dict=train_dict)
                print("train#%d, train loss: %e" % (epoch, train_loss))
                summary_writer.add_summary(summary_str, epoch)
                if (epoch ) % 500 == 0:
                    calc_accuracy(output_op)

実行結果

https://github.com/yukiB/rnntestにおいたコードでは最終結果を以下のように出力するようにしています．

[0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0]
output: 6.010024, correct: 6
[1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0]
output: 5.986825, correct: 6
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
output: 0.223431, correct: 0
[0.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0]
output: 3.002296, correct: 3
...
accuracy 0.980000

手元の環境では，100個毎のバッチで5000回学習を回した結果精度は98%程度でした．どうやら正しく学習できているようです．

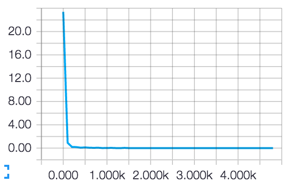
また，コスト関数の収束具合をTensorBoardで確認したところ

image

上記のようになりました．

おわりに

今回は，簡単な合算モデルを通じてTensorFLowのRNN実装をみてみました．オプティマイザーや隠れ層の数等を変えると，収束具合がかなり変わってくるので試してみると面白いです．

参考サイト

202
193
3

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
202
193