Recurrent Neural Network(再帰型ニューラルネット)に関心はあるが,なかなかコード作成に手がつかない,このようなケースが多くないだろうか?理由はいくつかあるが,私の場合は次のようなものが思い当たる.
- 単純にネットワークの構成が複雑.MLP(Multi-layer Perceptron)から入門してCNN(Convolutional-NN)に進むまでは,特殊なLayerがあるにせよ,信号の流れは順方向のみであった.(誤差の計算は除く.)
- MLPやCNNにおいては分かりやすい例題,(Deep Learningの’Hello World'と称される)"MNIST" があったが,そのような標準的な(スタンダードな)例題がRNNにはない.
因みにTheanoのDeep LearningやTensorFlowのTutorialは,言語モデルを扱ったものである.言語モデルに精通されている方はすぐに取りかかれるかもしれないが,初心者はまず「例題が何を解こうとしているか」について理解する必要がある.
今回は,言語モデルでない,より単純な数列を扱う例題を取り上げ,簡単なRecurrent Neural Network(RNN)を実装してみることにした.
(使用したプログラミング環境は,python 2.7.11, Theano 0.7.0になります.)
シンプルなRNN構造
RNNを調べるにあたり,初めに"TensorFlow"のTutorial(ptb_word_lm.py)を動かしてみたが,
"epoch"の数値が増すにしたがい"perplexity"(複雑さ?)の変数が減っていく様子が見られる.しかしながら,それが何を解いているかについては,詳細は理解できなかった.RNNのモデルとしてもLSTM(Long Short-term Memory)を用いているので,これでRNN入門というのは敷居が高いと感じた.
文献「深層学習」ではシンプルなRNNとしてElmanネットが紹介されている.また,"Elman RNN"をキーワードに調べたところ,SimpleなRNNを紹介する"Peter's note"(http://peterroelants.github.io/) というブログが参考になったので,これをベースにプログラムを検討した.
上記サイトからRNNの図を引用する.
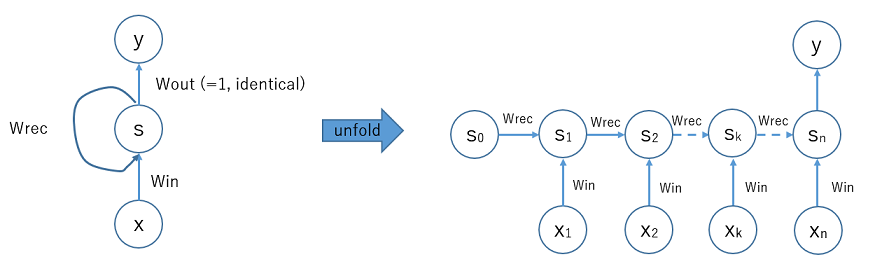
入力ユニットxからデータが入り,重み W_in を乗じた後,隠れ層ユニットsに入る.ユニットSの出力について再帰の流れがあって,重み W_rec をかけた結果が次の時刻にユニットsに戻る.また,出力に対しては通常,重み W_out を考慮する必要があるが,構造をより単純化するために,W_out=1.0 と固定するとユニットSの状態がそのまま出力される構成となる.
左図の状態に対して,BPTT法(Backpropagation through time)を適用するため右側の「展開された」状態を考える.隠れユニットの初期値 s_0 の状態は,時刻が進むにつれ重み W_rec を乗じながら右方向へ状態が遷移する.また各時刻において [x_1, x_2, ... x_n] が入力される.最終時刻に s_n の状態がユニットyに出力される.
以上示したモデルをPythonコードに直すと以下のようになる.("Peter's note" から引用.)
def update_state(xk, sk, wx, wRec):
return xk * wx + sk * wRec
def forward_states(X, wx, wRec):
# Initialise the matrix that holds all states for all input sequences.
# The initial state s0 is set to 0.
S = np.zeros((X.shape[0], X.shape[1]+1))
# Use the recurrence relation defined by update_state to update the
# states trough time.
for k in range(0, X.shape[1]):
# S[k] = S[k-1] * wRec + X[k] * wx
S[:,k+1] = update_state(X[:,k], S[:,k], wx, wRec)
return S
例題はどのような内容か?
また,「上記のRNNモデルでどのような問題を扱っているか」であるが,入力として X_k = 0. or 1.のバイナリーの数値を入力する.出力は,これらのバイナリーの合計値を出力するネットワークモデルとする.例えば,
X = [ 0. 1. 0. 0. 0. 0. 0. 0. 0. 1.] に対して,(このリストXの合計値が2.なので)
Y = 2. の出力が正しい値と設定する.
もちろん,「数値をカウントするというアルゴリズム」は使わずにRNN(含む2つの重み係数)で推定するのが例題の内容である.
出力値が連続の値をとる数値なので,「分類」の問題でなく,「回帰」の問題の一種と考えることができる.したがって,コスト関数としてはMSE(mean square error)を用い,Activation関数は通さず,そのままユニットのデータを通すようにしている.
まず(事前に作成した)Trainデータで学習を行い,2の重み係数[W_in, W_rec]を求めることになるが,上図を見れば容易に推定できるが,正解は [W_in, W_rec] = [1.0, 1.0] である.
モデル実装の事前検討
参考にした"Peter's note"の記事では,Deep Learningのライブラリを用いることなく,python (with numpy) を用いてIPython Notebookにまとめている.これをこのまま写経すれば,ブログ記事通りの結果を得られるが,発展性を考慮してDeep Learningのライブラリを用いる実装を試みた.選択肢として以下を考えた.
- "TensorFlow" を用いる.
- ”Theano" を用いる.
- よりハイレベルな(抽象化した)ライブラリ "Keras", "Pylearn2" 等を用いる.
最初,オリジナルのpythonコードを "one by one" でTensorFlow版にしようと試みたが,
for k in range(0, X.shape[1]):
# S[k] = S[k-1] * wRec + X[k] * wx
S[:,k+1] = update_state(X[:,k], S[:,k], wx, wRec)
return S
の部分のループ処理がうまく(TensorFlow版に)直せないことが分かった.TensorFlowのTutorialコード(ptb_word_lm.pyなど) を参考にすれば,当然今回の簡単なRNNモデルも実装できるはずであるが,関連するクラスライブラリが複雑で理解が難しかったので,今回はTensorFlowの使用を見送った.
また,選択肢3の"Keras", "Pylearn2"等については,「RNNの実装を理解する」という目的から外れるため今回は選ばなかった.
結局,選択肢2の"Theano"版のコードを作成することにした.
RNNのための”Theano scan”
ネットで見かけるTheanoによるRNNコードに共通しているのは,ほとんどのコードで"Theano scan"を用いていることである.Theano scanは,TheanoフレームワークのなかでLoop処理(反復処理),Iteration処理(収束計算)を行うために機能である.仕様が複雑で,また本家ドキュメント(Theano Documentation)を見てもすぐには理解が難しい.日本語情報はかなり限られるが,sinhrks氏のブログ記事を参考に,小さいコードをJupyter Notebookで試しながら,Theano scanの挙動調査を進めた.
n = T.iscalar('n')
result, updates = theano.scan(fn=lambda prior, nonseq: prior * 2,
sequences=None,
outputs_info=a, # 一つ前のLoopにおける値を参照 --> prior
non_sequences=a, # シーケンスでない値 --> nonseq
n_steps=n)
myfun1 = theano.function(inputs=[a, n], outputs=result, updates=updates)
myfun1(5, 3)
# array([10, 20, 40])
# return-1 = 5 * 2
# return-2 = return-1 * 2
# return-3 = return-2 * 2
実行結果:
>>> array([10, 20, 40], dtype=int32)
とても詳細を説明しきれないので,使用例をいくつか取り上げる.theano.scan()は,上記の通り,5種類の引数をとる.
| Key Word | 内容 | 使用例 |
|---|---|---|
| fn | 反復処理のための関数 | fn=lambda prior, nonseq: prior * 2 |
| sequences | 逐次処理の際,要素を進めながら入力を行うList, Matrixタイプの変数 | sequences=T.arange(x) |
| outputs_info | 逐次処理の初期値を与える | outputs_info=a |
| non_sequences | シーケンスでない(反復処理で不変の)固定値 | non_sequences=a |
| n_steps | 繰り返し関数 | n_steps=n |
上のコードでは,theano.scan() に対し,(シーケンスではない)初期値 5 と回数 3 が与えられ,反復処理の度に,前回の処理の結果に対し 2 を乗ずる,という処理を行っている.
1回目の反復処理 : 5 x 2 = 10
2回目の反復処理 : 10 x 2 = 20
3回目の反復処理 : 20 x 2 = 40
この結果,result = [10, 20, 40] と算定されている.
もう少しRNNを意識したテストが以下である.
v = T.matrix('v')
s0 = T.vector('s0')
result, updates = theano.scan(fn=lambda seq, prior: seq + prior * 2,
sequences=v,
outputs_info=s0,
non_sequences=None)
myfun2 = theano.function(inputs=[v, s0], outputs=result, updates=updates)
myfun2([[1., 0.], [0., 1.], [1., 1.]], [0.5, 0.5])
実行結果:
>>> array([[ 2., 1.],
[ 4., 3.],
[ 9., 7.]], dtype=float32)
初期値 [0.5, 0.5] が関数に入力される.$$ fn=\texttt{lambda}\ seq, prior:\ seq + prior * 2$$ と定義したので,
1回目の反復処理 : [1., 0.] + [0.5, 0.5] x 2 = [2., 1.]
2回目の反復処理 : [0., 1.] + [2., 1.] x 2 = [4., 3.]
3回目の反復処理 : [1., 1.] + [4., 3.] x 2 = [9., 7.]
という流れで計算されている.
"theano.scan()" は,RNNで必要な処理のフローコントロールをサポートする機能である.TensorFlowについて同様の機能は現段階でサポートされていないが,
Our white paper mentions a number of control flow operations that we've experimented with
-- I think once we're happy with its API and confident in its implementation we will try
to make it available through the public API -- we're just not quite there yet.
It's still early days for us :)(GitHub TensorFlow issue #208 のdiscussionより引用.)
とのことなので,将来のサポートを待ちたい.
(TensorFlow のRNN modelについてどのような実装が行われているか理解できていませんが,すでにRNNの計算を実現させているということは,このような"theano.scan()"ライクの機能が「必須」ではない,ということを表しています.この件,もう少しTenforFlowのサンプルコードを勉強する必要があると考えています.)
Theanoを用いたSimple RNNのコード詳細
Theano Scan()が分かったところで,Simple RNNのコードを見ていく.まず,simpleRNNのクラスを定義する.
class simpleRNN(object):
# members: slen : state length
# w_x : weight of input-->hidden layer
# w_rec : weight of recurrnce
def __init__(self, slen, nx, nrec):
self.len = slen
self.w_x = theano.shared(
np.asarray(np.random.uniform(-.1, .1, (nx)),
dtype=theano.config.floatX)
)
self.w_rec = theano.shared(
np.asarray(np.random.uniform(-.1, .1, (nrec)),
dtype=theano.config.floatX)
)
def state_update(self, x_t, s0):
# this is the network updater for simpleRNN
def inner_fn(xv, s_tm1, wx, wr):
s_t = xv * wx + s_tm1 * wr
y_t = s_t
return [s_t, y_t]
w_x_vec = T.cast(self.w_x[0], 'float32')
w_rec_vec = T.cast(self.w_rec[0], 'float32')
[s_t, y_t], updates = theano.scan(fn=inner_fn,
sequences=x_t,
outputs_info=[s0, None],
non_sequences=[w_x_vec, w_rec_vec]
)
return y_t
クラスメンバとして,状態(state)の長さと重み(w_x, w_rec)を与えてクラスを定義する.クラスメソッド state_update() は,stateの初期値 s0 と入力系列 x_t が与えられたときにネットワークの状態を更新し,y_t (出力系列) を算定する.y_t はベクトルであるが,メインの処理では,y = y_t[-1] のように最終値のみを取り出してコスト関数の算定に用いる.
メインの処理では,まず学習に用いるデータを作成する.(ほぼ,ネタ元"Peter's note"の通り.)
np.random.seed(seed=1)
# Create Dataset by program
num_samples = 20
seq_len = 10
trX = np.zeros((num_samples, seq_len))
for row_idx in range(num_samples):
trX[row_idx,:] = np.around(np.random.rand(seq_len)).astype(int)
trY = np.sum(trX, axis=1)
trX = trX.astype(np.float32)
trX = trX.T # need 'List of vector' shape dataset
trY = trY.astype(np.float32)
# s0 is time-zero state
s0np = np.zeros((num_samples), dtype=np.float32)
trXが,長さ10の系列データ,20サンプルとなる.ここでポイントは,trX = trX.T とマトリクスを転置させていることである.一般的な機械学習のデータセットとしては,横方向(column)に1つのデータの特徴量を並べ,それを縦方向(row)にサンプル数分,並べることが多いと思われる.
Data Set Shape
feature1 feature2 feature3 ...
sample1: - - -
sample2: - - -
sample3: - - -
.
.
しかしながら,今回は,時系列データを theano.scan() で更新させる際,縦方向にグルーピングしてデータを渡す必要があった.
(以下のようにグループ化することで,theano.scan() の動作と整合性をとる.)
Data Set Shape (updated)
[ time1[sample1, time2[sample1, time3[sample1 ... ]
sample2, sample2, sample2,
sample3, sample3, sample3,
... ] ... ] ... ]
これを簡便に実現するために,マトリクスの転置を行い,theano.scan()への入力として処理している.
この後,Theanoのグラフ,モデル算定値 y_hypo とTrainデータラベル y_ からコスト loss を求めている.
# Tensor Declaration
x_t = T.matrix('x_t')
x = T.matrix('x')
y_ = T.vector('y_')
s0 = T.vector('s0')
y_hypo = T.vector('y_hypo')
net = simpleRNN(seq_len, 1, 1)
y_t = net.state_update(x_t, s0)
y_hypo = y_t[-1]
loss = ((y_ - y_hypo) ** 2).sum()
ここまで来れば,後はお馴染みの方法で学習を進めることができる.
# Train Net Model
params = [net.w_x, net.w_rec]
optimizer = GradientDescentOptimizer(params, learning_rate=1.e-5)
train_op = optimizer.minimize(loss)
# Compile ... define theano.function
train_model = theano.function(
inputs=[],
outputs=[loss],
updates=train_op,
givens=[(x_t, trX), (y_, trY), (s0, s0np)],
allow_input_downcast=True
)
n_epochs = 2001
epoch = 0
w_x_ini = (net.w_x).get_value()
w_rec_ini = (net.w_rec).get_value()
print('Initial weights: wx = %8.4f, wRec = %8.4f' \
% (w_x_ini, w_rec_ini))
while (epoch < n_epochs):
epoch += 1
loss = train_model()
if epoch % 100 == 0:
print('epoch[%5d] : cost =%8.4f' % (epoch, loss[0]))
w_x_final = (net.w_x).get_value()
w_rec_final = (net.w_rec).get_value()
print('Final weights : wx = %8.4f, wRec = %8.4f' \
% (w_x_final, w_rec_final))
今回,オプティマイザは,GradientDecent(勾配降下法)とRMSPropOptimizer(RMSProp法)の2つ用意して用いた.(オプティマイザの部分のコードは,今回省略いたします.RMSProp法については,後に示すWebサイトを参照しました.)
実行結果
「RNNは一般的に学習を進ませるがの難しい」という記述は,いろいろなところで見受けられるが,それを実感させる結果となった.
条件1.勾配降下法(GradientDescent), 学習率= 1.0e-5
Initial weights: wx = 0.0900, wRec = 0.0113
epoch[ 100] : cost =529.6915
epoch[ 200] : cost =504.5684
epoch[ 300] : cost =475.3019
epoch[ 400] : cost =435.9507
epoch[ 500] : cost =362.6525
epoch[ 600] : cost = 0.2677
epoch[ 700] : cost = 0.1585
epoch[ 800] : cost = 0.1484
epoch[ 900] : cost = 0.1389
epoch[ 1000] : cost = 0.1300
epoch[ 1100] : cost = 0.1216
epoch[ 1200] : cost = 0.1138
epoch[ 1300] : cost = 0.1064
epoch[ 1400] : cost = 0.0995
epoch[ 1500] : cost = 0.0930
epoch[ 1600] : cost = 0.0870
epoch[ 1700] : cost = 0.0813
epoch[ 1800] : cost = 0.0760
epoch[ 1900] : cost = 0.0710
epoch[ 2000] : cost = 0.0663
Final weights : wx = 1.0597, wRec = 0.9863
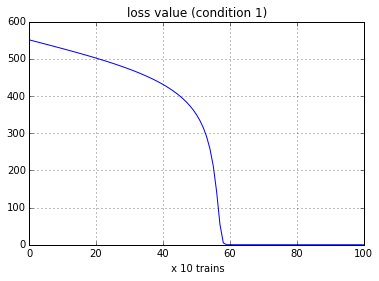
学習の結果,正解 [w_x, w_rec] = [1.0, 1.0] の近似値を得ることができている.下の図は,コスト関数が低減する様子を示している.
Fig. Loss curve (GradientDescent)
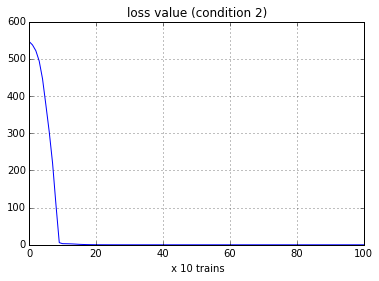
条件2. RMSProp法,学習率=0.001
Initial weights: wx = 0.0900, wRec = 0.0113
epoch[ 100] : cost = 5.7880
epoch[ 200] : cost = 0.3313
epoch[ 300] : cost = 0.0181
epoch[ 400] : cost = 0.0072
epoch[ 500] : cost = 0.0068
epoch[ 600] : cost = 0.0068
epoch[ 700] : cost = 0.0068
epoch[ 800] : cost = 0.0068
epoch[ 900] : cost = 0.0068
epoch[ 1000] : cost = 0.0068
epoch[ 1100] : cost = 0.0068
epoch[ 1200] : cost = 0.0068
epoch[ 1300] : cost = 0.0068
epoch[ 1400] : cost = 0.0068
epoch[ 1500] : cost = 0.0068
epoch[ 1600] : cost = 0.0068
epoch[ 1700] : cost = 0.0068
epoch[ 1800] : cost = 0.0068
epoch[ 1900] : cost = 0.0068
epoch[ 2000] : cost = 0.0068
Final weights : wx = 0.9995, wRec = 0.9993
今回のモデルでは,コスト関数 vs. parameters の非線形性が非常に強いものとなっている.学習率を大きくとるとすぐに数値が発散してしまうため,勾配降下法(Gradient Descent) では,学習率 = 1.0e-5 とかなり小さく設定する必要があった.一方で,RNNに向くと言われるRMSProp法では,学習率 = 0.001 でも問題なく学習を進めることができている.
(補足)
参考にした "Peter's note" のブログでは,コスト関数の状況とRMSProp(引用元のブログでは"Rprop"という呼び名)について詳しい説明が掲載されています.コスト関数の非線形性が色の濃淡でVisual化されていますので関心のある方は参照してみてください.(下リンクになります.)
参考文献 (web site)
- Peter's note - How to implement a recurrent neural network
http://peterroelants.github.io/ - Python Theano function / scan の挙動まとめ - StatsFragments(sinhrksさんブログ)
http://sinhrks.hatenablog.com/entry/2015/04/25/233025 - Theano scan - Looping in Theano
http://deeplearning.net/software/theano/library/scan.html - Theano optimizers - Gist/ kastnerkyle/opimizers.py
https://gist.github.com/kastnerkyle/816134462577399ee8b2
(RMSProp法オプティマイザーの実装例です.今回,これを参考にさせていただきました.) - 深層学習,講談社機械学習プロフェッショナルシリーズ
- 今一度Theanoの基本を学ぶ - Qiita
http://qiita.com/TomokIshii/items/1f483e9d4bfeb05ae231