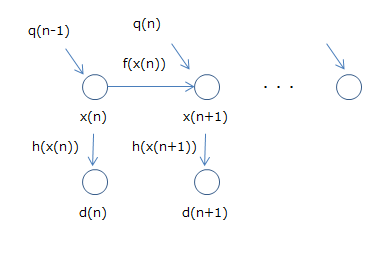ニューラルネットワークで時系列データを扱う場合、リカレントニューラルネットワークを使用します。今回は、そのリカレントニューラルネットワークについての解説です。
(長いため、以下ニューラルネットワークはNN、リカレントニューラルネットワーク(Recurrent Neural Network)はRNNと略記)
RNNの概要
データの中には、「x」が出たら「y」が来る可能性が高い、というように前のデータが次のデータに対し相関を持つものがあります。
具体的には、言葉や音楽といったものです(「私」の後には「は」か「が」が来ることが多い、など)。こうした時系列で相関を持つデータでは、当然前に発生したデータを考慮したくなります。
NNに、前に発生したデータを投入できるようにはできないか。その答えが、RNNとなります。
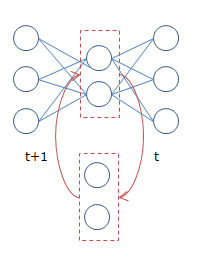
具体的には、下図のようになります。
時刻$t$の隠れ層の内容が、次の時刻$t+1$の時の入力として扱われます。$t+1$の隠れ層が$t+2$の・・・と続くわけですが、要は前回の隠れ層が次の隠れ層の学習にも使用される、というイメージです。
RNNの種別
| 名称 | 結合対象 | 特徴 |
|---|---|---|
| Fully recurrent network | 全ノード(1:N) | 自身も含め完全双方向に結合する |
| Hopfield network | 全ノード(1:N-1) | 双方向結合で、結合対象に自身は含まない |
| Elman network | 1:1 (隠れ層->隠れ層) | 入力層・コンテキスト(隠れ層)・出力層の3層構造 |
| Jordan network | 1:1 (出力層->隠れ層) | 入力層・コンテキスト(隠れ層)・出力層の3層構造 |
| Echo state network (ESN) | 1->1? | 結合対象は、ノードの集合(reservoir)からランダムに決定される |
| Long short term memory network (LSTM) | - | RNNのノードの代わりに、入力値を保持しておけるBlockを採用したもの。高精度 |
| Bi-directional RNN (BRNN) | - | 双方向(過去->未来/未来->過去)のRNNを組み合わせたもの |
Hopfield networkは、一般的なクラス分類以外に最適化問題への応用が可能なモデルです。
Elman/Jordanは、Simple recurrent networksと言われているように一番シンプルな形となっています。RNNを利用したい場合はまずどちらかでやってみて、精度的な問題があるのなら他の手法に切り替えてみる、というのがよいのではないかと思います。
Elman/Jordanの違いは上記のとおりですが(前回データの反映が隠れ層から行われるか、出力層から行われるか)、こちらにも詳しく書かれています。精度的な優劣はありませんが、隠れ層の数によって次に伝播する量を変化させられるElmanの方が柔軟と言えると思います。
Echo state networkは毛色が違ったモデルで、ノードを事前に結合せずReservoir(貯水池などの意味)と呼ばれるプールに貯めておき、入力が与えられた後ランダム/動的に結合を行うというスタイルです。要は人の脳の中ではあらかじめ決められた結合などないわけだから、それを模倣し流動的に結合する・・・というコンセプトで作られたものです。これはLiquid State Machines(直訳すると液状機構)とも呼ばれているようです。
Long short term memory network (LSTM) と Bi-directional RNN (BRNN) は結合方法に関する制約は特にありません。
LSTMは単純なノードの代わりに重みを覚えておけるLSTM blockを採用したものです。これはRNNにおける学習の課題を解決するためのもので、後で解説します。
Bi-directional RNNは過去→未来という一方向の学習だけでなく、未来→過去というある意味負の方向の時系列についても学習を行うことで精度を高められる、というものです。
RNNの学習
RNNの学習については以下のドキュメントが非常に丁寧に書かれています。英語ですが、現段階(2015/1)でRNNに関する日本語文献はほとんど存在しないので、もうあきらめて読む以外にすべはないです。
RNNの学習は一般的に収束が非常に遅いです。精確を期すにはlerning rateを低めにする必要がありますが、低めにするとただでさえ遅い収束がより遅くなります。これはトレードオフになりますが、解決の方法として勾配の不安定性を最適化のプロセスの中で考慮する方法があるそうです(詳しくはEFFICIENT SECOND-ORDER LEARNING ALGORITHMS FOR DISCRETE-TIME RECURRENT NEURAL NETWORKS参照)。
一つ言えるのは、色々調べましたが現時点(2015/1)においてRNNの学習で精度・速度ともに問題のない確立した手法はまだ存在せず、よって当然それを実装したライブラリもないということです。ここは地道に修行を重ねる必要があります。
BPTT (BackPropagation Through Time)
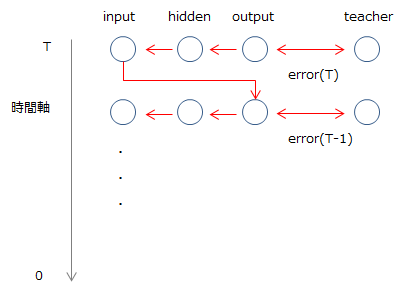
RNNは展開すると長いNNとみなすことができるので、通常通りbackpropagationが適用できるはず、というのが基本的な考え方です。イメージ的には以下のようになります。
誤差は最後の時刻であるTから最初の0に向かって伝播していきます。よって、ある時刻tにおけるoutput layerの誤差は「時刻tにおけるteacher(教師データ)とoutput(出力)の差異」と「t+1から伝播してきた誤差」の和になります。
図からも明らかなとおり、BPTTは最後のTまでのデータ、つまりすべての時系列データがなければ学習を行うことができません。そのため、長いデータは最新の分のみ切り取るなどといった対応が必要です。
このBPTTには様々な課題があり、よってそれに対応するための学習方法もいろいろ考案されています。
LSTM(Long short term memory)
Tがあまりに大きい、つまり長い時系列のデータの場合、計算上の問題で上層からの誤差が薄まったり逆に非常に大きくなったりします(これは、こちらに詳しいです(p8~))。
値が大きくなる分には最大値の制限で何とかなりますが、消えてしまうのはどうにもならないため、誤差が減衰しないよう伝播させるというのがLSTMの思想です。
teacher forcing
RNNではtの出力がt+1のinputになり・・・と続いていきますが、学習時においてはt+1への入力の正解がteacherから明らかなので、それをそのまま使用してしまうという方法です。これにより各層で下層からの影響を無視して学習させることができ、収束速度を上げることができますが、(学習後)実際実行すると出力が安定しない?ようです。
RPROP(Resilient backpropagation)
これは通常のNNでも使用される方法です。NNを学習させる際勾配を計算しますが、その勾配の向き(sign)が前回と今でどのように変化したかによって重み($\eta$)をかけるものです(詳細はこちらに詳しいです。)。
- 前回と今回で符号が同じ場合、勾配に重みをかけることで学習を加速させる。
- 前回と今回で符号が異なる場合、勾配を減速させ見過ごした最適解に戻る。
この挙動が、ちょうどボールを転がしているような感じになるため(勾配で加速し、勾配の向きが変わるとゆっくりになり逆向きの力が働く)、Resilientという名前がついているのだと思います。
Sigmoid関数のような関数では値が一定範囲を超えた箇所ではフラット(勾配がほぼ0)になるため学習が進みにくくなりますが(Flat Spot Problem)、この手法を適用することで重みがかかるため学習の停滞を防ぐ効果もあります。
この手法自体にもさまざまなバリエーションがあります。詳しくはこちらをご参考ください。
上記の様々な手法以外に、通常のNN同様、誤差伝播の度合いを調整するlearning rate、ひとつ前の層の影響度を調整するmomentumといったパラメーターのチューニングも重要です。
BPTTは一般的に収束が遅く学習に時間がかかります。そのため、隠れ層のノードが3~20程度の小さなネットワークで使われることが多く、これを超える場合数時間、またそれ以上の学習時間がかかる恐れがあります。
RTRL (Real Time Recurrent Learning)
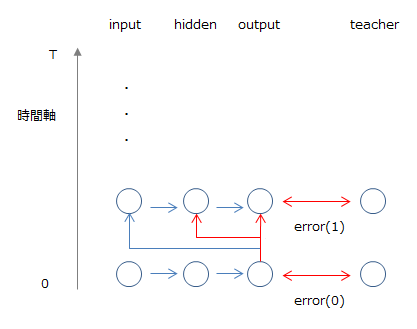
RTRLはBPTTとは異なり誤差を先の時間に伝播していく方法であり、このためオンライン学習に適しています。
時刻tで発生した誤差で、次の時刻t+1の重みを更新します。上の図では各時間で誤差を計算し伝播させていますが、一定時間(epoch)の後に更新するという手法もあります。ただ、一度に更新しなければならない重みがBPTTに比べ多いため、計算負荷が高くなります。
EKF (Extended Kalman Filter)
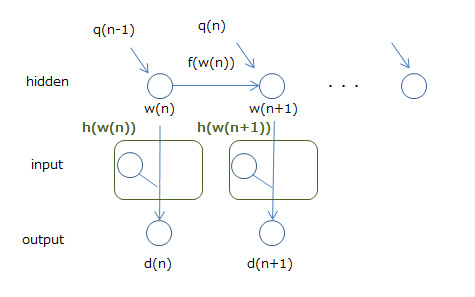
RNNに拡張カルマンフィルタを適用し、重みの更新を行うのがEKFです。拡張カルマンフィルタは線形の系を扱うカルマンフィルタを非線形に拡張したもので、以下のように系の状態を推定します。
$ x(n+1) = f(x(n)) + q(n) $
$ d(n) = h_n(x(n)) $
上記の数式は、以下のことを表現しています。
- 次の状態$x(n+1)$は前の状態$x(n)$からの入力$f(x(n))$と、$q(n)$(外部からのノイズを表現したもの)で決まる
- 状態$x(n)$の出力は$h_n(x(n))$
イメージ的には下図のようになります。
そして、RNNはこの拡張カルマンフィルタとみなせる、とします。それを表したのが以下の図です。
重み$w$を状態、出力を$d$とするところは問題ないと思います。問題なのはinputですが、これを出力$d$を計算するための関数$h$の中の一部とみなしてしまうことで、これは拡張カルマンフィルタだ、ということにします(実際inputの入力と重み$w$で計算するので、それほど無理なものでもないと思います)。
そうすると拡張カルマンフィルタの状態更新の手法が、そのままRNNの状態、つまり重みの更新に適用できます。状態更新の計算式はかなりややこしいので詳細は省きますが、こうして拡張カルマンフィルタの手法をRNNに持ち込むのがEKFという手法です。
計算を簡略化するための方法もあり有望な手法ですが、BPTTやRTRL同様、精度を出すには経験に基づくチューニング(learning rate,ネットワークの構成など)が必要です。
RNNのライブラリ
メジャーどころのライブラリで明確に対応しているのはpybrainです。Recurrent Networkのチュートリアルも用意されています。
Deep Learningで有名なpylearn2でも可能なようですが、パスを見て分かるとおり現時点(2015/1)ではまだsandboxの中にあり、実際使うには不安な状態です。
lisa-lab/pylearn2 pylearn2/pylearn2/sandbox/rnn/models/tests/test_rnn.py
自前で実装する際は、Theanoを使った方法が紹介されています。
Implementing a recurrent neural network in python
gwtaylor/theano-rnn
こちらはRNNとRBMを組み合わせたものになりますが、コードも含め実装が紹介されています。
Modeling and generating sequences of polyphonic music with the RNN-RBM
RNN-RBMによる旋律の予測と生成と音楽情報処理に関する紹介
その他、neuraltalkは画像とそれに対する説明を学習させ、画像を与えるとそれに対する説明を出力すといったモデルのようです。構築のためのライブラリというよりはできあいのものになりますが、この用途で使うのならばよいと思います。
RNNの実装
今回は、上記のとおり実装例もあるpybrainを利用してRNNを実装してみます。
PyBrainの最新版は0.3.3です(2015/1時点)。PYPIサイトにアップはされている・・・ようですがpipから入るのは0.3.2であるため、git cloneでリポジトリを落としてきてインストールします。手順・依存ライブラリはこちらをご参照ください。
メインな依存はScipyです。Pythonは2.5と書いてありますが、手元の環境でPython3.4.2でテスト(python runtests.py)が通ることを確認済みです。Issueなどを見るとPython3は未対応の部分もある気配がしますが、使っている中で問題になったところはありませんでした(知らずに誤差が出てたりしなければ・・・)。
予測する時系列のデータは、ボールの軌道のデータを生成して使用しました。最初はこちらの論文で使用されていたボールのバウンドデータ (www.cs.utoronto.ca/~ilya/code/2008/RTRBM.tar) を使おうと思ったのですが、動作環境がPython2と古かったうえ、READMEの記述を信じるなら学習に1週間かかる(引用:the bouncing balls problems trains for a considerably longer amount of time (about a week on a fast computer...))とのことだったので、単純な軌道を生成して使うことにしました。
モデルの構築についてはPyBrainのチュートリアルに丁寧に書かれていますが、主要な記述方法について以下にまとめておきます。
Welcome to PyBrain’s documentation!
ネットワークの構築
pybrain.structureを利用して組み立てを行います。下記では、2-3-1でバイアス項を持つ通常のネットワークを構築しています。
Building Networks with Modules and Connections
from pybrain.structure import FeedForwardNetwork, LinearLayer, SigmoidLayer, BiasUnit, FullConnection
net = FeedForwardNetwork()
net.addInputModule(LinearLayer(2, name='i'))
net.addModule(BiasUnit('bias'))
net.addModule(SigmoidLayer(3, name='h'))
net.addOutputModule(LinearLayer(1, name='o'))
# connect nodes
net.addConnection(FullConnection(net['i'], net['h']))
net.addConnection(FullConnection(net['bias'], net['h']))
net.addConnection(FullConnection(net['bias'], net['o']))
net.addConnection(FullConnection(net['h'], net['o']))
buildNetworkを使うとより簡単に構築できます。下記は上記の処理と同じです。
net = buildNetwork(2, 3, 1, bias=True, hiddenclass=SigmoidLayer)
ネットワークの学習
学習を行うために、まずはデータセットを用意します。下記では、上記で構築したネットワークに合わせて入力2に対し出力1のデータをaddSampleで渡しています(なお、ドキュメント中に出てくるappendLinkedとaddSampleは等価です)。
from pybrain.datasets import SupervisedDataSet
ds = SupervisedDataSet(2, 1)
ds.addSample((0, 0), (0,))
...
用意したデータセットで、学習を行います。trainer.trainはdouble proportional to the error(二乗誤差?)を返却するので、これでトレーニングデータへの当てはまりを評価することができます。
Training your Network on your Dataset
from pybrain.supervised.trainers import BackpropTrainer
net = buildNetwork(2, 3, 1, bias=True, hiddenclass=TanhLayer)
trainer = BackpropTrainer(net, ds)
err = trainer.train()
ネットワークによる予測
予測はactivate関数で行います。
net.activate([1, 2])
RNNの構築
RNNの場合も、通常のネットワーク構築とほぼ変わりません。
RNNではRecurrentNetworkを使用し、再帰のつながりを行う際は、addRecurrentConnectionにより接続を行います。
そして、予測はnet.reset()でいったんリセットを行った後にactivateで実行します。
activateについては、上記の例ではずっと同じ値を入れて予測していましたが実際は予測した値を再度入れて~とやらないと当てはまりが悪かったです(理論上は最初の一つの入力さえあればその後どんどん予測できるので初期値のままでも問題ない気もしますが・・・)。
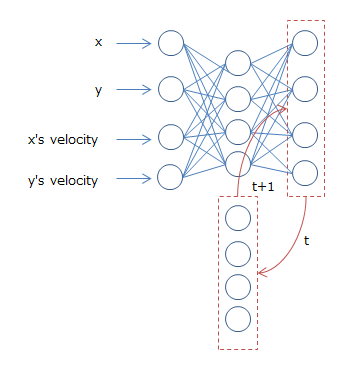
今回はElmanとJordanの二つで試してみました。下記は、Jordanでのイメージです。x,yの座標とそれぞれの加速度を入力として渡しています。
加速度は時刻tの位置と時刻t+1の位置で決まるため隠れ層でうまく学習してくれる・・・と思ったのですが、どうにも精度が出なかったので入力パラメーターとして加えました。
学習データは、同じ初期加速度の下初期位置を変えて幾つかバッチを用意し、それで学習/テストを行いました。
初期加速度は学習/テストデータで同じため、このモデルはその加速度の下、ある地点にボールが置かれたときその後どのような軌跡を描くかを推測するモデルになっています。
気になる精度ですが・・・テストデータとの誤差は平均5.7程度と、あまりよくありませんでした。
今回のデータは10×10の正方形の中でバウンドするボールの軌道を予測するもののため、誤差が5.7ということは予測はほぼ完全に外れているといっていいレベルです。
アニメーションでみるとまあ気持ちはわかる程度に動いてはいるのですが、完全再現には程多いものになっています。
隠れ層・ノードの増減も試してみましたが変わらず・・・といった感じでした。
検証に使用したコードはこちらになっています。もし我こそはという方がいたらPull Requestをお待ちしております。
参考
- RNNについて
- Recurrent neural network
- Types of artificial neural networks
- Hopfield network
- Echo state network
- What is the difference between Elman and Jordan neural networks
- Recurrent Neural Networks
- Bidirectional recurrent neural networks
- A tutorial on training recurrent neural networks, covering BPPT, RTRL, EKF and the "echo state network" approach
- A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm
- RNNの実装に関する論文など
- Modeling and generating sequences of polyphonic music with the RNN-RBM
- Modeling Temporal Dependencies in High-Dimensional Sequences:Application to Polyphonic Music Generation and Transcription
- ↑論文を日本語で解説してくださっている記事 RNN-RBMによる旋律の予測と生成と音楽情報処理に関する紹介
- Continuous time recurrent neural networks for grammatical induction
- PyBrainについて
- Welcome to PyBrain’s documentation!