目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
| リンク | 説明 |
|---|---|
| marubatsu.py | Marubatsu、Marubatsu_GUI クラスの定義 |
| ai.py | AI に関する関数 |
| test.py | テストに関する関数 |
| util.py | ユーティリティ関数の定義 |
| tree.py | ゲーム木に関する Node、Mbtree クラスなどの定義 |
| gui.py | GUI に関する処理を行う基底クラスとなる GUI クラスの定義 |
AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。
その他の αβ 法の効率を改善するアルゴリズム
これまでに αβ 法の効率を改善 するアルゴリズムとして null window search を利用した スカウト法 と MTD(f) 法 を紹介しました。今回の記事では他の αβ 法の効率を改善するためのアルゴリズムをいくつか紹介します。ただし、それらのアルゴリズムの実装は行わないので、興味がある方は実際に実装してみて下さい。
また、他にも様々なアルゴリズムが考案されているので興味がある方は調べてみて下さい。参考までに Chess Programming wiki の αβ 法の記事のリンクを下記に紹介します。
また、1999 年に発表された論文なのでかなり古いですが、ゲーム木の探索のトレンドをまとめた論文のリンクを下記に紹介します。下記の論文で行なわれた検証では MTD(f) 法はスカウト法よりも 1 ~ 15 % 程効率が高かったそうです。
SSS* と Dual*
SSS*1と Dual*2 は MTD(f) 法より前に考案 されたアルゴリズムですが、アルゴリズムが複雑で理解しづらい点と、枝狩りの効率化を行うために必要となる処理の効率があまり高くなく、総合的に見るとあまり効率が良くない 点から、MTD(f) として作り直された ようです3。正直に言うと、筆者もこれらのアルゴリズムについてはちゃんと理解していません。参考までに Chess Programming wiki の該当する記事のリンクを下記に紹介します。
MTD(∞) 法
以前の記事で説明したように、MTD(f) 法の MTD は Memory-enhanced Test Driver の略で、ミニマックス値が指定した値よりも 大きいかどうかのテスト(判定)の処理の効率を 置換表を利用 して高めた アルゴリズムのこと を表します。従って、MTD(f) 法以外 の MTD に分類される アルゴリズムがあります。
MTD(∞) 法は MTD(f) 法と似ていますが、ミニマックス値を推定せず に 最初に常に f を正の無限大として計算 する手法です。null window search を行うたびに f が ∞ からミニマックス値に向かって減っていくことでミニマックス値が求められますが、null window search の回数 が MTD(f) 法と比べて 多くなる可能性が高い ため、精度の高いミニマックス値を推定することができる場合は MTD(f) 法の方が効率が高くなります。そのためこのアルゴリズムが実際に使われることはほとんどないと思います。
同様に最初のf を常に負の無限大や 0 としてミニマックス値を計算すると、おそらく MTD(―∞) 法や MTD(0) 法となるのではないかと思います。
C* と Nega C*
C* は 二分法 でミニマックス値を 効率よく計算 するアルゴリズムです。Nega C* は C* と同様ですが min ノードの評価値の正負を反転させることで処理をまとめたアルゴリズムです。
参考までに Chess Programming wiki の該当する記事のリンクを下記に紹介します。
二分法とは何か
二分法(bisection method)は 何かを探索 する際に、「全体を半分にわけて その どちらに 探索したいものが 含まれているかを探す」という処理を 繰り返す というアルゴリズムです。探索したいものが 2 つの集合のどちらに含まれているかを効率よく判定できる場合 に、効率が良い探索のアルゴリズム として様々な場面で 実際に良く使われます。
具体的な使用例としては、二分法で 辞書から単語を探す のがわかりやすいでしょう。辞書は 単語が アルファベット順やあいうえお順などの 順番の並べられている ので、特定のページを開いた時に 調べたい単語がそのページよりも前にあるか どうかを 効率よく判定 することができます。辞書から単語を二分法で探索する具体的なアルゴリズムは以下の通りです。
- 辞書のちょうど 真ん中のページを開く。二分法の 名前 は、この作業によって辞書のページが 同じページ数 の 2 つの集合に二分される ことが 由来である
- 開いたページの 先頭の単語を見る ことで、調べたい単語が 開いたページより前にあるかどうか を判定し、調べたい単語が 含まれていないほう を 検索の対象から取り除く。この作業によって検索の対象となる ページの数が半分 になる
- 辞書のページが 1 ページになるまで手順 1、2 を繰り返し、1 ページになったら そのページから単語を探す
二分法では、手順 1、2 の処理を行うたびに 探索範囲を半分にする ことができるので、$\boldsymbol{n}$ 回の探索 を行うことで 探索範囲 を $\boldsymbol{2^n}$ 分の 1 に減らす ことができます。たとえば $\boldsymbol{2^{10} = 1024}$ なので、手順 1、2 の処理を 10 回行う ことで 1000 ページの辞書 の中から 必ず目的の単語が入ったページを検索 することができます。$\boldsymbol{2^{20} = 約 100 万}$ なので、二分法を使えば たった 20 回以下 の手順 1、2 の処理で 100 万ページ の辞書の中から単語を検索することができます。このように二分法は効率が良いので実際に良く使われます。
探索したいものが 2 つの集合のどちらに含まれているかを 効率よく判定できない場合 は 二分法を利用することはできません。例えば本の中から特定の単語を探すには、索引などのヒントがなければ最初のページから順番に探すしかないでしょう。
一般的に、二分法行うためには、辞書のように単語を順番に並べ替える(ソート)などの、事前の作業を行う必要があります。コンピューターでは、ソート済みのデータに対して二分法を利用した探索のアルゴリズムの事を 二分探索 と呼びます。ソート済のデータを作成する際に 二分木 という 木構造のデータ が良く使われます。
参考までに二分法、二分探索、二分木の Wikipedia のリンクを下記に紹介します。
C* のアルゴリズム
null window search を利用することで ミニマックス値が特定の値以上であるか どうかを 効率よく判定 することができます。C* は null window search を利用することで 二分法による探索 を行うことができます。
null window search は確かに効率が良いのですが、先程の辞書の例ほど効率よくミニマックス値が特定の値以上であるかどうかを判定することはできないので null window search を一定以上の回数行うと、通常のウィンドウ幅の αβ 法で αβ 値を計算するよりも効率が悪くなります。そのため C* の効率が常に αβ 法よりも良くなるとは限りません。ミニマックス値の推定の精度が悪い場合に MTD(f) 法の効率が αβ 法より悪くなる場合があるのも同様の理由です。
C* のアルゴリズム は以下の通りです。なお、無限大が含まれた数値の平均 を 計算することはできない ので、C* では最初の ミニマックス値の範囲の下界と上界 を無限大ではない、有限の値に設定する必要 があります。
- ミニマックス値の下界と上界 を、ミニマックス値の範囲を含む 何らかの 有限の値に設定する
-
下界と上界が等しくなるまで 下記の処理を 繰り返す
- $\boldsymbol{α}$ = (下界 + 上界) / 2 を計算し、($\boldsymbol{α}$, $\boldsymbol{α + 1}$) を ウィンドウ とする null window search で αβ 値を計算 する。ただし、$α$ が整数でない場合は切り捨てるものとする
- αβ 値 $\boldsymbol{> α}$ の場合は fail high なのでミニマックス値は αβ 値 以上 である。従って 下界を αβ 値 で更新 する。そうでなければ fail low なのでミニマックス値は αβ 値以下 である。従って 上界を αβ 値 で更新 する
MTD という名前はついていませんが、C* は MTD(f) 法と同様に同じノードに対して null window search を複数回行うので、置換表を利用したほうが良い でしょう。
C* のアルゴリズムは 厳密には二分法ではありません。その理由は null window search ではミニマックス値が特定の値以上であるか 以上の厳密な判定 を行うことができ、C* ではその性質を利用しているから です。
具体的には ($\boldsymbol{α}$, $\boldsymbol{α + 1}$) というウィンドウで null window search を行なった結果、αβ 値として $\boldsymbol{α}$ 未満の値が計算 された場合は、ミニマックス値の範囲として $\boldsymbol{α}$ 以下よりも厳密 な αβ 値以下である ことが判定できます。同様に αβ 値として $\boldsymbol{α+1}$ より大きな値が計算 された場合は、ミニマックス値の範囲として $\boldsymbol{α+1}$ 以上よりも厳密 な αβ 値以上である ことが判定できます。
下記は 厳密な二分法 で計算するように C* のアルゴリズムを修正したものです。修正した部分を太字にしました。
- ミニマックス値の下界と上界を、ミニマックス値の範囲を含むような何らかの有限の値に設定する
- 下界と上界が等しくなるまで下記の処理を繰り返す
- $α$ = (下界 + 上界) / 2 を計算し、($α$, $α + 1$) を ウィンドウとする null window search で αβ 値を計算する。ただし、$α$ が整数でない場合は切り捨てるものとする
- αβ 値 > $α$ の場合は fail high なのでミニマックス値は $\boldsymbol{α + 1}$ 以上 である。従って、下界を $\boldsymbol{α + 1}$ で更新する。そうでなければ fail low なのでミニマックス値は $\boldsymbol{α}$ 以下 である。従って、上界を $\boldsymbol{α}$ で更新する
C* で更新される ミニマックス値の範囲 は、αβ 値 が $\boldsymbol{α}$ または $\boldsymbol{α + 1}$ の場合 は 二分法と変わりません が、それ以外の場合 は二分法よりも 狭くなります。従って、C* は二分法以上の効率 で計算を行うことができます。
C* と MTD(f) 法の効率の比較
C* のアルゴリズム は MTD(f) 法と同様に、ミニマックス値の範囲 を null window search の結果によって 狭めていく というものです。C* が二分法を使って null window search のたびに ミニマックス値の範囲を半分以下に減らす のに対し、MTD(f) 法 は null window search のたびに f と新しく計算した αβ 値の差だけしか ミニマックス値の 範囲が減りません。そのため一見すると C* の方が MTD(f) 法よりも効率が高いように思えるかもしれませんが、精度の高いミニマックス値を推定できる場合 は MTD(f) のほうが効率が高くなる傾向 があります。
このことをわかりやすく説明するために、具体例として ミニマックス値の範囲の初期値 を [-1000, 1000]、ミニマックス値を 30 とした場合に C* と MTD(f) 法で行なわれる計算を比較します。
まず、C* で行なわれる計算 を下記の表で示します。C* は先程のノートで説明したように 最悪の場合は二分法と同じ効率になる ので、以下の計算では null window search の計算結果である αβ 値として、fail low の場合は $\boldsymbol{α}$ が、fail high の場合は $\boldsymbol{α + 1}$ が計算されたものとします。下記の表から 最悪の場合でも C* では 11 回の null window search でミニマックス値を計算できることがわかります。
| 回数 | ウィンドウ | αβ 値 | αβ 値の範囲 | 更新後のミニマックス値の範囲 |
|---|---|---|---|---|
| 1 | (0, 1) | 1 | fail high | [1, 1000] |
| 2 | (500, 501) | 500 | fail low | [1, 500] |
| 3 | (250, 251) | 250 | fail low | [1, 250] |
| 4 | (125, 126) | 125 | fail low | [1, 125] |
| 5 | (63, 64) | 63 | fail low | [1, 63] |
| 6 | (32, 33) | 32 | fail low | [1, 32] |
| 7 | (16, 17) | 17 | fail high | [17, 32] |
| 8 | (24, 25) | 25 | fail high | [25, 32] |
| 9 | (28, 29) | 29 | fail high | [29, 32] |
| 10 | (30, 31) | 30 | fail low | [29, 30] |
| 11 | (29, 30) | 30 | fail high | [30, 30] |
$α$ = (下界 + 上界) / 2 の切り捨てとしたのは、切り上げで計算すると 上記の 11 回目の計算でウィンドウが (30, 31)、αβ 値が 30 で fail low のように 10 回目と同じ結果になる ため、ミニマックス値の範囲 が [29, 30] のまま 変化しなくなるから です。
MTD(f) 法 では以前の記事で説明したように、null window search の回数と、ミニマックス値の推定値である $f$、ミニマックス値である $s$ の間には下記の表のような関係があります。
| 条件 | 最小回数 | 最大回数 |
|---|---|---|
| $\boldsymbol{f < s}$ | $2$ | $s - f + 2$ |
| $\boldsymbol{f = s}$ | $2$ | $2$ |
| $\boldsymbol{f > s}$ | $2$ | $f - s + 1$ |
従って、ミニマックス値の推定値 として 22 を推定 した場合は 最大で $30 - 22 + 2 = \boldsymbol{10}$ 回、39 を推定 した場合は最大で $39 - 30 + 1 =\boldsymbol{10}$ 回 の null window search が計算されるので、22 ~ 39 の範囲 のミニマックス値を 推定する と MTD(f) 法の方が C* よりも 最悪の場合に効率が高く なります。
このことを 辞書で単語を探す場合に例えて説明 すると以下のようになります。
1000 ページの英語の辞書 の中から 30 ページ目に記載 されている apple という単語を 二分法で探す のは、先程の C* の表の 2 回目から探索を行った場合と同じ と考えることができるため 10 回 ページを開く必要があります。
一方、MTD(f) と同様の考え方 で単語を探す場合は、apple という単語が 明らかに辞書の先頭のほうにある ことから apple が 載っていそうなページ として 先頭のほうにあるページ を開き、そこから 1 ページずつ単語を探す という方法をとります。例えば apple が載っていそうなページとして 開いたページが 30 ページ目 の場合は、ページを開く回数 は $30 - 25 + 1 = \boldsymbol{6}$ 回ですみます。このように、単語が載っている ページの推定の精度が高ければ、二分法よりも 推定したページから順番に探す方が速く見つける ことができます。
精度の高いミニマックス値を推定できる場合 は MTD(f) のほうが効率が高くなる傾向 があるのは、このことによく似ています。
本記事ではまだ説明していませんが、反復深化 という手法を用いることで 精度の高いミニマックス値を推定することができる ので、一般的には C* はほとんど使われていない のではないかと思います。
Aspiration Windows
MTD(f) 法で行う null window search では、αβ 値が exact value の範囲になることはない ので、必ず 2 回以上 の null window search を行う必要があります。
Aspiration Windows では、推定したミニマックス値を含む ような 狭いウィンドウ幅 で αβ 値の計算を行ないます。そのため、推定したミニマックス値が正しければ、1 回の狭いウィンドウ幅 での αβ 値の計算によってミニマックス値を計算することができるため、MTD(f) 法よりも効率が高くなることが期待 できます。
ただし、ミニマックス値の 推定値を間違えた場合 でウィンドウの範囲内にミニマックス値が入らない場合は 2 回以上 の αβ 値の計算が必要になります。また、その際の ウィンドウ幅 は null window search よりも広い ため、MTD(f) 法よりも効率が悪くなってしまう という問題があります。
上記から、Aspiration Windows を利用する場合は ウィンドウ幅を広げすぎると効率が悪くなる が、ウィンドウ幅を狭くしすぎる とミニマックス値がウィンドウの 範囲内に入らなくなる可能性が高くなる という問題があるため、適切なウィンドウ幅を決めるのが難しい という問題があります。また、MTD(f)法と同様に、ミニマックス値の推定値の精度が非常に重要 となります。
スカウト法や MTD(f) と比較して Aspiration Windows のほうが効率が良くなるかどうかについては、ゲーム木の性質や、ミニマックス値の推定値の精度に左右されます。
参考までに Chess Programming wiki の該当する記事のリンクを下記に紹介します。
探索の並列化
最近のコンピューターには 複数の CPU が搭載されている ので、探索の処理を 複数の CPU で手分けして 同時に行う ことで 処理時間を減らす という手法があります。このような、複数の処理を同時に行う処理 のことを 並列処理(parallel processing)と呼びます。並列処理は実際に効果的ですが、正しく行うためには気をつけなければならない点が数多くあるので、実装はそれほど簡単ではありません。また、残念ながら $n$ 個の CPU で並列処理を行っても処理時間が $1/n$ になることは通常はありません。
本記事では並列処理については今のところは扱う予定はありません。
参考までに Chess Programming wiki の該当する記事のリンクを下記に紹介します。
ヒューリスティックな探索
これまでの記事で紹介した ミニマックス法や αβ 法などでは、いずれも 正確なミニマックス値を計算 していましたが、ゲーム木の ノードの数が多くなる と計算に時間がかかりすぎるようになるため、正確なミニマックス値を計算できなくなります。そのような場合は ミニマックス値の近似値を計算 する ヒューリスティックな探索 を行います。ヒューリスティックな探索については次回以降の記事で紹介します。
αβ 法の最大効率の証明
以下の記事の証明は理解しなくても大きな問題はありません。数式がかなり出てくるので数学が苦手な方は飛ばしてもらっても構いません。
以前の記事で、αβ 法で 最も効率よく枝狩りを行なえる場合 は計算する必要があるノード数が 全体のノードの数の平方根の値くらいになる ということを説明しました。そのことは、以前の記事の 完璧な move ordering での検証を利用 することで証明することができます。
検証を行うゲーム木の性質と検証方法
あらゆるゲーム木での証明を行うことは非常に難しいので、深さが $\boldsymbol{d}$ で、リーフノード以外の すべてのノードに $\boldsymbol{n}$ 個の子ノード が存在するゲーム木の場合で説明します。
このようなゲーム木のことを バランス木(平衡木) と呼びます。
ただし、ルートノードの深さを 0、$\boldsymbol{n ≧ 2}$ とします。$n ≧ 2$ としたのは、すべてのノードの子ノードの数が 1 の場合は αβ 法で枝狩りが行われることはない ため、ミニマックス法と αβ 法の 効率が常に同じになる からです。
他の形状のゲーム木では平方根の値くらいになるとは限りません。例えば 〇× ゲームのゲーム木は深さが浅い程子ノードの数が多くなるのでこの性質を満たしません。
ミニマックス法 では すべてのノードの評価値を計算 します。また、αβ 法 で 最も効率よく枝狩りを行える のは 完璧な move ordering を行った場合です。そこで、下記を比較することで αβ 法の最大効率を計算することにします。
- ミニマックス法で計算されるノードの数
- 完璧な move ordering での αβ 法で計算されるノードの数
ミニマックス法で計算されるリーフノードの数
これまでの記事では、評価値を計算したすべてのノードの数 で効率を比較してきましたが、評価値を計算したリーフノードの数 で効率を比較するという方法も 良く使われます。本記事では 計算を簡単にするため、ミニマックス法と最大効率の αβ 法を、評価値が計算された リーフノードの数で比較 することにします。
計算がかなり面倒になりますが、ノードの総数で比較したい方は計算してみて下さい。その場合の結論はリーフノードで比較した場合と変わらないことが確認できると思います。
リーフノードの数で比較する理由
リーフノードの数で比較しても良い理由について説明します。
リーフノード以外のノードが $\boldsymbol{n}$ 個の子ノードを持つゲーム木 は、深さが 1 増えるたび に ノードの数が $\boldsymbol{n}$ 倍 になります。従って 深さが $\boldsymbol{i}$ のノードの数 は $\boldsymbol{n^i}$ となるため、深さが $d$ の リーフノードの数 は $\boldsymbol{n^d}$ となります。
深さが $\boldsymbol{d}$ のゲーム木の ノードの数の総数 は、深さが 0 ~ $\boldsymbol{d}$ までの ノードの数の合計 なので、以下の式で計算することができます。
$n^0 + n^1 + n^2 + ・・・ n^d$
数学では、このような式の中の 特定の数を増やしながら その 合計を計算する式 を Σ(ギリシャ文字のシグマの大文字)という記号を使って、下記のように 簡潔に記述 します。この記法は高校の数学で習うもので、良く使われます。
$\sum_{i=0}^{d}n^i$
この式に対して、下記の理由から $\boldsymbol{n^d ≦ \sum_{i=0}^{d}n^i < 2n^d}$ という 式が成り立ちます。これは、子ノードの数が $n$、深さが $d$ のバランス木の ノードの数の総数 が、リーフノードの数の倍以上にはならない ことを表します。ノードの数は深さが 1 つ増えるたびに $n$ 倍になるため、$\boldsymbol{n}$ や $\boldsymbol{d}$ が大きい場合 はノードの総数の代わりに リーフノードの数を使って比較を行っても結果はそれほど大きくかわりません。
$n^d ≦ \sum_{i=0}^{d}n^i < 2n^d$ が成り立つ理由は以下の通りです。
$n^d ≦ \sum_{i=0}^{d}n^i $ であることは、以下の式から明らかです。
$\sum_{i=0}^{d}n^i = n^0 + n^1 + ・・・ + n^d$
$\sum_{i=0}^{d}n^i$ は $n ≠ 1$ の場合は以下の式で計算することができます。その理由については次のノートで説明します。
$\sum_{i=0}^{d}n^i = \frac{n^{d+1} - 1}{n - 1}$
また、上記の式は下記のように書き直すことができます。
$\frac{n}{n - 1}n^d - \frac{1}{n - 1}$
$n ≧ 2$ の場合は $1 < \frac{n}{n - 1} ≦ 2$ なので、$\frac{n}{n - 1}n^d ≦ 2n^d$ です。
また、$n ≧ 2$ の場合は $0 < \frac{1}{n- 1} ≦ 1$ です。
上記から $\sum_{i=0}^{d}n^i = \frac{n}{n - 1}n^d - \frac{1}{n - 1} < \frac{n}{n - 1}n^d ≦ 2n^d$ となるので、$\sum_{i=0}^{d}n^i < 2n^d$ であることがわかります。
$n ≠ 1$ の場合に下記の式が成り立つ理由について説明します。
$\sum_{i=0}^{d}n^i = \frac{n^{d+1} - 1}{n - 1}$
$\sum_{i=0}^{d}n^i$ に $(n - 1)$ を乗算して式を展開すると下記のようになります。
$(\sum_{i=0}^{d}n^i)(n - 1) = (n^0 + n^1 + ・・・ + n^{d})(n - 1)$
$= (n^1 + n^2 + ・・・ + n^{d + 1}) - (n^0 + n^1 + ・・・ + n^{d})$
$= n^{d + 1} - n^0 = n^{d + 1} - 1$
上記の両辺を改めて $n - 1$ で割り算すると下記の先程の式が求められます。
$\sum_{i=0}^{d}n^i = \frac{n^{d+1} - 1}{n - 1}$
なお、数学では 0 で割り算を行うことはできないので、$n ≠ 1$ という条件が必要になります。
最大効率のアルファベータ法で計算されるリーフノードの数
αβ 法は精度が 100 % の move ordering を行なった際に効率が最大となります。
その場合に計算されるゲーム木のノードは 以前の記事 から下図のようになります。
① → ② → ① → ② の 繰り返しの図
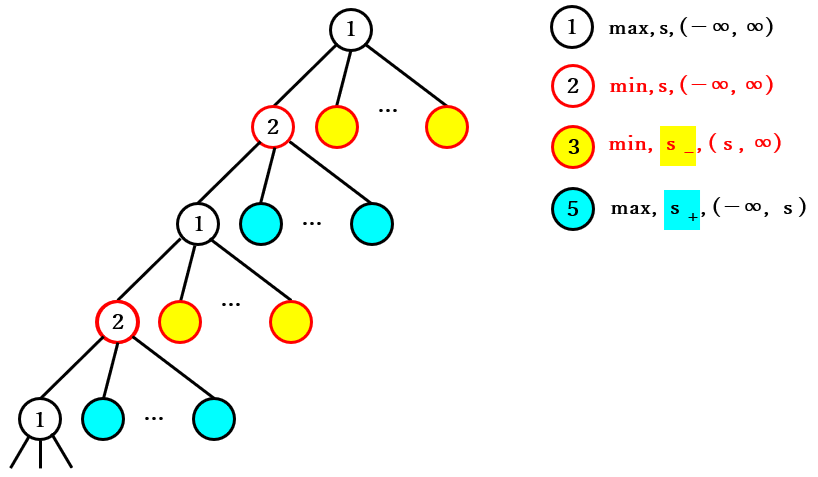
③ → ④ → ③ → ④ の繰り返しの図

⑤ → ⑥ → ⑤ → ⑥ の繰り返しの図
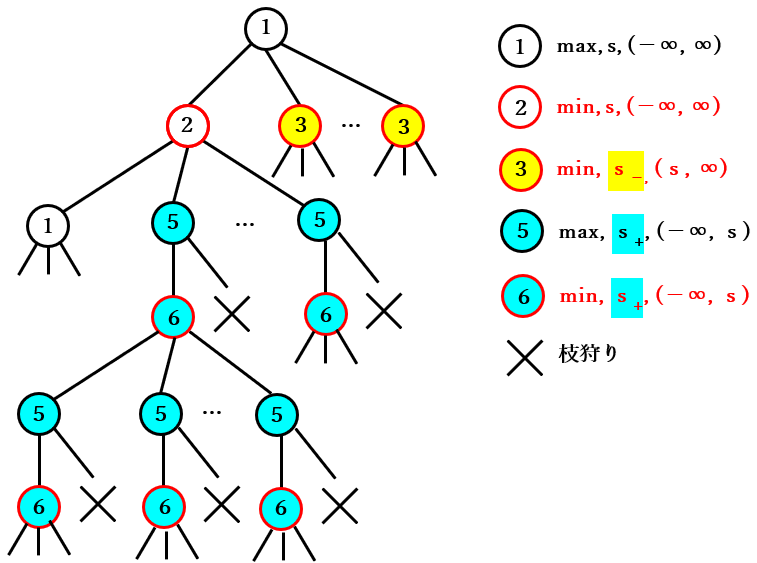
ルートノードが max ノードの場合のゲーム木の分割
ルートノードは max ノードと min の場合がありますが、どちらも同様の性質を持つ ので、ルートノードが max ノードの場合のみ説明を行います。
ルートノードが max ノード の場合のゲーム木は 下図の 2 種類の部分木に分割 できます。
- ルートノードの最初の子ノード(2 のノード)をルートノードとする部分木
- それ以外のノードを持つ部分木
表記を短くするために、ゲーム木全体を $T$、前者の部分木を $U$、後者の部分木を $V$ と表記し、$T$ が $U$ と $V$ の ノードで構成されること を $\boldsymbol{T=U+V}$ と表記することにします。

また、$\boldsymbol{T}$ のリーフノードの数 は、上記で分割した 2 つの部分木 $\boldsymbol{U}$ と $\boldsymbol{V}$ のリーフノードの合計 で計算されます。
V のリーフノードの数の計算
先に $\boldsymbol{V}$ の リーフノードの数 を計算することにします。
当然ですが、深さが 0 のルートノードの 数は 1 です。
深さが 1 のノードの数は、ルートノードの 最初のノードを除く必要がある ので、$\boldsymbol{n - 1}$ になります。
深さが 1 以降 のノードでは、下記の子ノードの計算が行われます。
- 深さが奇数 のノードでは、最初の子ノードのみが計算 される
- 深さが偶数 のノードでは、$\boldsymbol{n}$ 個のすべての子ノードが計算 される
従って、深さが 6 までのノードの数 は以下の表のようになります。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| $1$ | $n-1$ | $n-1$ | $(n - 1)×n$ | $(n - 1)×n$ | $(n - 1)×n×n$ | $(n - 1)×n×n$ |
上記の式の () を外し、式を $\boldsymbol{n}$ のべき乗で書き直す と以下の表のようになります。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| $1$ | $n^1-1$ | $n^1-1$ | $n^2 - n^1$ | $n^2 - n^1$ | $n^3 - n^2$ | $n^3 - n^2$ |
上記の表から深さ $i$ のノードの数は以下の式で計算できることがわかります。
- $i$ が 0 の場合は 1 となる
- $i$ が偶数の場合は $n^{\frac{i}{2}} - n^{\frac{i}{2}-1}$ となる
- $i$ が奇数の場合は $n^{\frac{i+1}{2}} - n^{\frac{i+1}{2}-1}$ となる
$V$ の深さ $i$ のノードの数は、ゲーム木の深さ $\boldsymbol{i}$ によって変化する ので、その数を $\boldsymbol{v(i)}$ という関数で表記することにします。
$V$ の深さ $i$ のノードの数を表す $\boldsymbol{v(i)}$ は下記の式で計算される。
- $i$ が 0 の場合は 1
- $i$ が偶数の場合は $n^{\frac{i}{2}} - n^{\frac{i}{2}-1}$
- $i$ が奇数の場合は $n^{\frac{i+1}{2}} - n^{\frac{i+1}{2}-1}$
リーフノードの深さは $d$ なので、$\boldsymbol{V}$ のリーフノードの数 は $\boldsymbol{v(d)}$ で計算できます。
U の性質の考察
$U$ は下図の 2 をルートノードとする部分木 ですが、よく見ると その構造 は 深さが $\boldsymbol{d - 1}$ である点を除くと $\boldsymbol{T}$ と全く同じ であることがわかります。そこで、$U$ を $\boldsymbol{T'}$ と表記 することにします。
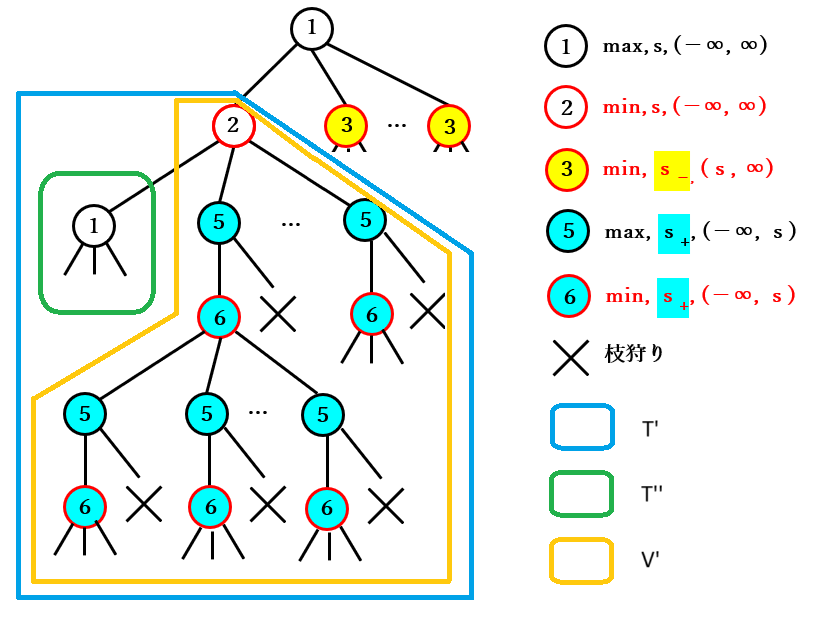
$T'$ は $T$ と同様に下記の 2 種類の部分木に分割することができます。
- $T'$ のルートノードの 最初の子ノード をルートノードとする部分木
- それ以外の $T'$ のノードを持つ部分木
前者を $T''$、後者を $V'$ と表記することにすると、$\boldsymbol{V'}$ は 深さが $\boldsymbol{d-1}$ である点を除けば、$\boldsymbol{V}$ と全く同じ構造 を持ちます。図は省略しますが、$\boldsymbol{T''}$ の構造 は深さが $\boldsymbol{d-2}$ である点を除けば $\boldsymbol{T}$ と同じ です。
T のリーフノードの数の計算式
上記から、深さが $\boldsymbol{i}$ の $T$、$V$ と 同じ構造を持つ部分木 をそれぞれ $T(i)$、$V(i)$ と表記すると、$i ≧ 2$ の場合に下記の式が成り立つことがわかります。
$T(i) = T(i - 1) + V(i)$
$\boldsymbol{T}$ は 深さが $\boldsymbol{d}$ のゲーム木 なので、$T$ は 下記の式 で表すことができることがわかります。
$T = T(d)$
$= T(d - 1) + V(d)$
$= T(d - 2) + V(d - 1) + V(d)$
$= T(d - 3) + V(d - 2) + V(d - 1) + V(d)$
$= ・・・$
$= T(0) + V(1) + V(2) + ・・・ + V(d)$
深さが 0 の木 はルートノードしか存在しないのでの $\boldsymbol{T(0)}$ のリーフノードの数は 1 です。また、深さが $\boldsymbol{d}$ の $\boldsymbol{V}$ のリーフノードの数は $\boldsymbol{v(d)}$ で計算できるので、$\boldsymbol{V(i)}$ のリーフノードの数 は $\boldsymbol{v(i)}$ で計算できます。$\boldsymbol{v(0) = 1}$ なので、$\boldsymbol{T}$ のリーフノードの数 は以下の式で計算できます。
$1 + v(1) + v(2) + ・・・ + v(d)$
$= v(0) + v(1) + v(2) + ・・・ + v(d)$
$=\sum_{i=0}^{d}v(i)$
$\boldsymbol{T}$ のリーフノードの数 は下記の式で計算できる。
$\boldsymbol{\sum_{i=0}^{d}v(i)}$
ただし、$v(i)$ は以下の式で計算する。
- $i$ が 0 の場合は 1
- $i$ が偶数の場合は $n^{\frac{i}{2}} - n^{\frac{i}{2}-1}$
- $i$ が奇数の場合は $n^{\frac{i+1}{2}} - n^{\frac{i+1}{2}-1}$
d が偶数の場合の T のリーフノードの数の計算
次に、上記の $T$ のリーフノードの数を計算する式の計算を行うことにします。
$v(i)$ が計算する式は $\boldsymbol{i}$ が偶数と奇数で異なる ので、上記の式を計算する際は $\boldsymbol{d}$ が 偶数の場合と奇数の場合で分けて考えたほうが良い でしょう。
そこで、$\boldsymbol{d}$ が偶数の場合 のリーフノードの数を 先に計算する ことにします。
同様の理由で、$\sum_{i=0}^{d}v(i)$ の合計を計算する際に $\boldsymbol{i}$ が偶数の場合と奇数の場合で分けて考えたほうが 計算が わかりやすくなります。
$\boldsymbol{i}$ が偶数の場合 の $T$ のリーフノードの数を計算する式は 下記の表の合計 になります。
| 0 | 2 | 4 | 6 | ・・・ | $\boldsymbol{d}$ |
|---|---|---|---|---|---|
| $1$ | $n^1-1$ | $n^2 - n^1$ | $n^3 - n^2$ | ・・・ | $n^{\frac{d}{2}} - n^{\frac{d}{2}-1}$ |
上記の表のそれぞれの 式の前後を入れ替える と以下のようになります。
| 0 | 2 | 4 | 6 | ・・・ | $\boldsymbol{d}$ |
|---|---|---|---|---|---|
| $1$ | $-1 + n^1$ | $-n^1 + n^2$ | $-n^2 + n^3$ | ・・・ | $-n^{\frac{d}{2}-1} + n^{\frac{d}{2}}$ |
これらの合計を計算すると、隣り合った数字が打ち消しあう ため、$\boldsymbol{n^{\frac{d}{2}}}$ だけが残ります。従って、$\boldsymbol{i}$ が偶数 の場合の 合計は $\boldsymbol{n^{\frac{d}{2}}}$ となります。
$\boldsymbol{i}$ が奇数 の場合は下記の表のようになります。なお、$\boldsymbol{i}$ が $\boldsymbol{d-1}$ の場合は $i$ が奇数の場合の $v(i) = n^{\frac{i+1}{2}} - n^{\frac{i+1}{2}-1}$ に $i = d - 1$ を代入することで以下のように計算しました。
$v(d-1) = n^{\frac{(d-1)+1}{2}} - n^{\frac{(d - 1)+1}{2}-1}$
$=n^{\frac{d}{2}} - n^{\frac{d}{2}-1}$
$=-n^{\frac{d}{2}-1} + n^{\frac{d}{2}}$
| 1 | 3 | 5 | ・・・ | $\boldsymbol{d-1}$ |
|---|---|---|---|---|
| $-1 + n^1$ | $-n^1 + n^2$ | $-n^2 + n^3$ | ・・・ | $-n^{\frac{d}{2}-1} + n^{\frac{d}{2}}$ |
上記の表のそれぞれの計算式は $i$ が 偶数の場合とほぼ同じ ですが、最初の 1 がない 点が 異なります。従って $\boldsymbol{i}$ が奇数 の場合の 合計は $\boldsymbol{n^{\frac{d}{2}}} - 1$ となります。
このことから、$\boldsymbol{d}$ が偶数の場合 の リーフノードの数 は $\boldsymbol{n^{\frac{d}{2}} + n^{\frac{d}{2}} - 1}$ となります。なお、$2n^{\frac{d}{2}} - 1$ のように まとめない理由はこの後で説明 します。
d が奇数の場合の T のリーフノードの数の計算
$\boldsymbol{d}$ が奇数の場合 は、最も深い偶数のノードの深さ は $\boldsymbol{d - 1}$ となります。従って $\boldsymbol{i}$ が偶数の場合 の合計は $d$ が偶数の場合の $\boldsymbol{n^{\frac{d}{2}}}$ の式の $d$ を$\boldsymbol{d-1}$ に置き換えた $\boldsymbol{n^{\frac{d-1}{2}}}$ となります。
最も深い奇数のノードの深さ は $\boldsymbol{d}$ なので、$\boldsymbol{i}$ が奇数の場合 の合計は$d$ が偶数の場合の $\boldsymbol{n^{\frac{d}{2}}} - 1$ の式の $d-1$ を$\boldsymbol{d}$ に置き換える ことで計算できます。$d-1$ を$d$ に置き換えるということは、$d$ を$\boldsymbol{d+1}$ に置き換える ということなので $\boldsymbol{n^{\frac{d+1}{2}} - 1}$ になります。
従って $\boldsymbol{d}$ が奇数の場合 の リーフノードの数 は $\boldsymbol{n^\frac{d-1}{2} + n^{\frac{d+1}{2}} - 1}$ となります。
T のリーフノードの数の計算式
上記をまとめると以下のようになります。
| $\boldsymbol{d}$ | リーフノードの数 |
|---|---|
| 偶数 | $n^{\frac{d}{2}} + n^{\frac{d}{2}} - 1$ |
| 奇数 | $n^\frac{d-1}{2} + n^{\frac{d+1}{2}} - 1$ |
$d$ が偶数の場合と奇数の場合で 式が異なるのはわかりづらい ので、1 つの式でまとめる ことにします。まとめる際には 数値 の 小数点以下での切り上げ と 切り下げ を行うので、それらを表す 数学の記号を紹介 します。
- $x$ の小数点以下の切り上げを $\lceil x \rceil$ と記述する。例えば $\lceil 2 \rceil = 2$、$\lceil 2.5 \rceil = 3$ である
- $x$ の小数点以下の切り下げ $\lfloor x \rfloor$ と記述する。例えば $\lfloor 2 \rfloor = 2$、$\lfloor 2.5 \rfloor = 3$ である
$\boldsymbol{d}$ が奇数の場合 は $\boldsymbol{\frac{d}{2}}$ を小数点以下で切り下げると $\boldsymbol{\frac{d-1}{2}}$ に、$\boldsymbol{\frac{d}{2}}$ を小数点以下で切り上げると $\boldsymbol{\frac{d+1}{2}}$ になります。従って $d$ が奇数の場合は以下の式が成り立ちます。
$n^\frac{d-1}{2} + n^{\frac{d+1}{2}} - 1 = n^{\lfloor \frac{d}{2} \rfloor} + n^{\lceil \frac{d}{2} \rceil} - 1$
例えば $d$ が 5 の場合 は以下の表のようになり、上記の式で正しく計算できる ことが確認できます。
| $\boldsymbol{d}$ | $\boldsymbol{\frac{d}{2}}$ | $\boldsymbol{\lfloor \frac{d}{2} \rfloor}$ | $\boldsymbol{\frac{d-1}{2}}$ | $\boldsymbol{\lceil \frac{d}{2} \rceil}$ | $\boldsymbol{\frac{d+1}{2}}$ |
|---|---|---|---|---|---|
| 5 | 2.5 | 2 | 2 | 3 | 3 |
一方、$\boldsymbol{d}$ が偶数の場合 は $\boldsymbol{\frac{d}{2}}$ は常に整数になる ので $\frac{d}{2}$ を 切り上げても切り下げても その 値は変わりません。従って、$d$ が奇数の場合は以下の式が成り立ちます。
$n^\frac{d}{2} + n^{\frac{d}{2}} - 1 = n^{\lfloor \frac{d}{2} \rfloor} + n^{\lceil \frac{d}{2} \rceil} - 1$
例えば $d$ が 6 の場合 は以下の表のようになり、上記の式で正しく計算できる ことが確認できます。
| $\boldsymbol{d}$ | $\boldsymbol{\frac{d}{2}}$ | $\boldsymbol{\lfloor \frac{d}{2} \rfloor}$ | $\boldsymbol{\lceil \frac{d}{2} \rceil}$ |
|---|---|---|---|
| 6 | 3 | 3 | 3 |
上記から下記の事がわかります。
$d$ が偶数でも奇数でも $T$ の リーフノードの数 は 下記の 1 つの式で表される。
$n^{\lfloor \frac{d}{2} \rfloor} + n^{\lceil \frac{d}{2} \rceil} - 1$
効率の比較
ミニマックス法 の場合のリーフノードの数と、最大効率の αβ 法 の リーフノードの数 を 表す式 は以下の表のようになります。
| 計算式 | |
|---|---|
| ミニマックス法 | $n^d$ |
| 最大効率の αβ 法 | $n^{\lfloor \frac{d}{2} \rfloor} + n^{\lceil \frac{d}{2} \rceil} - 1$ |
$\boldsymbol{n}$ と $\boldsymbol{d}$ が ある程度以上大きい場合 は、$\boldsymbol{n^{\lfloor \frac{d}{2} \rfloor} + n^{\lceil \frac{d}{2} \rceil}}$ の値が 1 を無視しても良い程に大きくなる ので、最大効率の αβ 法の計算式 の -1 を無視することができます。例えば $n=10$、$d=10$ の場合は下記の表のようにリーフノードの数が計算されるので、$n^{\lfloor \frac{d}{2} \rfloor} + n^{\lceil \frac{d}{2} \rceil}$ で計算して比較しても 結果にほとんど影響を与えません。
| リーフノードの数 | |
|---|---|
| ミニマックス法($n^d$) | 10,000,000,000 |
| 最大効率の αβ 法($n^{\lfloor \frac{d}{2} \rfloor} + n^{\lceil \frac{d}{2} \rceil} - 1$ で計算) | 199,999 |
| 最大効率の αβ 法($n^{\lfloor \frac{d}{2} \rfloor} + n^{\lceil \frac{d}{2} \rceil}$ で計算) | 200,000 |
$\boldsymbol{d}$ が偶数の場合 は $\boldsymbol{\lfloor \frac{d}{2} \rfloor = \lceil \frac{d}{2} \rceil = \frac{d}{2}} $ なので、$\boldsymbol{n^{\lfloor \frac{d}{2} \rfloor} + n^{\lceil \frac{d}{2} \rceil} = 2n^\frac{d}{2}}$ です。また、$\boldsymbol{n^d}$ の平方根 である $\boldsymbol{\sqrt{n^d} = n^{\frac{d}{2}}}$ です。従って、$\boldsymbol{d}$ が偶数の場合 は最大効率の αβ 法のリーフノードの数は、ミニマックス法のリーフノードの数の 平方根のほぼ 2 倍 になることがわかります。
$\boldsymbol{d}$ が奇数 の場合は $\boldsymbol{\lfloor \frac{d}{2} \rfloor = \frac{d-1}{2}}$、$\boldsymbol{\lceil \frac{d}{2} \rceil = \frac{d+1}{2}}$ なので以下の式が成り立ちます。
$n^{\lfloor \frac{d}{2} \rfloor} + n^{\lceil \frac{d}{2} \rceil} = n^{\frac{d-1}{2}} + n^{\frac{d+1}{2}}$
$= n^\frac{d}{2}(n^{\frac{-1}{2}} + n^{\frac{1}{2}})$
$= n^\frac{d}{2}(\frac{1}{\sqrt{n}} + \sqrt{n})$
従って、$\boldsymbol{d}$ が奇数の場合 は最大効率の αβ 法のリーフノードの数は、ミニマックス法のリーフノードの数の 平方根の $\frac{1}{\sqrt{n}} + \sqrt{n}$ 倍 になることがわかります。
$n$ が 2、5、10、100 の場合は、$\sqrt{n}$ と $\frac{1}{\sqrt{n}} + \sqrt{n}$ は以下の表のようになり、
$n$ が大きくなるにつれその違いはほとんどなくなります。
| n | $\sqrt{n}$ | $\frac{1}{\sqrt{n}} + \sqrt{n}$ |
|---|---|---|
| 2 | 1.41 | 2.12 |
| 3 | 1.73 | 2.31 |
| 5 | 2.24 | 2.68 |
| 10 | 3.16 | 3.48 |
| 100 | 10.00 | 10.10 |
| 1000 | 31.62 | 31.65 |
従って、$d$ が奇数の場合は最大効率の αβ 法のリーフノードの数は、ミニマックス法のリーフノードの数の 平方根のほぼ $\sqrt{n}$ 倍 になることがわかります。
上記をまとめると以下のようになります。
最大効率の αβ 法のリーフノードの数の、ミニマックス法のリーフノードの数の 平方根に対する比率 は下記のようになる。
- 深さ $d$ が偶数の場合は 約 2 になる
- 深さ $d$ が奇数の場合は 約 $\sqrt{n}$ になる
従って $\boldsymbol{n}$ を定数と考える と、最大効率の αβ 法のリーフノードの数は、ミニマックス法のリーフノードの数の 平方根に比例する。
先程示したようにバランス木の 全ノードの数 は リーフノードの数の 2 倍以下 なので、全ノードの数 で比較しても最大効率の αβ 法のノードの数がミニマックス法のノードの数の 平方根に比例する ことに変わりはありません。
別の見方 をすると、最大効率の αβ 法 では、同じ数のノードの評価値を計算することで、ミニマックス法のほぼ倍の深さ のゲーム木を 探索できる ということです。
証明方法は異なりますが、An analysis of alpha-beta pruning という論文でバランス木での αβ 法の最大効率がミニマックス法の平方根に比例することが証明されているので参考までにそのリンクを紹介します(論文の閲覧は有料です)。
今回の記事のまとめ
今回の記事では他の αβ 法を改善するアルゴリズムをいくつか紹介しました。また、バランス木 では最大効率の αβ 法の効率がミニマックス法の効率の 平方根に比例する ことを示しました。
本記事で入力したプログラム
今回の記事で入力したプログラムはありません。
次回の記事
-
SSS は state space search の略で、* はスターと読みます。アルゴリズムの名前に * が付く由来は A* というアルゴリズムにあります。* の意味については A* の Wikipedia の記事 の「歴史」の項目を参照して下さい ↩
-
Dual とは数学の双対問題(dual problem)から付けられた名前で、Dual* は SSS* の双対問題です。双対問題の説明を行うと長くなるので、興味がある方は 双対問題の Wikipedia を参照して下さい ↩
-
Chess Programming wikiでは、次のように説明されていました。"However, it turned out the algorithmic overhead was too big to pay off the saved nodes. Aske Plaat, Jonathan Schaeffer, Wim Pijls and Arie de Bruin pointed out, that SSS* can be reformulated as a sequence of alpha-beta null window calls with a Transposition Table. " ↩