Pythonで〇×ゲームのAIを一から作成する　その168　MTD(f) 法の仕組みと実装

Last updated at 2025-05-08Posted at 2025-05-04

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

util.py の説明に「現在は gui_play のみ定義されている」という間違いが説明されていたので修正しました。なお、過去の記事に遡って修正するのは大変すぎるので、そのままにしています。

リンク	説明
marubatsu.py	Marubatsu、Marubatsu_GUI クラスの定義
ai.py	AI に関する関数
test.py	テストに関する関数
util.py	ユーティリティ関数の定義
tree.py	ゲーム木に関する Node、Mbtree クラスなどの定義
gui.py	GUI に関する処理を行う基底クラスとなる GUI クラスの定義

AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。

MTD(f) 法

今回の記事では null window search を利用した、スカウト法よりも効率が高い と言われている MTD(f) 法 というアルゴリズムを紹介します。

利用する記号

今回の記事では下記の記号を利用します。なお、以前の記事で ミニマックス法 で求めることができる 正確な評価値 を ミニマックス値、αβ 法 で計算したミニマックス値の 範囲を表す可能性がある評価値 の事を αβ 値 のように区別して表記すると説明しましたが、最近の記事ではそのことを忘れて αβ 値のことを評価値と記述していたようです。わかりづらいので改めて αβ 値という用語を利用したいと思います（余裕があれば過去の記事も修正したいと思います）。

記号	意味
$\boldsymbol{N}$	MTD(f) 法でミニマックス値を計算するノード
$\boldsymbol{α}$	$N$ の αβ 値を計算する際の α 値の初期値
$\boldsymbol{β}$	$N$ の αβ 値を計算する際の β 値の初期値
($\boldsymbol{α}$, $\boldsymbol{β}$)	$N$ の αβ 値を計算する際のウィンドウ
[下界, 上界]	$N$ のミニマックス値の範囲

以前の記事のノートで説明したように、数学では [1, 2] は 1 以上 2 以下のように、端を含む範囲を [] の記号で囲って表記します。

MTD(f) 法の特徴

MTD(f) は Memory-enhanced Test Driver with node n and value f の略で、以下のような特徴を持ちます。

αβ 法やスカウト法と異なり、null window search のみ で ミニマックス値を計算 する
move ordering を行わない かわりに¹$\boldsymbol{N}$ のミニマックス値を推定 してから計算を行う
置換表の利用を前提 とする

このアルゴリズムで効率が高くなる理由については後で説明します。

MTD(f) は MT を利用したアルゴリズムの一つで、MT という名前は An Algorithm Faster than NegaScout and SSS* in Practice という論文で以下のような理由から命名されたようです。

null window search などによってミニマックス値が特定の値よりも大きいかどうかを判定することをテスト（test）と呼びます。また、置換表が過去の結果を記録（memory）することから、置換表によって効率を高めた（enhance）テストのことを MT(memory enhanced test)と命名したとのことです。

MTD(f) はノード n のミニマックス値を f と推定して MT を行うアルゴリズムなのでそのように命名されたようです。なお、MTD の D はドライバ（driver）の略で、コンピューターでは何かを動作させるシステムのことドライバと呼びます。

参考までに MTD(f) 法の Wikipedia、Chess Programming wiki、論文のリンクを示します。

MTD(f) 法の考え方とアルゴリズム

MTD(f) は以下のような考え方で null window search を複数回行う ことで $N$ のミニマックス値を計算する手法です。ただし、評価値として整数のみが計算 されるものとします。

最初はミニマックス値は不明 なので、ミニマックス値の範囲 を [$\boldsymbol{-∞}$, $\boldsymbol{∞}$]（下界と上界を負の無限大と正の無限大）とする
ミニマックス値の範囲を狭める ことができる null window search を行う
1 回の null window search で ミニマックス値の範囲が狭まる ので、null window search を 複数回繰り返す ことでいつかは 下界と上界が等しくなり、正確なミニマックス値を計算 することができる

MTD(f) の 具体的なアルゴリズム は以下の通りです。このアルゴリズムでミニマックス値を求めることができる理由について少し考えてみて下さい。

何らかの方法で $\boldsymbol{N}$ の ミニマックス値の近似値を推定 し、その値を $\boldsymbol{f}$ とする。ただし、$\boldsymbol{f}$ は整数 とする
$\boldsymbol{N}$ の ミニマックス値の範囲 を [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] とする
ミニマックス値の 下界と上界が等しくなる（ミニマックス値の範囲が 1 つの値になる）まで下記の 処理を繰り返す
1. $\boldsymbol{β}$ を 下記のように設定 する
  - $\boldsymbol{f}$ が 下界と等しい場合 は $\boldsymbol{β = f + 1}$ とする
  - $\boldsymbol{f}$ が 下界と等しくない場合 は $\boldsymbol{β = f}$ とする
2. $\boldsymbol{α = β - 1}$ とした ($\boldsymbol{β - 1}$, $\boldsymbol{β}$) という、ウィンドウ幅が 1 の null window search で $N$ の αβ 値を計算 し、その値を $\boldsymbol{g}$ とする
3. 上記で計算した $\boldsymbol{g}$ の値に応じて 下界または上界 を下記のように 更新する
  - $\boldsymbol{β ≦ g}$ の場合は fail high なので 下界を $\boldsymbol{g}$ で更新 する
  - それ以外（$\boldsymbol{g < β}$）の場合は fail low なので 上界を $\boldsymbol{g}$ で更新 する
4. $\boldsymbol{f}$ を $\boldsymbol{g}$ で更新 する
$\boldsymbol{f}$ が $N$ の ミニマックス値として計算 される

上記の 手順 1 で $\boldsymbol{f}$ を整数とした理由 は以下の通りです。

$N$ のミニマックス値として負の無限大や正の無限大を推定するのは明らかに変
$f$ が整数でない場合は、手順 3-2 の ($β - 1$, $β$) というウィンドウの中に評価値として計算される可能性がある整数の値が含まれてしまうため、以前の記事で説明したように null window search ではなくなる
下記のノートで説明するが、($β - 1$, $β$) というウィンドウの中に評価値として計算される可能性がある値が含まれてしまうと、手順 3-3 で $\boldsymbol{g < β}$ の場合 に exact value となる可能性が生じてしまう

上記の手順 3-3 で、$\boldsymbol{g < β}$ の場合は fail low となる理由は以下の通りです。

評価値として整数のみが計算されるので $g$ は整数である
手順 1 の $f$ は整数で、手順 3-4 で $f$ は $g$ で更新されるので $f$ は常に整数である
従って、手順 3-1 で計算される $β$ も常に整数である
($β - 1$, $β$) というウィンドウの範囲に評価値として計算される整数の値は存在しないので、$g$ が exact value の範囲になることはない
従って $g$ が fail high でない $\boldsymbol{g < β}$ の場合は fail low となる

$N$ のミニマックス値を推定する手法としては、まだ本記事で紹介していない反復深化を利用するのが一般的だと思います。

MTD(f) 法で行なわれる計算の分類

上記のアルゴリズムの 手順 3-2 の null window search の ウィンドウ は、$\boldsymbol{f}$ とミニマックス値の上界、下界の値 によって決まります。そこで、前回の記事と同様に、手順 3 で行なわれる処理 を、$f$ の分類、ミニマックス値の上界、下界の 3 種類の情報の組み合わせで分類 して説明します。その際に 3 種類の情報を下記のように記述 します。

$f$ の分類, [下界, 上界]

最初の null window search の分類

MTD(f) 法では最初は ミニマックス値の範囲 を [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] として処理を始めます。また、$\boldsymbol{N}$ の ミニマックス値が $\boldsymbol{s}$ の場合に、手順 1 で $N$ の ミニマックス値として推定した $\boldsymbol{f}$ は 以下の 3 通りの場合 があります。

$f < s$
$f = s$
$f > s$

従って、最初の null window search で行われる処理は下記の 3 種類に分類 されます。

$f < s$, [$-∞$, $∞$]
$f = s$, [$-∞$, $∞$]
$f > s$, [$-∞$, $∞$]

それぞれの場合で行われる処理について検証します。

f < s, [-∞, ∞] の場合に行なわれる処理

この分類の場合は、手順 3 で下記のような処理が行われます。

$\boldsymbol{f}$ は 下界の値 である負の無限大と 等しくない ので、手順 3-1 で $\boldsymbol{β = f}$ となる
手順 3-2 で ($β - 1$, $β$)、すなわち ($\boldsymbol{f - 1}$, $\boldsymbol{f}$) をウィンドウ とした null window search で $N$ の αβ 値である $\boldsymbol{g}$ を計算する

$\boldsymbol{β = f < s}$ なので $\boldsymbol{g}$ は fail high の範囲 となります。従って $\boldsymbol{β = f ≦ g}$ となります。

また、$g$ が fail high の範囲の場合 は、ミニマックス値 $\boldsymbol{s}$ は $\boldsymbol{g}$ 以上であるという意味になるので、$\boldsymbol{g ≦ s}$ となります。

上記から、$\boldsymbol{g}$ は $\boldsymbol{f ≦ g ≦ s}$ を満たす整数 となります。

次の 手順 3-3 では $g$ は fail high の範囲（$\boldsymbol{β ≦ g}$）なので、下界が $\boldsymbol{g}$ で更新 されます。

上記をまとめると以下のようになります。

$\boldsymbol{f < s}$, [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] の場合は null window search の結果、以下の処理 が行われる。

$\boldsymbol{f}$ が $\boldsymbol{f ≦ g ≦ s}$ を 満たす整数 $\boldsymbol{g}$ で更新 される
従って、更新後の $\boldsymbol{f}$ は 更新前の $\boldsymbol{f}$ 以上の値 になる
ミニマックス値の範囲 が [$―∞$, $∞$] から [$\boldsymbol{f}$, $\boldsymbol{∞}$] になり、必ず狭くなる

記号だけの説明ではわかりづらいと思いますので、具体例を挙げて説明します。

$f = 0$、$s = 5$ の場合は、手順 3-1 で $β = 0$ となり、手順 3-2 で行なわれる null window search のウィンドウは下図のように (-1, 0) となります。

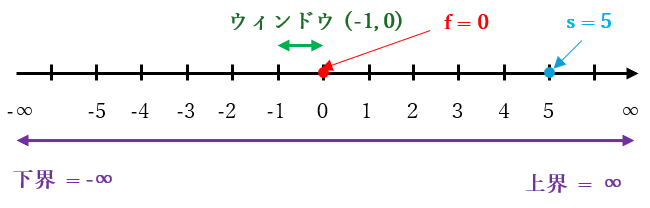
上記の null window search の計算結果である $g$ は $f ≦ g ≦ s$ を満たす整数、すなわち 0 以上 5 以下の整数 が計算されます。例えば 2 が計算された場合は $\boldsymbol{f}$ と下界は 2 で更新される ので、下図のようになります。

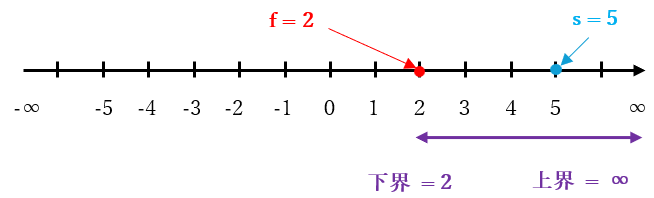
手順 3-3 を計算した結果、ミニマックス値の範囲 は [$\boldsymbol{f}$, $\boldsymbol{∞}$] となりますが、上界と下界は等しくない ので、次の null window search が行なわれます。その際に、更新された $\boldsymbol{f}$ の値によって下記の 2 通りに分類する ことができるので、それぞれの場合について検証します。

$f < s$, [$f$, $∞$]
$f = s$, [$f$, $∞$]

f < s, [f, ∞] の場合

この分類の場合は、手順 3 で下記のような処理が行われます。

$\boldsymbol{f =}$ 下界なので、手順 3-1 で $\boldsymbol{β = f + 1}$ となる
手順 3-2 で ($β - 1$, $β$)、すなわち ($\boldsymbol{f}$, $\boldsymbol{f + 1}$) をウィンドウ とした null window search で $N$ の αβ 値である $\boldsymbol{g}$ を計算する

下記の理由から $\boldsymbol{g}$ が fail low や exact value となることはない ので、$\boldsymbol{g}$ は必ず fail high の範囲 となります。従って $\boldsymbol{β = f + 1 ≦ g}$ となります。

以下の理由から $\boldsymbol{g}$ が fail low の範囲になることはない
- $\boldsymbol{g}$ が fail low の場合は $g ≦ α$、すなわち $\boldsymbol{g ≦ f}$ である
- $\boldsymbol{g}$ が fail low の場合は ミニマックス値 $\boldsymbol{s}$ が $\boldsymbol{g}$ 以下 であることを意味するので $\boldsymbol{s ≦ g}$ である
- 上記から $\boldsymbol{g}$ が fail low の場合は $\boldsymbol{s ≦ g ≦ f}$ となるが、これは $\boldsymbol{f < s}$ という前提に反する
以下の理由から $\boldsymbol{g}$ が exact value の範囲になることはない
- $\boldsymbol{f}$ は整数 なので、($f$, $f + 1$) という ウィンドウの範囲内 に 評価値がとりうる整数の値は存在しない
- 従って exact value となる $f < g < f + 1$ を満たす $g$ が計算されることはない

また、先程検証した $f < s$, [$-∞$, $∞$] の場合と同じ理由で $\boldsymbol{g ≦ s}$ となるので、$\boldsymbol{g}$ は $\boldsymbol{f + 1 ≦ g ≦ s}$ を満たす整数 となります。

次の 手順 3-3 では $g$ は fail high の範囲（$\boldsymbol{β ≦ g}$）なので、下界が $\boldsymbol{g}$ で更新 されます。その結果、ミニマックス値の範囲 は [$f$, $∞$] から [$\boldsymbol{g}$, $\boldsymbol{∞}$] に更新 されますが、$f < f + 1 ≦ g$ なので、$\boldsymbol{f < g}$ となるため、更新後の ミニマックス値の範囲は必ず狭くなります。

上記をまとめると以下のようになります。

$\boldsymbol{f < s}$, [$\boldsymbol{f}$, $\boldsymbol{∞}$] の場合は null window search の結果、以下の処理 が行われる。

$\boldsymbol{f}$ が $\boldsymbol{f < g ≦ s}$ を 満たす整数 $\boldsymbol{g}$ で更新 される
従って、更新後の $\boldsymbol{f}$ は 更新前の $\boldsymbol{f}$ よりも大きく なる
ミニマックス値の範囲 が [$f$, $∞$] から [$\boldsymbol{g}$, $\boldsymbol{∞}$] になり、必ず狭くなる

具体例を挙げます。$f = 2 < s = 5$, [$2$, $∞$] の場合は、手順 3-1 で $β = 3$ となり、手順 3-2 で行なわれる null window search のウィンドウは下図のように (2, 3) となります。

なお、下記の図から 手順 3-1 で $\boldsymbol{f =}$ 下界の場合に $\boldsymbol{β = f + 1}$ とした理由 が、ウィンドウ をミニマックス値の範囲内の 左端に合わせるため であることがわかります。

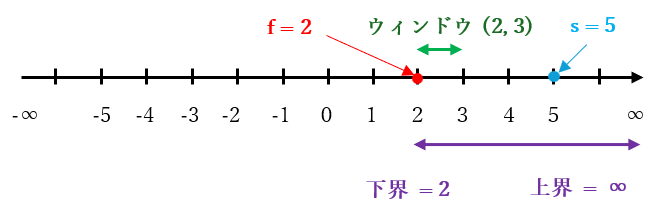
上記の null window search の計算結果は $f + 1 ≦ g ≦ s$ を満たす整数、すなわち 3 以上 5 以下の整数が計算 されます。例えば 3 が計算された場合は $\boldsymbol{f}$ と下界は 3 で更新される ので、下図のようになります。

上記を計算した結果、ミニマックス値の範囲 は [$\boldsymbol{f}$, $\boldsymbol{∞}$] となりますが、上界と下界は等しくない ので、次の null window search が行なわれます。その際に、更新された $\boldsymbol{f}$ の値によって下記の 2 通りに分類する ことができます。

$f < s$, [$f$, $∞$]
$f = s$, [$f$, $∞$]

前者は今回行った null window search と 同じ分類 になります。そのため、$\boldsymbol{f < s}$, [$\boldsymbol{f}$, $\boldsymbol{∞}$] という分類の null window search が無限に繰り返される可能性があると思う人がいるかもしれませんが、上記で示したように 更新後の $\boldsymbol{f}$ は必ず 更新前の値よりも大きく なります。また、更新後の $f$ の 最大値は $\boldsymbol{s}$ なので無限に繰り返されることはなく、いつかは $\boldsymbol{f = s}$, [$\boldsymbol{f}$, $\boldsymbol{∞}$] という 後者の分類の null window search が行なわれます。

上記で検証したように、$f < s$, [$f$, $∞$] の分類の null window search では、ミニマックス値の範囲が必ず狭くなる ため、無限に繰り返すことはできない と説明することもできます。

後者は先程検証した $\boldsymbol{f < s}$, [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] の次で行なわれる null window search の 2 つ目の分類と同じ です。そこで、次はこの後者の分類を検証することにします。

f = s, [f, ∞] の場合

この分類の場合は、手順 3 で下記のような処理が行われます。

$\boldsymbol{f =}$ 下界で $\boldsymbol{f = s}$ なので、手順 3-1 で $\boldsymbol{β = f + 1 = s + 1}$ となる
手順 3-2 で ($β - 1$, $β$)、すなわち ($\boldsymbol{s}$, $\boldsymbol{s + 1}$) をウィンドウ とした null window search で $N$ の αβ 値である $\boldsymbol{g}$ を計算する

$\boldsymbol{α = s}$ なので $\boldsymbol{g}$ は必ず fail low の範囲 となります。従って $\boldsymbol{g ≦ α = s}$ となります。

また、$g$ が fail low の範囲の場合 は、ミニマックス値 $\boldsymbol{s}$ は $\boldsymbol{g}$ 以下であるという意味になるので、$\boldsymbol{s ≦ g}$ となります。

$\boldsymbol{g ≦ s}$ と $\boldsymbol{s ≦ g}$ を同時に満たす $g$ は $s$ しかないので、$\boldsymbol{g = s}$ となります。

次の 手順 3-3 では $g$ は fail low の範囲（$\boldsymbol{g < β}$）なので、上界が $\boldsymbol{g}$ で更新 されます。その結果、ミニマックス値の範囲 は [$s$, $∞$] から [$\boldsymbol{s}$, $\boldsymbol{s}$] に更新 されて 上界と下界が等しくなりまる。従って、手順 3 の 繰り返し処理が終了 し、手順 4 で $\boldsymbol{f}$ に $N$ の ミニマックス値が計算 されます。

具体例を挙げます。$f = s = 5$, [$5$, $∞$] の場合は、手順 3-1 で $β = 6$ となり、手順 3-2 で行なわれる null window search のウィンドウは下図のように (5, 6) となります。

上記の null window search の計算結果は下図のように $f = s = 5$ のまま変化しませんが、下界と上界が等しくなり、$\boldsymbol{f}$ に正しいミニマックス値 である 5 が計算 されます。

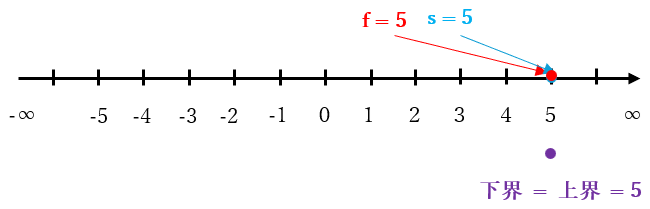
手順 1 で f < s の場合に行われる処理のまとめ

上記から、手順 1 で $\boldsymbol{f < s}$ の場合に行なわれる処理は、以下の表のようになります。

下記の表では $\boldsymbol{n}$ 回の null window search が行なわれた場合の例で、手順 1 で計算された $\boldsymbol{f}$ を $\boldsymbol{f_0}$、$\boldsymbol{i}$ 回目の null window search によって更新された $\boldsymbol{f}$ を $\boldsymbol{f_i}$ と表記します。また、「MM の範囲」の列は αβ 値の計算後に更新された ミニマックス値の範囲 を表します。

回数	分類	ウィンドウ	αβ 値	αβ の範囲	MM の範囲
1	$f < s$, [$-∞$, $∞$]	($f_0 - 1$, $f_0$)	$f_1$	fail high	[$f_1$, $∞$]
2	$f < s$, [$f$, $∞$]	($f_1$, $f_1 + 1$)	$f_2$	fail high	[$f_2$, $∞$]
3	$f < s$, [$f$, $∞$]	($f_2$, $f_2 + 1$)	$f_3$	fail high	[$f_3$, $∞$]
4	$f < s$, [$f$, $∞$]	($f_3$, $f_3 + 1$)	$f_4$	fail high	[$f_4$, $∞$]
・・・	・・・	・・・	・・・	・・・	・・・
$n-1$	$f < s$, [$f$, $∞$]	($f_{n-2}$, $f_{n-2} + 1$)	$f_{n-1}=s$	fail high	[$f_{n-1}$, $∞$] = [$s$, $∞$]
$n$	$f = s$, [$f$, $∞$]	($f_{n-1}$, $f_{n-1} + 1$)	$f_n=s$	fail low	[$f_{n-1}$, $f_n$] = [$s$, $s$]

ただし、$\boldsymbol{f = f_0 ≦ f_1 < f_2 < f_3 < ・・・ < f_{n-1} = f_{n} = s}$ となります。

上記の表をまとめると以下のようになります。

手順 1 で計算される $f$ が $\boldsymbol{f < s}$ の場合に、$\boldsymbol{n}$ 回の null window search が行なわれた場合は、以下の処理が行われる。

null window search が行われるたび に下記のように ミニマックス値の範囲が狭まっていく ことでミニマックス値を求めることができる
$\boldsymbol{n - 1}$ 回目まで の null window search では、$\boldsymbol{f}$ と ミニマックス値の下界 が $\boldsymbol{s}$ に向かって増えていく ことでミニマックス値の範囲が狭まる
ただし、初回のみ $f$ が 変化しない場合 があるが、その場合でも下界が $-∞$ から $f$ に更新されるので ミニマックス値の範囲は狭まる
$\boldsymbol{n - 1}$ 回目の null window search によって $\boldsymbol{f}$ がミニマックス値である $\boldsymbol{s}$ に更新される が、その時点ではミニマックス値の 上界が $\boldsymbol{∞}$ なので もう一回 null window search を行う必要がある
最後の null window search では下界は変化せず、上界が $\boldsymbol{s}$ に更新 されることで ミニマックス値が計算される

手順 1 で f < s の場合の処理の効率

手順 1 で $\boldsymbol{f < s}$ の場合に行なわれる 処理の効率 は、何回目の null window search で αβ 値に $\boldsymbol{s}$ が計算されるか によって異なります。

最も効率が良い のが 初回の null window search で $\boldsymbol{s}$ が計算された場合 で、2 回目 の null window search で ミニマックス値が計算される ので、最低 2 回の null window search が必要 となります。

例えば $f_0 = 0$, $s = 5$ の場合に、初回の null window search で 5 が計算された場合は以下のようになります。

回数	分類	ウィンドウ	αβ 値	αβ の範囲	MM の範囲
1	$f < s$, [$-∞$, $∞$]	($-1$, $0$)	$f_1 = s = 5$	fail high	[$5$, $∞$]
2	$f=s$, [$f$, $∞$]	($5$, $6$)	$f_2 = s = 5$	fail low	[$5$, $5$]

また、2 回目から $\boldsymbol{n - 1}$ 回目まで の null window search では必ず $\boldsymbol{f}$ が最低でも 1 ずつ増える ため、初回と $n$ 回目で $f$ が増えない場合を加えると、最大で $\boldsymbol{s - f + 2}$ 回の null window search 行なわれます。

例えば $f_0 = 0$, $s = 5$ の場合で最悪の場合は以下のように、$5 - 0 + 2 = 7$ 回の null window search が必要になります。

回数	分類	ウィンドウ	αβ 値	αβ の範囲	MM の範囲
1	$f < s$, [$-∞$, $∞$]	($-1$, $0$)	$f_1 = 0$	fail high	[$0$, $∞$]
2	$f < s$, [$0$, $∞$]	($-1$, $0$)	$f_2 = 1$	fail high	[$1$, $∞$]
3	$f < s$, [$0$, $∞$]	($-1$, $0$)	$f_3 = 2$	fail high	[$2$, $∞$]
4	$f < s$, [$0$, $∞$]	($-1$, $0$)	$f_4 = 3$	fail high	[$3$, $∞$]
5	$f < s$, [$0$, $∞$]	($-1$, $0$)	$f_5 = 4$	fail high	[$4$, $∞$]
6	$f < s$, [$0$, $∞$]	($-1$, $0$)	$f_6 = s = 5$	fail high	[$5$, $∞$]
7	$f = s$, [$0$, $∞$]	($-1$, $0$)	$f_7 = s = 5$	fail low	[$5$, $5$]

上記から 以下の順で null window search が行われる ことがわかります。

$f < s$, [$-∞$, $∞$] の分類が 1 回
$f < s$, [$f$, $∞$] の分類が 0 ～ $\boldsymbol{s - f}$ 回。$f_i$ が $s$ に向けて毎回増えていく
$f = s$, [$f$, $∞$] の分類が 1 回

上記から下記の事がわかります。

手順 1 で計算される $f$ が $f < s$ の場合に行なわれる処理は以下のようになる。

最善で 2 回 の null window search が必要となる
最悪で $\boldsymbol{s - f + 2}$ 回の null window search が必要となる
従って、$N$ のミニマックス値の推定値 $\boldsymbol{f}$ の精度が高い程 MTD(f) の 処理の効率が高くなる ことが期待できる

具体例として $\boldsymbol{f_0 = 0, f_1=2, f_2=3, f_3=5, f_4=5、s = 5}$ の場合の処理を下図に並べます。$f$ と下界が 5 に向かって増えていき、最後に上界が 5 となる様子をして下さい。

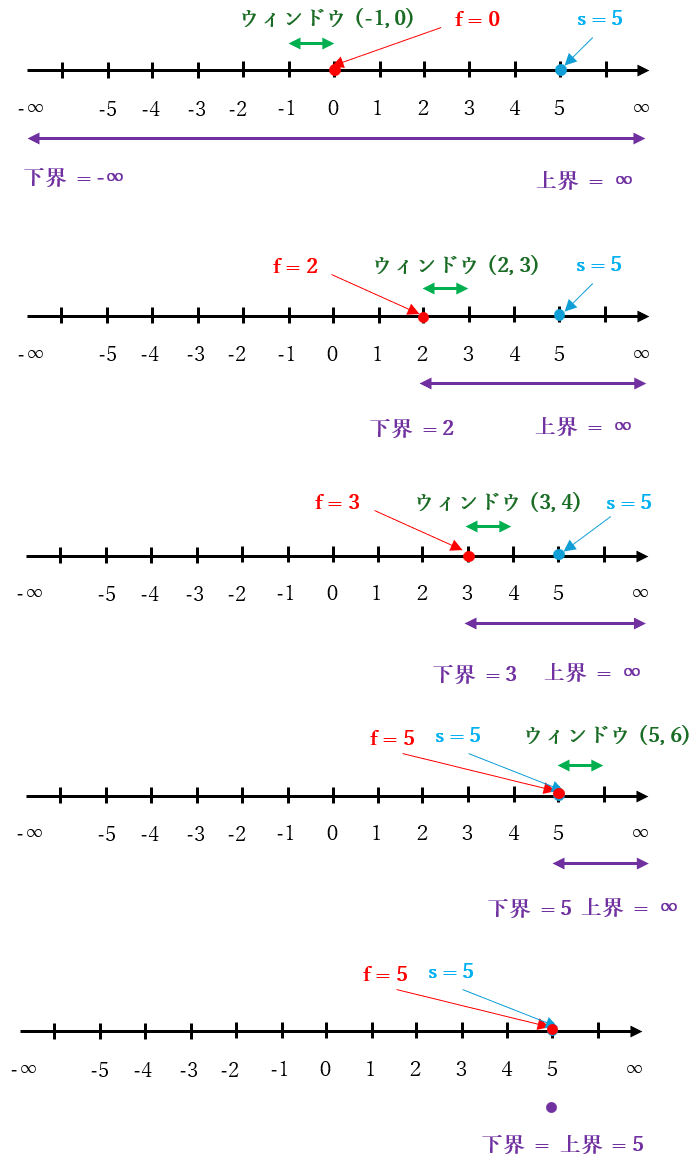
f = s, [-∞, ∞] の場合に行なわれる処理

最初の null window search の分類 が $\boldsymbol{f = s}$, [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] の場合の処理を検証します。

この場合は、下記のような処理が行われます。

$\boldsymbol{f}$ は 下界の値 である負の無限大と 等しくない ので、手順 3-1 で $\boldsymbol{β = f = s}$ となる
手順 3-2 で ($β - 1$, $β$)、すなわち ($\boldsymbol{s - 1}$, $\boldsymbol{s}$) をウィンドウ とした null window search で $N$ の αβ 値である $\boldsymbol{g}$ を計算する

$\boldsymbol{β = s}$ なので $\boldsymbol{g}$ は必ず fail high の範囲 となります。従って $\boldsymbol{β = s ≦ g}$ となります。

$\boldsymbol{s ≦ g}$ と $\boldsymbol{g ≦ s}$ を同時に満たす $g$ は $s$ しかないので、$\boldsymbol{g = s}$ となります。

次の 手順 3-3 では $g$ は fail high 範囲（$\boldsymbol{β ≦ g}$）なので、下界が $\boldsymbol{g = s}$ で更新 されます。その結果、ミニマックス値の範囲 は [$-∞$, $∞$] から [$\boldsymbol{s}$, $\boldsymbol{∞}$] に更新 されます。

上記をまとめると以下のようになります。

$\boldsymbol{f = s}$, [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] の場合は null window search の結果、以下の処理 が行われる。

$\boldsymbol{f}$ が $\boldsymbol{s}$ で更新 される
ミニマックス値の範囲 が [$-∞$, $∞$] から [$\boldsymbol{s}$, $\boldsymbol{∞}$] になり、必ず狭くなる

次の null window search の分類は $\boldsymbol{f=s}$, [$\boldsymbol{f}$, $\boldsymbol{∞}$] となりますが、この分類は先程検証済み です。従って、$\boldsymbol{f = s}$, [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] の場合は下記の表のように、必ず 2 回の null window search が行なわれます。

回数	分類	ウィンドウ	αβ 値	αβ の範囲	MM の範囲
1	$f = s$, [$-∞$, $∞$]	($s - 1$, $s$)	$f_1 = s$	fail high	[$f_1$, $∞$] = [$s$, $∞$]
2	$f = s$, [$f$, $∞$]	($s$, $s + 1$)	$f_2=s$	fail low	[$f_1$, $f_2$] = [$s$, $s$]

上記をまとめると以下のようになります。

手順 1 で計算される $f$ が $\boldsymbol{f = s}$ の場合に行なわれる処理は以下のようになる。

1 回目の null window search でミニマックス値の範囲が [$s$, $∞$] になる
2 回目の null window search でミニマックス値の範囲が [$s$, $s$] になる
従って 必ず 2 回 の null window search が行われる

f > s, [-∞, ∞] の場合に行なわれる処理

最初の null window search の分類 が $\boldsymbol{f > s}$, [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] の場合の 処理の検証 は、$\boldsymbol{f < s}$, [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] の場合の 処理の検証とほぼ同じ ですが、少しだけ異なる 点があります。

この分類の場合は、手順 3 で下記のような処理が行われます。

$\boldsymbol{f}$ は 下界の値 である負の無限大と 等しくない ので、手順 3-1 で $\boldsymbol{β = f}$ となる
手順 3-2 で ($β - 1$, $β$)、すなわち ($\boldsymbol{f - 1}$, $\boldsymbol{f}$) をウィンドウ とした null window search で $N$ の αβ 値である $\boldsymbol{g}$ を計算する

$\boldsymbol{f}$ と $\boldsymbol{s}$ は整数で $f > s$ なので、$\boldsymbol{f - 1 ≧ s}$ となります。$α = f - 1$ なので $\boldsymbol{s ≦ α}$ となるので、$\boldsymbol{g}$ は必ず fail low の範囲 となります。従って $\boldsymbol{g ≦ α = f - 1}$ となります。

上記から、$\boldsymbol{g}$ は $\boldsymbol{s ≦ g ≦ f - 1}$ を満たす整数 となります。

$\boldsymbol{f < s}$, [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] の場合では、$\boldsymbol{f ≦ g ≦ s}$ だったので、こちらの場合は $\boldsymbol{s ≦ g ≦ f}$ となると思った人がいるかもしれませんが、実際には $\boldsymbol{s ≦ g ≦ f - 1}$ となる点に注意して下さい。

次の 手順 3-3 では $g$ は fail low の範囲（$\boldsymbol{g < β}$）なので、上界が $\boldsymbol{g}$ で更新 されます。

上記をまとめると以下のようになります。

$\boldsymbol{f > s}$, [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] の場合は null window search の結果、以下の処理 が行われる。

$\boldsymbol{f}$ が $\boldsymbol{s ≦ g ≦ f - 1}$ を 満たす整数 $\boldsymbol{g}$ で更新 される
従って、更新後の $\boldsymbol{f}$ は 更新前の $\boldsymbol{f}$ より小さな値 になる
ミニマックス値の範囲 が [$―∞$, $∞$] から [$\boldsymbol{-∞}$, $\boldsymbol{f}$] になり、必ず狭くなる

$f < s$, [$-∞$, $∞$] の場合は更新後の $f$ は更新前の $f$ 以上の値 になりますが、$f > s$, [$-∞$, $∞$] の場合は 更新前の $\boldsymbol{f}$ は更新前の $f$ 以下ではなく、$\boldsymbol{f}$ より小さな値になる点が異なります。

次の null window search は、更新された $f$ の値によって下記の 2 通りに分類することができます。

$f > s$, [$-∞$, $f$]
$f = s$, [$-∞$, $f$]

手順 1 で f > s の場合に行われる処理のまとめ

上記のそれぞれの場合で行なわれる処理は、先程検証した「$f < s$, [$f$, $∞$]」、「$f = s$, [$f$, $∞$]」と同様なので、その検証は省略し、結果だけをまとめることにします。余裕がある方は実際に検証してみて下さい。

手順 1 で $\boldsymbol{f < s}$ の場合に行なわれる処理は以下の表のようになります。

回数	分類	ウィンドウ	αβ 値	αβ 範囲	MM の範囲
1	$f > s$, [$-∞$, $∞$]	($f_0 - 1$, $f_0$)	$f_1$	fail low	[$-∞$, $f_1$]
2	$f > s$, [$-∞$, $f$]	($f_1 - 1$, $f_1$)	$f_2$	fail low	[$-∞$, $f_2$]
3	$f > s$, [$-∞$, $f$]	($f_2 - 1$, $f_2$)	$f_3$	fail low	[$-∞$, $f_3$]
4	$f > s$, [$-∞$, $f$]	($f_3 - 1$, $f_3$)	$f_4$	fail low	[$-∞$, $f_4$]
・・・	・・・	・・・	・・・	・・・	・・・
$n-1$	$f > s$, [$-∞$, $f$]	($f_{n-2} - 1$, $f_{n-2}$)	$f_{n-1}=s$	fail low	[$-∞$, $f_{n-1}$] = [$-∞$, $s$]
$n$	$f = s$, [$-∞$, $f$]	($f_{n-1} - 1$, $f_1$)	$f_n=s$	fail high	[$f_{n}$, $f_{n-1}$] = [$s$, $s$]

ただし、$\boldsymbol{f = f_0 > f_1 > f_2 > f_3 > ・・・ > f_{n-1} = f_{n} = s}$ となります。

$\boldsymbol{f < s}$, [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] の場合は $f = f_0 ≦ f_1$ でしたが、こちらでは $f = f_0 > f_1$ のように $≧$ ではなく $>$ となっている点が異なります。

上記の表をまとめると以下のようになります。

手順 1 で計算される $f$ が $\boldsymbol{f > s}$ の場合に、$\boldsymbol{n}$ 回の null window search が行なわれた場合は、以下の処理が行われる。

null window search が行われるたび に下記のように ミニマックス値の範囲が狭まっていく ことでミニマックス値を求めることができる
$\boldsymbol{n - 1}$ 回目まで の null window search では、$\boldsymbol{f}$ と ミニマックス値の上界 が $\boldsymbol{s}$ に向かって減っていく ことでミニマックス値の範囲が狭まる
$\boldsymbol{n - 1}$ 回目の null window search によって $\boldsymbol{f}$ がミニマックス値である $\boldsymbol{s}$ に更新される が、その時点ではミニマックス値の 下界が $\boldsymbol{∞}$ なので もう一回 null window search を行う必要がある
最後の null window search のみ 上界は変化せず、下界が $\boldsymbol{s}$ に更新 されることで ミニマックス値が計算される

また、以下の順で null window search が行われます。

$f > s$, [$-∞$, $∞$] の分類が 1 回
$f > s$, [$―∞$, $f$] の分類が 0 ～ $\boldsymbol{f - s - 1}$ 回。$f_i$ が $s$ に向けて毎回減って行く
$f = s$, [$-∞$, $f$] の分類が 1 回

$\boldsymbol{f < s}$, [$\boldsymbol{-∞}$, $\boldsymbol{∞}$] の場合と異なり、最初の null window search の αβ 値は $f$ 未満になるので、$f > s$, [$―∞$, $f$] の分類の回数は 0 ~ $f - s$ 回ではなく、0 ～ $\boldsymbol{f - s - 1}$ 回となります。

上記から下記の事がわかります。

手順 1 で計算される $f$ が $\boldsymbol{f > s}$ の場合に行なわれる処理は以下のようになる。

最善で 2 回 の null window search が必要となる
最悪で $\boldsymbol{f - s + 1}$ 回の null window search が必要となる
従って、$N$ のミニマックス値の推定値 $\boldsymbol{f}$ の精度が高い程 MTD(f) の 処理の効率が高くなる ことが期待できる

細かい話になりますが、手順 1 で計算される $f$ が $f > s$ の場合は、$f = s + 1$ が計算された場合でも常に最も効率が良い 2 回の null window search が行なわれます。

MTD(f) 法の効率

null window search は ($-∞$, $∞$) のウィンドウで計算する αβ 法よりも 枝狩りの効率が大幅に高い ので、少ない回数の null window search であれば、複数回行っても ($-∞$, $∞$) のウィンドウの αβ 法よりも短い時間で計算 を行うことができる 可能性が高くなります。

MTD(f) 法では 手順 1 で計算される $\boldsymbol{f}$ の値によって 以下の表の回数 の null window search が行なわれます。

条件	最小回数	最大回数
$\boldsymbol{f < s}$	$2$	$s - f + 2$
$\boldsymbol{f = s}$	$2$	$2$
$\boldsymbol{f > s}$	$2$	$f - s + 1$

上記の表から 正確なミニマックス値を計算できた場合 は、MTD(f) 法で 最も効率が高い 2 回の null window search でミニマックス値を計算することができ、そうでない場合は $|\boldsymbol{f - s}|$²が大きいほど null window search の 回数が増える可能性が高くなる ことがわかります。従って、MTD(f) 法では手順 1 で計算される $\boldsymbol{f}$ の精度が高いことが非常に重要 となります。

また、MTD(f) 法では、同じ $\boldsymbol{N}$ に対して 異なるウィンドウで複数回の αβ 値を計算 するので、同じ子孫ノードに対して何度も αβ 値を計算 することになります。そのため、置換表を利用 することで 効率を大幅に向上させることが期待できます。

上記に関する MTD(f) 法の効率の検証については、次回の記事で行います。

`ai_mtdf` の実装

MTD(f) のアルゴリズムで着手を選択する ai_mtdf という 関数を定義 する事にします。MTD(f) で行う null window search は ai_abs_all 内で定義 されているローカル関数 ab_search をそのまま利用できる ので、ai_abs_all を下記のプログラムのように修正して ai_mtdf を定義することにします。

なお、MTD(f) 法は置換表を利用することが前提のアルゴリズムですが、置換表を利用しない場合と比較できるように、置換表の利用の有無を ai_abs_all と同様に選択できるようにします。また、MTD(f) 法の論文では move ordering を行っていませんが move ordering を行なった場合と比較できるように move ordering の有無も選択できるようにします。

6 行目：関数名を ai_mtdf に修正する
7 行目：手順 1 の $N$ の推定値である $f$ を代入するための仮引数 f を、デフォルト値を 0 とするデフォルト引数として追加する
10、11 行目：ミニマックス値の下界と上界を表すローカル変数 lbound と ubound を初期化する。先程のアルゴリズムの説明ではそれぞれの初期値を負の無限大と正の無限大としたが、init_ab が True の場合は評価値の最小値と最大値を設定する。なお、lower_bound と upper_bound という変数はローカル関数 ab_search 内で別の用途で利用しているのでそれらとは異なる名前とした
13 行目：これから行う複数回の null window search で利用する置換表を表す tt を空の dict で初期化する
14 行目：下界と上界が等しくなるまで 15 ~ 20 行目の処理を繰り返す
15 行目：手順 3-1 の $β$ を計算する
16 行目：手順 3-2 の null window search を行う。手順 3-2 では更新前の $f$ と更新後の $f$ を区別できるように計算した αβ 値を $g$ と表記したが、手順 3-4 で $f$ を $g$ で更新するので、16 行目では f の値を計算した αβ 値で更新した
17 ~ 20 行目：手順 3-3 の下界または上界を更新する処理を行う
21 行目：繰り返しの終了後に f にミニマックス値が計算されるので、score に f を代入する

 1  from ai import ai_by_score, dprint
 2  from marubatsu import Marubatsu
 3  from copy import deepcopy
 4  
 5  @ai_by_score
 6  def ai_mtdf(mb, debug=False, shortest_victory=False, init_ab=False, use_tt=False, 
 7                 f=0, ai_for_mo=None, params={}, sort_allnodes=False, calc_count=False):  
元と同じなので省略         
 8      min_score = -2 if shortest_victory else -1
 9      max_score = 3 if shortest_victory else 1
10      lbound = min_score if init_ab else float("-inf")
11      ubound = max_score if init_ab else float("inf")
12  
13      tt = {}
14      while lbound != ubound:
15          beta = f + 1 if lbound == f else f
16          f = ab_search(mb, tt, alpha=beta - 1, beta=beta)
17          if f >= beta:
18              lbound = f
19          else:
20              ubound = f
21      score = f
22              
23      dprint(debug, "count =", count)
24      if calc_count:
25          return count
26      if mb.turn == Marubatsu.CIRCLE:
27          score *= -1
28      return score

行番号のないプログラム

from ai import ai_by_score, dprint
from marubatsu import Marubatsu
from copy import deepcopy

@ai_by_score
def ai_mtdf(mb, debug=False, shortest_victory=False, init_ab=False, use_tt=False, 
               f=0, ai_for_mo=None, params={}, sort_allnodes=False, calc_count=False):           
    count = 0
    def ab_search(mborig, tt, alpha=float("-inf"), beta=float("inf")):
        nonlocal count
        count += 1
        if mborig.status == Marubatsu.CIRCLE:
            return (11 - mborig.move_count) / 2 if shortest_victory else 1
        elif mborig.status == Marubatsu.CROSS:
            return (mborig.move_count - 10) / 2 if shortest_victory else -1
        elif mborig.status == Marubatsu.DRAW:
            return 0
        
        if use_tt:
            boardtxt = mborig.board_to_str()
            if boardtxt in tt:
                lower_bound, upper_bound = tt[boardtxt]
                if lower_bound == upper_bound:
                    return lower_bound
                elif upper_bound <= alpha:
                    return upper_bound
                elif beta <= lower_bound:
                    return lower_bound
                else:
                    alpha = max(alpha, lower_bound)
                    beta = min(beta, upper_bound)
            else:
                lower_bound = min_score
                upper_bound = max_score
        
        alphaorig = alpha
        betaorig = beta

        legal_moves = mborig.calc_legal_moves()
        if ai_for_mo is not None:
            if sort_allnodes:
                score_by_move = ai_for_mo(mborig, analyze=True, **params)["score_by_move"]
                score_by_move_list = sorted(score_by_move.items(), key=lambda x:x[1], reverse=True)
                legal_moves = [x[0] for x in score_by_move_list]
            else:
                legal_moves = mborig.calc_legal_moves()
                bestmove = ai_for_mo(mborig, rand=False, **params)
                index = legal_moves.index(bestmove)
                legal_moves[0], legal_moves[index] = legal_moves[index], legal_moves[0]
        if mborig.turn == Marubatsu.CIRCLE:
            score = float("-inf")
            for x, y in legal_moves:
                mb = deepcopy(mborig)
                mb.move(x, y)
                score = max(score, ab_search(mb, tt, alpha, beta))
                if score >= beta:
                    break
                alpha = max(alpha, score)
        else:
            score = float("inf")
            for x, y in legal_moves:
                mb = deepcopy(mborig)
                mb.move(x, y)
                score = min(score, ab_search(mb, tt, alpha, beta))
                if score <= alpha:
                    break
                beta = min(beta, score)   
            
        from util import calc_same_boardtexts

        if use_tt:
            boardtxtlist = calc_same_boardtexts(mborig)
            if score <= alphaorig:
                upper_bound = score
            elif score < betaorig:
                lower_bound = score
                upper_bound = score
            else:
                lower_bound = score
            for boardtxt in boardtxtlist:
                tt[boardtxt] = (lower_bound, upper_bound)
        return score
                
    min_score = -2 if shortest_victory else -1
    max_score = 3 if shortest_victory else 1
    lbound = min_score if init_ab else float("-inf")
    ubound = max_score if init_ab else float("inf")

    tt = {}
    while lbound != ubound:
        beta = f + 1 if lbound == f else f
        f = ab_search(mb, tt, alpha=beta - 1, beta=beta)
        if f >= beta:
            lbound = f
        else:
            ubound = f
    score = f
            
    dprint(debug, "count =", count)
    if calc_count:
        return count
    if mb.turn == Marubatsu.CIRCLE:
        score *= -1
    return score

修正箇所

from ai import ai_by_score, dprint
from marubatsu import Marubatsu
from copy import deepcopy

@ai_by_score
-def ai_abs_all(mb, debug=False, shortest_victory=False, init_ab=False, use_tt=False, 
-               ai_for_mo=None, params={}, sort_allnodes=False, calc_count=False):  
+def ai_mtdf(mb, debug=False, shortest_victory=False, init_ab=False, use_tt=False, 
+            f=0, ai_for_mo=None, params={}, sort_allnodes=False, calc_count=False):  
元と同じなので省略         
    min_score = -2 if shortest_victory else -1
    max_score = 3 if shortest_victory else 1
-   alpha = min_score if init_ab else float("-inf")
-   beta = max_score if init_ab else float("inf")
+   lbound = min_score if init_ab else float("-inf")
+   ubound = max_score if init_ab else float("inf")

-   score = ab_search(mb, {}, alpha=alpha, beta=beta)
+   tt = {}
+   while lbound != ubound:
+       beta = f + 1 if lbound == f else f
+       f = ab_search(mb, tt, alpha=beta - 1, beta=beta)
+       if f >= beta:
+           lbound = f
+       else:
+           ubound = f
+   f = score        
    
    dprint(debug, "count =", count)
    if calc_count:
        return count
    if mb.turn == Marubatsu.CIRCLE:
        score *= -1
    return score

上記の定義後に、以前の記事で ai_abs_all が 強解決であるかどうか を確認したのと同様の方法で ai_mtdf が強解決の AI であるか どうかを確認すると、実行結果から いずれの設定の場合でも強解決の AI であることが確認できます。

なお、MTD(f) はもともと move ordering を前提としないアルゴリズムなので、move ordering を行わない場合で検証 を行いました。

from util import Check_solved

for shortest_victory in [False, True]:
    for use_tt in [False, True]:
        for init_ab in [False, True]:
            for sort_allnodes in [False, True]:
                print(f"sv: {shortest_victory}, use_tt: {use_tt}, init_ab: {init_ab}")
                params = {
                    "shortest_victory": shortest_victory,
                    "init_ab": init_ab,
                    "use_tt": use_tt,
                }
                Check_solved.is_strongly_solved(ai_mtdf, params=params)

実行結果

sv: False, use_tt: False, init_ab: False
100%|██████████| 431/431 [00:04<00:00, 87.39it/s] 
431/431 100.00%
sv: False, use_tt: False, init_ab: True
100%|██████████| 431/431 [00:03<00:00, 124.23it/s]
431/431 100.00%
sv: False, use_tt: True, init_ab: False
100%|██████████| 431/431 [00:03<00:00, 127.08it/s]
431/431 100.00%
sv: False, use_tt: True, init_ab: True
100%|██████████| 431/431 [00:02<00:00, 149.80it/s]
431/431 100.00%
sv: True, use_tt: False, init_ab: False
100%|██████████| 431/431 [00:04<00:00, 88.04it/s] 
431/431 100.00%
sv: True, use_tt: False, init_ab: True
100%|██████████| 431/431 [00:05<00:00, 80.79it/s] 
431/431 100.00%
sv: True, use_tt: True, init_ab: False
100%|██████████| 431/431 [00:03<00:00, 123.87it/s]
431/431 100.00%
sv: True, use_tt: True, init_ab: True
100%|██████████| 431/431 [00:03<00:00, 113.19it/s]
431/431 100.00%

今回の記事のまとめ

今回の記事では MTD(f) 法について説明し、MTD(f) 法で着手を選択する ai_mtdf の定義を行いました。次回の記事では実装した ai_mtdf を利用して MTD(f) の効率を検証します。

本記事で入力したプログラム

リンク	説明
marubatsu.ipynb	本記事で入力して実行した JupyterLab のファイル
ai.py	本記事で更新した ai_new.py

次回の記事

MTD(f) を紹介した論文では move ordering を行なっていませんが、move ordering を行ってもかまいません ↩
$|x|$ は $x$ の絶対値（符号を正にした値）を表す記号です ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

Pythonで〇×ゲームのAIを一から作成する その168 MTD(f) 法の仕組みと実装

目次と前回の記事

これまでに作成したモジュール

MTD(f) 法

利用する記号

MTD(f) 法の特徴

MTD(f) 法の考え方とアルゴリズム

MTD(f) 法で行なわれる計算の分類

最初の null window search の分類

f < s, [-∞, ∞] の場合に行なわれる処理

f < s, [f, ∞] の場合

f = s, [f, ∞] の場合

手順 1 で f < s の場合に行われる処理のまとめ

手順 1 で f < s の場合の処理の効率

f = s, [-∞, ∞] の場合に行なわれる処理

f > s, [-∞, ∞] の場合に行なわれる処理

手順 1 で f > s の場合に行われる処理のまとめ

MTD(f) 法の効率

ai_mtdf の実装

今回の記事のまとめ

本記事で入力したプログラム

次回の記事

Pythonで〇×ゲームのAIを一から作成する　その168　MTD(f) 法の仕組みと実装

`ai_mtdf` の実装