Pythonで〇×ゲームのAIを一から作成する その167 完璧な move ordering での αβ 法とスカウト法

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

リンク	説明
marubatsu.py	Marubatsu、Marubatsu_GUI クラスの定義
ai.py	AI に関する関数
test.py	テストに関する関数
util.py	ユーティリティ関数の定義。現在は gui_play のみ定義されている
tree.py	ゲーム木に関する Node、Mbtree クラスの定義
gui.py	GUI に関する処理を行う基底クラスとなる GUI クラスの定義

AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。

完璧な move ordering での αβ 法とスカウト法の効率

前回の記事では move ordering の精度が 100 % の場合の αβ 法とスカウト法の効率が同じになる ことを示しました。今回の記事ではその理由を説明します。

なお、これまでは「move ordering の精度が 100 % の場合」のように表記していましたが、表記が長いので今後は短く「完璧な move ordering」と表記することにします。

説明で利用する記号等の説明

今回の記事では、αβ 法やスカウト法で計算を行う際の 各ノード を「max ノードか min ノードであるか」、「ミニマックス値」、「ウィンドウ」の 3 種類の情報の組み合わせ で 分類して説明 します。

その際に下記の記号を用い、3 種類の情報を ,（半角のカンマ） で区切って表記 します。

表記	意味
max	max ノード
min	min ノード
$\boldsymbol{s}$	ミニマックス値が $s$ である
$\boldsymbol{s_-}$	ミニマックス値が $s$ 以下である
$\boldsymbol{s_+}$	ミニマックス値が $s$ 以上である
$\boldsymbol{s_>}$	ミニマックス値が $s$ より大きい
(α 値の初期値, β 値の初期値)	ノードを計算する際のウィンドウの範囲

例えば「max ノード」、「ミニマックス値が $s$ 以下」、「ウィンドウが ($s$, $s + 1$)」のノードの分類は以下のように表記します。

max, $s_-$, ($s$, $s + 1$)

完璧な move ordering での αβ 法で行なわれる処理

まず、完璧な move ordering での αβ 法が行う処理 について説明します。

具体的には、下記の条件でノード $N$ の評価値を αβ 法で計算する場合の処理を説明します。

• $N$ は max ノードである
• $N$ のミニマックス値は $s$ である
• $N$ を計算する際の α 値と β 値の初期値を負の無限大と正の無限大とする
• $N$ と $N$ のすべての子孫ノードで、完璧な move ordering が行なわれている
• 置換表は利用しない

なお、本記事では説明を省略しますが「$N$ が min ノードの場合」、「$N$ を計算する際の α 値と β 値の初期値を、評価値の最小値と最大値に設定する場合」、「置換表を利用する場合」でも、同様の手順で行なわれる処理を説明することができるので、余裕がある方はそのような場合で行なわれる処理についても確認してみて下さい。

max, s, (-∞, ∞) のノードで行なわれる処理

$N$ の評価値を計算する際は「max ノード」、「ミニマックス値は $s$」、「ウィンドウは ($-∞$, $∞$)」なので、$N$ は「max, $s$, ($-∞$, $∞$)」に分類されます。

この分類のノードは max ノードで、そのミニマックス値は $s$ なので、子ノードの評価値の最大値は $\boldsymbol{s}$ となります。

完璧な move ordering では、max ノードの 先頭の子ノードのミニマックス値 は最大値である $\boldsymbol{s}$ となり、それ以外の子ノードのミニマックス値 は $\boldsymbol{s}$ 以下、すなわち $\boldsymbol{s_-}$ となります。

以下では 子ノードの分類 を行います。子ノードの数が 0 や 1 の場合は当然ですが、そのノードには下記の分類に対応する子ノードが存在しない場合があります。

最初の子ノードの計算処理

この分類のノードの 最初の子ノード は以下のように計算されるので「min, $\boldsymbol{s}$, ($\boldsymbol{-∞}$, $\boldsymbol{∞}$)」に 分類 されます。

• min ノードである
• このノードのウィンドウが受け継がれるのでウィンドウは ($-∞$, $∞$) となる
• ミニマックス値は $s$ である

また、最初の子ノードの評価値として $s$ が計算されるので、α 値 は -∞ から $\boldsymbol{s}$ に更新 され、次の子ノードの評価値を計算する際の ウィンドウが ($\boldsymbol{s}$, $\boldsymbol{∞}$) となります。

2 番目以降の子ノードの計算処理

この分類の 2 番目の子ノードは以下のように計算されるので「min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)」に 分類 されます。

• min ノードである
• ウィンドウは ($s$, $∞$) である
• ミニマックス値は $s_-$（$s$ 以下）である

$s_- ≦ s$ なので、α 値 は $s$ のまま 更新されません。従って、次の子ノードの評価値を計算する際の ウィンドウは ($s$, $∞$) のまま 変化しません。

2 番目の子ノードの評価値を計算した結果、ウィンドウが変化せず、2 番目以降のすべて の子ノードの ミニマックス値は $\boldsymbol{s_-}$ なので、3 番目以降のすべての子ノード も「min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)」に 分類 されます。

子ノードの分類

上記から、この分類のノードの子ノードは、以下の 2 種類に分類 されます。

分類	子ノード
min, $\boldsymbol{s}$, ($\boldsymbol{-∞}$, $\boldsymbol{∞}$)	最初の子ノード
min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)	2 番目以降の子ノード

下記は、そのことを表す図です。なお、今回の記事の図では、円はノードを表し、ノードや文字の色を以下のように色分けしました。

• max ノードは円の枠を黒色で、min ノードは赤色とした
• 円の塗りつぶしの色でノードの分類の種類を区別できるようにした
• 右に表記するノードの図形の説明では、$s_-$ の背景色を黄色で、$s_+$ の背景色を水色で表記して区別できるようにした

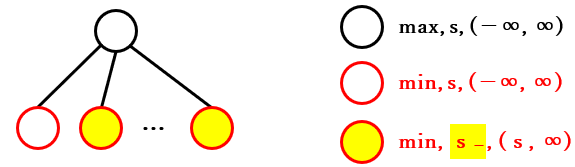
「max, $s$, ($-∞$, $∞$)」の子ノードは 2 種類に分類されることがわかったので、それらの分類のノードで行なわれる処理を検証します。

min, s, (-∞, ∞) のノードで行なわれる処理

勘の良い方は、この分類のノードで行われる処理は、先程 の「max, $s$, ($-∞$, $∞$)」と 同様である ことがわかり、以下の説明が冗長だと感じるかもしれません。そのような人は、子ノードの分類まで説明を読み飛ばしてください。

この分類のノードは min ノードで、そのミニマックス値は $s$ なので、子ノードの評価値の最小値 は $\boldsymbol{s}$ となります。

完璧な move ordering では、min ノードの 先頭の子ノードのミニマックス値 は最小値である $\boldsymbol{s}$ となり、それ以外の子ノードのミニマックス値 は $\boldsymbol{s}$ 以上、すなわち $\boldsymbol{s_+}$ となります。

最初の子ノードの計算処理

この分類のノードの 最初の子ノード は以下のように計算されるので「max, $\boldsymbol{s}$, ($\boldsymbol{-∞}$, $\boldsymbol{∞}$)」に 分類 されます。

• max ノードである
• このノードのウィンドウが受け継がれるのでウィンドウは ($-∞$, $∞$) となる
• ミニマックス値は $s$ である

また、最初の子ノードの評価値として $s$ が計算されるので、β 値 は ∞ から $\boldsymbol{s}$ に更新 され、次の子ノードの評価値を計算する際の ウィンドウが ($\boldsymbol{―∞}$, $\boldsymbol{s}$) となります。

2 番目以降の子ノードの計算処理

この分類の 2 番目の子ノードは以下のように計算されるので「max, $\boldsymbol{s_+}$, ($\boldsymbol{-∞}$, $\boldsymbol{s}$)」に 分類 されます。

• max ノードである
• ウィンドウは ($-∞$, $s$) である
• ミニマックス値は $s_+$ である

$s ≦ s_+$ なので、β 値 は $s$ のまま 更新されません。従って、次の子ノードの評価値を計算する際の ウィンドウ は ($-∞$, $s$) のまま 変化しません。

2 番目の子ノードの評価値を計算した結果、ウィンドウが変化せず、2 番目以降のすべての子ノードのミニマックス値 は $\boldsymbol{s_+}$ なので、3 番目以降のすべての子ノード も「max, $\boldsymbol{s_+}$, ($\boldsymbol{-∞}$, $\boldsymbol{s}$)」に 分類 されます。

子ノードの分類

上記から、この分類のノードの子ノードは、以下の 2 種類に分類 されます。

分類	子ノード
max, $\boldsymbol{s}$, ($\boldsymbol{-∞}$, $\boldsymbol{∞}$)	最初の子ノード
max, $\boldsymbol{s_+}$, ($\boldsymbol{-∞}$, $\boldsymbol{s}$)	2 番目以降の子ノード

下記は、そのことを表す図です。

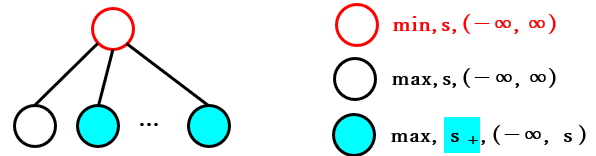
「min, $s$, ($-∞$, $∞$)」の子ノードは上記の 2 種類に分類されることがわかりましたが、そのうちの一つは先程検証 した「max, $s$, ($-∞$, $∞$)」です。従って、$N$ から 先頭の子ノードを順番にたどる と「max, $s$, ($-∞$, $∞$)」と「min, $s$, ($-∞$, $∞$)」に分類されるノードが、下図のように 繰り返される ことになります。なお、下図の黄色と水色のノードはまだ検証していないので、それらの子孫ノードは省略しています。

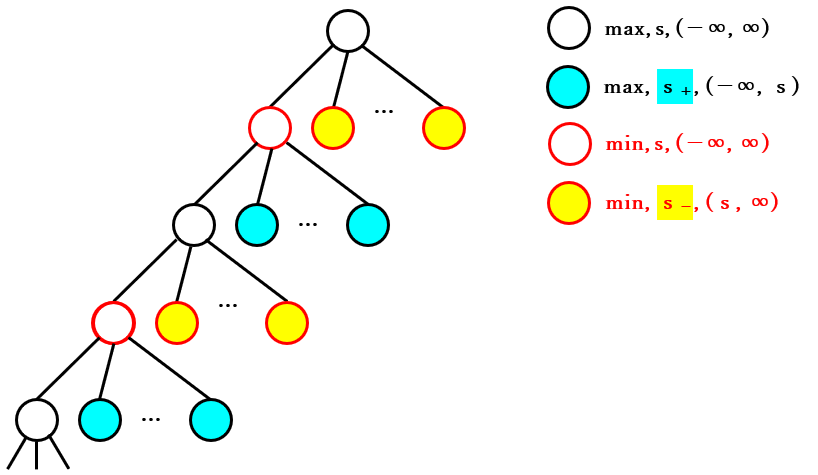
次に、まだ検証していない黄色の「min, $s_-$, ($s$, $∞$)」と、水色の「max, $s_+$, ($-∞$, $s$)」の分類のノードについて順番に検証します。

min, s-, (s, ∞) のノードで行なわれる処理

この分類のノードは min ノード で、その ミニマックス値 は $\boldsymbol{s_-}$ です。

最初の子ノードの計算処理

完璧な move ordering によって 最初の子ノードのミニマックス値 は $\boldsymbol{s_-}$ となり、この分類のノードの最初の子ノードは以下のように計算されるので「max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)」に 分類 されます。

• max ノードである
• このノードのウィンドウが受け継がれるのでウィンドウは ($s$, $∞$) となる
• ミニマックス値は $s_-$ である

ウィンドウが ($s$, $∞$) で、最初の子ノードのミニマックス値である $s_-$ は、$\boldsymbol{s_- ≦ s}$ なので、最初の子ノードで計算される評価値 は fail low の範囲 になります。min ノード では fail low が計算された場合は α 狩りが行なわれ て残りの子ノードの処理は省略されるので、この分類のノードは 最初の子ノードのみが計算 されます。

子ノードの分類

上記から、この分類のノードの子ノードは、以下の 2 種類に分類され、その中で 計算が行なわれるノードは 1 種類のみ となります。

分類	子ノード
max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)	最初の子ノード
枝狩りが行われて計算されない	2 番目以降のノード

下記はそのことを表す図です。

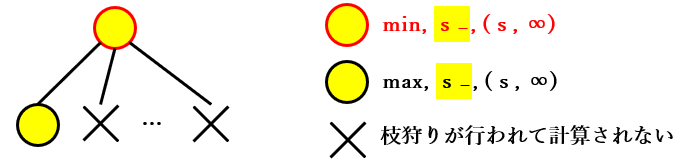
次に上記の表の「max, $s_-$, ($s$, $∞$)」の分類の検証を行います。

max, s-, (s, ∞) のノードで行なわれる処理

この分類のノードは max ノード で、そのミニマックス値は $\boldsymbol{s_-}$ なので、move ordering の有無に関わらず、すべての子ノードのミニマックス値 は $\boldsymbol{s_-}$ となります。

最初の子ノードの計算処理

この分類のノードの 最初の子ノード は、以下のように計算されるので「min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)」に 分類 されます。

• min ノードである
• このノードのウィンドウが受け継がれるのでウィンドウは ($s$, $∞$) となる
• ミニマックス値は $s_-$ である

計算されたミニマックス値は $s_-$ で $\boldsymbol{s_- ≦ s}$ なので、α 値 は $s$ のまま 更新されません。従って、次の子ノードの評価値を計算する際の ウィンドウ は ($s$, $∞$) のまま 変化しません。

2 番目以降の子ノードの計算処理

最初の子ノードの評価値を計算した結果、ウィンドウ が ($s$, $∞$) から 変化せず、すべての子ノードのミニマックス値 は $\boldsymbol{s_-}$ なので、2 番目以降のすべての子ノード も「min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)」に 分類 されます。

子ノードの分類

上記から、この分類のノードの子ノードは、以下の 1 種類のみに分類 されます。

分類	子ノード
min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)	すべての子ノード

下記は、そのことを表す図です。

「min, $s_-$, ($s$, $∞$)」の分類のノードは 既に検証済み です。その 検証結果を組み合わせる と以下のようになり、2 種類の分類のノードが繰り返される ことがわかります。

• 「min, $s_-$, ($s$, $∞$)」の子ノードは 最初の子ノードのみが計算 され、その分類は「max, $s_-$, ($s$, $∞$)」である
• 「max, $s_-$, ($s$, $∞$)」の すべての子ノードの分類 は「min, $s_-$, ($s$, $∞$)」に 戻る

下記はそのことを表す図です。

max, s+, (-∞, s) のノードで行なわれる処理

勘の良い方はこの分類のノードでは、先程の「min, $s_-$, ($s$, $∞$)」と 同様の処理が行われる ことに気づくのではないかと思います。その場合はこの後のノードの分類のまとめの所まで読み飛ばしてください。

この分類のノードは max ノードで、そのミニマックス値は $\boldsymbol{s_+}$ です。

最初の子ノードの計算処理

完璧な move ordering では最初の子ノードの評価値は $\boldsymbol{s_+}$ となり、この分類のノードの最初の子ノードは以下のように計算されるので「min, $\boldsymbol{s_+}$, ($\boldsymbol{-∞}$, $\boldsymbol{s}$)」に 分類 されます。

• min ノードである
• このノードのウィンドウが受け継がれるのでウィンドウは ($-∞$, $s$) となる
• ミニマックス値は $s_+$ である

ウィンドウが ($-∞$, $s$) で、最初の子ノードのミニマックス値 である $s_+$ は、$\boldsymbol{s ≦ s_+}$ なので、最初の子ノードで計算される評価値 は fail high の範囲 になります。max ノード では fail high が計算された場合は β 狩りが行なわれ て残りの子ノードの処理は省略されるので、この分類のノードは 最初の子ノードのみが計算されます。

子ノードの分類

上記から、この分類の子ノードは以下の 2 種類に分類され、その中で 計算が行なわれるノードは 1 種類のみ となります。

分類	子ノード
min, $\boldsymbol{s_+}$, ($\boldsymbol{-∞}$, $\boldsymbol{s}$)	最初の子ノード
枝狩りが行われて計算されない	2 番目以降のノード

下記はそのことを表す図です。

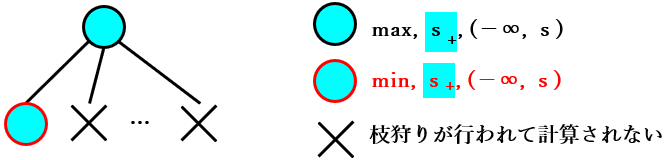
次に上記の表の「min, $s_+$, ($-∞$, $s$)」の分類の検証を行います。

min, s+, (-∞, s) のノードで行なわれる処理

この分類のノードは max ノード で、そのミニマックス値は $\boldsymbol{s_+}$ なので、move ordering の精度に関わらず、すべての子ノードのミニマックス値 は $\boldsymbol{s_+}$ となります。

最初の子ノードの計算処理

この分類のノードの 最初の子ノード は以下のように計算されるので「max, $\boldsymbol{s_+}$, ($\boldsymbol{-∞}$, $\boldsymbol{s}$)」に分類されます。

• max ノードである
• このノードのウィンドウが受け継がれるのでウィンドウは「($-∞$, $s$)」となる
• ミニマックス値は $s_+$ である

計算されたミニマックス値は $s_+$ で $\boldsymbol{s ≦ s_+}$なので、β 値 は $s$ のまま 更新されない ので、次の子ノードの評価値を計算する際の ウィンドウ は ($-∞$, $s$) のまま 変化しません。

2 番目以降の子ノードの計算処理

最初の子ノードの評価値を計算した結果、ウィンドウ が 変化せず、すべての子ノードのミニマックス値 は $\boldsymbol{s_+}$ なので、2 番目以降のすべての子ノード も「max, $\boldsymbol{s_+}$, ($\boldsymbol{-∞}$, $\boldsymbol{s}$)」に 分類 されます。

子ノードの分類

上記から、この分類のノードの子ノードは、以下の __ 1 種類のみに分類__ されます。

分類	子ノード
max, $\boldsymbol{s_+}$, ($\boldsymbol{-∞}$, $\boldsymbol{s}$)	すべての子ノード

下記は、そのことを表す図です。

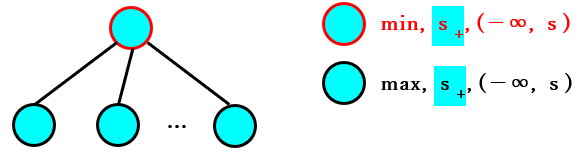
「max, $s_+$, ($-∞$, $s$)」の分類のノードは 既に検証済み です。その 検証結果を組み合わせる と以下のようになり、2 種類の分類のノードが繰り返される ことがわかります。

• 「max, $s_+$, ($-∞$, $s$)」の子ノードは 最初の子ノードのみが計算 され、その分類は「min, $s_+$, ($-∞$, $s$)」である
• 「min, $s_+$, ($-∞$, $s$)」の すべての子ノードの分類 は「max, $s_+$, ($-∞$, $s$)」に 戻る

下記はそのことを表す図です。

以上で αβ 法で計算されるノードの分類をすべて検証することができました。

ノードの分類のまとめ

完璧な move ordering での αβ 法 では、評価値が計算される ノードは 6 種類に分類 され、下記の表のように それぞれの子ノードが分類 されます。

番号	分類	最初の子ノードの番号	2 番目以降の子ノードの番号
①	max, $s$, ($-∞$, $∞$)	②	③
②	min, $s$, ($-∞$, $∞$)	①	⑤
③	min, $s_-$, ($s$, $∞$)	④	枝狩りされるので存在しない
④	max, $s_-$, ($s$, $∞$)	③	③
⑤	max, $s_+$, ($-∞$, $s$)	⑥	枝狩りされるので存在しない
⑥	min, $s_+$, ($-∞$, $s$)	⑤	⑤

また、それぞれの分類のノードの 子孫ノードの分類 は以下のように 繰り返されます。

	繰り返しの法則
$\boldsymbol{N}$ から先頭の子ノードのみを辿った子孫ノード	① → ② → ① → ② の 繰り返し
① の 2 番目以降の子ノードの子孫ノード	③ → ④ → ③ → ④ の繰り返し ③ → ④ は先頭の子ノードのみ ④ → ③ はすべての子ノード
② の 2 番目以降の子ノードの子孫ノード	⑤ → ⑥ → ⑤ → ⑥ の繰り返し ⑤ → ⑥ は先頭の子ノードのみ ⑥ → ⑤ はすべての子ノード

下記は上記の繰り返しを図示したものです。わかりやすいようにノードの円の中に分類の番号を入れました。

① → ② → ① → ② の 繰り返しの図

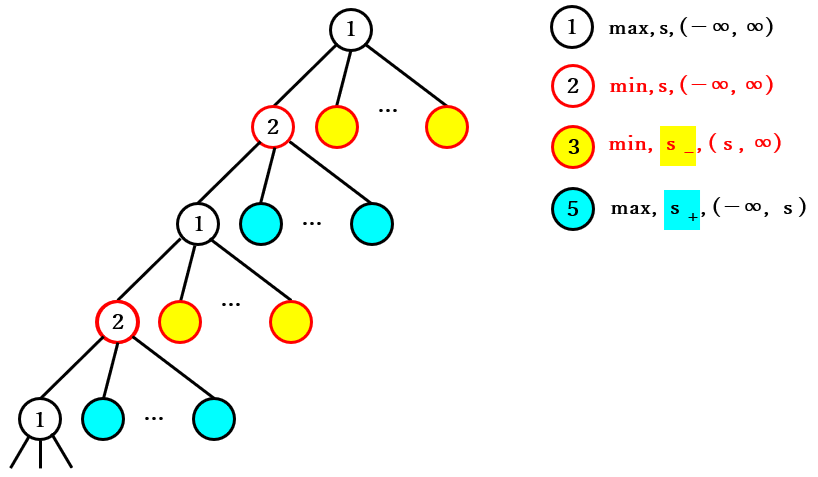
③ → ④ → ③ → ④ の繰り返しの図

⑤ → ⑥ → ⑤ → ⑥ の繰り返しの図

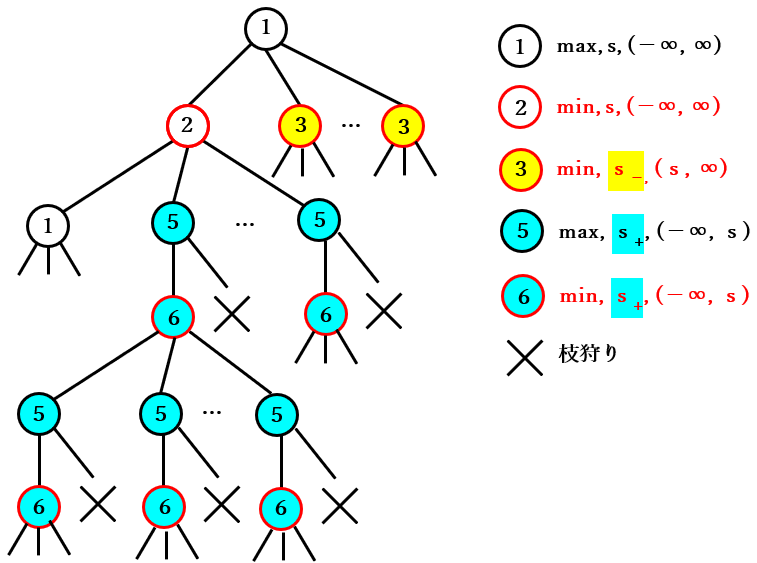
Mbtree_Anim での確認

上記の検証結果の処理が行われること を、下記のプログラムで 完璧な move ordering が行なわれた 〇× ゲームのゲーム木 に対して αβ 法で評価値を計算した結果を Mbtree_Anim で表示することで確認 することにします。

• 3 行目：ファイルからゲーム木のデータを読み込む
• 4 行目：以前の記事で定義した move_bestmove_to_head メソッドを利用して完璧な move ordering を行う
• 5 行目：Mbtree_Anim で視覚化を行えるように calc_score_for_anim で αβ 法での計算を行う
• 6 行目：Mbtree_Anim で視覚化を行う

1  from tree import Mbtree, Mbtree_Anim
2
3  mbtree = Mbtree.load("../data/abtree_root")
4  mbtree.move_bestmove_to_head()
5  mbtree.calc_score_for_anim(mbtree.root, minimax=False)
6  Mbtree_Anim(mbtree, isscore=True)

行番号のないプログラム

from tree import Mbtree, Mbtree_Anim

mbtree = Mbtree.load("../data/abtree_root")
mbtree.move_bestmove_to_head()
mbtree.calc_score_for_anim(mbtree.root, minimax=False)
Mbtree_Anim(mbtree, isscore=True)

検証を行うノード

検証を行うのは、〇× ゲームのゲーム木の 下図の数字が表示されているノード で、この番号は先程の表の分類番号に対応しています。なお、1 はゲーム開始時の局面のノードです。

〇×ゲームの ゲーム開始時の局面 は引き分けの局面なので、その ミニマックス値は 0 です。そのため、図のそれぞれの番号のノードの ミニマックス値、ウィンドウ、計算される子ノード は以下のようになります。

番号	ミニマックス値	ウィンドウ	計算される子ノード
1	0	($-∞$, $∞$)	すべて
2	0	($-∞$, $∞$)	すべて
3	0 以下	($0$, $∞$)	最初の子ノードのみ
4	0 以下	($0$, $∞$)	すべて
5	0 以上	($-∞$, $0$)	最初の子ノードのみ
6	0 以上	($-∞$, $0$)	すべて

下記はそれぞれの番号のノードの 計算を開始する start のフレーム と 評価値が確定した end のフレームです。start のフレームには ウィンドウ が、end のフレームには score に計算された評価値 と、計算が行われた子ノードが明るい色で表示 されます。

1 のノード。左図のウィンドウが ($-∞$, $∞$)、右図の評価値が 0、すべての子ノードの評価値が計算されていることから、検証したとおりの計算が行われていることが確認できます。

　

2 のノード。左図のウィンドウが ($-∞$, $∞$)、右図の評価値が 0、すべての子ノードの評価値が計算されていることから、検証したとおりの計算が行われていることが確認できます。

　

3 のノード。左図のウィンドウが ($0$, $∞$)、右図の評価値が 0 で 0 以下、最初の子ノードのみが計算されていることから、検証したとおりの計算が行われていることが確認できます。

　

4 のノード。左図のウィンドウが ($0$, $∞$)、右図の評価値が 0 で 0 以下、すべての子ノードの評価値が計算されていることから、検証したとおりの計算が行われていることが確認できます。

　

5 のノード。左図のウィンドウが ($-∞$, $0$)、右図の評価値が 1 で 0 以上、最初の子ノードのみが計算されていることから、検証したとおりの計算が行われていることが確認できます。

　

6 のノード。左図のウィンドウが ($-∞$, $0$)、右図の評価値が 1 で 0 以上、すべての子ノードの評価値が計算されていることから、検証したとおりの計算が行われていることが確認できます。

　

長くなるので本記事での検証はここまでにします。興味がある方は様々な操作を行い、1 と 2 が繰り返されるなど、他のノードでも検証した処理が行われることを確認してみて下さい。

完璧な move ordering でのスカウト法で行なわれる処理

次に、完璧な move ordering での スカウト法で行なわれる処理 を、αβ 法と同様の方法で検証します。

max, s, (-∞, ∞) のノードで行なわれる処理

αβ 法の場合と同様に、$\boldsymbol{N}$ は「max, $\boldsymbol{s}$, ($\boldsymbol{-∞}$, $\boldsymbol{∞}$)」に 分類 されます。

最初の子ノードの計算処理

スカウト法 では、最初の子ノード の計算処理は αβ 法と同じ方法で行う ため、この分類のノードの 最初の子ノード は αβ 法の場合と同様に「min, $\boldsymbol{s}$, ($\boldsymbol{-∞}$, $\boldsymbol{∞}$)」に分類されます。

また、以下の性質は αβ 法の場合と同様です。

• α 値 が $\boldsymbol{s}$ に更新 される
• 完璧な move ordering の結果、2 番目以降の子ノードのミニマックス値 は $\boldsymbol{s_-}$ になる

2 番目以降の子ノードの計算処理

スカウト法 では 2 番目以降の子ノード は (α 値, α 値 + 1) というウィンドウの null window search で計算 されます。従って、この分類のノードの 2 番目の子ノード は、以下のように計算されるので「min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)」に分類されます。

• min ノードである
• ウィンドウは ($s$, $s + 1$) となる
• ミニマックス値は $s_-$ である

$\boldsymbol{s_- ≦ s}$ なので、α 値 は $s$ のまま 更新されません。従って、次の子ノードの評価値を計算する際の ウィンドウ は ($s$, $s + 1$) のまま 変化しません。また、ミニマックス値は fail low の範囲なので αβ 法と同じウィンドウで計算をやり直す必要はありません¹。

2 番目の子ノードの評価値を計算した結果、ウィンドウが変化せず、2 番目以降のすべての子ノードのミニマックス値は $s_-$ なので、3 番目以降のすべての子ノード も「min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)」に 分類 されます。

子ノードの分類

上記から、「max, $s$, ($-∞$, $∞$)」に分類されるノードの子ノードは、以下の 2 種類に分類 されます。比較できるように、αβ 法の場合の分類も表に入れました。

スカウト法の場合の分類	αβ 法の場合の分類	子ノード
min, $\boldsymbol{s}$, ($\boldsymbol{-∞}$, $\boldsymbol{∞}$)	スカウト法と同じ	最初の子ノード
min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)	min, $s_-$, ($s$, $∞$)	2 番目以降の子ノード

上記から、αβ 法との違い は 2 番目以降の子ノード の ウィンドウだけ であることがわかります。従って、このことを表す図は αβ 法の場合とほぼ同じになるので省略します。

min, s, (-∞, ∞) のノードで行なわれる処理

同じような分析を何度も繰り返すのは冗長なので、この分類のノードで行なわれる処理は 結果のみを示します。余裕がある方はこれまでと同様の手順で下記のような結果になることを確認して下さい。

「min, $s$, ($-∞$, $∞$)」に分類されるノードの子ノードは、以下の 2 種類に分類 されます。

スカウト法の場合の分類	αβ 法の場合の分類	子ノード
max, $\boldsymbol{s}$, ($\boldsymbol{-∞}$, $\boldsymbol{∞}$)	スカウト法と同じ	最初の子ノード
max, $\boldsymbol{s_+}$, ($\boldsymbol{s-1}$, $\boldsymbol{s}$)	max, $s_+$, ($-∞$, $s$)	2 番目以降の子ノード

上記から、スカウト法 でも αβ 法と同様 に、$N$ から 先頭の子ノードを順番にたどる と、「max, $s$, ($-∞$, $∞$)」と「min, $s$, ($-∞$, $∞$)」に分類されるノードが、下図のように 繰り返される ことになります。その下の αβ 法の場合の図と比較して、ここまでに検証した範囲では、αβ 法同じノードの処理が行われる ことを確認して下さい。なお、下図では αβ 法と異なる部分を緑色の背景色で塗りつぶしました。

スカウト法の場合の図

αβ 法の場合の図

min, s-, (s, s + 1) のノードで行なわれる処理

この分類のノードは min ノード で、その ミニマックス値は $\boldsymbol{s_-}$ です。

最初の子ノードの計算処理

完璧な move ordering では 最初の子ノードの評価値 は $\boldsymbol{s_-}$ となり、この分類のノードの 最初の子ノード は以下のように計算されるので「max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)」に分類されます。

• max ノードである
• このノードのウィンドウが受け継がれるのでウィンドウは ($s$, $s + 1$) となる
• ミニマックス値は $s_-$ である

ウィンドウが ($s$, $s + 1$) で、最初の子ノードのミニマックス値である $s_-$ は、$\boldsymbol{s_- ≦ s}$ なので、最初の子ノードのミニマックス値 は fail low の範囲 になります。min ノード では fail low が計算された場合は α 狩り が行なわれて 残りの子ノードの処理は省略 されるので、この分類のノードは 最初の子ノードのみが計算 されます。

これは、αβ 法 で「min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)」の分類のノードで 行われる処理と同じ です。

子ノードの分類

上記から、この分類のノードの子ノードは以下の 2 種類に分類され、その中で 計算が行なわれるノードは 1 種類のみ となります。比較できるように αβ 法で「min, $s_-$, ($s$, $∞$)」の分類のノードで行なわれる処理を表に入れました。

スカウト法の場合の分類	αβ 法の場合の分類	子ノード
max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)	max, $s_-$, ($s$, $∞$)	最初の子ノード
枝狩りが行われて計算されない	スカウト法と同じ	2 番目以降のノード

従って、この分類のノードで行なわれる処理は、αβ 法 で「min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)」の分類のノードで行なわれる処理と 同じ構造になる ことがわかりました。

max, s-, (s, s + 1) のノードで行なわれる処理

この分類のノードは max ノード で、そのミニマックス値は $s_-$ なので、move ordering の有無に関わらず、すべての子ノードのミニマックス値 は $\boldsymbol{s_-}$ となります。

最初の子ノードの計算処理

この分類のノードの最初の子ノードは以下のように計算されるので「min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)」に分類されます。

• min ノードである
• このノードのウィンドウが受け継がれるのでウィンドウは ($s$, $s + 1$) となる
• ミニマックス値は $s_-$ である

計算されたミニマックス値は $s_-$ で $\boldsymbol{s_- ≦ s}$ なので、α 値 は $s$ のまま 更新されません。従って、次の子ノード の評価値を計算する際の ウィンドウ は 変化しません。

2 番目以降の子ノードの計算処理

最初の子ノードの評価値を計算した結果、ウィンドウが ($s$, $s + 1$) から変化せず、すべての子ノードのミニマックス値は $s_-$ なので、2 番目以降のすべての子ノード も「min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)」に 分類 されます。

子ノードの分類

上記から、この分類の子ノードは、以下の 1 種類のみに分類 されます。比較できるように αβ 法で「max, $s_-$, ($s$, $∞$)」の分類のノードで行なわれる処理を表に入れました。

スカウト法の場合の分類	αβ 法の場合の分類	子ノード
min, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)	min, $s_-$, ($s$, $∞$)	すべての子ノード

従って、この分類のノードで行なわれる処理は、αβ 法 で「max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)」の分類のノードで行なわれる処理と 同じ構造になる ことがわかりました。

「min, $s_-$, ($s$, $s + 1$)」の分類のノードは既に 検証済み です。その 検証結果を組み合わせる と以下のようになり、2 種類の分類のノードが繰り返される ことがわかります。

• 「min, $s_-$, ($s$, $s + 1$)」の子ノードは 最初の子ノードのみが計算 され、その分類は「max, $s_-$, ($s$, $s + 1$)」である
• 「max, $s_-$, ($s$, $s + 1$)」の すべての子ノードの分類 は「min, $s_-$, ($s$, $s + 1$)」に 戻る

下図はそのことを表す図です。その下の αβ 法の場合の図と同じ処理が行われる ことを確認して下さい。

スカウト法の場合の図

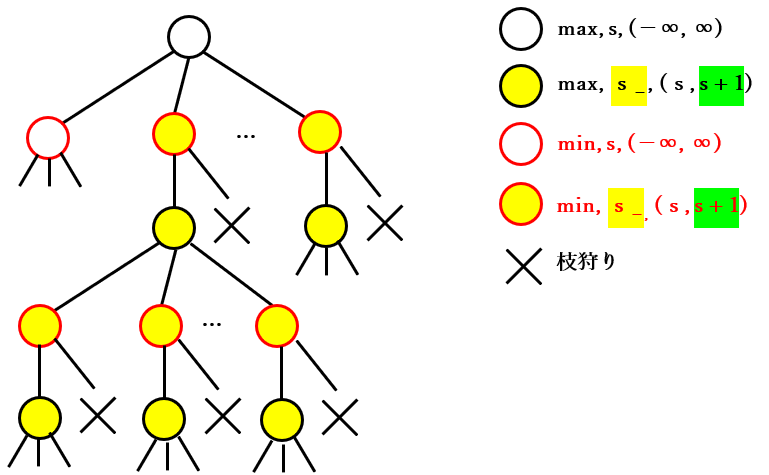
αβ 法の場合の図

残りの分類のノードで行なわれる処理

説明はこれまでと同様なので省略しますが、「max, $\boldsymbol{s_+}$, ($\boldsymbol{s - 1}$, $\boldsymbol{s}$)」に分類されるノードの子ノードは以下の 2 種類に分類され、その中で 計算が行なわれるノードは 1 種類のみ となります。

スカウト法の場合の分類	αβ 法の場合の分類	子ノード
min, $\boldsymbol{s_+}$, ($\boldsymbol{s - 1}$, $\boldsymbol{s}$)	min, $s_+$, ($-∞$, $s$)	最初の子ノード
枝狩りが行われて計算されない	スカウト法と同じ	2 番目以降のノード

残りの「min, $\boldsymbol{s_+}$, ($\boldsymbol{s-1}$, $\boldsymbol{s}$)」に分類されるノードの子ノードは、以下の 1 種類のみに分類 されます。

スカウト法の場合の分類	αβ 法の場合の分類	子ノード
max, $\boldsymbol{s_+}$, ($\boldsymbol{s-1}$, $\boldsymbol{s}$)	max, $s_+$, ($-∞$, $s$)	すべての子ノード

上記の 検証結果を組み合わせる 先程と同様に 2 種類の分類のノードが繰り返される ことがわかります。下図はそのことを表す図です。その下の αβ 法の場合の図と同じ処理が行われる ことを確認して下さい。

スカウト法の場合の図

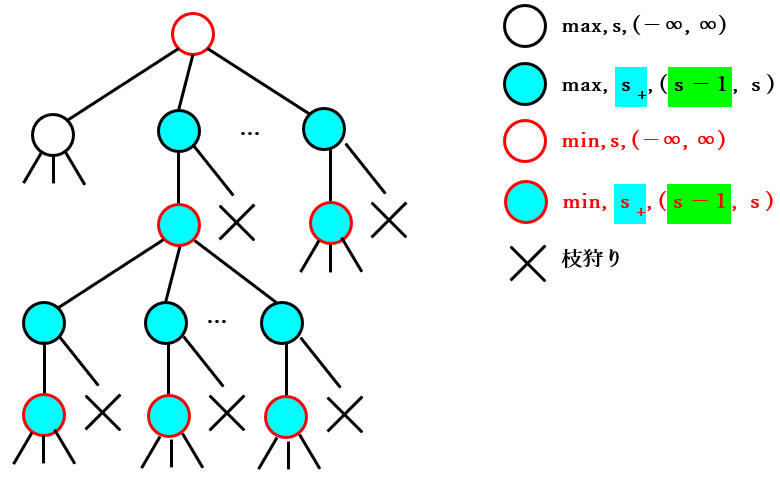
αβ 法の場合の図

以上でスカウト法で計算されるノードの分類をすべて検証することができました。

スカウト法と αβ 法で行なわれる処理の比較

下記は 完璧な move ordering でスカウト法と αβ 法の ノードの分類 を まとめた表 で、スカウト法と αβ 法では どちらもノードが 6 種類に分類 されます。また、先ほど行った検証から、どちらも 対応する分類で同じ子ノードの処理が行われる ことが確認できたことから、同じノードが同じ番号に分類 されます。

なお、番号1 は 最初の子ノードの番号 、番号2 は 2 番目以降の子ノードの番号 を表します。

番号	スカウト法での分類	αβ 法での分類	番号1	番号2
①	max, $s$, ($-∞$, $∞$)	スカウト法と同じ	②	③
②	min, $s$, ($-∞$, $∞$)	スカウト法と同じ	①	⑤
③	min, $s_-$, ($s$, $s + 1$)	min, $s_-$, ($s$, $∞$)	④	枝狩り
④	max, $s_-$, ($s$, $s + 1$)	max, $s_-$, ($s$, $∞$)	③	③
⑤	max, $s_+$, ($s-1$, $s$)	max, $s_+$, ($-∞$, $s$)	⑥	枝狩り
⑥	min, $s_+$, ($s-1$, $s$)	min, $s_+$, ($-∞$, $s$)	⑤	⑤

また、それぞれの分類のノードの 子孫ノードの分類 は、スカウト法と αβ 法で以下のように 全く同じ法則の繰り返し が行なわれます。

	繰り返しの法則
$\boldsymbol{N}$ から先頭の子ノードのみを辿った子孫ノード	① → ② → ① → ② の 繰り返し
① の 2 番目以降の子ノードの子孫ノード	③ → ④ → ③ → ④ の繰り返し ③ → ④ は先頭の子ノードのみ ④ → ③ はすべての子ノード
② の 2 番目以降の子ノードの子孫ノード	⑤ → ⑥ → ⑤ → ⑥ の繰り返し ⑤ → ⑥ は先頭の子ノードのみ ⑥ → ⑤ はすべての子ノード

上記を言葉で説明すると以下のようになります。

• ウィンドウが ($-∞$, $∞$) の 最初の子ノード は、αβ 法でもスカウト法でも 同じ ($―∞$, $∞$) のウィンドウ で $\boldsymbol{s}$ という ミニマックス値が計算 される
• max ノード で ウィンドウが ($-∞$, $∞$) のノードの 2 番目以降の子孫ノード では、以下のような計算が行われる
  • すべての子孫ノード で、αβ 法 では ($\boldsymbol{s}$, $\boldsymbol{∞}$)、スカウト法 では ($\boldsymbol{s}$, $\boldsymbol{s + 1}$) というウィンドウで計算がおこなわれる
  • すべての子孫ノード で、ミニマックス値 が $\boldsymbol{s_-}$ であることが計算される
  • 子孫ノードの中の max ノード では、すべての子ノードのミニマックス値 が fail low となるので、すべての子ノードの評価値の計算が行なわれる
  • 子孫ノードの中の min ノード では、move ordering によって 最初の子ノードのミニマックス値が fail low の $\boldsymbol{s_-}$ となるため、いずれの場合も α 狩り が行なわれ 2 番目以降の子ノードは計算されない
• max ノード で ウィンドウが ($-∞$, $∞$) のノードの 2 番目以降の子孫ノード の場合も、上記と同様の計算 が行われる

上記から、完璧な move ordering が行われる場合は、スカウト法と αβ 法で まったく同じノードの計算が行なわれる ことが確認できました。従って 完璧な move ordering が行われる場合は、スカウト法と αβ 法の効率は全く同じ になります。

スカウト法によって行なわれる効率化

スカウト法 が、どのような場合に αβ 法よりも効率が高くなるか についてピンと来ない人がいるかもしれないので、スカウト法の方が αβ 法よりも 効率が良くなる場合の具体例 を紹介します。これは 一例にすぎない ので、他にも効率が良くなる場合があります。余裕がある方はそのような場合を探してみて下さい。

下記の条件 で $N$ の評価値を計算すると、スカウト法の方が αβ 法よりも 枝狩りが多く行われるため、効率が高く なります。

• 評価値は整数のみが計算されるものとする
• $N$ の 2 番目の子ノードを $C$ と表記する
• $C$ の $i$ 番目の子ノードを $G_i$² と表記する
• $\boldsymbol{C}$ の子ノードのみ move ordering が正しく行われず、最初の子ノード $\boldsymbol{G_1}$ の ミニマックス値 が $\boldsymbol{s}$ より大きな値 になる。以後は $s$ より大きな値 を $\boldsymbol{s_>}$ と表記³する
• $C$ の 2 番目の子ノード $\boldsymbol{G_2}$ の ミニマックス値 が $\boldsymbol{s_-}$（$s$ 以下）になる

下図は上記のゲーム木の一部を図示したものです。$C$ の子ノードの数は 2 以上であれば何でも構いません。下図では $C$ に $n$ 個の子ノードが存在するものとして図示しました。また、$C$ の子ノードは move ordering が正しく行われていないので、その 分類はまだ検証されていません。そのことを表すため $C$ の子ノードを 紫色で塗りつぶしました。

$\boldsymbol{C}$ 以外 のノードでは 完璧な move ordering が行われるので、$\boldsymbol{C}$ 以外 の $N$ の子ノードの 計算の効率 は αβ 法とスカウト法で同じ になります。従って、$\boldsymbol{C}$ の評価値の計算の 効率の差 が、$N$ の評価値を計算した際の αβ 法とスカウト法の効率の差 になります。

αβ 法でのノード C の計算処理

まず、αβ 法 でのノード $\boldsymbol{C}$ の計算処理 を検証します。

$\boldsymbol{N}$ の 子ノードは完璧な move ordering が行われており、$C$ は $N$ の 2 番目の子ノードなので、$C$ を計算する際の ウィンドウ は先程検証した際と同様に ($\boldsymbol{s}$, $\boldsymbol{∞}$) となります。

最初の子ノードの計算処理

この分類のノードの最初の子ノードは以下のように計算されるので「max, $\boldsymbol{s_>}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)」に 分類 されます。

• min ノードである
• このノードのウィンドウが受け継がれるのでウィンドウは ($s$, $∞$) となる
• ミニマックス値は $s_>$ である

計算されたミニマックス値は $s_>$ で $\boldsymbol{s < s_>}$ なので、α 狩りは行なわれません。β 値 が $∞$ から $\boldsymbol{s_>}$ に 更新される ので、次の $\boldsymbol{G_2}$ の評価値を計算する際の ウィンドウ は ($\boldsymbol{s}$, $\boldsymbol{s_>}$) に更新されます。

2 番目の子ノードの計算処理

$G_2$ のノードは、以下のように計算されるので「max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s_>}$)」に分類されます。

• min ノードである
• ウィンドウは ($s$, $s_>$) である
• ミニマックス値は $s-$ である

計算された $G_2$ のミニマックス値 $s_-$ は $\boldsymbol{s_- < s}$　なので α 狩りが行われ、残りの子ノードの評価値の計算は省略 されます。

行なわれる処理のまとめ

上記から $C$ の評価値を計算する際には下記の 2 つの子ノードの計算 が行われます。

• 「max, $\boldsymbol{s_>}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)」に分類される $G_1$
• 「max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s_>}$)」に分類される $G_2$

スカウト 法でのノード C の計算処理

次に、スカウト法 でのノード $\boldsymbol{C}$ の計算処理 を検証します。

$\boldsymbol{N}$ の 子ノードは完璧な move ordering が行われており、$C$ は $N$ の 2 番目の子ノードなので、$C$ を計算する際の ウィンドウ は先程検証した際と同様に ($\boldsymbol{s}$, $\boldsymbol{s + 1}$) となります。

最初の子ノードの計算処理

この分類のノードの最初の子ノードは以下のように計算されるので「max, $\boldsymbol{s_>}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)」に分類されます。

• min ノードである
• このノードのウィンドウが受け継がれるのでウィンドウは ($s$, $s + 1$) となる
• ミニマックス値は $s_>$ である

計算されたミニマックス値は $s_>$ で $\boldsymbol{s < s_>}$ なので、α 狩りは行なわれません。
評価値は整数のみが計算されるので、$s < s + 1 ≦ s_>$ となります。そのため、β 値 は $s + 1$ のまま更新されず、次の $\boldsymbol{G_2}$ の評価値を計算する際の ウィンドウ は ($s$, $s + 1$) のまま 更新されません。

2 番目の子ノードの計算処理

$G_2$ のノードは、以下のように計算されるので「max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)」に分類されます。

• min ノードである
• ウィンドウは ($s$, $s+1$) である
• ミニマックス値は $s-$ である

計算された $G_2$ のミニマックス値 $s_-$ は $\boldsymbol{s_- < s}$　なので α 狩りが行われ、残りの子ノードの評価値の計算は省略 されます。

行なわれる処理のまとめ

上記から $C$ の評価値を計算する際には下記の 2 つの子ノードの計算 が行われます。

• 「max, $\boldsymbol{s_>}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)」に分類される $G_1$
• 「max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s+ 1}$)」に分類される $G_2$

計算処理の比較

上記から $C$ の計算を行う際に、αβ 法とスカウト法では 下記の 2 種類の子ノードの計算処理を行う ことがわかります。

子ノード	αβ 法での分類	スカウト法での分類
$\boldsymbol{G_1}$	max, $\boldsymbol{s_>}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)	max, $\boldsymbol{s_>}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)
$\boldsymbol{G_2}$	max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s_>}$)	max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s+ 1}$)

それぞれの子ノードで行われる処理を比較します。

最初の子ノードの処理の比較

αβ 法 の場合は $G_1$ の ウィンドウ が ($\boldsymbol{s}$, $\boldsymbol{∞}$) なので、max ノード である $G_1$ の子ノードの評価値がどのような値であっても β 狩りが行われることはありません。

一方、スカウト法 の場合は以下の理由から $G_1$ の評価値を計算する際に β 狩りが行われる可能性 があります。

• $G_1$ のミニマックス値である $\boldsymbol{s_>}$ は $\boldsymbol{s + 1}$ 以上 である
• $G_1$ は max ノード なので、子ノードの中に 必ずミニマックス値が $\boldsymbol{s + 1}$ 以上 のノードが 存在する
• ウィンドウが ($s$, $s + 1$) なので、ミニマックス値が $\boldsymbol{s + 1}$ 以上 の子ノード 以降の子ノードの枝狩りが行われる。従って、そのような子ノードが 最後の子ノードでない場合 に β 狩りが行なわれる

上記から、$\boldsymbol{G_1}$ のノードの評価値を計算する場合は、スカウト法 は αβ 法以上の効率 で計算が行われます。下記はそれぞれで行われる処理を図示したものです。

αβ 法の場合

スカウト法の場合

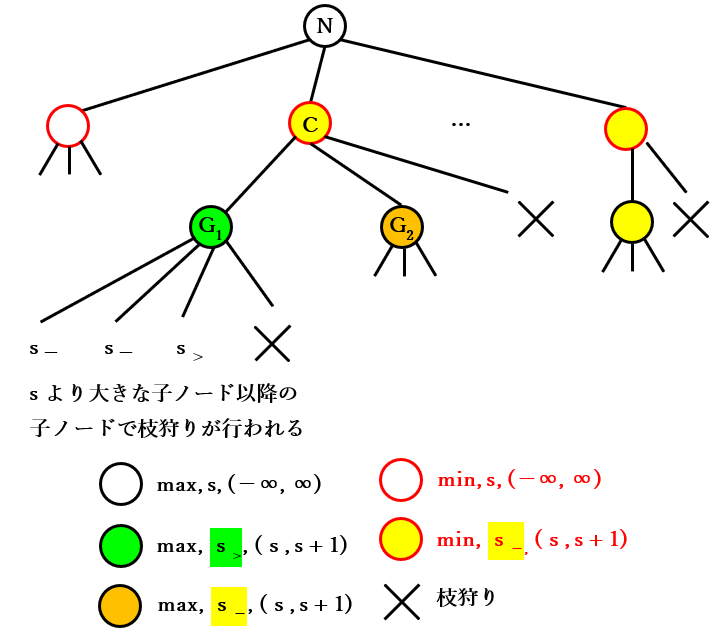
2 番目の子ノードの処理の比較

max ノードでミニマックス値が $\boldsymbol{s_-}$ の場合は、先程「max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{∞}$)」と「max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s + 1}$)」の場合で 同じ処理が行われる ことを示しました。これは、下記の条件が満たされる場合 は、すべての子ノードが fail low の範囲になる ため β 狩りが行われず、すべての子ノードの計算を行う ためです。

• max ノードである
• ミニマックス値がウィンドウの α 値以下である

「max, $\boldsymbol{s_-}$, ($\boldsymbol{s}$, $\boldsymbol{s_>}$)」の場合は その条件を満たす ので、αβ 法とスカウト法で $\boldsymbol{G_2}$ の効率は同じ になります。

上記の考察から、以下の事がわかります。

子孫ノードで move ordering が正しく行われなかった場合 に、null window search の効果によって スカウト法 が αβ 法以上の効率を得ることができる場合がある。

上記の具体例の補足

上記では、$C$ の子ノードの中で 2 番目の子ノード のミニマックス値が はじめて $\boldsymbol{s_-}$（$\boldsymbol{s}$ 以下）になる例 を示しましたが、3 番目以降 の子ノードのミニマックス値が はじめて $\boldsymbol{s_-}$ になる場合 は、それ以前のすべての子ノード の計算処理を αβ 以上の効率で行うことができる ようになります。

従って、上記の例 では、move ordering の精度が悪く、最善手の子ノードが後ろの方に配置されるほど スカウト法の 効率が αβ よりも高くなることが期待 できます。

なお、上記の例はスカウト法で null window search の計算後に αβ 法でのやり直しが行われない 場合の例です。計算のやり直しが行われる場合 は上記の例のような 単純な比較を行うことはできない 点に注意して下さい。

また、上記では 複数のノードで完璧な move ordering が行われない場合は考慮していません。興味と余裕がある方はそのような場合の比較を行ってみて下さい。

スカウト法の視覚化について

Mbtree_Anim でスカウト法の視覚化を行えるようにしようと最初は考えていたのですが、話が進まなくなるのと、それほど重要ではない気がしましたので行わないことにしました。余裕がある方は、calc_score_for_anim を修正してスカウト法の視覚化を行えるようにしてみて下さい。

今回の記事のまとめ

今回の記事では、完璧な move ordering での αβ 法とスカウト法が 同じノードの計算処理を行う ため、効率が同じになる ことを示しました。また、スカウト法の効率が αβ 法以上になる具体例を示しました。

本記事で入力したプログラム

リンク	説明
marubatsu.ipynb	本記事で入力して実行した JupyterLab のファイル

次回の記事

1. 以後は、αβ 法と同じウィンドウで計算をやり直す必要がない場合の説明を省略します ↩

2. $G$ は $N$ の孫ノードなので、孫を表す grandchild の略です ↩

3. $s$ を含まないので ${s_+}$ と表記することはできないので、このような表記にしました ↩