はじめに
2021/2/19・20に実施される日本ディープラーニング協会(JDLA)E資格合格を目指して、ラビットチャレンジを受講した際の学習記録です。
科目一覧
応用数学
機械学習
深層学習(day1)
深層学習(day2)
深層学習(day3)
深層学習(day4)
Section1:再帰型ニューラルネットワークの概念
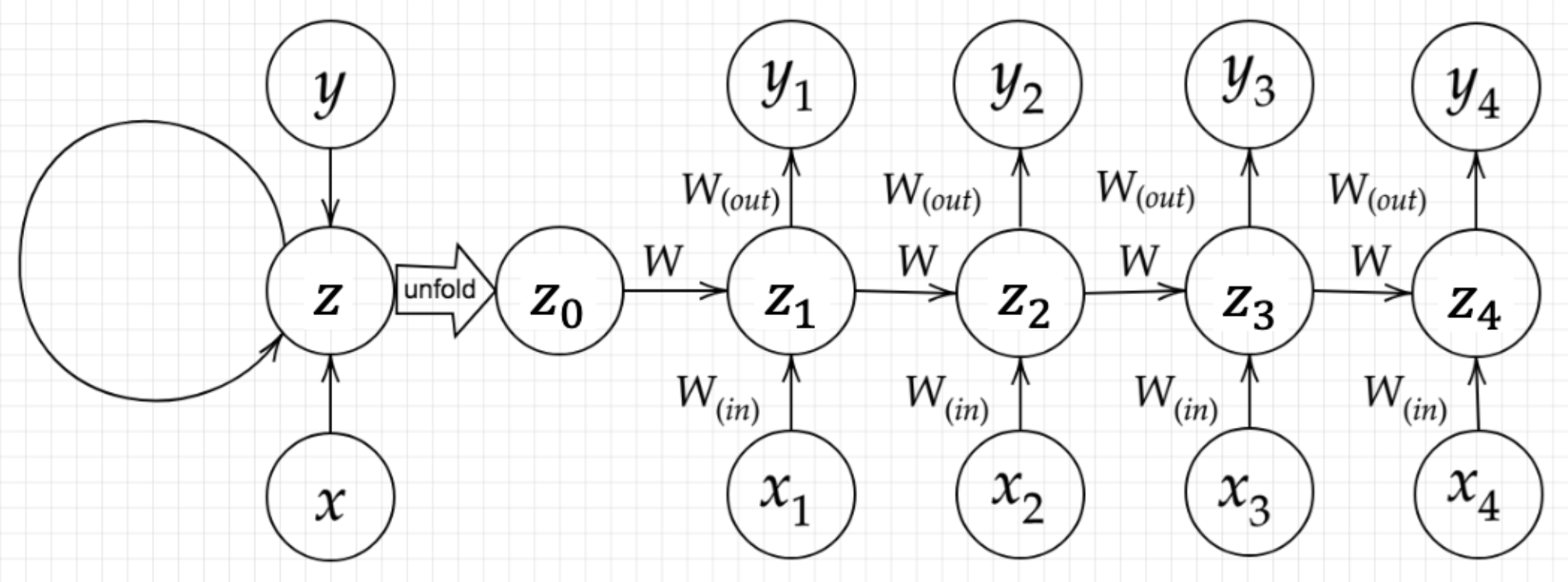
Recurrent Neural Network(RNN)とは、時系列データに対応可能なニューラルネットワークのことである。
時系列データは時間的順序を追って一定間隔ごとに観察され、しかも相互に統計的依存関係が認められるようなデータの系列のことであり、音声データやテキストデータがある。
RNNは時系列データを扱うため、初期の状態と過去の時間 $t-1$ の状態を保持し、次の時間 $t$ の状態を求める再帰的構造が必要になる。
$$ u^t = W_{(in)}x^t+Wz^{(t-1)}+b $$
$$ z^t = f(W_{(in)}x^t+Wz^{(t-1)}+b) $$
$$ v^t = W_{(out)}z^t+c $$
$$ y^t = g(W_{(out)}z^t+c) $$
RNNにおいてのパラメータ調整方法として、誤差逆伝播の一種であるBPTTがある。
【パラメータの更新式】
$$ W_{(in)}^{t+1} = W_{(in)}^{t}-\epsilon\frac{\partial E}{\partial W_{(in)}} = W_{(in)}^{t}-\epsilon \sum_{z=0}^{T_t}\delta^{t-z}[x^{t-z}]^T $$
$$ W_{(out)}^{t+1} = W_{(out)}^{t}-\epsilon\frac{\partial E}{\partial W_{(out)}} = W_{(out)}^{t}-\epsilon \delta^{out,t}[z^{t}]^T $$
$$ W^{t+1} = W^{t}-\epsilon\frac{\partial E}{\partial W} = W_{(in)}^{t}-\epsilon \sum_{z=0}^{T_t}\delta^{t-z}[x^{t-z-1}]^T $$
$$ b^{t+1} = b^t-\epsilon\frac{\partial E}{\partial b} = b^t-\epsilon \sum_{z=0}^{T_t}\delta^{t-z} $$
$$ c^{t+1} = c^t-\epsilon\frac{\partial E}{\partial c} = c^t-\epsilon \delta^{out,t} $$
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from common import functions
import matplotlib.pyplot as plt
def d_tanh(x):
return 1/(np.cosh(x) ** 2)
# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1
weight_init_std = 1
learning_rate = 0.1
iters_num = 10000
plot_interval = 100
# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)
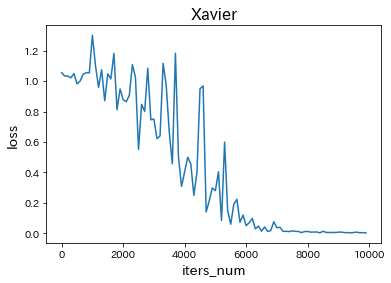
# Xavier
# W_in = np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size))
# W_out = np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size))
# W = np.random.randn(hidden_layer_size, hidden_layer_size) / (np.sqrt(hidden_layer_size))
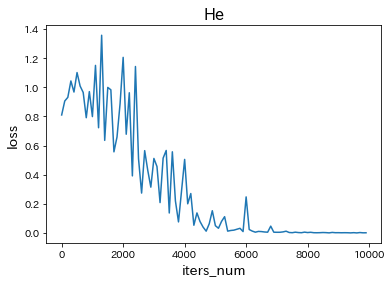
# He
# W_in = np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size)) * np.sqrt(2)
# W_out = np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size)) * np.sqrt(2)
# W = np.random.randn(hidden_layer_size, hidden_layer_size) / (np.sqrt(hidden_layer_size)) * np.sqrt(2)
# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)
u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))
delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))
all_losses = []
for i in range(iters_num):
# A, B初期化 (a + b = d)
a_int = np.random.randint(largest_number/2)
a_bin = binary[a_int] # binary encoding
b_int = np.random.randint(largest_number/2)
b_bin = binary[b_int] # binary encoding
# 正解データ
d_int = a_int + b_int
d_bin = binary[d_int]
# 出力バイナリ
out_bin = np.zeros_like(d_bin)
# 時系列全体の誤差
all_loss = 0
# 時系列ループ
for t in range(binary_dim):
# 入力値
X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1)
# 時刻tにおける正解データ
dd = np.array([d_bin[binary_dim - t - 1]])
u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
z[:,t+1] = functions.sigmoid(u[:,t+1])
# z[:,t+1] = functions.relu(u[:,t+1])
# z[:,t+1] = np.tanh(u[:,t+1])
y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))
#誤差
loss = functions.mean_squared_error(dd, y[:,t])
delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t])
all_loss += loss
out_bin[binary_dim - t - 1] = np.round(y[:,t])
for t in range(binary_dim)[::-1]:
X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1)
delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_sigmoid(u[:,t+1])
# delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_relu(u[:,t+1])
# delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * d_tanh(u[:,t+1])
# 勾配更新
W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1))
# 勾配適用
W_in -= learning_rate * W_in_grad
W_out -= learning_rate * W_out_grad
W -= learning_rate * W_grad
W_in_grad *= 0
W_out_grad *= 0
W_grad *= 0
if(i % plot_interval == 0):
all_losses.append(all_loss)
print("iters:" + str(i))
print("Loss:" + str(all_loss))
print("Pred:" + str(out_bin))
print("True:" + str(d_bin))
out_int = 0
for index,x in enumerate(reversed(out_bin)):
out_int += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
print("------------")
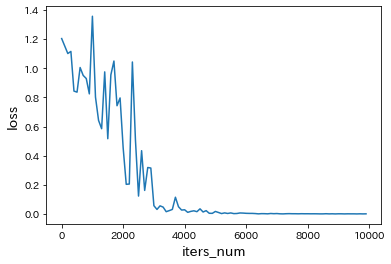
lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.xlabel("iters_num", fontsize=14)
plt.ylabel("loss", fontsize=14)
plt.show()
-
weight_init_stdを変更
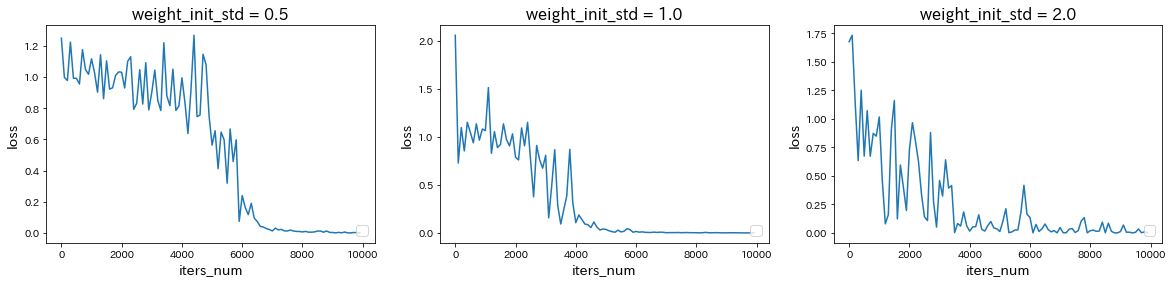
→ weight_init_stdを1.0から0.5に減少または2.0に増加させると、どちらも収束が遅くなった。 -
learning_rateを変更
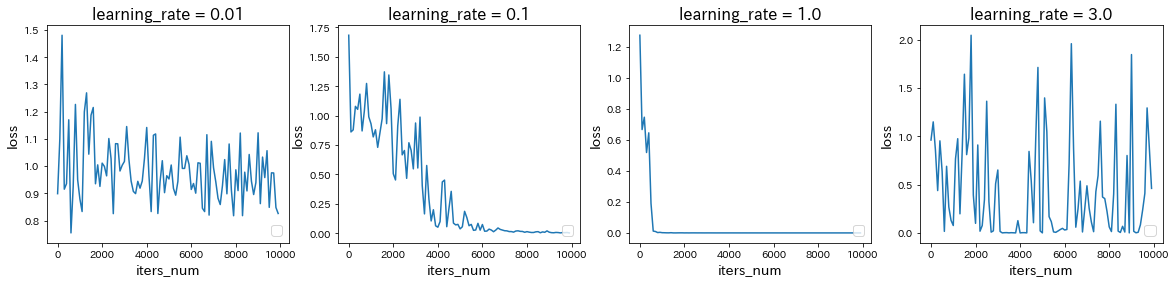
→ learning_rateを0.1から0.01に減少させると学習が遅くなったが、1.0に増加させると学習が早くなり、さらに3.0に増加させると学習が進まなかった。 -
hidden_layer_sizeを変更
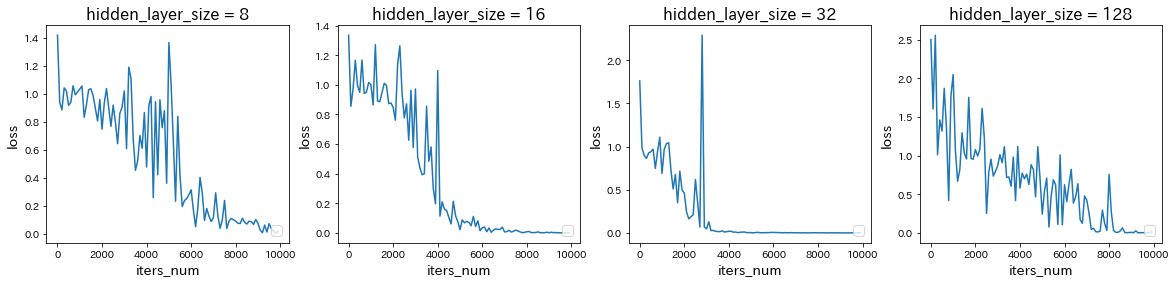
→ hidden_layer_sizeを16から8に減少させると学習が遅くなったが、32に増加させると学習が早くなり、さらに128に増加させると学習が遅くなった。 -
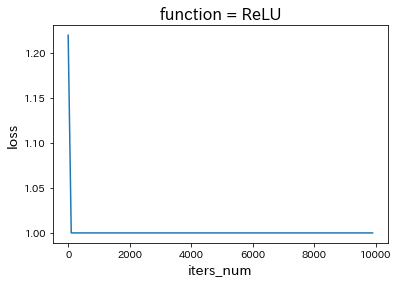
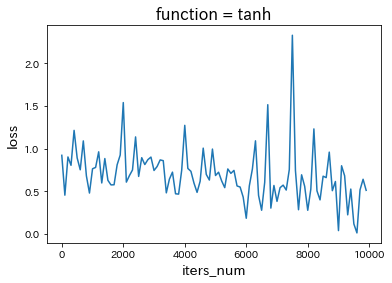
中間層の活性化関数を変更
Section2:LSTM(Long Short-Term Memory)
単純なRNNでは、誤差逆伝播を行う際の勾配消失のため、長距離依存関係を上手く学習することができない。
LSTMはその問題点を解消する手法として用いられている。
-
Input gate:$ i_t = \sigma(W^{(i)}x_t + U^{(i)}h_{t-1} + b^{(i)} ) $
-
Forget gate:$ f_t = \sigma(W^{(f)}x_t + U^{(f)}h_{t-1} + b^{(f)} ) $
-
output gate:$ o_t = \sigma(W^{(o)}x_t + U^{(o)}h_{t-1} + b^{(o)} ) $
-
メモリーセル:$ \tilde c_t = tanh(W^{(\tilde c)}x_t+U^{(\tilde c)}h_{t-1}+b^{(\tilde c)}, \quad c_t = i_t \circ \tilde c_t+ f_t \circ c_{t-1} $
-
状態の更新:$ h_t = o_t \circ tanh(c_t) $
-
CEC(Constant Error Carousel)
勾配消失および勾配爆発の解決方法として、勾配が1であれば解決できる。
課題:入力データについて、時間依存度に関係なく重みが一律である。
→ ニューラルネットワークの学習特性がないということ。 -
入力ゲートと出力ゲート
入力ゲートと出力ゲートを追加し、それぞれのゲートへの入力値の重みを重み行列W、Uで可変可能とすることにより、CECの課題を解決。 -
忘却ゲート
CECは過去の情報がすべて保管されているが、過去の情報が不要になった場合、削除することはできず保管され続ける。
そこで、過去の情報が不要になった場合、そのタイミングで情報を忘却する昨日として、忘却ゲートが誕生した。 -
覗き穴結合
CECの保存されている過去の情報を任意のタイミングで他のノードに伝播させたり、忘却させたい。
CEC自身の値は、ゲート制御に影響を与えていない。
→ CEC自身の値に重み行列を介して伝播可能にした構造として覗き穴結合。
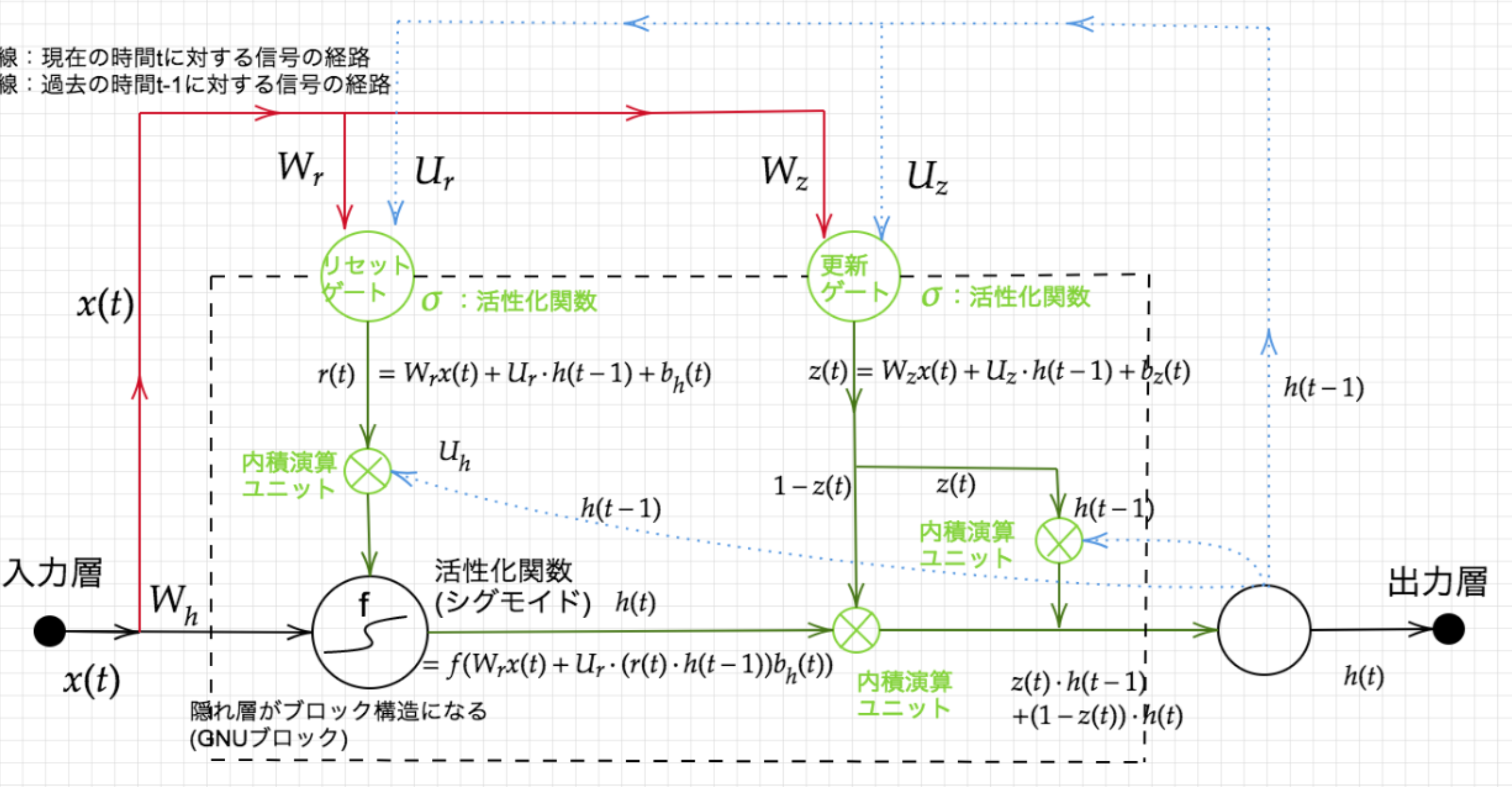
Section3:GRU(Gated Recurrent Unit)
従来のLSTMでは、パラメータが多数存在していたため、計算付加が大きかった。
そこで、GRUではそのパラメータを大幅に削減し、精度は同等またはそれ以上が望めるようになった構造をしている。
- Update gate:$ z_t = \sigma(W^{(z)}x_t + U^{(z)}h_{t-1}) $
- Reset gate:$ r_t = \sigma(W^{(r)}x_t + U^{(r)}h_{t-1}) $
- 状態の更新:$ \tilde h_t = tanh(Wx_t+r_t \circ Uh_{t-1}), \quad h_t = z_t \circ h_{t-1}) + (1-z_t) \circ \tilde h_t $
Reset gateの値が0の場合、前の状態を無視。
Update gateの値が1の場合、前の状態をそのままコピー。
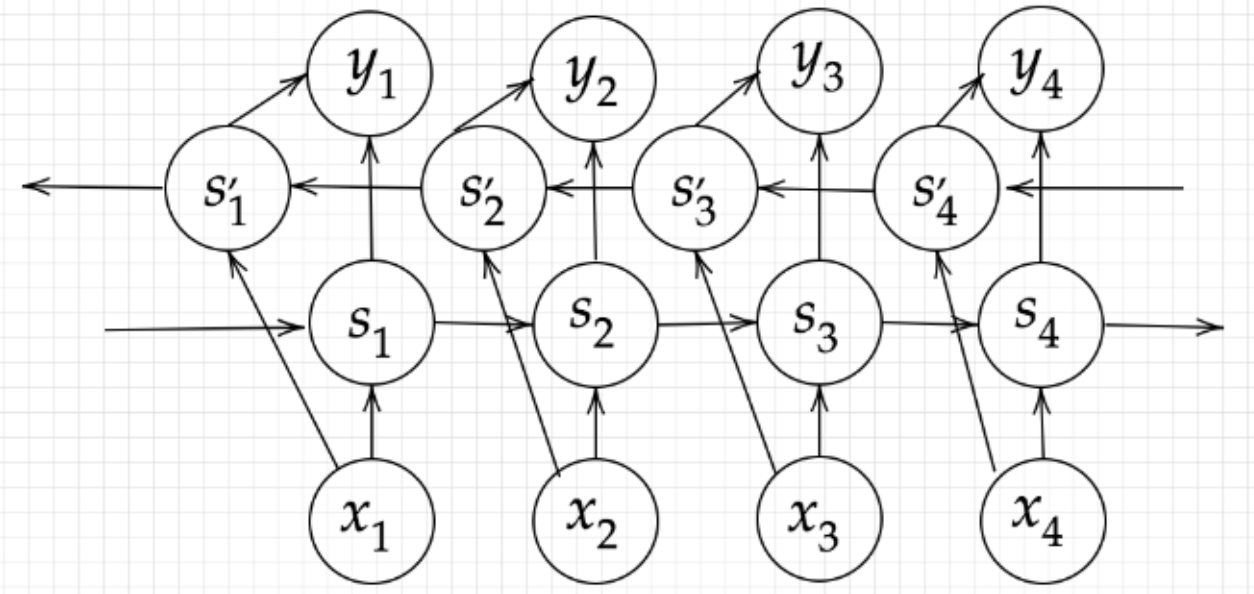
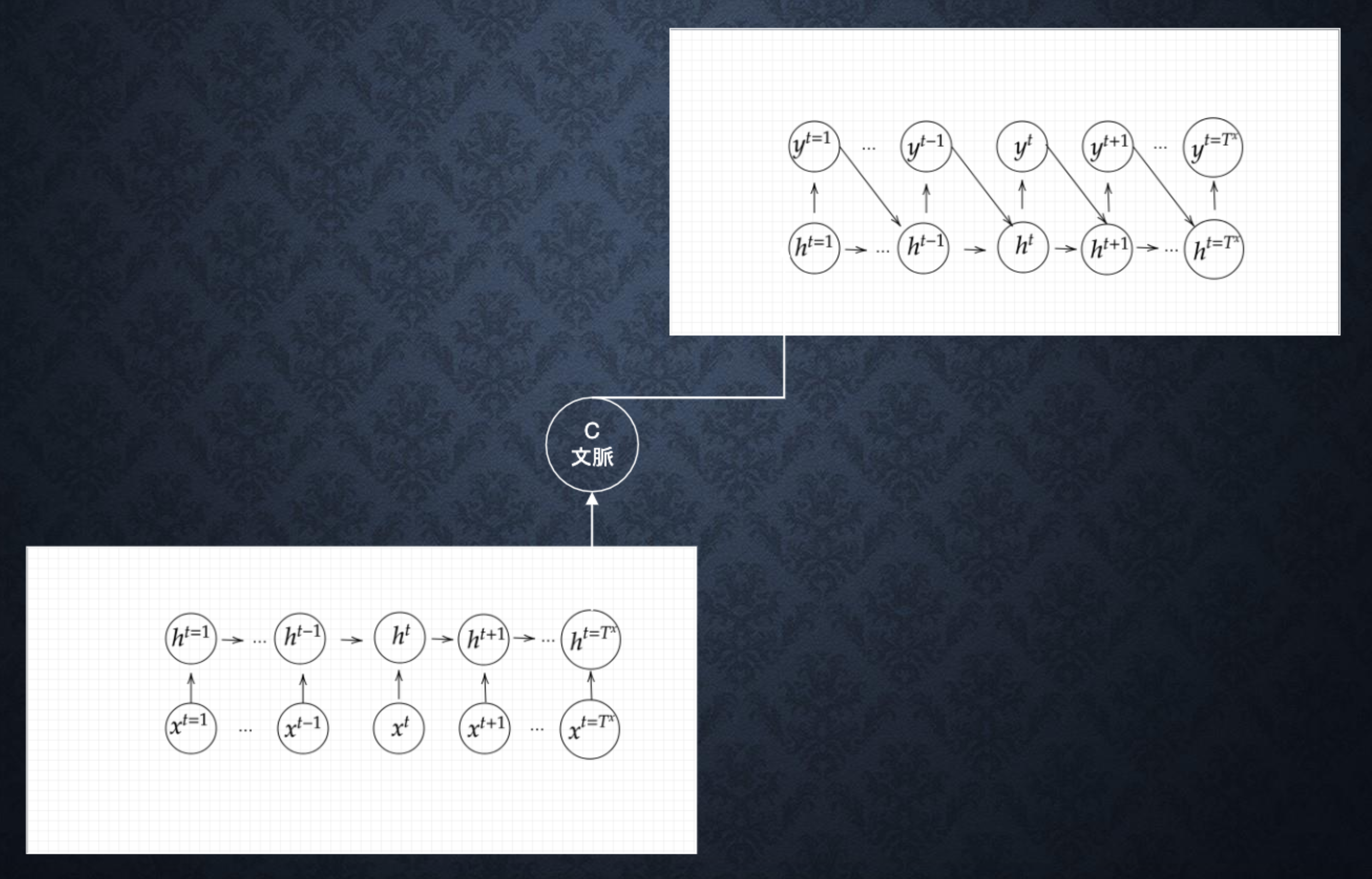
Section4:双方向RNN(Bidirectional RNN)
過去の情報だけでなく、未来の情報を加味することで、精度を向上させるためのモデル。
文章の推敲や機械翻訳に使用される。
Section5:Seq2Seq
通常のRNNは入力と出力の長さや順序が同じでなければならない。
一方、Seq2SeqはEncoder-Decoderモデルの一種で、入力側と出力側で別々のRNNを使う。
機械対話や機械翻訳に使用される。
-
Encoder RNN
ユーザーがインプットしたテキストデータを単語等のトークンに区切って渡す構造。
vec1をRNNに入力し、hidden stateを出力。
このhidden stateと次の入力vec2をまたRNNに入力してきたhidden state
最後のvecを入れたときのhidden stateをfinal stateをしてとっておく。
このfinal stateがthought vectorと呼ばれ、入力した文の意味を表すベクトルとなる。 -
Decoder RNN
システムがアウトプットデータを単語等のトークンごとに生成する構造。
【Decoder RNNの処理手順】
- Decoder RNN:Encoder RNNのfinal state(thought vector)から、各tokenの生成確率を出力していく。final stateをDecoder RNNのinitial stateとして設定し、Embeddingを入力。
- Sampling:生成確率に基いてtokenをランダムに選ぶ。
- Embedding:2で選ばれたtokenをEmbeddingしてDecoder RNNへの次の入力とする。
- Detokenize:1-3を繰り返し、2で得られたtokenを文字列に直す。
-
HRED
過去n-1個の発話から次の発話を生成する。
Seq2seqでは会話の文脈無視で応答がなされたが、HREDでは前の単語の流れに即して応答されるため、より人間らしい文章が生成される。
Seq2seqとContext RNN(Encoderのまとめた各文章の系列をまとめて、これまでの会話コンテキスト全体を表すベクトルに変換する構造)を組み合わせた構造により、過去の発話の履歴を加味した応答を生成している。
課題1:確率的な多様性が字面にしかなく、会話の「流れ」のような多様性がない。
→ 同じコンテキスト(発話リスト)を与えられても、答えの内容が会話の流れとしては毎回同じものしか出せない。
課題2:短く情報量に乏しい答えをしがちである。
→ 短いよくある答えを学ぶ傾向がある。 -
VHRED
HREDにVAEの潜在変数の概念を追加することにより、HREDの課題を解決した構造。 -
VAE
潜在変数zに確率分布を仮定したもの。
Section6:Word2vec
RNNでは、単語のような可変長の文字列をNNに与えることはできない。
word2vecでは学習データからボキャブラリを作成し、「ボキャブラリ数×任意の単語ベクトルの次元数」の重み行列により、大規模データの分散表現の学習を現実的な計算速度とメモリ量で実現可能にした。
結果の数値ベクトルは、生のテキストをデータの視覚化、機械学習、および深層学習に適した数値表現に変換するために使用できる。
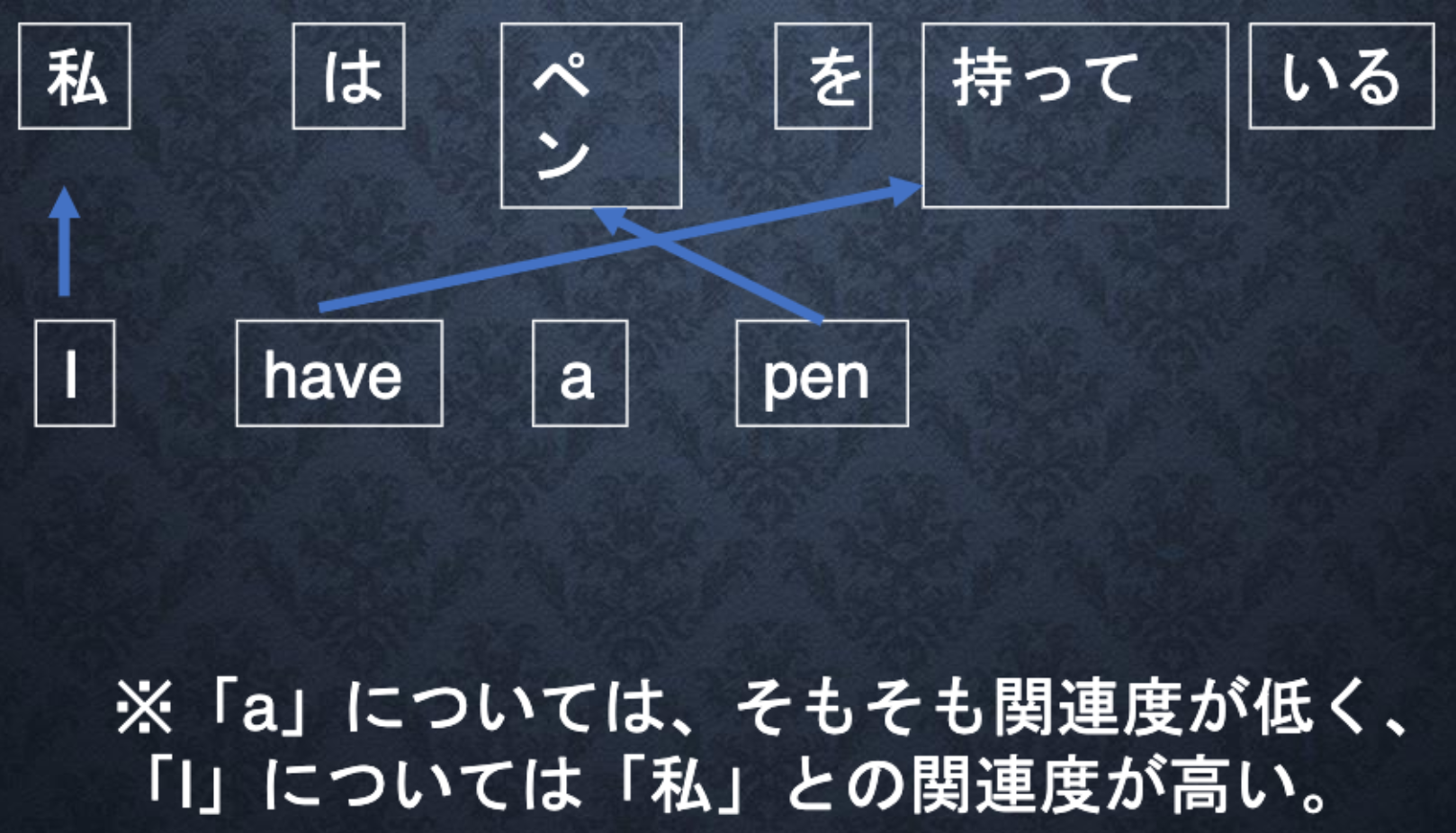
Section7:Attention Mechanism
「入力と出力のどの単語が関連しているか」の関連度を学習する仕組み。
Decoderが各単語を出力する際の情報として、Encoderにおける各単語の隠れ状態の重み付き平均を入力として用いるという方法で、翻訳元の文の文脈情報をより詳細に捉えることができるようになる。
Attentionの機構が導入されたことによって、ニューラル機械翻訳の精度は大きく向上し、従来の統計的機械翻訳モデルの性能を凌駕することとなった。