はじめに
2021/2/19・20に実施される日本ディープラーニング協会(JDLA)E資格合格を目指して、ラビットチャレンジを受講した際の学習記録です。
科目一覧
応用数学
機械学習
深層学習(day1)
深層学習(day2)
深層学習(day3)
深層学習(day4)
全体像
ディープラーニングは、結局何をやろうとしているのか。
→ 重みとバイアスを最適化して、誤差を最小化するパラメータを発見すること。
- 入力層:2ノード1層、中間層:3ノード2層、出力層:1ノード1層のネットワーク

【事前に用意する情報】
入力: $x_n=[x_{n1}…x_{ni}]$
訓練データ: $d_n=[d_{n1}…d_{nk}]$
【多層ネットワークのパラメータ】
$$ w^{(l)} = \left\{ \begin{array} \
重み: & W^{(l)}= \left(
\begin{array}{ccccc}
w_{11}^{(l)} & \cdots & w_{1j}^{(l)} \
\vdots & \ddots & \vdots \
w_{j1}^{(l)} & \cdots & w_{jj}^{(l)} \
\end{array}
\right)\
バイアス: & b^{(l)}=[b_1^{(l)}…b_j^{(l)}] \
\end{array} \right. $$
活性化関数: $f^{(l)}(u^{(l)})=[f^{(l)}(u_1^{(l)})…f^{(l)}(u_j^{(l)})]$
中間層出力: $z^{(l)}=[z_1^{(t)}…z_K^{(t)}]=f^{(l)}(u^{(l)})$
総入力: $u^{(f)}=W^{(l)}z^{(l-1)}+b^{(l)}$
出力: $y_n^{(t)}=[y_{n1}^{(t)}…y_{nK}^{(t)}]=z^{(L)}$
誤差関数: $E_n(w)$
→ $\nabla E_n(w)=\frac{\partial E}{\partial w}$
→ $w^{(t+1)}=w^{(t)}-\epsilon\nabla E_n(w)$
入力層ノードのインデックス: $i , (=1…L)$
中間層ノードのインデックス: $j , (=1…J)$
出力層ノードのインデックス: $k , (=1…K)$
層のインデックス: $l , (=1…L)$
訓練データのインデックス: $n , (=1…N)$
試行回数のインデックス: $t , (=1…T)$
Section1:入力層〜中間層
入力層
$$ z_i^{(1)} = x_i, ; z^{(1)} = x $$
入力ユニットは活性化関数を持たず、単に値 $x_i$ を出すだけ。
入力層はニューラルネットの層数には数えない。
中間層
第 $l$ 層中の $j$ 番目のユニットを考えると、第 $l-1$ 層の各ユニットからの入力 $z_i^{(l-1)}$ を入力として受け入れるので、活性は
$$ u_j^{(l)} = \sum_i w_{ji}^{(l)} z_{i}^{(l-1)} $$
となる。
第 $l-1$ 層のユニット $i$と第 $l$ 層のユニット $j$ の間の結合の重み $w_{ji}^{(l)}$ を $(j,i)$ 成分とする重み行列
$$ W^{(l)} = \left(
\begin{array}{ccccc}
w_{11}^{(l)} & w_{12}^{(l)} & \cdots \
w_{21}^{(l)} & w_{22}^{(l)} & \
\vdots & & \ddots \
\end{array}
\right) $$
を導入し、さらにバイアスもまとめて縦ベクトル $b^{(l)}$
$$ u^{(l)} = W^{(l)}z^{(l-1)}, ; z^{(l)}=f^{(l)}\bigl(u^{(l)}+b^{(l)}\bigl) $$
import numpy as np
def print_vec(text, vec):
print("*** " + text + " ***")
print(vec)
print("shape: " + str(vec.shape))
print("")
# ReLU関数
def relu(x):
return np.maximum(0, x)
# ウェイトとバイアスを設定
# ネートワークを作成
def init_network():
print("##### ネットワークの初期化 #####")
network = {}
network['W1'] = np.random.rand(2,3)
network['W2'] = np.random.rand(3,3)
network['W3'] = np.random.rand(3,1)
network['b1'] = np.random.randn(3)
network['b2'] = np.random.randn(3)
network['b3'] = np.random.randn(1)
print_vec("重み1", np.round(network['W1'], 2))
print_vec("重み2", np.round(network['W2'], 2) )
print_vec("重み3", np.round(network['W3'], 2))
print_vec("バイアス1", np.round(network['b1'], 2))
print_vec("バイアス2", np.round(network['b2'], 2))
print_vec("バイアス3", np.round(network['b3'], 2))
return network
# プロセスを作成
def forward(network, x):
print("##### 順伝播開始 #####")
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
# 1層の総入力
u1 = np.dot(x, W1) + b1
# 1層の総出力
z1 = functions.relu(u1)
# 2層の総入力
u2 = np.dot(z1, W2) + b2
# 2層の総出力
z2 = functions.relu(u2)
# 出力層の総入力
u3 = np.dot(z2, W3) + b3
# 出力層の総出力
y = u3
print_vec("中間層1の総入力", np.round(u1,2))
print_vec("中間層1の総出力", np.round(z1,2))
print_vec("中間層2の総入力", np.round(u2,2))
print_vec("中間層2の総出力", np.round(z2,2))
print_vec("出力層の総入力", np.round(u3,2))
print("出力層の総出力: " + str(np.round(y,2)))
return y, z1, z2
# 入力値
x = np.random.randint(0,2,2)
print_vec("入力", x)
# ネットワークの初期化
network = init_network()
y, z1, z2 = forward(network, x)
Section2:活性化関数
-
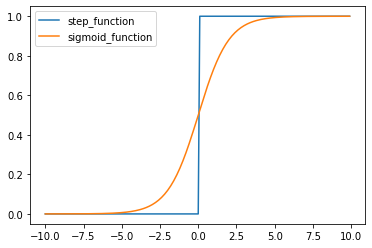
ステップ関数
$$ f(x) = \left\{ \begin{array} \
1 & (x \geq 0) \
0 & (x \lt 0) \
\end{array} \right. $$
閾値を超えたら発火する関数であり、出力は常に1か0である。
課題:0〜1の間の値を表現できず、線形分離可能なものしか学習できない。 -
シグモイド関数
$$ f(u) = \frac{1}{1+e^{-u}} $$
0〜1の間を緩やかに変化する関数で、ステップ関数ではON/OFFしかない状態に対し、信号の強弱を伝えられるようになり、ニューラルネットワーク普及のきっかけとなった。
課題:大きな値では出力の変化が微小なため、勾配消失問題を引き起こすことがある。0になることはないので、計算リソースが常に食われてしまう。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.1)
# step_function
def step(x):
return np.where( x > 0, 1, 0)
y_step = step(x)
plt.plot(x, y_step,label='step_function')
# sigmoid_function
def sigmoid(x):
return 1/(1+np.exp(-x))
y_sigmoid = sigmoid(x)
plt.plot(x, y_sigmoid,label='sigmoid_function')
plt.legend()
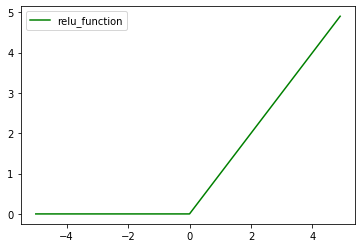
- ReLU関数
$$ f(x) = \left\{ \begin{array} \
x & (x > 0) \
0 & (x \leq 0) \
\end{array} \right. $$
勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている。
# relu_function
def relu(x):
return np.maximum(0,x)
x = np.arange(-5, 5, 0.1)
y_relu = relu(x)
plt.plot(x, y_relu,c='g',label='relu_function')
plt.legend()
Section3:出力層
誤差関数
$$ E_n(w) = \frac{1}{2} \sum_{j=1}^J(y_j-d_j)^2 = \frac{1}{2} ||(y-d)||^2 $$
なぜ引き算ではなく、二乗するか → 値を正にするため
$\frac{1}{2}$ はどういう意味を持つか → 微分を可能にするため
出力層の活性化関数
| 回帰 | 二値分類 | 多クラス分類 | |
|---|---|---|---|
| 活性化関数 | 恒等写像 | シグモイド関数 | ソフトマックス関数 |
| 活性化関数(式) | $f(u)=u$ | $f(u)=\frac{1}{1+e^{-u}}$ | $f(i,u)=\frac{e^{u_i}}{\sum_{k=1}^K e^{u_k}}$ |
| 誤差関数 | 二乗誤差 | 交差エントロピー | 交差エントロピー |
Section4:勾配降下法
深層学習の目的は、学習を通して誤差を最小にするネットワークを作成すること
→ 誤差 $E(w)$ を最小化するパラメータ $w$ を発見すること
$$ \text{誤差勾配} \quad \nabla E = \frac{\partial E}{\partial w} = \Bigl[\frac{\partial E}{\partial w_1}…\frac{\partial E}{\partial w_M}\Bigl] $$
| 勾配降下法 | 確率的勾配降下法(SGD) | ミニバッチ勾配降下法 | |
|---|---|---|---|
| 式 | $w^{(t+1)}=w^{(t)}-\epsilon\nabla{E}$ | $w^{(t+1)}=w^{(t)}-\epsilon\nabla{E_n}$ | $w^{(t+1)}=w^{(t)}-\epsilon\nabla{E_t}, ; E_t=\frac{1}{N_t}\sum_{n \in D_t}{E_n}, ; N_t= D_t $ |
| 特徴 | 全サンプルの平均誤差 | ランダムに抽出したサンプルの誤差 | ランダムに分割したデータの集合(ミニバッチ)$D_t$に属するサンプルの平均誤差 |
| メリット | データが冗長な場合の計算コストの軽減。望まない局所極小解に収束するリスクの軽減。オンライン学習ができる。 | 確率的勾配法のメリットを損なわず、計算機の計算資源を有効利用できる。 |
import numpy as np
import matplotlib.pyplot as plt
# ReLU関数
def relu(x):
return np.maximum(0, x)
# 平均二乗誤差
def mean_squared_error(d, y):
return np.mean(np.square(d - y)) / 2
# ReLU関数の導関数
def d_relu(x):
return np.where( x > 0, 1, 0)
# 平均二乗誤差の導関数
def d_mean_squared_error(d, y):
if type(d) == np.ndarray:
batch_size = d.shape[0]
dx = (y - d)/batch_size
else:
dx = y - d
return dx
# サンプルとする関数
def f(x):
y = 3 * x[0] + 2 * x[1]
return y
# 初期設定
def init_network():
network = {}
nodesNum = 5
network['W1'] = np.random.randn(2, nodesNum)
network['W2'] = np.random.randn(nodesNum)
network['b1'] = np.random.randn(nodesNum)
network['b2'] = np.random.randn()
return network
# 順伝播
def forward(network, x):
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
u1 = np.dot(x, W1) + b1
z1 = relu(u1)
u2 = np.dot(z1, W2) + b2
y = u2
return z1, y
# 誤差逆伝播
def backward(x, d, z1, y):
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
# 出力層でのデルタ
delta2 = d_mean_squared_error(d, y)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
delta1 = np.dot(delta2, W2.T) * d_relu(z1)
delta1 = delta1[np.newaxis, :]
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
x = x[np.newaxis, :]
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
return grad
# サンプルデータを作成
data_sets_size = 100000
data_sets = [0 for i in range(data_sets_size)]
for i in range(data_sets_size):
data_sets[i] = {}
# ランダムな値を設定
data_sets[i]['x'] = np.random.rand(2)
# 目標出力を設定
data_sets[i]['d'] = f(data_sets[i]['x'])
losses = []
# 学習率
learning_rate = 0.05
# 抽出数
epoch = 1000
# パラメータの初期化
network = init_network()
# データのランダム抽出
random_datasets = np.random.choice(data_sets, epoch)
# 勾配降下の繰り返し
for dataset in random_datasets:
x, d = dataset['x'], dataset['d']
z1, y = forward(network, x)
grad = backward(x, d, z1, y)
# パラメータに勾配適用
for key in ('W1', 'W2', 'b1', 'b2'):
network[key] -= learning_rate * grad[key]
# 誤差
loss = mean_squared_error(d, y)
losses.append(loss)
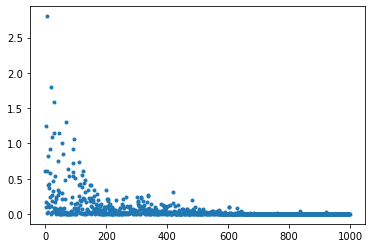
print("##### 結果表示 #####")
lists = range(epoch)
plt.plot(lists, losses, '.')
# グラフの表示
plt.show()
Section5:誤差逆伝播法
誤差勾配を数値微分 $ \frac{\partial E}{\partial w_m} = \frac{E(w_m+h)-E(w_m-h)}{2h}$で計算すると、各パラメータ $w_m$ それぞれについて $E(w_m+h)$ や $E(w_m-h)$ を計算するために、順伝播の計算を繰り返し行う必要があり負荷が大きい。
そこで、誤差逆伝播法を利用する。
誤差逆伝播法とは、算出された誤差を出力層側から順に微分し、前の層へと伝播することにより、不要な再帰的計算を避けて各パラメータの微分値を計算する手法。