Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@yoshiko__

【ラビットチャレンジ（E資格）】深層学習（day4）

Last updated at Posted at 2020-08-02

#はじめに
2021/2/19・20に実施される日本ディープラーニング協会(JDLA)Ｅ資格合格を目指して、ラビットチャレンジを受講した際の学習記録です。

###科目一覧
応用数学
機械学習
深層学習（day1）
深層学習（day2）
深層学習（day3）
深層学習（day4）

#Section1：実装演習
##Tensorflow

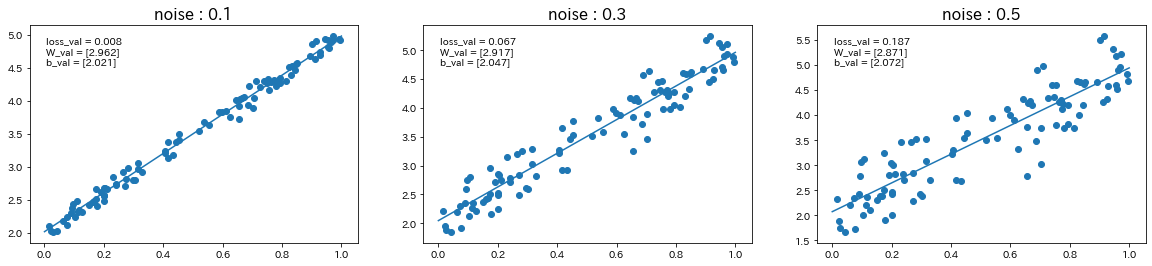
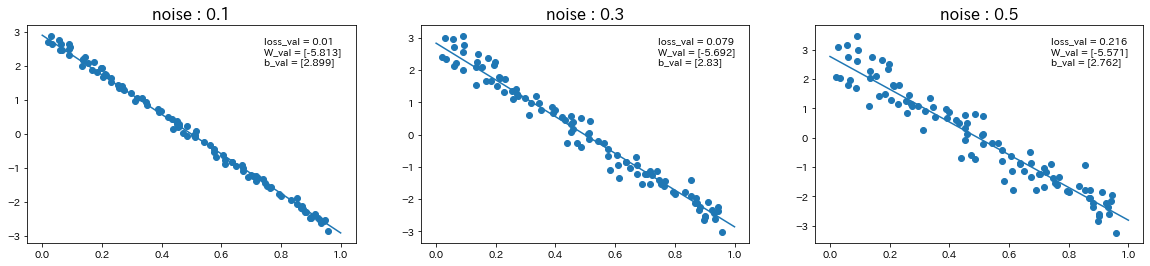
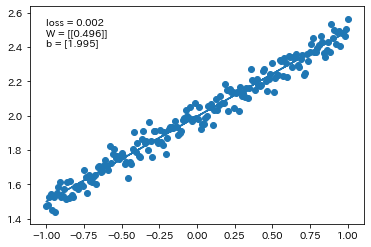
####線形回帰

  • $d=3x+2$の関数に対して、ノイズの値を変更
    image.png

  • 関数$d$を$d=-6x+3$に変更して、ノイズの値も変更
    image.png

→ ノイズの値が大きいほど、誤差が大きくなり、予測精度が下がることが確認された。

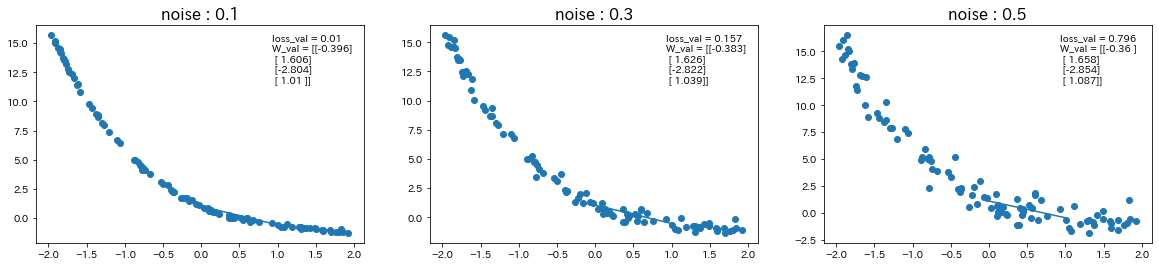
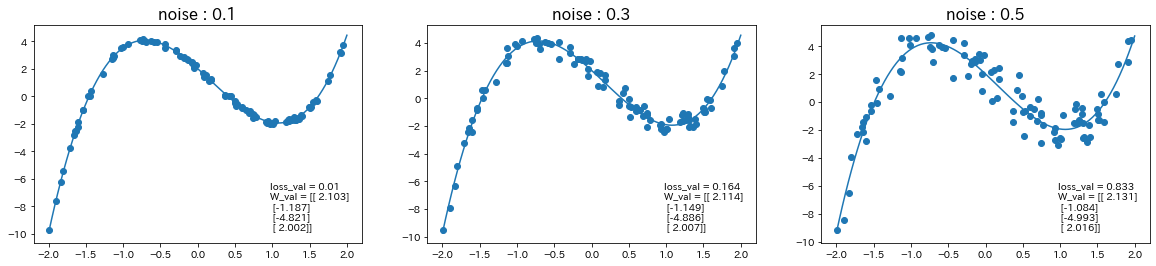
####非線形回帰

  • $d=-0.4x^3+1.6x^2-2.8x+1$の関数に対して、ノイズの値を変更
    image.png

  • 関数$d$を$d=2.1x^3-1.2x^2-4.8x+2$に変更して、ノイズの値も変更
    image.png

→ ノイズの値が大きいほど、誤差が大きくなり、予測精度が下がることが確認された。

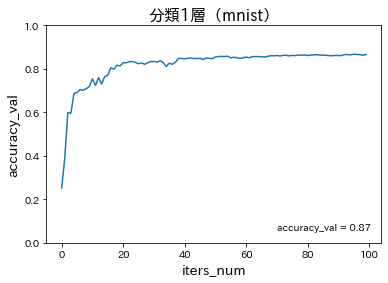
####分類1層（mnist）
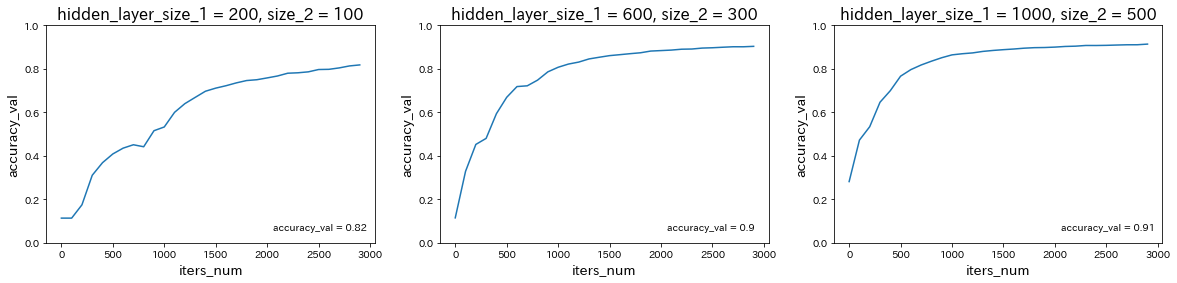
image.png

####分類3層（mnist）

  • 隠れ層のサイズを変更
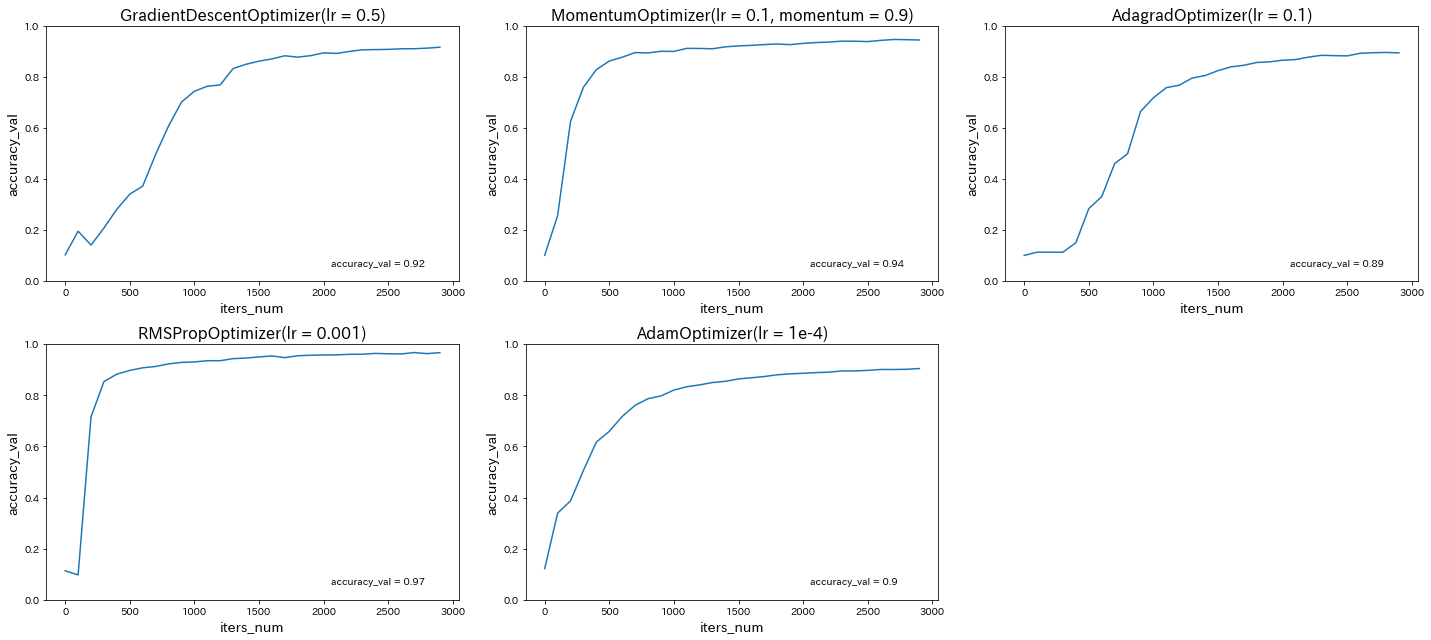
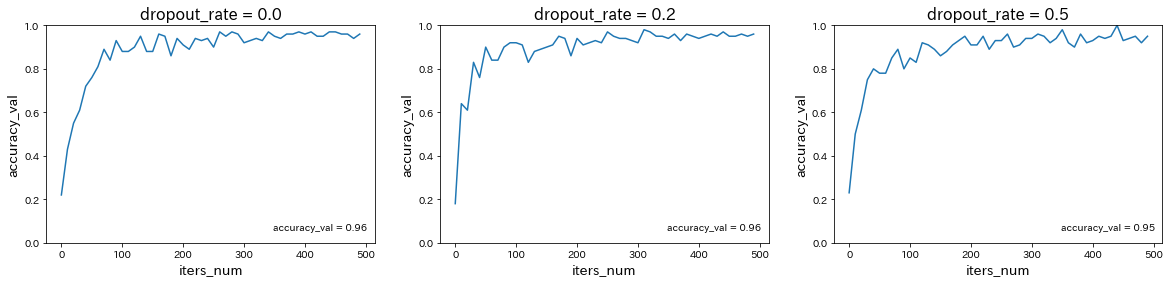
    image.png
    → 隠れ層のサイズが大きいほど、予測精度が上がることが確認された。

  • optimizerを変更
    image.png

####分類CNN（mnist）
image.png

##keras
####線形回帰
image.png

####単純パーセプトロン

Simple_perceptron
# モジュール読み込み
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
 
# 乱数を固定値で初期化
np.random.seed(0)

# シグモイドの単純パーセプトロン作成
model = Sequential()
model.add(Dense(input_dim=2, units=1))
model.add(Activation('sigmoid'))
model.summary()

model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
 
# トレーニング用入力 X と正解データ T
X = np.array( [[0,0], [0,1], [1,0], [1,1]] )
T = np.array( [[0], [1], [1], [1]] )
 
# トレーニング
model.fit(X, T, epochs=30, batch_size=1)
 
# トレーニングの入力を流用して実際に分類
Y = model.predict_classes(X, batch_size=1)

print("TEST")
print(Y == T)
  • np.random.seed(0)をnp.random.seed(1)に変更

発生する乱数が下記のような異なる値で固定されることになるので、学習結果も変わる。

np.random.seed()
import numpy as np
 
# 乱数を固定値で初期化
np.random.seed(0)
print(np.random.randn()) -> 1.764052345967664
# 乱数を固定値で初期化
np.random.seed(1)
print(np.random.randn()) -> 1.6243453636632417
  • エポック数を100に変更

エポック数を増加させると、lossは減少することが確認された。

  • AND回路, XOR回路に変更

OR回路、AND回路は線形分離可能だが、XORは線形分離不可能なので学習できないことが確認された。

  • OR回路にしてバッチサイズを10に変更

バッチサイズを増加させると、lossは増加することが確認された。

  • エポック数を300に変更

エポック数を増加させると、lossは減少することが確認された。

####分類（iris）

classifiy_iris
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
x = iris.data
d = iris.target

from sklearn.model_selection import train_test_split
x_train, x_test, d_train, d_test = train_test_split(x, d, test_size=0.2)

from keras.models import Sequential
from keras.layers import Dense, Activation
# from keras.optimizers import SGD

#モデルの設定
model = Sequential()
model.add(Dense(12, input_dim=4))
model.add(Activation('relu'))
# model.add(Activation('sigmoid'))
model.add(Dense(3, input_dim=12))
model.add(Activation('softmax'))
model.summary()

model.compile(optimizer='sgd', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

history = model.fit(x_train, d_train, batch_size=5, epochs=20, verbose=1, validation_data=(x_test, d_test))
loss = model.evaluate(x_test, d_test, verbose=0)

#Accuracy
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.ylabel('accuracy', fontsize=14)
plt.xlabel('epoch', fontsize=14)
plt.legend(['train', 'test'], loc='lower right', fontsize=14)
plt.ylim(0, 1.0)
plt.show()

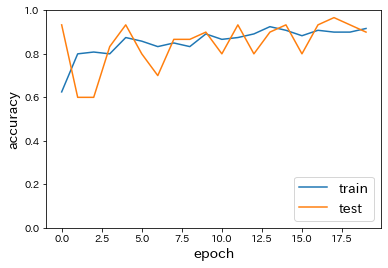
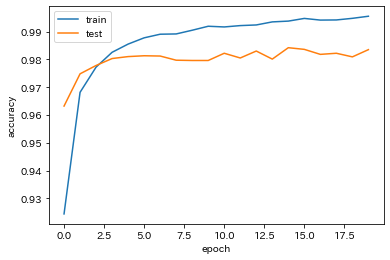
image.png

  • 中間層の活性関数をsigmoidに変更

→　accuracyの減少が確認された。

image.png

  • SGDをimportし、optimizerをSGD(lr=0.1)に変更

→　epochごとのaccuracyのばらつきが増加したように思われる。

image.png

####分類（mnist）

classify_mnist
# 必要なライブラリのインポート
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import keras
import matplotlib.pyplot as plt
from data.mnist import load_mnist

(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)

# 必要なライブラリのインポート、最適化手法はAdamを使う
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.optimizers import Adam

# モデル作成
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dropout(0.2))
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(10, activation='softmax'))
model.summary()

# バッチサイズ、エポック数
batch_size = 128
epochs = 20

model.compile(loss='categorical_crossentropy', 
              optimizer=Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False), 
              metrics=['accuracy'])

history = model.fit(x_train, d_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_test, d_test))
loss = model.evaluate(x_test, d_test, verbose=0)
print('Test loss:', loss[0])
print('Test accuracy:', loss[1])

# Accuracy
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
# plt.ylim(0, 1.0)
plt.show()

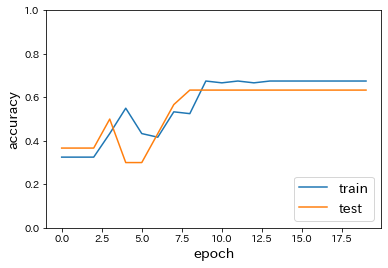
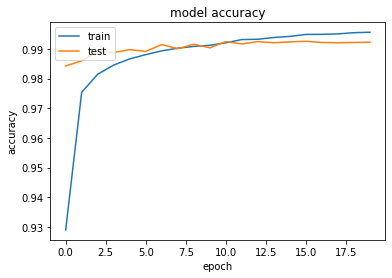
image.png

  • load_mnistのone_hot_labelをFalseに変更、または誤差関数をsparse_categorical_crossentropyに変更
    →　誤差関数として'categorical_crossentropy'を使う場合はデータの形式をone_hot_label形式に、'sparse_categorical_crossentropy'を使う場合はone_hot_labelではない形式にする必要がある。

  • Adamの引数の値を変更
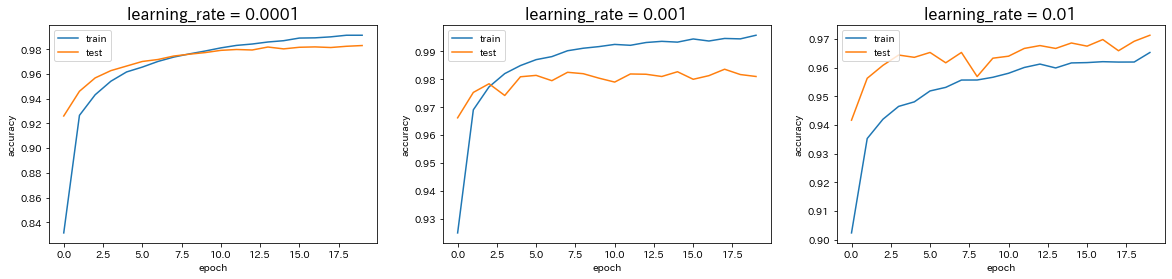
    image.png
    →　学習率を0.0001から0.001に変更すると、予測精度はほぼ変わらないが、学習の早さは向上した。しかし、学習率を0.001からさらに0.01に変更すると、予測精度が低下した。

####CNN分類（mnist）

classify_mnist_with_CNN
# 必要なライブラリのインポート
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import keras
import matplotlib.pyplot as plt
from data.mnist import load_mnist

(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)


# 行列として入力するための加工
batch_size = 128
num_classes = 10
epochs = 20

img_rows, img_cols = 28, 28

x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)


# 必要なライブラリのインポート、最適化手法はAdamを使う
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.optimizers import Adam

model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
                 activation='relu',
                 input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.summary()

# バッチサイズ、エポック数
batch_size = 128
epochs = 20

model.compile(loss='categorical_crossentropy', optimizer=Adam(), metrics=['accuracy'])
history = model.fit(x_train, d_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_test, d_test))

# Accuracy
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
# plt.ylim(0, 1.0)
plt.show()

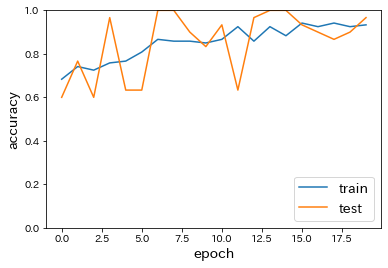
image.png

→　CNNにより、99%以上という非常に高い予測精度が得られることが確認された。

####CIFAR-10

classify_cifar10
#CIFAR-10のデータセットのインポート
from keras.datasets import cifar10
(x_train, d_train), (x_test, d_test) = cifar10.load_data()

#CIFAR-10の正規化
from keras.utils import to_categorical
  
# 特徴量の正規化
x_train = x_train/255.
x_test = x_test/255.
 
# クラスラベルの1-hotベクトル化
d_train = to_categorical(d_train, 10)
d_test = to_categorical(d_test, 10)
 
# CNNの構築
import keras
from keras.models import Sequential
from keras.layers.convolutional import Conv2D, MaxPooling2D
from keras.layers.core import Dense, Dropout, Activation, Flatten
import numpy as np
 
model = Sequential()
 
model.add(Conv2D(32, (3, 3), padding='same',input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
 
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
 
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(10))
model.add(Activation('softmax'))
 
# コンパイル
model.compile(loss='categorical_crossentropy',optimizer='adam',metrics=['accuracy'])
 
#訓練
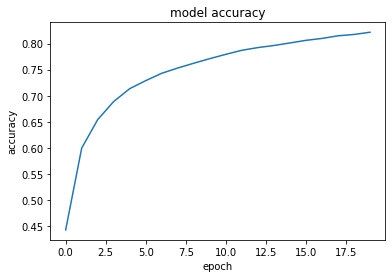
history = model.fit(x_train, d_train, epochs=20)
tf.executing_eagerly()

#評価 & 評価結果出力
print(model.evaluate(x_test, d_test))

# Accuracy
plt.plot(history.history['accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.show()

# モデルの保存
# model.save('./CIFAR-10.h5')

image.png

####RNN（2進数足し算の予測）

RNN（2進数足し算の予測）
# import tensorflow as tf
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()

# logging levelを変更
tf.logging.set_verbosity(tf.logging.ERROR)

import numpy as np
import matplotlib.pyplot as plt

import keras
from keras.models import Sequential
from keras.layers.core import Dense, Dropout,Activation
from keras.layers.wrappers import TimeDistributed
from keras.optimizers import SGD
from keras.layers.recurrent import SimpleRNN, LSTM, GRU


# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)

# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)], dtype=np.uint8).T,axis=1)[:, ::-1]


# A, B初期化 (a + b = d)
a_int = np.random.randint(largest_number/2, size=20000)
a_bin = binary[a_int] # binary encoding
b_int = np.random.randint(largest_number/2, size=20000)
b_bin = binary[b_int] # binary encoding

x_int = []
x_bin = []
for i in range(10000):
    x_int.append(np.array([a_int[i], b_int[i]]).T)
    x_bin.append(np.array([a_bin[i], b_bin[i]]).T)

x_int_test = []
x_bin_test = []
for i in range(10001, 20000):
    x_int_test.append(np.array([a_int[i], b_int[i]]).T)
    x_bin_test.append(np.array([a_bin[i], b_bin[i]]).T)

x_int = np.array(x_int)
x_bin = np.array(x_bin)
x_int_test = np.array(x_int_test)
x_bin_test = np.array(x_bin_test)


# 正解データ
d_int = a_int + b_int
d_bin = binary[d_int][0:10000]
d_bin_test = binary[d_int][10001:20000]

model = Sequential()

model.add(SimpleRNN(units=16,
               return_sequences=True,
               input_shape=[8, 2],
               go_backwards=False,
               activation='relu',
               # dropout=0.5,
               # recurrent_dropout=0.3,
               # unroll = True,
            ))
# 出力層
model.add(Dense(1, activation='sigmoid', input_shape=(-1,2)))
model.summary()
model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.1), metrics=['accuracy'])
# model.compile(loss='mse', optimizer='adam', metrics=['accuracy'])

history = model.fit(x_bin, d_bin.reshape(-1, 8, 1), epochs=5, batch_size=2)

# テスト結果出力
score = model.evaluate(x_bin_test, d_bin_test.reshape(-1,8,1), verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])

Epoch 1/5
10000/10000 [==============================] - 28s 3ms/step - loss: 0.0810 - accuracy: 0.9156
Epoch 2/5
10000/10000 [==============================] - 28s 3ms/step - loss: 0.0029 - accuracy: 1.0000
Epoch 3/5
10000/10000 [==============================] - 28s 3ms/step - loss: 9.7898e-04 - accuracy: 1.0000
Epoch 4/5
10000/10000 [==============================] - 28s 3ms/step - loss: 4.8765e-04 - accuracy: 1.0000
Epoch 5/5
10000/10000 [==============================] - 28s 3ms/step - loss: 3.3379e-04 - accuracy: 1.0000
Test loss: 0.0002865186012966387
Test accuracy: 1.0

  • RNNの出力ノード数を128に変更
    Epoch 1/5
    10000/10000 [==============================] - 29s 3ms/step - loss: 0.0741 - accuracy: 0.9194
    Epoch 2/5
    10000/10000 [==============================] - 29s 3ms/step - loss: 0.0020 - accuracy: 1.0000
    Epoch 3/5
    10000/10000 [==============================] - 29s 3ms/step - loss: 6.9808e-04 - accuracy: 1.0000
    Epoch 4/5
    10000/10000 [==============================] - 28s 3ms/step - loss: 4.0773e-04 - accuracy: 1.0000
    Epoch 5/5
    10000/10000 [==============================] - 28s 3ms/step - loss: 2.8269e-04 - accuracy: 1.0000
    Test loss: 0.0002439875359702302
    Test accuracy: 1.0
    →　出力ノード数を16から128に変更した場合、予測精度が向上した。

  • RNNの出力活性化関数をsigmoidに変更
    Epoch 1/5
    10000/10000 [==============================] - 28s 3ms/step - loss: 0.2498 - accuracy: 0.5131
    Epoch 2/5
    10000/10000 [==============================] - 28s 3ms/step - loss: 0.2487 - accuracy: 0.5302
    Epoch 3/5
    10000/10000 [==============================] - 28s 3ms/step - loss: 0.2469 - accuracy: 0.5481
    Epoch 4/5
    10000/10000 [==============================] - 28s 3ms/step - loss: 0.2416 - accuracy: 0.6096
    Epoch 5/5
    10000/10000 [==============================] - 27s 3ms/step - loss: 0.2166 - accuracy: 0.7125
    Test loss: 0.18766544096552618
    Test accuracy: 0.7449744939804077
    →　出力活性化関数をReLUからsigmoidに変更した場合、予測精度が低下した。

  • RNNの出力活性化関数をtanhに変更
    Epoch 1/5
    10000/10000 [==============================] - 28s 3ms/step - loss: 0.1289 - accuracy: 0.8170
    Epoch 2/5
    10000/10000 [==============================] - 28s 3ms/step - loss: 0.0022 - accuracy: 1.0000
    Epoch 3/5
    10000/10000 [==============================] - 28s 3ms/step - loss: 7.1403e-04 - accuracy: 1.0000
    Epoch 4/5
    10000/10000 [==============================] - 27s 3ms/step - loss: 4.1603e-04 - accuracy: 1.0000
    Epoch 5/5
    10000/10000 [==============================] - 28s 3ms/step - loss: 2.8925e-04 - accuracy: 1.0000
    Test loss: 0.00024679134038564263
    Test accuracy: 1.0
    →　出力活性化関数をReLUからTanhに変更すると、予測精度が向上した。

  • 最適化方法をadamに変更
    Epoch 1/5
    10000/10000 [==============================] - 31s 3ms/step - loss: 0.0694 - accuracy: 0.9385
    Epoch 2/5
    10000/10000 [==============================] - 32s 3ms/step - loss: 0.0012 - accuracy: 1.0000
    Epoch 3/5
    10000/10000 [==============================] - 31s 3ms/step - loss: 5.4037e-05 - accuracy: 1.0000
    Epoch 4/5
    10000/10000 [==============================] - 31s 3ms/step - loss: 3.3823e-06 - accuracy: 1.0000
    Epoch 5/5
    10000/10000 [==============================] - 31s 3ms/step - loss: 2.4213e-07 - accuracy: 1.0000
    Test loss: 5.572893907904208e-08
    Test accuracy: 1.0
    →　最適化方法をsgdからadamに変更すると、予測精度が向上した。

  • RNNの入力Dropoutを0.5に設定
    Epoch 1/5
    10000/10000 [==============================] - 30s 3ms/step - loss: 0.2324 - accuracy: 0.5875
    Epoch 2/5
    10000/10000 [==============================] - 31s 3ms/step - loss: 0.2106 - accuracy: 0.6230
    Epoch 3/5
    10000/10000 [==============================] - 31s 3ms/step - loss: 0.2046 - accuracy: 0.6264
    Epoch 4/5
    10000/10000 [==============================] - 31s 3ms/step - loss: 0.2032 - accuracy: 0.6244
    Epoch 5/5
    10000/10000 [==============================] - 30s 3ms/step - loss: 0.1995 - accuracy: 0.6350
    Test loss: 0.15461890560702712
    Test accuracy: 0.8619986772537231
    →　入力Dropoutを0.5に設定すると、学習が進まなくなった。

  • RNNの再帰Dropoutを0.3に設定
    Epoch 1/5
    10000/10000 [==============================] - 32s 3ms/step - loss: 0.1459 - accuracy: 0.8306
    Epoch 2/5
    10000/10000 [==============================] - 32s 3ms/step - loss: 0.0947 - accuracy: 0.9058
    Epoch 3/5
    10000/10000 [==============================] - 32s 3ms/step - loss: 0.0895 - accuracy: 0.9099
    Epoch 4/5
    10000/10000 [==============================] - 31s 3ms/step - loss: 0.0881 - accuracy: 0.9112
    Epoch 5/5
    10000/10000 [==============================] - 31s 3ms/step - loss: 0.0871 - accuracy: 0.9120
    Test loss: 0.09418297858566198
    Test accuracy: 0.9016276597976685
    →　再帰Dropoutを0.3に設定すると、予測精度が低下した。

  • RNNのunrollをTrueに設定
    Epoch 1/5
    10000/10000 [==============================] - 20s 2ms/step - loss: 0.0938 - accuracy: 0.8871
    Epoch 2/5
    10000/10000 [==============================] - 20s 2ms/step - loss: 0.0032 - accuracy: 0.9999
    Epoch 3/5
    10000/10000 [==============================] - 20s 2ms/step - loss: 9.4733e-04 - accuracy: 1.0000
    Epoch 4/5
    10000/10000 [==============================] - 21s 2ms/step - loss: 5.3410e-04 - accuracy: 1.0000
    Epoch 5/5
    10000/10000 [==============================] - 20s 2ms/step - loss: 3.6424e-04 - accuracy: 1.0000
    Test loss: 0.0003125413816745379
    Test accuracy: 1.0
    →　unrollをTrueに設定（ループせずに計算を行う）した場合、予測精度がわずかに低下した。メモリが集約されたため、計算時間は早くなった。

#Section2：強化学習

####強化学習とは
長期的に報酬を最大化できるように環境の中で行動を選択できるエージェントを作ることを目標とする機械学習の一分野。
→　行動の結果として与えられる利益（報酬）を基に、行動を決定する原理を改善していく仕組み。

教師あり学習および教師なし学習では、データから予測すること、データに含まれるパターンを見つけ出すのがそれぞれの目標である。
一方、強化学習では、優れた方策を見つけることが目標。
環境について事前に完璧な知識があれば、最適な行動を予測し決定することは可能であるが、強化学習では不完全な知識を基に行動しながら、データを収集し最適な行動を見つけていく。

  • Q学習
    行動する毎に行動価値関数を更新することにより学習を進める手法。

  • 関数近似法
    価値関数や方策関数を関数近似する手法。

####探索と利用のトレードオフ
過去のデータでベストとされる行動のみを常にとり続ければ、他のさらにベストな行動を見つけることはできない。（探索が足りない状態）
$\longleftrightarrow$　未知の行動のみを常にとり続ければ、過去の経験が活かせない、（利用が足りない状態）

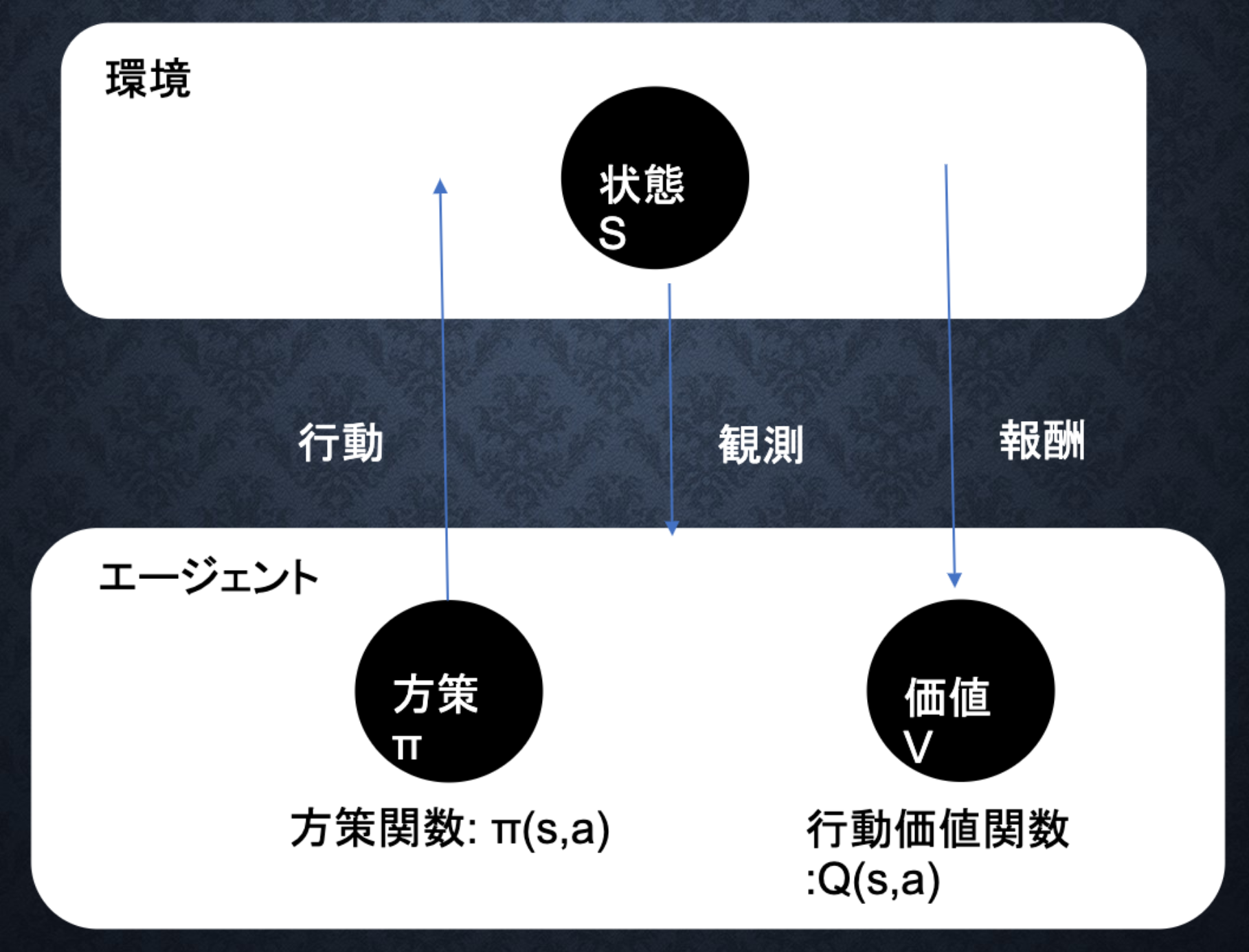
####強化学習のイメージ
image.png

####行動価値関数
価値を表す関数として、状態価値関数（ある状態に注目する場合）と行動価値関数（状態と価値を組み合わせた価値に注目する場合）の2種類がある。

####方策関数
方策関数とは、方策ベースの強化学習手法において、ある状態でどのような行動をとるのかの確率を与える関数のこと。

####方策勾配法
$$ \theta^{(t+1)} = \theta^{(t)}+\epsilon \nabla J(\theta) $$

0
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?