前回に続いて統計学実践手法のお話です。最初の表を思い出してください。多変量解析についても大詰めです。今日は重回帰分析の話です。
回帰分析は以前も登場しましたが、 1 つあるいは複数の変数の値を用いてある 1 つの変数の値を予測する回帰式を導く多変量解析の一種です。
わかりやすい説明としては統計学が最強の学問である実践編 p216 以降を参照してください。
サンプルデータ
統計学が最強の学問である実践編 数学的補足 15 (p61) にあるサンプルデータを利用して重回帰分析をやってみます。引用元では数学的計算方法が掲載されていますので、数式が必要なかたは書籍を参照してください。
| 名前 | 訪問回数 | 男性 | 獲得契約数 |
|---|---|---|---|
| F | 1 | 0 | 2 |
| G | 2 | 0 | 5 |
| H | 3 | 0 | 5 |
| I | 3 | 1 | 0 |
| J | 4 | 1 | 3 |
| K | 5 | 1 | 3 |
上記は営業マンの営業情報とその成績 (獲得契約数) です。
R で分析してみる
df = read.csv("sample_data.csv")
row.names(df) = df[,1]
df = df[,2:4]
head(df)
a <- df[,1]
b <- df[,2]
y <- df[,3]
result = lm(y ~ a + b)
summary(result)
lm(y ~ a + b) の部分が formula オブジェクトと言われるものです。これは回帰系の関数に用いられる独特の記法です。この記事の解説が詳しいです。
数式と同じで左側にある分析対象となる変数を書きます。これを独立変数 (あるいは説明変数など) と言います。右側に群わけのための変数を書きます。これを従属変数 (あるいは目的変数など) と言います。
右側の変数が 1 つなら単回帰分析、複数なら重回帰分析となります。 formula オブジェクトでは複数の変数を + でつないで記述し、数式のイコールに相当するものとして ~ を記述します。
ロジスティック回帰の回でも glm() で同じ formula オブジェクトを記述しました。あわせて参照してください。
出力は以下の通りになります。
Call:
lm(formula = y ~ a + b)
Residuals:
1 2 3 4 5 6
-0.5 1.0 -0.5 -0.5 1.0 -0.5
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.000 1.155 0.866 0.4502
a 1.500 0.500 3.000 0.0577 .
b -5.000 1.291 -3.873 0.0305 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1 on 3 degrees of freedom
Multiple R-squared: 0.8333, Adjusted R-squared: 0.7222
F-statistic: 7.5 on 2 and 3 DF, p-value: 0.06804
この場合 Estimate の部分から以下の回帰式が求められたことになります。
y = 1 + 1.5x_1 - 5x_2
この場合 1 を切片、 1.5 や -5 の部分を偏回帰係数と言います。また上の回帰式にはありませんが、予測の誤差を 残差 (residuals) と言います。
Excel でやってみる
重回帰分析のようないわゆる典型的な統計手法については、実は Microsoft Excel を使うのがきわめて簡単です。
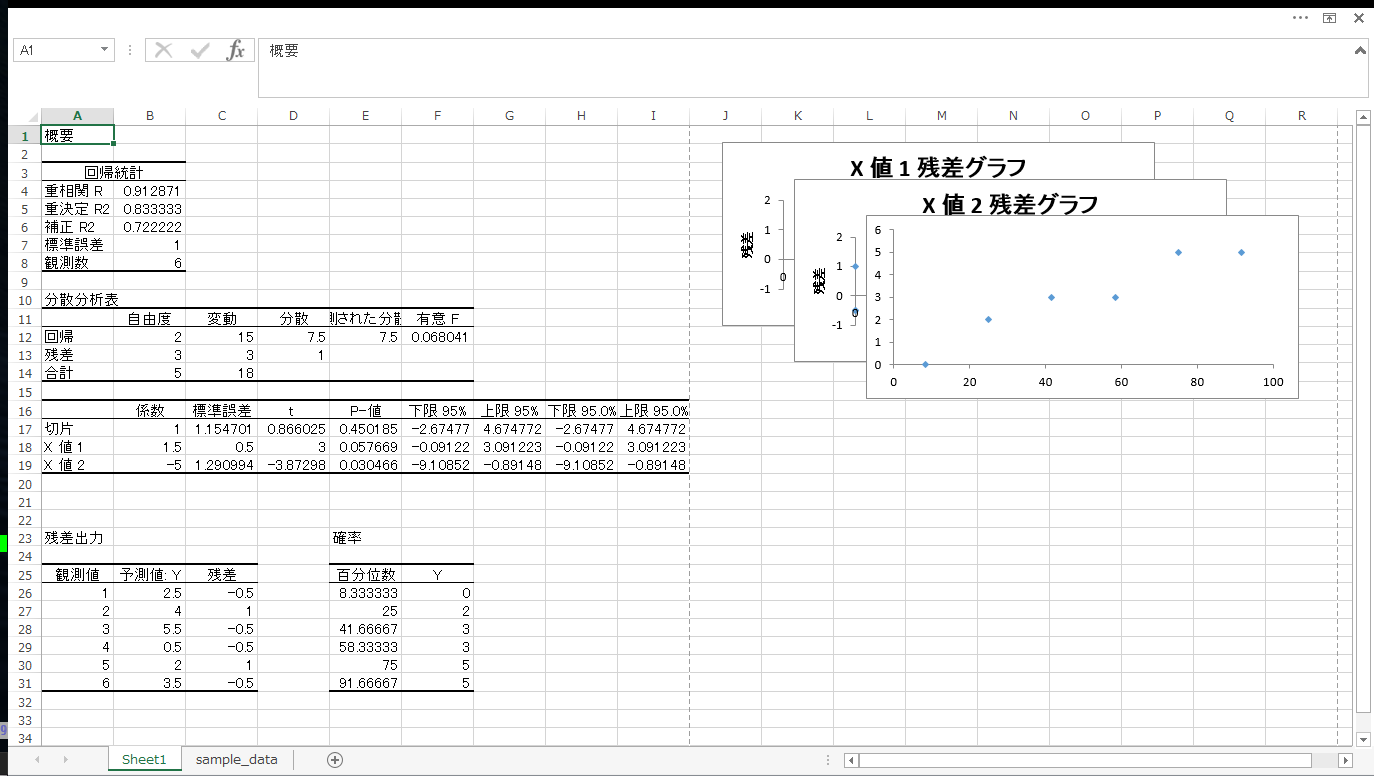
やりかたは [データ] - [データ分析] から「回帰分析」を選びます。入力範囲を複数の従属変数にすることで重回帰分析ができます。
なお左上にある重相関 R は重相関係数のことであり説明変数と従属変数の間の関係の強さを示します。
重決定 R2 は重決定係数または寄与率とも言います。回帰式の母集団へのあてはまりの良さを示します。
補正 R2 は「自由度決定係数」です。自由度の影響を受けて寄与率が実際よりも大きくなってしまう部分を調整した決定係数となります。
Excel の分析ツールと他の方法
分析ツールには以下のようなものが用意されています。
| Excel の項目 | 他の方法、補足説明等 |
|---|---|
| 相関 | pandas の corr() |
| 共分散 | pandas の cov() |
| 基本統計量 | pandas の describe() |
| 指数平滑 | pandas.stats.moments.ewma |
| F 検定 | |
| フーリエ解析 | |
| ヒストグラム | plt.hist() |
| 移動平均 | pandas の rolling_mean() |
| 乱数発生 | NumPy/SciPy が非常に強力、 R でも十分 |
| 順位と百分位数 | |
| 回帰分析 | Excel が簡単 |
| サンプリング | 任意の言語 |
| t 検定 | scipy.stats または R |
| z 検定 | scipy.stats または R |
t 検定に関しては以前も説明した通りウェルチの検定を使うのが筆者のオススメです。理由はリンク先の記事に挙げましたので省略しますが、分散が等しくないときの検定について等分散検定→等平均検定と二段階の検定をする古典的手法より簡単で正確かと思います。
カイ二乗検定も SciPy の関数が便利かと思います。
またデータのサンプリングや乱数生成なども NumPy/SciPy でおこなうとそのまま後続の処理に渡すことができますし、プログラミングもしやすいので断然オススメです。
回帰分析のように複雑で読み取りが必要なものは Excel のほうがわかりやすいかもしれません。処理結果をそのまま別の処理に入力させるといったこともあまり無いと思います。
このように Excel のほうがラクでわかりやすいものもありますし SciPy でデータを処理したほうが汎用的で使いやすいものもあります。無理にツールを統一しようとするよりは、用途に応じてそのつど向いているものを選択したほうが良いでしょう。適材適所というところです。
このあたりは筆者の主観ですので、分析者の最もやりやすいようにするのが良いかと思います。ツールや手法が重要なのではないということです。