前回までロジスティック回帰の話でしたが今日は因子分析の話です。
最初に掲げた一般化線形モデルの表を参照してください。
因子分析とは、複数の変数があったとき、その背後にそれらに影響する構成概念があるものと仮定し、少数の潜在的変数で複数の変数間の関係を説明しようというものです。
このように少数の変数へと変換することを縮約、またこの構成概念を説明する潜在的変数を因子と言います。因子分析は背後に共通した因子が想定できる変数を縮約し、新しい量的な変数を作ります。
このような伝統的な統計手法はすでに解説しているサイトがたくさんあります。たとえば次のページなども参考にしてください。
株式会社NTTデータ数理システム S+rescue Chap6 因子分析
http://www.msi.co.jp/splus/learning/rescue/factor.html
因子分析をやってみる
昨今では Python が機械学習やデータマイニングなどの分野で台頭していますが、古典的な統計分析手法に関してはやはり R 言語が豊富なライブラリ資産を抱えており充実しています。無理に Python を使わずここは R でやってみたいと思います。
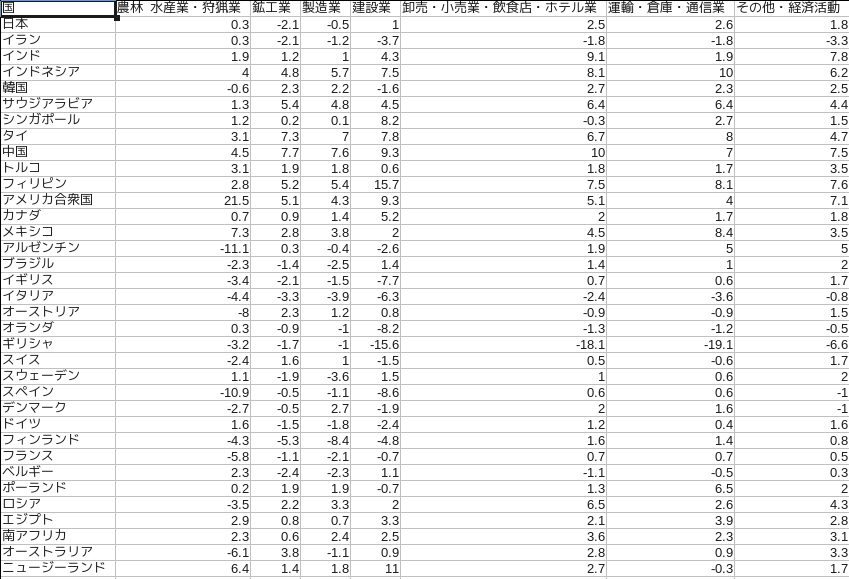
今回はサンプルデータとして総務省統計局の世界の統計 2014 から 3-5 国内総生産の実質成長率を利用しました。最近ではこのように統計のサンプルとしてちょっとした加工ですぐに利用できるデータがあちこちに公開されていますので何かと便利ですね。
データのイメージは以下の通りです。各国の 2012 年の GDP 成長率を抽出してあります。なお加工後のデータはこちらです。
因子分析ではあらかじめ因子数を与える必要があります。結果を 2 次元のバイプロットで表示したいので因子数は 2 としましょう。これは A と B という 2 つの何らかの独立した隠れた変数によって決まると仮説を立てたことになります。もちろん因子分析では 3 でも 4 でも好きなように因子数を与えることができます。
ソースコードは以下の通りです。なおこちらにソースコードを公開しています。
# CSV ファイルを読み込む
df = read.csv("sample_data.csv")
# 1 列目を列名にする
row.names(df) = df[,1]
# 2 〜 8 列目をデータフレームにする
df = df[,2:8]
par(xpd=TRUE)
# prcomp してバイプロットして可視化する
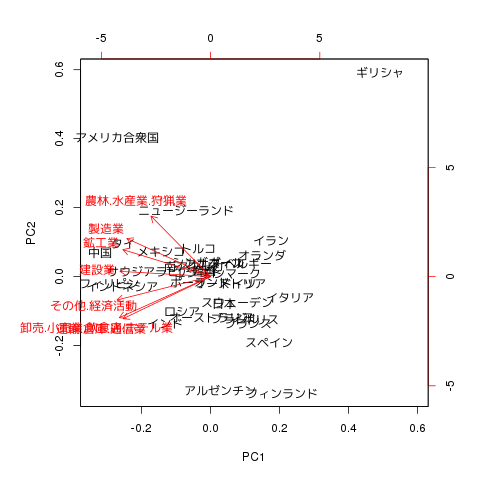
biplot(prcomp(df, scale=TRUE))
# factanal で因子数 2 で因子分析する
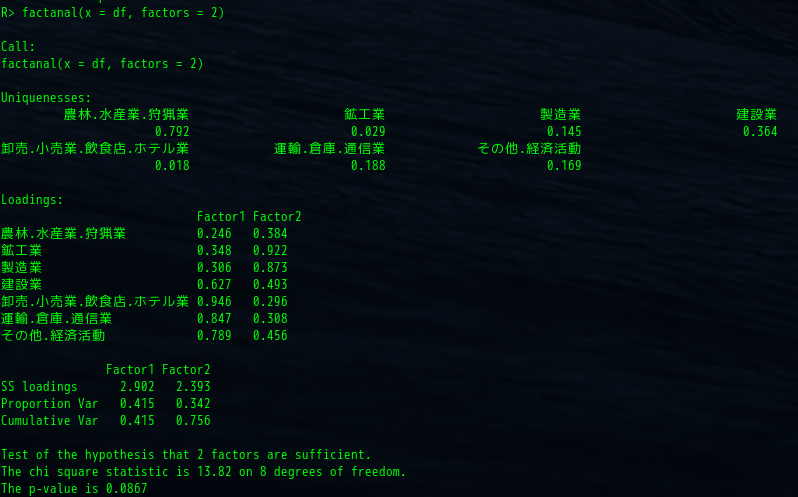
factanal(x = df, factors = 2)
まずはバイプロットの結果を見てみましょう。
PC1 (第一主成分) と PC2 (第二主成分) という二変数に分解できました。
また R での出力は次のようになります。
| 出力 | 意味 | 説明 |
|---|---|---|
| Uniquenesses | 独自性 | 各変数の潜在因子で説明できない部分 |
| Loadings | 因子負荷 | 観測変数に対して共通因子がどれくらいの強さで影響を与えているか |
| SS loadings | 因子寄与 | 因子負荷の平方和 |
| Proportion Var | 因子寄与率 (分散説明率) | その因子がデータをどれだけ説明できているか |
| Cumulative Var | 累積因子寄与率 | 因子分析した諸項目に対する因子の影響力 |
また各変数と因子空間との相関を共通性、各変数と各因子の相関を因子負荷量と言います。
出力の一番下は適合性の検定をおこなっています。これは 2 因子モデルが元のデータにあてはまっているかどうかということを指しています。
この場合ですとカイ二乗値は 13.82 、自由度は 8 、 p 値は 0.0867 となります。
また共通性を求めるには因子分析の独自性を 1 から引けば求まります。
共通性が高いということは、因子で説明できる部分が大きいということを意味しています。
主成分分析と因子分析の違い
主成分分析 (Principal Compotent Analysis) と 因子分析 (Factor Analysis) の差異はしばしば話題になります。
上に紹介したサイトでも少し触れられていますが、
主成分分析のモデルは
PC_i = l_{i1}X_1 + l_{i2}X_2 + ... + l_{in}X_n
であり観測変数を原因系として、合成変数として作られた主成分が結果系です。
これに対し因子分析のモデルは
Xi = 変数
λin = 因子負荷量
Fn = 因子
μi = 誤差 (独自因子)
とすると
X_i = \lambda_{i1}F_1 + \lambda_{i2}F_2 + ... + \lambda_{in}F_n + \mu_i
であり、主成分が結果変数である主成分分析と比較すると、因子が原因変数である因子分析は因果関係を異にすると言えます。
まとめ
今回は因子分析の話をしました。次回に続きます。