前回はロジスティック回帰について、概要について参考文献を紹介、使いどころと使用例を説明しました。
前回も述べた通り、ロジスティック回帰とは二値論理と言われる true か false かという論理に関するアウトカムを分析するための方法です。
今日は実際にオリジナルのデータを使ってロジスティック回帰分析をし、その結果について考察してみたいと思います。
想定するシナリオ
今回は話をわかりやすくするためにオンラインゲームを想定します。
あるオンラインゲームでは毎月イベントがあります。このイベントではフレンド同士で協力して戦ってスコアを稼ぎます。そして、スコアが高い上位ランキング 1,000 位以内に入ると特別な報酬が貰えます。
前回の実績となる数名のユーザーのデータを集めたので、ここからランキング上位に入賞するための成功要因を分析したいと思います。
いかがでしょうか。わかりやすくするためにゲームを例に挙げましたが、たとえば「営業マンが契約を取ってこれるかどうか」「顧客が商品を買ってくれるかどうか」などいろいろなビジネスケースが考えられると思います。
ここで結論を述べる 1 つの結果は true か false という質的な二値のアウトカムでとらえることができます。今回の例で言うと「ランキングに入賞したかどうか」です。
モデルの入力と出力
ここでインプットとアウトプットを整理します。
入力 : 対戦レベル、パーティー全体の攻撃力、フレンドの数、張り付いている時間……
出力 : ランキング上位 1,000 位以内に入れるか (0 〜 1 の値)
このように true か false に分類する問題を扱う方法を識別モデルと言います。
代表的な識別モデルとしては、今回使うロジスティック回帰のほかに、決定木、ランダムフォレスト、ニューラルネットワーク、 SVM (サポートベクトルマシン) などが挙げられます。
今回はこの中から王道とも言えるロジスティック回帰を選択したわけです。ロジスティック回帰では、アウトカムに対する説明変数が 1 つであろうが複数であろうが区別をしません。つまり上記のように、レベルやら攻撃力やらフレンドの数やら……と説明変数が多岐にわたっても分析ができます。
分析対象のサンプルデータ
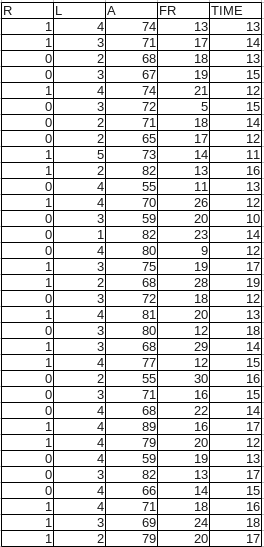
データ項目は次の通りとします。
R = 結果としてランキング 1,000 位以内に入れたかどうか (1 = 入れた)
L = 対戦レベル (上位ほどスコアにボーナス倍率が付く)
A = パーティー全体の攻撃力、 50 万なら 50 とする
FR = 毎日支援してくれるフレンドが何人いるかその人数
TIME = 1 日何時間そのオンラインゲームに張り付いてプレイしているか
データの内容は次の通りとします。
ロジスティック回帰の方法
R の場合、ロジスティック回帰そのものは簡単です。次のようにします。
# データの読み込み
data <- read.csv("sample_data.csv", header=TRUE)
# ロジスティック回帰
result = glm(R ~ L + A + FR + TIME, data=data, family=binomial(link="logit"))
# 結果の表示
summary(result)
本来はデータ加工の前処理やチューニングなどを挟むのですが省略します。
R で得られるサマリー出力は以下のようなものとなります。
Call:
lm(formula = R ~ L + A + FR + TIME, data = data)
Residuals:
Min 1Q Median 3Q Max
-0.74571 -0.34436 0.08457 0.26984 0.67838
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.866380 0.931936 -4.149 0.000282 ***
L 0.258382 0.085172 3.034 0.005168 **
A 0.030380 0.009641 3.151 0.003851 **
FR 0.045191 0.013705 3.297 0.002659 **
TIME 0.037038 0.035000 1.058 0.298997
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3984 on 28 degrees of freedom
Multiple R-squared: 0.4607, Adjusted R-squared: 0.3837
F-statistic: 5.98 on 4 and 28 DF, p-value: 0.001311
このうち重要なのは Pr(>|t|) として表示される「有意確率」です。有意確率とは統計的仮説検定において、帰無仮説のもとで得られた検定統計量が実現する確率のことです。有意確率の小さい順に採用変数の重要度を採択します。
オッズ比を求める
さらにオッズ比を求めます。これは 1 上がるとその他比で確率が何倍になるかという値です。
# names() とすると、オブジェクトにどのような係数が格納されているか一覧が表示される
names(result)
# =>
# [1] "coefficients" "residuals" "fitted.values" "effects" "R" "rank"
# [7] "qr" "family" "linear.predictors" "deviance" "aic" "null.deviance"
# [13] "iter" "weights" "prior.weights" "df.residual" "df.null" "y"
# [19] "converged" "boundary" "model" "call" "formula" "terms"
# [25] "data" "offset" "control" "method" "contrasts" "xlevels"
# オッズ比としては coefficients を見ますので以下のように指定します
exp(result[[1]])
# => (Intercept) L A FR TIME
# 6.848829e-17 7.383491e+00 1.318194e+00 1.449996e+00 1.322353e+00
# ↑これがそれぞれの説明変数のオッズ比となります。
分析結果と考察
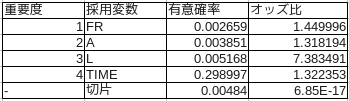
こうしてロジスティック回帰分析の結果が求まりました。次の表にまとめます。
意外なことに、このオンラインゲームのイベントではフレンド (FR) が最も重要な要素であることがわかりました。
つまり、パーティー全体の攻撃力を上げることも、対戦レベルを上げることも当然ながら大切なのですが、実際には常時支援してくれるフレンドがたくさんいるということがランキング上位入賞の決め手となることがわかりました。また逆に、ゲームに張り付いている時間が長いかどうかはそこまで重要では無さそうです。
このように分析できましたから、もし攻撃力とレベルがすでにそれなりなのであれば、飽和状態の高い攻撃力をさらに高めるために追加課金して強いアイテムを揃えようとしたり、あるいは対戦レベルを高めるために無理して対戦して消耗したりするというのはほどほどにして、協力的なフレンドをいかに集めてイベントに挑むかという部分に注力したほうがより効率的であると言えるでしょう。
ロジスティック回帰分析によってあまり効果的でない課金を回避して、勝負のどこに注力したら良いかを数値的に判断できるようになったというわけです。このように緻密に分析していけばより少ない投資額で効率的に勝負を勝ち抜けそうですね。
さて、今回はオンラインゲームを例にしましたが、実際のビジネスにおいてもこのように多岐に渡る説明変数から重要なファクターを拾い上げるための手がかりとして使えそうだということがおわかりになったのではないでしょうか。たとえば商談を成功させるために決め手となる要因を導き出したり、商品が売れるための決め手となる手がかりを見つけ出したりといった場面でもロジスティック回帰分析が威力を発揮します。
ロジスティック回帰分析の話はこれでおしまいです。次回に続きます。