2 つの変量の関係を調べる (2) #Python

今日はキッチンに立って炒めたキャベツの中華スープを作ろうと思います。よくかき混ぜてから、ほんのひとくち味見をして、料理の出来を判断します。

あるいは、会社の採用面談において、ほんの数十分の顔合わせでその人が社員にふさわしいかどうかを判断したりします。

もしくは、ほんの数カ月あるいは一年程度の交際で、その後ずっと一生連れ添う相手として結婚を決意したりします。

このように、一部の標本から母集団を推測することこそ、推測統計の極意なのです。

標本抽出

2 つの変量を選択するにあたり、標本を母集団から抽出することになります。以前も説明した通り標本抽出法にはさまざまな種類があります。

前回の例では、ある高校生のクラスの 10 名に注目してスポーツの成績を抽出しました。

これで高校生全体の成績が立ちどころにわかるというわけではありません。しかし、このような標本の統計的な情報から全体をある程度の正確性で推測することが可能になるわけです。つまり標本の抽出はそれ自体が目的なのではなく、全体を把握するための手段というわけなのです。

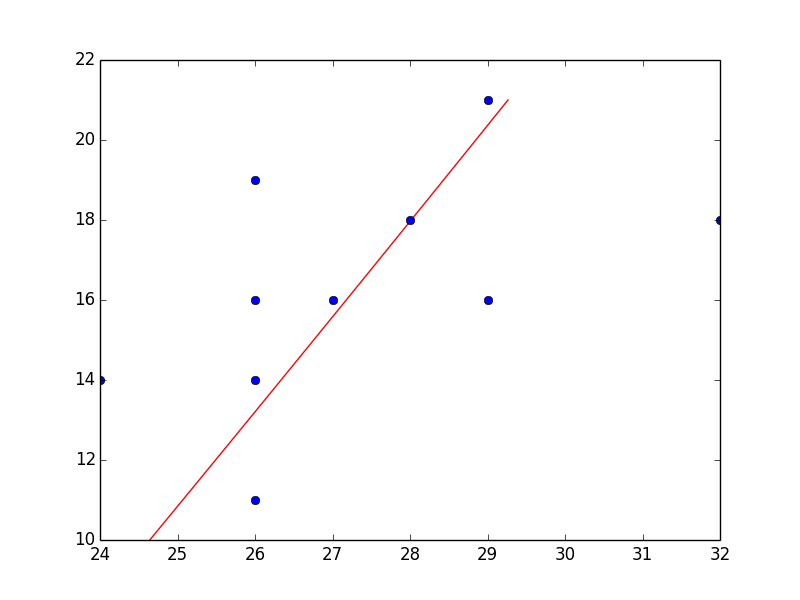
前回の例で、握力と珠投げの関係はいくぶんか右上がりに分布しているように見えました。

そしてその相関係数は 0.53 でした。多少の正の相関があることになります。

相関係数 r(x,y) の値は -1 から 1 の範囲となり絶対値 1 に近いほど相関の程度が強くなります。

ここであらためて 2 つの変量 x,y について考えてみます。

項目	値
変量 x	x_1, x_2, ..., x_n
変量 y	y_1, y_2, ..., y_n

変量 x,y の相関図で、中心 O'(x,y) を通る直線

y=a(x-\overline{x})+\overline{y}

のうち N 個の点

P_1(x_1,y_1), P_2(x_2,y_2), ... P_N(x_N,y_N)

に一番近い直線を考えてみましょう。

y の x への回帰直線は次のとおりになります。

\frac {y-\overline{y}} {\sigma(y)} = r(x,y) \frac {x-\overline{x}} {\sigma(x)}

線形回帰については以前も説明しました。最小二乗法についてもう一度思い出してみましょう。

相関係数が 1 に近くなると (r(x,y) → 1), 上の S_0 → 0 となりますから、散布図のすべての点はしだいに直線に近い形で分布していくことになるわけです。