相関係数を調べる
データの分析においてまず基本となるのは興味あるデータを収集することです。統計学の関心はあくまでも全体の状況や傾向であり、それを知る基本は分布のモデルと統計量 (平均や分散) です。
相関係数を調べることは基本中の基本です。以前も線形回帰や相関係数の話はさんざんしましたが、ここでさらに紐解いて詳細を探っていきましょう。
データを集めて図にする
あるスポーツをするにあたり、高校生のボール投げと握力の値を調べてみました。
| 生徒 | 握力 | 球投げ |
|---|---|---|
| A | 26 | 16 |
| B | 26 | 11 |
| C | 26 | 14 |
| D | 27 | 16 |
| E | 28 | 18 |
| F | 29 | 16 |
| G | 32 | 18 |
| H | 29 | 21 |
| I | 24 | 14 |
| J | 26 | 19 |
何度も繰り返すようですが、統計とはまずデータ収集にはじまります。今回の例では生徒個人個人のスポーツの成績を記録し表にしてみました。しかし表だけでは関係がよくわかりません。そこで図にしてみます。二つの変量 x と y のあいだにどのような関係があるか、これは散布図を描くことによっておおまかな傾向をつかむことができます。
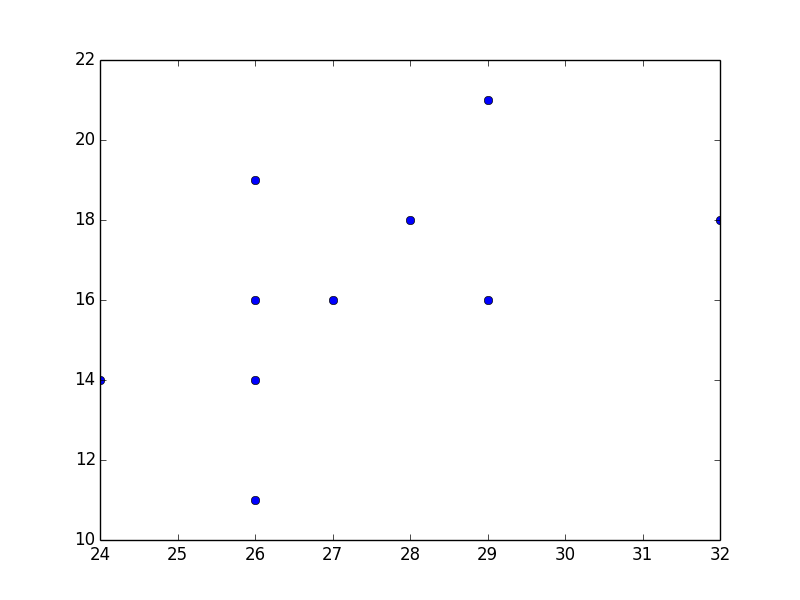
ではさっそく今までに学んだ知識を生かして散布図を描いてみましょう。
import numpy as np
import matplotlib.pyplot as plt
X = np.array( [26, 26, 26, 27, 28, 29, 32, 29, 24, 26] )
Y = np.array( [16, 11, 14, 16, 18, 16, 18, 21, 14, 19] )
plt.plot(X, Y, 'o', color="blue")
plt.show()
plt.savefig("image.png")
なんとなく正の相関がありそうです。
相関係数を求める
これも散々今まで説明してきましたが、次に知りたいのは 2 つの変量 x,y の関係の強弱を数値化して調べることです。これが相関係数です。
相関係数の具体的な計算としては、次の共分散を求める公式を利用します。
Cov(x,y) = \frac 1 N \sum_{k=1}^N X_kY_k - \overline{x} \overline{y}
思い出しましたか。相関係数は次のように求まります。
r(x,y) = \frac {Cov(x,y)} {\sigma(x)\sigma(y)}
したがって
r(x,y) = \frac {10 * 4481 - 273 * 163} {\sqrt{(10*7499-273^2)(10*2731-163^2)}} = 0.53
となります。
果たしてこの手計算は正しいでしょうか。これもコードを書いて実際に試してみましょう。
corr = np.corrcoef(X, Y)[0,1]
print("X と Y の相関係数は %(corr)s" %locals() )
# => X と Y の相関係数は 0.532109266822
さすが NumPy です。たった 1 行のコードで答えが求まりました。
まとめ
統計の基本ともいえる 2 つの変量の関係についてもう一度復習をはじめました。今回は手始めに散布図と相関係数を求めました。