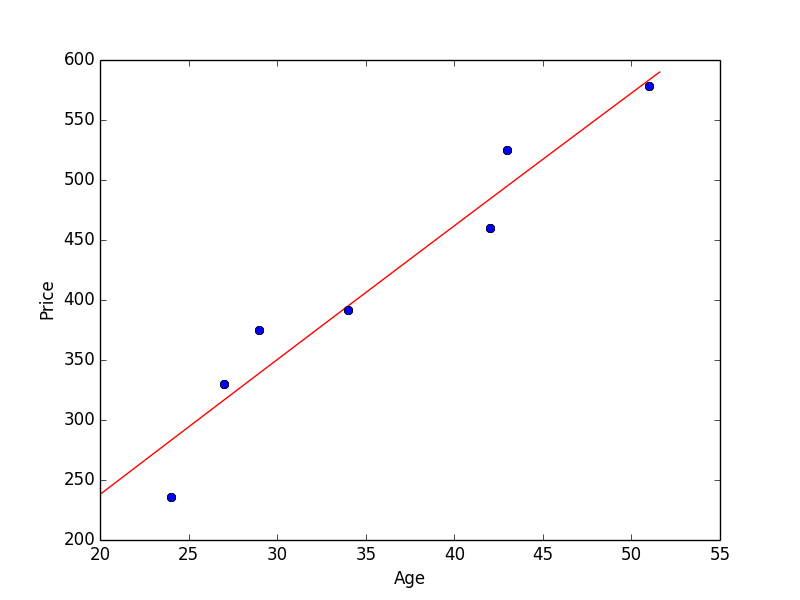
連続変数が 2 つ存在するとき、この関連性を検討する場合は 散布図 (scatter plot) を描きます。これまで説明してきた通り散布図を描くためには matplotlib や R といったツールが有用です。
線形回帰再訪
線形回帰と相関係数の回で取り上げましたから復讐してみましょう。
import numpy as np
import matplotlib.pyplot as plt
# 2 つの連続変数
v1 = np.array([24, 27, 29, 34, 42, 43, 51])
v2 = np.array([236, 330, 375, 392, 460, 525, 578])
def phi(x): # ファイ係数を算出する、この場合は X=4
return [1, x, x**2, x**3]
def f(w, x): #
return np.dot(w, phi(x))
PHI = np.array([phi(x) for x in v2])
w = np.linalg.solve(np.dot(PHI.T, PHI), np.dot(PHI.T, v1))
ylist = np.arange(200, 600, 10)
xlist = [f(w, x) for x in ylist]
plt.xlim(20, 55)
plt.ylim(200, 600)
plt.xlabel('Age')
plt.ylabel('Price')
plt.plot(v1, v2, 'o', color="blue")
plt.plot(xlist, ylist, color="red")
plt.show()
plt.savefig("image.png")
連続変数の統計量は次のように求まります。これも過去の記事にありましたね。
| 項目 | 関数 | 値 |
|---|---|---|
| v2 の平均 | np.average(v2) | 413.714285714 |
| v2 の分散 | np.var(v2) | 11725.3469388 |
| v2 の標準偏差 | np.std(v2) | 108.283641141 |
| v1 と v2 の相関係数 | np.corrcoef(v1, v2) | 0.96799293 |
変数 X (= v1) が増加すれば Y (= v2) も増加する というとき、正の相関と言います。この場合は正の相関があると言えます。
線形関係と相関係数
このように、ひとつの変数が変化すれば、もうひとつの変数も変化するという単調な変化を示すとき、この直線的な関係のことを 線形関係 (linear relationship) と言います。
相関係数とは正確には ピアソンの積率相関係数 (Pearson's product moment correlation coefficient) と言います。相関係数というのは他にも一応あるのですが、一般的にはこのピアソンの積率相関係数を指すことがほとんどです。
また散布図を作成したとき、この直交座標系の右上を第 1 象限と言います。同様に左上は第 2 象限、左下は第 3 象限、右下は第 4 象限と言います。散布図全体として第 1 象限と第 3 象限に分布が多い場合は偏差の積の合計値が正の方向に大きいとなるわけです。
共分散 (covariance) という数値は連続変数同士の線形関係の強さと方向を示す数値であり、次の式で示されます。
Cov(X, Y) = \frac {\sum (Y_i - \overline{Y})(X_i - \overline{X})} {N - 1}
積率相関係数は共分散を使い X と Y の標準偏差 σ で補正することで算出できます。
r_{xy} = \frac {Cov(X, Y)} {X の \sigma × Y の \sigma}
まとめ
相関係数についてあらためて整理し補足しました。 2 変数間にまったく線形関係がないという帰無仮説をたてたとき、積率相関係数の検定が必要となります。この場合、帰無仮説では母相関が 0 であり、ひとつの変数の値が変わっても他方の変数の値が変化しない独立の状態を仮定します。標本データについて独立の状態からの解離度合いから、母集団における相関係数が 0 かそうでないかを検定するわけです。
参考
社会統計学入門
http://www.amazon.co.jp/dp/4595313705
ベイズ線形回帰を実装してみよう
http://gihyo.jp/dev/serial/01/machine-learning/0014