線形回帰と相関係数、そして東京の平均気温を実際に分析してみる

線形回帰における仮定

前々回、前回 と線形回帰について説明してきました。

線形回帰における最小二乗法では Y 軸の点と点の全体的な長さの差異 (= これを、それぞれの差の二乗を取ってから加算するので二乗誤差といいます) が最小になるように、まっすぐな線 (= 1 次式の直線となる関数) を求めました。すなわち、データの集合から直線に回帰する推定をおこなったわけです。

相関係数を求める

どんな 2 次元データでも線形回帰で関数を導くことはできますが、それが妥当かどうか気になります。そこで両者の相関係数を求めます。相関係数はベクトル v1, v2 からそれぞれの要素 x, y の平均を求め、次に v1, v2 の分散と共分散を求めます。コードで表現してみましょう。

def correlation(data):
    n = len(data) # 二次元データの長さを n に求める
    xm = 0.0
    ym = 0.0
    for x, y in data:
        xm += x
        ym += y
    xm /= n # x の平均を xm に求める
    ym /= n # y の平均を ym に求める
    sx2 = 0.0
    sy2 = 0.0
    sxy = 0.0
    for x, y in data:
        sx2 += (x - xm) ** 2 # x の分散を sx2 に求める
        sy2 += (y - ym) ** 2 # y の分散を sy2 に求める
        sxy += (x - xm) * (y - ym) # 共分散 sxy を求める
    return sxy / math.sqrt(sx2 * sy2) # 共分散 sxy をそれぞれの分散の乗算の平方根で除算

たかだか相関係数を求めるためにだいぶ長いコードになってしまいました。毎回こんなコードを実装していられませんからここで数学関数ライブラリの出番となります。 NumPy は数理計算の基礎となる強力なライブラリで、標準的な数学関数、行列計算、乱数生成、フーリエ変換などの豊富な機能を提供してくれます。これを使えば相関係数が簡単に求められます。

import numpy as np
np.corrcoef(v1, v2)

簡単ですね。
相関係数の説明は一般的に次のようになります。

絶対値	説明
0.7 <= x < 1.0	強い相関
0.4 <= x < 0.7	中程度の相関
0.2 <= x < 0.4	弱い相関
0.0 <= x < 0.2	ほぼ相関なし

また、値が正なら正の相関、負なら負の相関があると言います。

前々回の例題から相関係数を求めると 0.96799293 となりました。強い正の相関があることになります。

このように強い相関がある場合は求まる関数は直線つまり 1 次式で良さそうですが、実際のデータではなかなかそのようなわかりやすい例を導くのは難しそうです。線形回帰のように仮定を前提とした考え方は結局の決めの問題で、どのような関数を導くのが最も良いのかはケースバイケースと言えるでしょう。

そこで多項式基底の線形回帰を考えます。基底関数には複数の多項式を仮定し、求めたい関数 f(x) はその線形和として表現できます。パラメータを選ぶ指標としては二乗誤差を用います。

さまざまな相関係数の例

ではそれぞれの相関を例として挙げてみましょう。

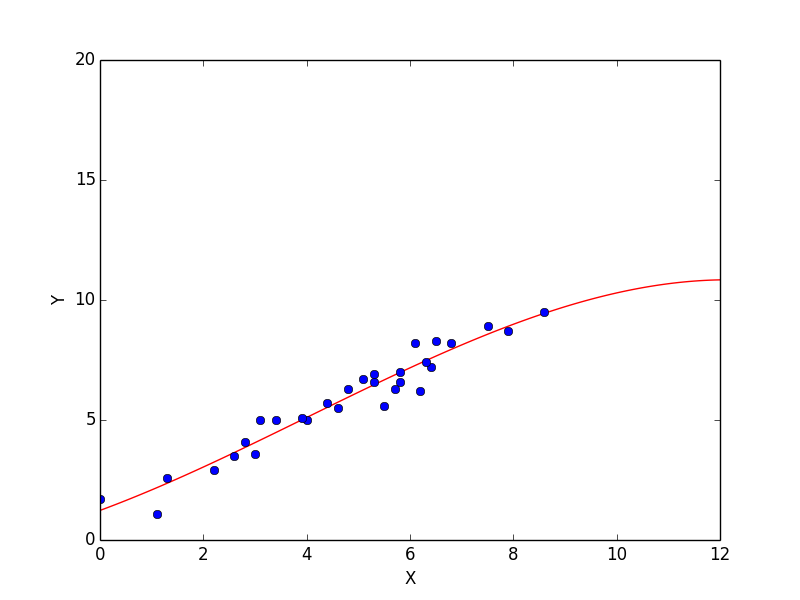
強い正の相関

元データ

v1 = [4.6, 0.0, 6.4, 6.5, 4.4, 1.1, 2.8, 5.1, 3.4, 5.8, 5.7, 5.5, 7.9, 3.0, 6.8, 6.2, 4.0, 8.6, 7.5, 1.3, 6.3, 3.1, 6.1, 5.3, 3.9, 5.8, 2.6, 4.8, 2.2, 5.3]
v2 = [5.5, 1.7, 7.2, 8.3, 5.7, 1.1, 4.1, 6.7, 5.0, 6.6, 6.3, 5.6, 8.7, 3.6, 8.2, 6.2, 5.0, 9.5, 8.9, 2.6, 7.4, 5.0, 8.2, 6.6, 5.1, 7.0, 3.5, 6.3, 2.9, 6.9]

線形回帰

相関係数は 0.96841872 です。強い正の相関があることが一目でわかりますね。

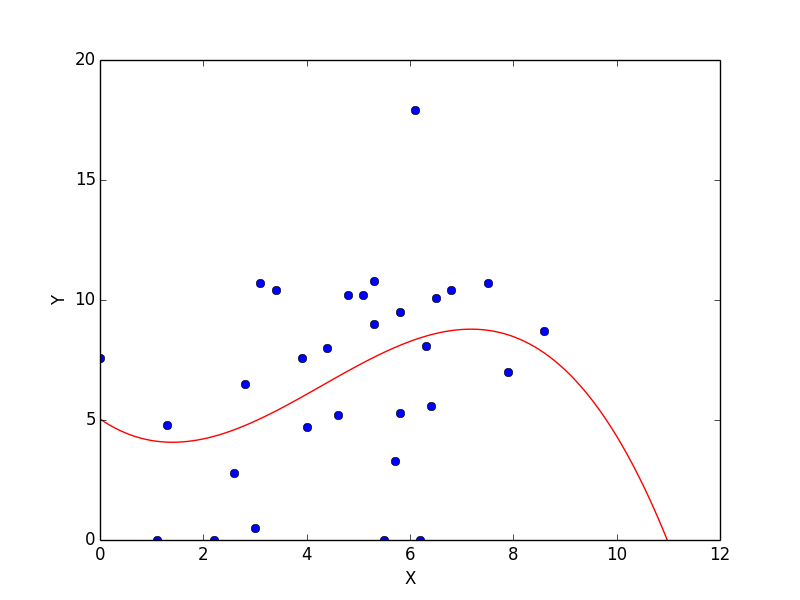
弱い正の相関

元データ

v1 = [4.6, 0.0, 6.4, 6.5, 4.4, 1.1, 2.8, 5.1, 3.4, 5.8, 5.7, 5.5, 7.9, 3.0, 6.8, 6.2, 4.0, 8.6, 7.5, 1.3, 6.3, 3.1, 6.1, 5.3, 3.9, 5.8, 2.6, 4.8, 2.2, 5.3]
v2 = [5.2, 7.6, 5.6, 10.1, 8.0, 0.0, 6.5, 10.2, 10.4, 5.3, 3.3, 0.0, 7.0, 0.5, 10.4, 0.0, 4.7, 8.7, 10.7, 4.8, 8.1, 10.7, 17.9, 9.0, 7.6, 9.5, 2.8, 10.2, 0.0, 10.8]

線形回帰

相関係数は 0.35231303 です。やや右肩上がりですが、それほど強い相関ではないようですね。

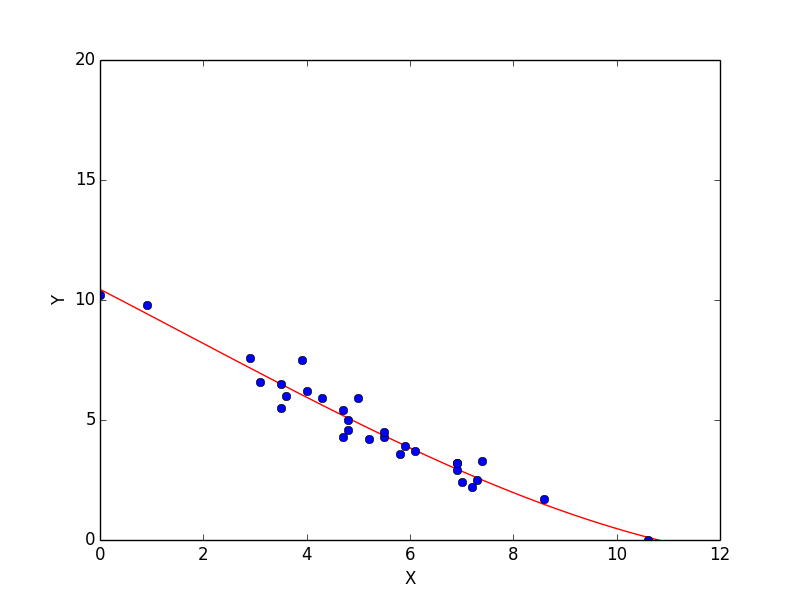
強い負の相関

元データ

v1 = [6.1, 3.9, 8.6, 5.9, 3.5, 7.0, 0.9, 0.0, 5.2, 3.5, 6.9, 4.3, 5.0, 7.4, 3.1, 4.0, 6.9, 4.8, 10.6, 4.7, 2.9, 7.2, 3.6, 5.5, 5.5, 6.9, 5.8, 4.8, 7.3, 4.7]
v2 = [3.7, 7.5, 1.7, 3.9, 5.5, 2.4, 9.8, 10.2, 4.2, 6.5, 3.2, 5.9, 5.9, 3.3, 6.6, 6.2, 2.9, 5.0, 0.0, 4.3, 7.6, 2.2, 6.0, 4.3, 4.5, 3.2, 3.6, 4.6, 2.5, 5.4]

線形回帰

相関係数は -0.96964376 です。強い負の相関があることが一目でわかります。

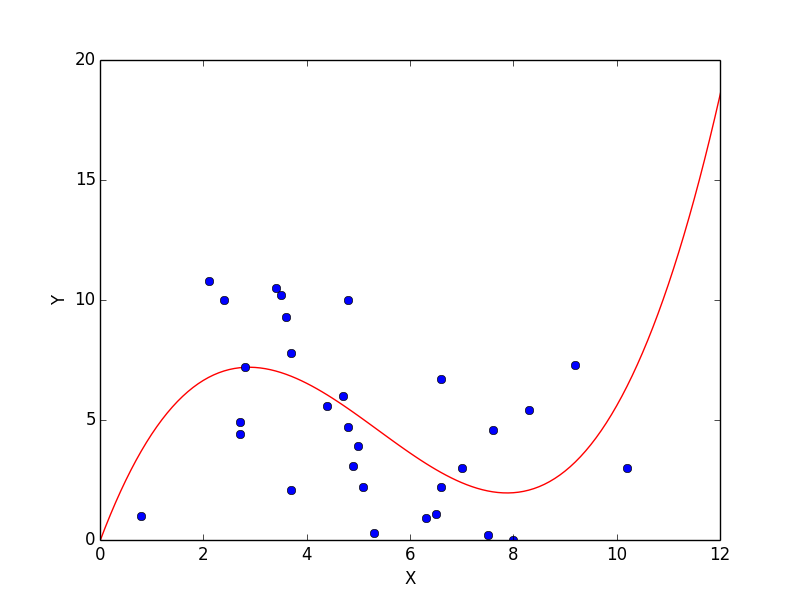
弱い負の相関

元データ

v1 = [3.5, 8.0, 10.2, 2.1, 2.8, 3.7, 5.1, 7.5, 7.6, 5.3, 4.7, 8.3, 4.8, 6.6, 2.4, 4.4, 3.6, 7.0, 4.9, 2.7, 9.2, 3.7, 0.8, 4.8, 6.5, 6.3, 2.7, 5.0, 3.4, 6.6]
v2 = [10.2, 0.0, 3.0, 10.8, 7.2, 2.1, 2.2, 0.2, 4.6, 0.3, 6.0, 5.4, 4.7, 2.2, 10.0, 5.6, 9.3, 3.0, 3.1, 4.4, 7.3, 7.8, 1.0, 10.0, 1.1, 0.9, 4.9, 3.9, 10.5, 6.7]

線形回帰

相関係数は -0.38354127 です。やや右下がりになっているように見えます。

本物の気象観測データで線形回帰をする

気象庁では過去の気象データ検索として毎年の気温などのデータが公開されています。ここでは 1970 年から 2013 年までの東京の平均気温を利用して回帰を用いて推定をしてみます。

まずは気象庁のもとのデータを表にしてみました。 40 年あまりのデータなので、だいぶ長い表になってしまいました。

年	東京の平均気温
1970	15.2
1971	15.0
1972	15.7
1973	15.7
1974	15.2
1975	15.6
1976	15.0
1977	15.8
1978	16.1
1979	16.9
1980	15.4
1981	15.0
1982	16.0
1983	15.7
1984	14.9
1985	15.7
1986	15.2
1987	16.3
1988	15.4
1989	16.4
1990	17.0
1991	16.4
1992	16.0
1993	15.5
1994	16.9
1995	16.3
1996	15.8
1997	16.7
1998	16.7
1999	17.0
2000	16.9
2001	16.5
2002	16.7
2003	16.0
2004	17.3
2005	16.2
2006	16.4
2007	17.0
2008	16.4
2009	16.7
2010	16.9
2011	16.5
2012	16.3
2013	17.1

さて、この表をぼーっと眺めていても人間の感覚ではとくに何となく読み取れる感じがしませんし時間のムダですね。さっそく統計分析に取りかかります。まずはデータをリストと呼ばれる形式にします。

[15.2, 15.0, 15.7, 15.7, 15.2, 15.6, 15.0, 15.8, 16.1, 16.9, 15.4, 15.0, 16.0, 15.7, 14.9, 15.7, 15.2, 16.3, 15.4, 16.4, 17.0, 16.4, 16.0, 15.5, 16.9, 16.3, 15.8, 16.7, 16.7, 17.0, 16.9, 16.5, 16.7, 16.0, 17.3, 16.2, 16.4, 17.0, 16.4, 16.7, 16.9, 16.5, 16.3, 17.1]

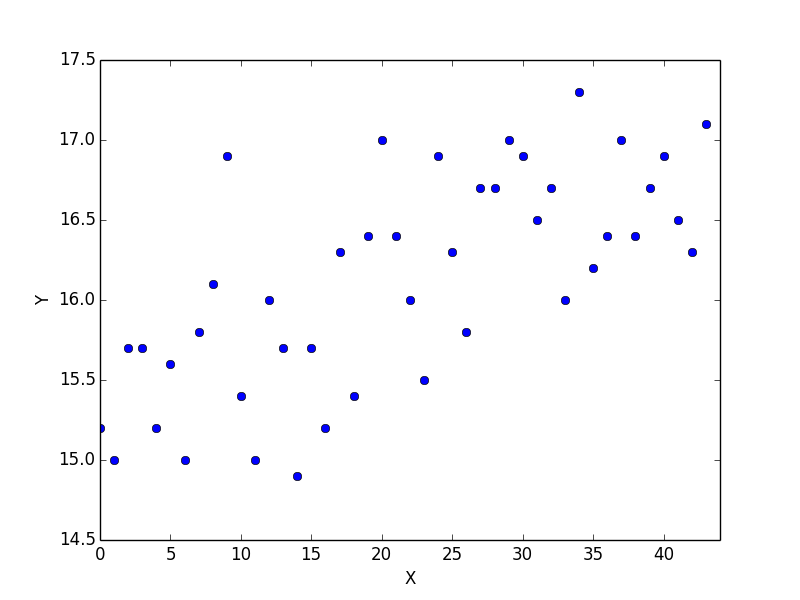
matplotlib で散布図にプロットしてみます。

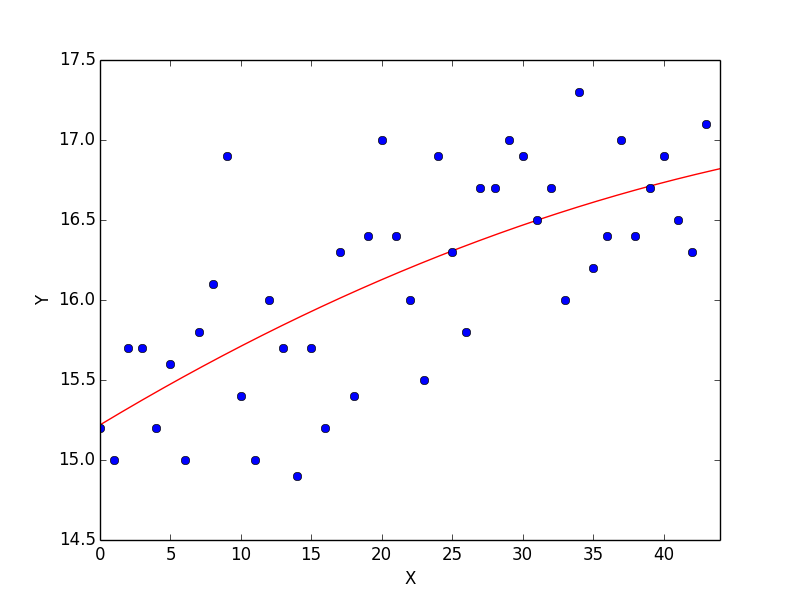
さらに二乗誤差を求めて線形回帰します。

このときの相関係数は 0.69914461 になりました。そこそこの正の相関が見られるようです。この 40 年ほどで東京の平均気温は着実に上昇してきつつあるということが統計的に分析できました。