人工知能の積年の目標は、挑戦的な分野において、「白紙の状態」から人間を超越した技能を習得するアルゴリズムである。
A long-standing goal of artificial intelligence is an algorithm that learns, tabula rasa, superhuman proficiency in challenging domains. ー D. Silver
この記事の内容をざっくり3行で:
- FizzBuzzをニューラルネットワークにゼロから学習させる
- 強化学習で徐々に正確な文字列を出力できるようにする
- 10分でFizzBuzzを完全に理解できた
目次:
FizzBuzz とは
FizzBuzzとは英語圏におけるパーティーゲームで、Wikipediaによれば
最初のプレイヤーは「1」と数字を発言する。次のプレイヤーは直前のプレイヤーの次の数字を発言していく。ただし、3で割り切れる場合は「Fizz」、5で割り切れる場合は「Buzz」、両者で割り切れる場合(すなわち15で割り切れる場合)は「Fizz Buzz」を数の代わりに発言しなければならない。発言を間違えた者や、ためらった者は脱落となる。
単純ですが、実際にやってみたら結構難しそうです。
実際の進行例としては次のようになります。
1, 2, Fizz, 4, Buzz, Fizz, 7, 8, Fizz, Buzz, 11, Fizz, 13, 14, FizzBuzz, 16, 17, Fizz, ...
プログラム問題としての知名度が高いかと思います。コードが書けないプログラマを見分ける方法として Jeff Atwoodが提唱した ものです。
1から100までの数をプリントするプログラムを書け。ただし3の倍数のときは数の代わりに「Fizz」と、5の倍数のときは「Buzz」とプリントし、3と5両方の倍数の場合には「FizzBuzz」とプリントすること。
プログラミング初心者でも標準出力とループ処理と条件分岐が理解できていれば難しくありません。
例えばPythonで書くなら
for i in range(1, 101):
if i % 15 == 0:
print("FizzBuzz")
elif i % 3 == 0:
print("Fizz")
elif i % 5 == 0:
print("Buzz")
else:
print(i)
プログラム問題としてあまりにも有名になってしまったので、今ではあらゆる言語のFizzBuzzがそろっています。面白いですね。
深層学習 で FizzBuzz
この記事の読まれている大半の方は、FizzBuzzを書くのにあまり苦労しないでしょう。
しかし、あなたが何かの拍子でプログラムの書き方を忘れてしまったらどうでしょう?
心配する必要はありません。そういうときこそAIの出番です。
最近は空前の人工知能ブームで、猫も杓子もDeep Learningです。
実際、Deep LearningによるFizzBuzzは、いくつも先例があります。
実装方法にはバリエーションがありますが、基本的には
- 入力は直前の数値 or 文字列
- 出力は「数値」「Fizz」「Buzz」「FizzBuzz」の4つ
- 訓練用の教師データを(例えば101〜10000の区間で)用意して学習する
といった方針みたいです。
最終的な正答率は**95〜97%**程度になるようです。
しかし、あなたの代わりにFizzBuzz問題を任せるには十分とは言えません。
職業的プログラマなら、100個中3つも誤った出力を出すようではクビになってしまうかもしれません。
そもそも、これらのネットワークを学習させるには正確な訓練用の教師データを人間側で用意する必要があります。
とはいえ、何万ものFizzBuzz文字列を手入力するのはおすすめできません。
自分でFizzBuzzプログラムが書けない場合はどうしたらよいのでしょう?
「人間の知識」を前提としないで、FizzBuzz問題に対処することは可能でしょうか?
AlphaGo Zero
「Deep Learningの代表的な成果を3つあげてください」
と聞かれたとき、あなたはどう答えますか? 少なくない方が**「囲碁」**を含めるのではないでしょうか。
「AlphaGo」はGoogle傘下のDeepMind社が開発した囲碁プログラムで、Deep Learningを駆使することで、今後10年はかかると言われていた人間のトッププレイヤー超えを実現しました。
そして2017年に発表された「AlphaGo Zero」はさらに衝撃を与えました。人間の知識を全く用いずに、「ゼロ」から囲碁を学習し、3日で人間を遥かに上回る実力を手にしてしまいました。
AlphaGo Zeroで用いられているドメイン知識は、基本的な囲碁のルールを除いて、
- 各局面での合法手
- 終了条件
- 終了局面でのスコア
など最低限のものしか利用していません。これまでの(初代のAlphaGoを含めて)囲碁のプログラムには様々な形で人間の知識(棋譜など)が用いられていたのですが、これらは必要ではなかったのです。AlphaGo Zeroはその後チェスや将棋にも応用され、それぞれの最強プログラムを圧倒する実力を見せています。
非常に素晴らしい成果です。
これを使えば人間の知識をあてにせずともFizzBuzz問題をクリアできそうです。
FizzBuzz の対戦ルール
いよいよ本題です。ゼロからFizzBuzzを学習させていきましょう。
その前に、FizzBuzzのゲームとしてのルールを整理します。冒頭の説明から
- N人のプレイヤーが順番に「数値」または「Fizz」「Buzz」「FizzBuzz」を選択する
- M回間違えたらそのプレイヤーは負け(=ゲームから脱落、報酬-1)
- 最後まで残っていたプレイヤーが勝ち(報酬+1)
問題を簡単にするため、プレイヤー数をN=2、失格になる回数はM=1としましょう。
これで「二人零和有限確定完全情報ゲーム」となり、将棋や囲碁と同じ扱いになりました。
加えて、FizzBuzz問題のために、以下の知識を与えることにしましょう。
- どちらも間違えずに100まで達したら引き分け(報酬0)
これで囲碁のときと同様、合法手、終了条件、スコア(勝敗)の情報が揃いました。
ネットワークモデル と 探索
まず、学習させるネットワークモデルを構築する必要があります。PythonとTensorFlowで実装していきます。
入力される情報はあまり多くても大変なので直前の10個としましょう。
時系列データなのでRNNやLSTMなどを使うのが自然ですが、今回は簡単に中間1層の全結合ネットワークです。
出力はAlphaGo Zeroと同様、
- 次の回答の予想確率分布 (policy)
- 現在の評価値 (value)
の2種類を同時に計算させておきましょう。
LAYER_CNT = 1
FEATURE_SIZE = 4
HISTORY_SIZE = 10
INPUT_SIZE = HISTORY_SIZE * FEATURE_SIZE
def model(self, x, temp=1.0, is_train=False):
h_fc = [tf.reshape(x, [-1, INPUT_SIZE]), ]
# fully connected layers
for i in range(LAYER_CNT):
# [-1, 10 * 4] => [-1, 10 * 4]
with tf.variable_scope('fc%d' % i):
h_fc.append(self.fully_connected(
h_fc[i], INPUT_SIZE, apply_relu=True,
batch_norm=(i != 0), is_train=is_train))
# policy connection
with tf.variable_scope('pc'):
# 1st layer
# [-1, 10 * 4] => [-1, 4]
h_pc = self.fully_connected(
h_fc[LAYER_CNT], FEATURE_SIZE, apply_relu=False,
batch_norm=True, is_train=is_train)
# divided by softmax temp and apply softmax
policy = tf.nn.softmax(tf.div(h_pc, temp), name="policy")
# value connection
with tf.variable_scope('vc'):
# 1st layer
# [-1, 10 * 4] => [-1, 1]
h_vc = self.fully_connected(
h_fc[LAYER_CNT], 1, apply_relu=False,
batch_norm=True, is_train=is_train)
# apply hyperbolic tangent
value = tf.nn.tanh(tf.reshape(h_vc, [-1]), name="value")
return policy, value
ついでに探索(先読み)も実装しておきましょう。
当然ですが、探索中には末端局面の勝敗情報を得ることはできません。
探索方法は、やはりAlphaGoと同様、「MCTS (Monte Carlo Tree Search: モンテカルロ木探索)」を採用します。MCTSは雑に説明すると、予想確率分布と評価値から繰り返し先読みと評価を行い、探訪数が一番多い(=最も有力な)手を選択する探索手法です。
def search_branch(self, fbg, node_id):
# select and evaluate branch
nd = self.node[node_id]
nd_rate = 0.0 if nd.total_visit == 0 else nd.total_value / nd.total_visit
# calculate action values of all branches at once
with np.errstate(divide='ignore', invalid='ignore'):
rate = nd.value_win / nd.visit_cnt # including dividing by 0
rate[~np.isfinite(rate)] = nd_rate # convert nan, inf to nd_rate
bonus = Tree.cp * nd.prob * sqrt(nd.total_visit) / (nd.visit_cnt + 1)
action_value = rate + bonus
best = np.argmax(action_value)
next_id = nd.next_id[best] # -1 if not expanded
# advance the game
continue_game = fbg.play(nd.cand[best])
# whether nd is leaf node or not
leaf_node = not self.has_next(node_id, best)
leaf_node |= nd.visit_cnt[best] < EXPAND_THRESHOLD
leaf_node |= not continue_game
if leaf_node:
if nd.evaluated[best]:
value = nd.value[best]
else:
prob_, value_ = self.evaluate(fbg)
self.eval_cnt += 1
# flip value because it is opponent's value
value = -value_[0]
nd.value[best] = value
nd.evaluated[best] = True
if continue_game:
if self.node_cnt > 0.85 * NODE_NB:
self.delete_node()
# expand node
next_id = self.create_node(fbg, prob_[0])
next_nd = self.node[next_id]
nd.next_id[best] = next_id
nd.next_hash[best] = fbg.hash()
# copy value_win and visit_cnt
next_nd.total_value -= nd.value_win[best] + value
next_nd.total_visit += nd.visit_cnt[best] + 1
else:
value = -self.search_branch(fbg, next_id)
# backup
nd.total_value += value
nd.total_visit += 1
nd.value_win[best] += value
nd.visit_cnt[best] += 1
return value
学習 と 正答率の推移
このネットワークで繰り返し自己対戦を行い、100対局ごとに探索情報と勝敗から学習していきます。
policyは探索回数の分布とのクロスエントロピーを、valueは勝敗結果との平均二乗誤差を目的関数とします。
lr = tf.placeholder(tf.float32, shape=[], name="learning_rate")
# optimizer and network definition
opt = tf.train.MomentumOptimizer(lr, 0.9)
dn = DualNetwork()
# compute and apply gradients
tower_grads = []
with tf.variable_scope(tf.get_variable_scope()):
for gpu_idx in range(gpu_cnt):
with tf.device("/%s:%d" % (device_name, gpu_idx)):
tf.get_variable_scope().reuse_variables()
policy_, value_ = dn.model(
f_list[gpu_idx], temp=1.0, is_train=True)
policy_ = tf.clip_by_value(policy_, 1e-6, 1)
loss_p = -tf.reduce_mean(tf.reduce_sum(tf.multiply(
p_list[gpu_idx], tf.log(policy_)), 1))
loss_v = tf.reduce_mean(
tf.square(tf.subtract(value_, r_list[gpu_idx])))
if gpu_idx == 0:
vars_train = tf.get_collection("vars_train")
loss_l2 = tf.add_n([tf.nn.l2_loss(v) for v in vars_train])
loss = loss_p + loss_v + 1e-4 * loss_l2
tower_grads.append(opt.compute_gradients(loss))
train_op = opt.apply_gradients(average_gradients(tower_grads))
準備ができたので早速学習を実行させてみましょう。
一応GPUも使えますが、ネットワークがとても軽いためCPUでも速度は変わりません。
$ python fizzbuzzzero.py --learn
0 total games / next epoch: 1
100/100 games
match: accuracy=25.9[%] average length=0.3
train: accuracy=29.0[%] mse=0.500
100 total games / next epoch: 2
100/100 games
match: accuracy=23.1[%] average length=0.3
train: accuracy=24.3[%] mse=0.499
200 total games / next epoch: 3
(...)
100/100 games
match: accuracy=100.0[%] average length=100.0
train: accuracy=96.2[%] mse=0.172
1900 total games / next epoch: 20
100/100 games
match: accuracy=100.0[%] average length=100.0
accuracy seems to be stable at 100%
どうやら収束したようです。最初は0.3だった平均手数(average length)が100になっていますね。
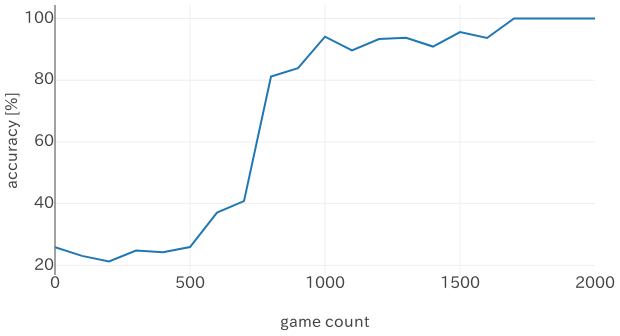
下のグラフが対局数ごとの正答率の推移です。
順調に上昇し、2000対局ほどで100%になりました。時間にすると10分弱です。
最後に、学習したネットワークに実際に出力させてみましょう。(間違えると "[ ]" が付きます。)
1, 2, Fizz, 4, Buzz, Fizz, 7, 8, Fizz, Buzz,
11, Fizz, 13, 14, FizzBuzz, 16, 17, Fizz, 19, Buzz,
Fizz, 22, 23, Fizz, Buzz, 26, Fizz, 28, 29, FizzBuzz,
31, 32, Fizz, 34, Buzz, Fizz, 37, 38, Fizz, Buzz,
41, Fizz, 43, 44, FizzBuzz, 46, 47, Fizz, 49, Buzz,
Fizz, 52, 53, Fizz, Buzz, 56, Fizz, 58, 59, FizzBuzz,
61, 62, Fizz, 64, Buzz, Fizz, 67, 68, Fizz, Buzz,
71, Fizz, 73, 74, FizzBuzz, 76, 77, Fizz, 79, Buzz,
Fizz, 82, 83, Fizz, Buzz, 86, Fizz, 88, 89, FizzBuzz,
91, 92, Fizz, 94, Buzz, Fizz, 97, 98, Fizz, Buzz
全て正解です。完璧にFizzBuzz問題の要求を満たしています。
知識ゼロの状態から、わずか10分でFizzBuzzをマスターできました。
まとめ
人間の知識を用いず、ゼロからの強化学習でFizzBuzzを学習するネットワークを作りました。
すべてのコードはGitHubにアップロードされています。不具合等があればお知らせください。
Twitter(@ymg_aq)もやっていますので、良ければフォローをお願いします。
余談ですが、世の中にはAlpha Zeroで技術的失業した人もいるようです。
あなたがFizzBuzzが書けるからといって、もはや安泰とは言えないかもしれません。
(おまけ)
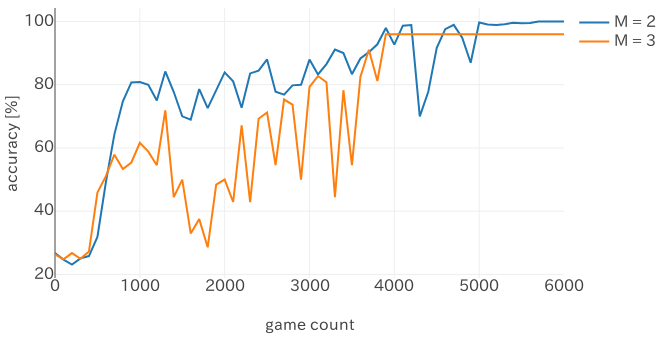
公開しているコードでは --initial_life M でM >= 2(間違いが1回以上許容される)の場合でも学習できます。
Mが大きくなると、わざと間違えて相手を混乱させる戦略を学習するかなと予想したのですが (推移の挙動が怪しいところはそうかもしれません)、最終的には普通に学習しているようです。
しかしM = 3(どちらかが3回間違えると負け) では正答率が100%になっていませんが、どうしてでしょう?出力を見てみましょう。
1, 2, [Buzz], [Buzz], Buzz, Fizz, [Fizz], [Buzz], Fizz, Buzz,
11, Fizz, 13, 14, FizzBuzz, 16, 17, Fizz, 19, Buzz,
Fizz, 22, 23, Fizz, Buzz, 26, Fizz, 28, 29, FizzBuzz,
31, 32, Fizz, 34, Buzz, Fizz, 37, 38, Fizz, Buzz,
41, Fizz, 43, 44, FizzBuzz, 46, 47, Fizz, 49, Buzz,
Fizz, 52, 53, Fizz, Buzz, 56, Fizz, 58, 59, FizzBuzz,
61, 62, Fizz, 64, Buzz, Fizz, 67, 68, Fizz, Buzz,
71, Fizz, 73, 74, FizzBuzz, 76, 77, Fizz, 79, Buzz,
Fizz, 82, 83, Fizz, Buzz, 86, Fizz, 88, 89, FizzBuzz,
91, 92, Fizz, 94, Buzz, Fizz, 97, 98, Fizz, Buzz
…………。
まあ、人間もAIも追い込まれると強いということですね。