量子機械学習 PennyLane と TensorFlow で IRISデータ分類をカスタムループで学習する方法

はじめに

PanneyLaneを持ちいて、量子コンピューティングと TensorFlow の古典コンピューティングを組み合わせたハイブリッドニューラルネットワークを構築するための、やや原始的な方法を紹介します。量子コンピューティングは、従来とは異なる原理で動作し、量子機械学習は、新しいパラダイムを利用して既存の問題を解決してくれると期待しています。しかし、現状の量子回路では十分なデータ量を扱えないことも多く、古典の力も上手に使うことが必要だと思います。

この記事では、量子機械学習の基礎を紹介し、具体的な例としてIRISデータセットの分類問題を取りあげて、速度はイマイチですが、カスタムで動くものを紹介したいと思います。

PennyLane だけを用いた例は下記に記事を書いてますので、ここでは TensorFlow と PennyLane を繋げるところをメインに紹介できればと思います。

古典機械学習の説明は、この記事では割愛してますので、必要な方は、

など参考にしてください。

量子機械学習におけるカスタムトレーニングの重要性

この記事では、カスタムトレーニングの例を紹介しています。はじめにその理由を簡単に紹介します。

カスタムトレーニングの使用は、今の技術的な制約を回避するための一時的な対処療法です。今後の発展により問題は解消されると期待しますが、それまでは、このような手法を用いてとにかく動かすことはできる、という例になります。

バッチ処理とは

機械学習において、一般的な訓練手法の一つにバッチ処理があります。これは、データセットを小さな「バッチ」と呼ばれるサブセットに分割し、それぞれのバッチでモデルを訓練する方法です。TensorFlowのmodel.fitメソッドは、このバッチ処理を簡単に行うための機能を提供します。

量子機械学習における課題

しかし、量子機械学習では特有の課題が存在します。特に、PennyLaneを用いた量子回路は、現在のところTensorFlowのバッチ処理と完全に互換性があるわけではありません。これは、量子回路が一度に1つのサンプルしか処理できないため、バッチ処理を直接行うことが難しいためです。

カスタムトレーニングループの導入

この問題を解決するために、我々はカスタムトレーニングループを導入しました。具体的には、model.fitメソッドを使用せずに、Pythonのforループを用いて各エポックごとにデータセットの全てのサンプルを繰り返し処理します。このアプローチにより、量子機械学習モデルの訓練を効率的ではないにせよ、とにかく確実に動く状態までは持っていけると思います。

プログラムの説明

この記事は、pennylane-0.33.1 を2023.11.17に用いて書いた記事です。

Installing collected packages: semantic-version, rustworkx, autoray, pennylane-lightning, pennylane
Successfully installed autoray-0.6.7 pennylane-0.33.1 pennylane-lightning-0.33.1 rustworkx-0.13.2 semantic-version-2.10.0

コードの全文紹介

まずは、コードの全文を紹介します。

google colab 上で動作された例は下記を参照ください。

PennyLane_TensorFlow_IRIS.ipynb

import tensorflow as tf
import pennylane as qml
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import numpy as np
import matplotlib.pyplot as plt

# IRISデータセットをロード
iris = datasets.load_iris()
X = iris.data  # 特徴量
y = iris.target  # ラベル

# ラベルをone-hotエンコーディング
encoder = OneHotEncoder(sparse_output=False)
y_onehot = encoder.fit_transform(y.reshape(-1, 1))

# データセットを訓練用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y_onehot, test_size=0.3, random_state=42)

# TensorFlowの警告を無視する設定
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)

# 量子デバイスの設定
dev = qml.device("default.qubit", wires=4)

# 量子層の定義
@qml.qnode(dev, interface="tf")
def quantum_layer(inputs, weights):
    # アンプリチュード埋め込みで量子状態を初期化
    qml.templates.AmplitudeEmbedding(inputs, wires=range(4), normalize=True, pad_with=0.0)
    # 強結合量子層を適用
    qml.templates.StronglyEntanglingLayers(weights, wires=range(4))
    # 各量子ビットのZ方向の期待値を出力
    return [qml.expval(qml.PauliZ(i)) for i in range(4)]

# 量子層の重みを初期化
weights = tf.Variable(tf.random.normal([3, 4, 3]))

# 量子モデルの定義
def quantum_model(sample, weights):
    # テンソルから余分な次元を削除
    sample_squeezed = tf.squeeze(sample)
    # 特徴量をパディングして4次元に拡張
    padded_sample = tf.pad(sample_squeezed, tf.constant([[0, 4-len(sample_squeezed)]]), constant_values=0)
    return quantum_layer(padded_sample, weights)

# ニューラルネットワークモデルの構築
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(4, activation="relu"),
    tf.keras.layers.Dense(3, activation="softmax")
])

# モデルのコンパイル
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
# 入力形状を指定してモデルをビルド
model.build(input_shape=(None, 4))

# 最適化器と損失関数の設定
optimizer = tf.keras.optimizers.Adam()
loss_function = tf.keras.losses.CategoricalCrossentropy()

# 訓練データのサンプル数
num_samples = len(X_train)
train_losses = []
val_losses = []
train_accuracies = []
val_accuracies = []

# 訓練ループ
num_epoch = 100
for epoch in range(num_epoch):
    total_loss = 0
    total_accuracy = 0
    for i in range(num_samples):
        with tf.GradientTape() as tape:
            # 訓練データのサンプルをテンソルに変換
            sample = tf.expand_dims(tf.convert_to_tensor(X_train[i], dtype=tf.float32), axis=0)
            label = tf.expand_dims(tf.convert_to_tensor(y_train[i], dtype=tf.float32), axis=0)

            # 古典層からの出力を取得
            classical_output = model.layers[0](sample)
            # 量子層からの出力を取得
            quantum_output = quantum_model(classical_output, weights)
            # 出力層に渡すための次元追加
            quantum_output_expanded = tf.expand_dims(quantum_output, axis=0)
            # 出力層からの予測値を取得
            predictions = model.layers[-1](quantum_output_expanded)
            # 損失と精度を計算
            loss = loss_function(label, predictions)
            accuracy = tf.keras.metrics.categorical_accuracy(label, predictions)

            # 勾配を計算し、重みを更新
            gradients = tape.gradient(loss, model.trainable_variables + [weights])
            optimizer.apply_gradients(zip(gradients, model.trainable_variables + [weights]))
            # 損失と精度を加算
            total_loss += loss.numpy()
            total_accuracy += tf.reduce_mean(accuracy).numpy()

    # 平均損失と精度を計算
    avg_loss = total_loss / num_samples
    avg_accuracy = total_accuracy / num_samples
    train_losses.append(avg_loss)
    train_accuracies.append(avg_accuracy)

    # 検証データでの損失と精度を計算
    val_loss = 0
    val_accuracy = 0
    num_val_samples = len(X_test)
    for i in range(num_val_samples):
        # 検証データのサンプルをテンソルに変換
        sample = tf.expand_dims(tf.convert_to_tensor(X_test[i], dtype=tf.float32), axis=0)
        label = tf.expand_dims(tf.convert_to_tensor(y_test[i], dtype=tf.float32), axis=0)

        # 古典層と量子層からの出力を取得
        classical_output = model.layers[0](sample)
        quantum_output = quantum_model(classical_output, weights)
        quantum_output_expanded = tf.expand_dims(quantum_output, axis=0)
        predictions = model.layers[-1](quantum_output_expanded)
        # 損失と精度を計算
        loss = loss_function(label, predictions)
        accuracy = tf.keras.metrics.categorical_accuracy(label, predictions)

        # 損失と精度を加算
        val_loss += loss.numpy()
        val_accuracy += tf.reduce_mean(accuracy).numpy()

    # 平均損失と精度を計算
    avg_val_loss = val_loss / num_val_samples
    avg_val_accuracy = val_accuracy / num_val_samples
    val_losses.append(avg_val_loss)
    val_accuracies.append(avg_val_accuracy)

    # 各エポックの結果を表示
    print(f"Epoch {epoch + 1}: Train Loss = {avg_loss}, Train Accuracy = {avg_accuracy}, "
          f"Val Loss = {avg_val_loss}, Val Accuracy = {avg_val_accuracy}")

# 訓練と検証の損失と精度のグラフを表示
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(train_losses, label='Train Loss')
plt.plot(val_losses, label='Val Loss')
plt.title('Training and Validation Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(train_accuracies, label='Train Accuracy')
plt.plot(val_accuracies, label='Val Accuracy')
plt.title('Training and Validation Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
plt.savefig("pennylane_tensorflow_iris.png")
plt.show()

コードの詳細な説明

データの前処理

IRISデータセットは、アヤメの花に関するデータセットです。scikit-learnからデータセットを読み込み、特徴量とラベルを取得しています。

ラベルはone-hotエンコーディングを行い、データセットを訓練用とテスト用に分割します。

encoder = OneHotEncoder(sparse_output=False)
y_onehot = encoder.fit_transform(y.reshape(-1, 1))
X_train, X_test, y_train, y_test = train_test_split(X, y_onehot, test_size=0.3, random_state=42)

量子デバイスの設定

PennyLaneを使って、量子デバイス（量子ビットの集合）を初期化します。
wires は 4 にしていますが、ここは問題に応じて変更します。

dev = qml.device("default.qubit", wires=4)

量子層の構築

量子層は、AmplitudeEmbeddingと強結合量子層を含みます。強結合量子層は強く結合された量子層を量子ビットに適用し、このレイヤーにより、量子ビット間の結合が強化され、量子状態の複雑さを高めるのに役立ちます。

@qml.qnode(dev, interface="tf")
def quantum_layer(inputs, weights):
    qml.templates.AmplitudeEmbedding(inputs, wires=range(4), normalize=True, pad_with=0.0)
    qml.templates.StronglyEntanglingLayers(weights, wires=range(4))
    return [qml.expval(qml.PauliZ(i)) for i in range(4)]

4つの量子ビット上で動作し、各量子ビットからの期待値を出力として返します。

量子モデルの定義

# 量子モデルの定義
def quantum_model(sample, weights):
    # テンソルから余分な次元を削除
    sample_squeezed = tf.squeeze(sample)
    # 特徴量をパディングして4次元に拡張
    padded_sample = tf.pad(sample_squeezed, tf.constant([[0, 4-len(sample_squeezed)]]), constant_values=0)
    return quantum_layer(padded_sample, weights)

• tf.squeeze は TensorFlow で提供される関数で、テンソルからサイズが1の次元を削除します。たとえば、形状が (1, n) または (n, 1) のテンソルがあるとき、tf.squeeze を使うと形状が (n,) になります。入力データが量子回路で必要とされる一次元のデータ形状になります。

• tf.pad(sample_squeezed, tf.constant([[0, 4-len(sample_squeezed)]]), constant_values=0) は、sample_squeezed テンソルをパディング（埋める）して4次元に拡張します。量子層では、量子ビットの数に応じて特定の次元の入力が必要（この場合は4量子ビット）なので、他の問題の拡張用に用意しています。この例では４次元の入力で、４量子ビットなので、なくても大丈夫です。

このステップで入力データを量子回路が処理できる形式に変換し、古典的なニューラルネットワークの出力を量子層に適切に統合ためのバッファーの働きをしています。

ニューラルネットワークモデルの構築

TensorFlowを使用して古典的なニューラルネットワーク層を構築し、最終層にはソフトマックス活性化関数を適用します。

model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(4, activation="relu"),
    tf.keras.layers.Dense(3, activation="softmax")
])

訓練前の重みの初期化

訓練の開始前に、

model.build(input_shape=(None, 4))

を持ちいて、重みを初期化します。今回のように、カスタムトレーニングループを使用するとき（model.fit()を使用せずに手動でトレーニングループを書いている場合）、重みが初期化されていないため、訓練前に model.build() が必要です。

訓練ループ

各エポックごとに、訓練データの各サンプルに対して以下の手順を実行します。

1. サンプルをテンソルに変換。
2. 古典層からの出力を取得。
3. 量子モデルを適用して量子層の出力を取得。
4. 損失と精度を計算し、重みを更新。

また、検証データに対しても同様の手順を実行し、損失と精度を計算します。tf.keras.metrics.categorical_accuracy は、分類問題におけるモデルの正答率（精度）を計算してくれます。100個のデータポイントのうち、モデルが90個を正しく分類した場合、正答率は90%という感じです。

検証データについて補足すると、val_loss, val_accuracy = model.evaluate(X_test, y_test, verbose=0) のように、通常の古典機械学習であれば model.evaluate()メソッドがよいのですが、今回は古典的なニューラルネットワークモデルのみを使用しており、量子層（quantum_model）を含んでいないため、正確な評価ができません。そのため、訓練ループと同様の方法で量子層を組み込んだ評価処理を行なっています。

訓練ループ内の tf.GradientTape の役割

with tf.GradientTape() as tape: という構文は TensorFlow で勾配を計算する際に使用され、特に自動微分を行う際に重要です。この構文の理由と重要性は下記になります。

• コンテキストマネージャとしての機能:
  • with 文は Python のコンテキストマネージャです。コンテキストマネージャは、特定のブロックの実行前後にセットアップやクリーンアップのためのコードを自動的に実行します。
  • with ブロック内で行われた操作（この場合はモデルの計算）について、GradientTape() は必要な情報（例えばテンソルの演算履歴）を記録します。
• 自動微分のための記録:
  • tf.GradientTape() は TensorFlow が提供する自動微分機能の一部です。この機能は、与えられた計算に関連する勾配を効率的に計算します。
  • with tf.GradientTape() as tape: ブロック内で行われる計算は全て「記録」され、後でこれらの計算に基づいて勾配が計算されます。
• リソースの管理:
  • GradientTape は計算リソースを消費します。特に、複雑なモデルや大規模なデータに対する計算では、多くの情報が記録されるため、メモリ使用量が増加します。
  • with ブロックを抜けると、GradientTape によって使用されたリソースは自動的に解放されます。これにより、メモリリークのリスクを減らし、プログラムの効率を高めることができます。

つまり、with tf.GradientTape() as tape: は TensorFlow で微分計算を行う際に、必要な計算を効率的かつ安全に記録し、リソースを適切に管理します。これにより、機械学習モデルのトレーニング中の勾配計算が簡素化され、最適化されます。

訓練ループ内のパラメータの更新

# 勾配を計算し、重みを更新
gradients = tape.gradient(loss, model.trainable_variables + [weights])
optimizer.apply_gradients(zip(gradients, model.trainable_variables + [weights]))

tape.gradient で計算された勾配を使用して、optimizer.apply_gradientsでモデルのパラメータを更新します。

tf.GradientTape() を使用して計算された gradients は、quantum_layer 関数における weights に関する損失関数の勾配です。
optimizer は、モデルの学習率や更新アルゴリズム（この場合は Adam）を定義するオブジェクトです。apply_gradients メソッドは、計算された勾配を使用して、パラメータ（この場合は model.trainable_variables + [weights]）を更新します。
zip(gradients, model.trainable_variables + [weights]) は、各勾配とそれに対応するパラメータを組み合わせるために使用されます。

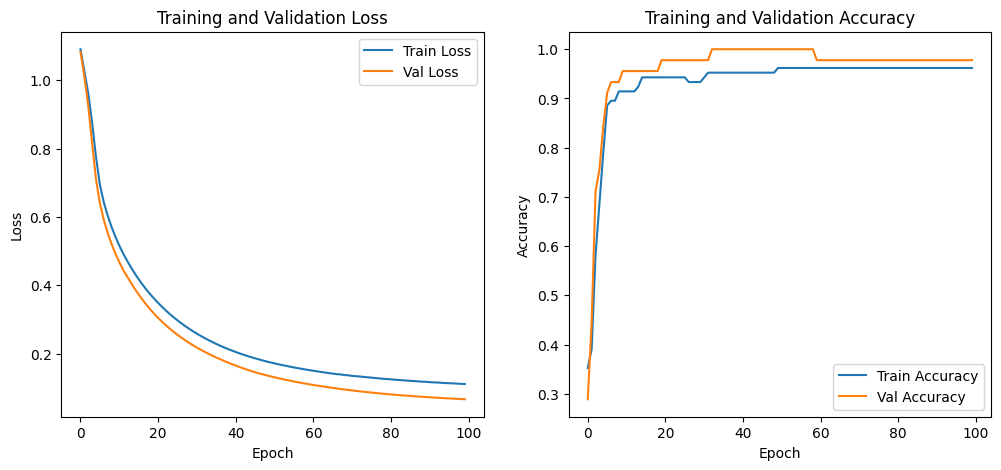
実行結果

google colab で実行した結果

に実行結果を紹介しています。

Epoch 1: Train Loss = 1.0901739739236378, Train Accuracy = 0.3523809523809524, Val Loss = 1.0822558919588725, Val Accuracy = 0.28888888888888886
Epoch 2: Train Loss = 1.0260852416356405, Train Accuracy = 0.3904761904761905, Val Loss = 1.009931124581231, Val Accuracy = 0.4444444444444444
...
Epoch 99: Train Loss = 0.1123230253390613, Train Accuracy = 0.9619047619047619, Val Loss = 0.06787581963257658, Val Accuracy = 0.9777777777777777
Epoch 100: Train Loss = 0.11178601591714792, Train Accuracy = 0.9619047619047619, Val Loss = 0.06731935979591476, Val Accuracy = 0.9777777777777777

となり、学習は進んでいるようです。

1 Epoch が 1分弱くらいでしょうか、、ちょっと遅い感は否めませんが、、動きはします。(最適化などの良い方法あれば教えてください。。)

トラブルシューティング

よくあるエラーの例

バッチ処理の非対応

AmplitudeEmbedding does not support batched Tensorflow features.

というメッセージは、AmplitudeEmbedding が TensorFlow のバッチ処理された特徴量をサポートしていないためです(2023.11.17現在)。AmplitudeEmbedding は個別のサンプルに対してのみ機能し、バッチ（つまり複数のサンプルの集まり）では動作しません。

この制約を回避するには、データを個々のサンプルとしてモデルに供給する必要があります。これを実現する一般的な方法は、カスタムのトレーニングループを作成することです。この記事では、各エポックで全てのサンプルを繰り返し処理し、それぞれのステップでモデルを更新しています。 GradientTape は TensorFlow で勾配を計算するためのコンテキストマネージャで、各ステップでモデルの予測を生成し、損失を計算してから、勾配を計算してモデルのパラメータを更新しています。

ただし、この方法は計算コストが高くなる可能性に注意が必要です。

古典層と量子層の型の不一致

Input 0 of layer "dense_12" is incompatible with the layer: expected min_ndim=2, found ndim=1. Full shape received: (4,)

などのエラーを見たら、量子と古典の型の不一致の可能性が高いです。

古典層はバッチ処理された2次元入力を期待するのに対し、量子層は単一の1次元サンプルを期待する設計が多いかと思います。この記事の例では、古典的な層が2次元の入力を受け取りつつ、量子層が1次元の入力を受け取ることが可能になるように、両者を分けて、型変換を明示的に行うことにしています。ただし、この方法は一時的な解決策で、将来的には不要になると期待しています。

自動微分の複素数のキャストの warning

WARNING:tensorflow:You are casting an input of type complex128 to an incompatible dtype float32. This will discard the imaginary part and may not be what you intended.

という warning がでることがあります。

この warning は、量子回路では基本的に実数の期待値だけ変換しているにも関わらず、tape.gradient で勾配を計算するときに発生するもので、

でも議論されてますが、原因がよくわからないようなので、無視すればよいです。この例では、

# TensorFlowの警告を無視する設定
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)

を挿入して warning を止めています。

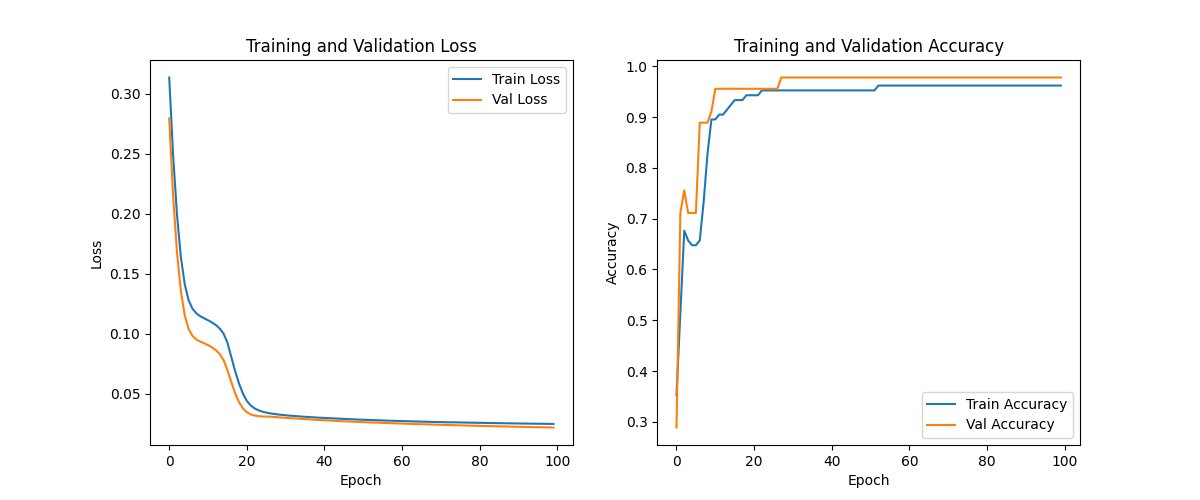
loss function の違い

MeanSquaredError を用いた場合

tf.keras.losses.CategoricalCrossentropy() ではなくて、tf.keras.losses.MeanSquaredError を用いた例も google colab にあげています。

tf.keras.losses.MeanSquaredError を用いたコード全文

import tensorflow as tf
import pennylane as qml
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import numpy as np
import matplotlib.pyplot as plt

# IRISデータセットをロード
iris = datasets.load_iris()
X = iris.data  # 特徴量
y = iris.target  # ラベル

# ラベルをone-hotエンコーディング
encoder = OneHotEncoder(sparse_output=False)
y_onehot = encoder.fit_transform(y.reshape(-1, 1))

# データセットを訓練用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X, y_onehot, test_size=0.3, random_state=42)

# TensorFlowの警告を無視する設定
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)

# 量子デバイスの設定
dev = qml.device("default.qubit", wires=4)

# 量子層の定義
@qml.qnode(dev, interface="tf")
def quantum_layer(inputs, weights):
    qml.templates.AmplitudeEmbedding(inputs, wires=range(4), normalize=True, pad_with=0.0)
    qml.templates.StronglyEntanglingLayers(weights, wires=range(4))
    return [qml.expval(qml.PauliZ(i)) for i in range(4)]

# 量子層の重みを初期化
weights = tf.Variable(tf.random.normal([3, 4, 3]))

# 量子モデルの定義
def quantum_model(sample, weights):
    sample_squeezed = tf.squeeze(sample)
    padded_sample = tf.pad(sample_squeezed, tf.constant([[0, 4-len(sample_squeezed)]]), constant_values=0)
    return quantum_layer(padded_sample, weights)

# ニューラルネットワークモデルの構築
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(4, activation="relu"),
    tf.keras.layers.Dense(3)  # アクティベーション関数を削除
])

# モデルのコンパイル、損失関数を MeanSquaredError に変更
model.compile(optimizer='adam', loss=tf.keras.losses.MeanSquaredError(), metrics=['accuracy'])
model.build(input_shape=(None, 4))

# 最適化器と損失関数の設定
optimizer = tf.keras.optimizers.Adam()
loss_function = tf.keras.losses.MeanSquaredError()

num_samples = len(X_train)
train_losses = []
val_losses = []
train_accuracies = []
val_accuracies = []

# 訓練ループ# 訓練ループ
num_epoch = 100
for epoch in range(num_epoch):
    total_loss = 0
    total_accuracy = 0
    for i in range(num_samples):
        with tf.GradientTape() as tape:
            # 訓練データのサンプルをテンソルに変換
            sample = tf.expand_dims(tf.convert_to_tensor(X_train[i], dtype=tf.float32), axis=0)
            label = tf.expand_dims(tf.convert_to_tensor(y_train[i], dtype=tf.float32), axis=0)

            # 古典層からの出力を取得
            classical_output = model.layers[0](sample)
            # 量子層からの出力を取得
            quantum_output = quantum_model(classical_output, weights)
            # 出力層に渡すための次元追加
            quantum_output_expanded = tf.expand_dims(quantum_output, axis=0)
            # 出力層からの予測値を取得
            predictions = model.layers[-1](quantum_output_expanded)

            # 損失と精度を計算（精度の計算方法を変更）
            loss = loss_function(label, predictions)
            predicted_class = tf.argmax(predictions, axis=1)
            true_class = tf.argmax(label, axis=1)
            accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted_class, true_class), tf.float32))

            # 勾配を計算し、重みを更新
            gradients = tape.gradient(loss, model.trainable_variables + [weights])
            optimizer.apply_gradients(zip(gradients, model.trainable_variables + [weights]))
            # 損失と精度を加算
            total_loss += loss.numpy()
            total_accuracy += tf.reduce_mean(accuracy).numpy()

    # 平均損失と精度を計算
    avg_loss = total_loss / num_samples
    avg_accuracy = total_accuracy / num_samples
    train_losses.append(avg_loss)
    train_accuracies.append(avg_accuracy)

    # 検証データでの損失と精度を計算
    val_loss = 0
    val_accuracy = 0
    num_val_samples = len(X_test)
    for i in range(num_val_samples):
        # 検証データのサンプルをテンソルに変換
        sample = tf.expand_dims(tf.convert_to_tensor(X_test[i], dtype=tf.float32), axis=0)
        label = tf.expand_dims(tf.convert_to_tensor(y_test[i], dtype=tf.float32), axis=0)

        # 古典層と量子層からの出力を取得
        classical_output = model.layers[0](sample)
        quantum_output = quantum_model(classical_output, weights)
        quantum_output_expanded = tf.expand_dims(quantum_output, axis=0)
        predictions = model.layers[-1](quantum_output_expanded)

        # 損失と精度を計算（精度の計算方法を変更）
        loss = loss_function(label, predictions)
        predicted_class = tf.argmax(predictions, axis=1)
        true_class = tf.argmax(label, axis=1)
        accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted_class, true_class), tf.float32))

        # 損失と精度を加算
        val_loss += loss.numpy()
        val_accuracy += tf.reduce_mean(accuracy).numpy()

    # 平均損失と精度を計算
    avg_val_loss = val_loss / num_val_samples
    avg_val_accuracy = val_accuracy / num_val_samples
    val_losses.append(avg_val_loss)
    val_accuracies.append(avg_val_accuracy)

    # 各エポックの結果を表示
    print(f"Epoch {epoch + 1}: Train Loss = {avg_loss}, Train Accuracy = {avg_accuracy}, "
          f"Val Loss = {avg_val_loss}, Val Accuracy = {avg_val_accuracy}")

# 訓練と検証の損失と精度のグラフを表示
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(train_losses, label='Train Loss')
plt.plot(val_losses, label='Val Loss')
plt.title('Training and Validation Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(train_accuracies, label='Train Accuracy')
plt.plot(val_accuracies, label='Val Accuracy')
plt.title('Training and Validation Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
plt.savefig("pennylane_tensorflow_iris.png")
plt.show()

結果の例はこちらです。

最後に

この記事では、量子機械学習 PennyLane と TensorFlow を用いた IRISデータセットの分類をカスタムループで学習する方法を紹介しました。量子コンピューティングは、機械学習の分野に新たな可能性をもたらすと期待してますので、動かしながら想像力を働かせてみるのもよいかな、という感じの記事でした。