2. Pythonで綴る多変量解析 8-2. k近傍法 [ウェイトのかけ方] [回帰モデル]

• k近傍法は、予測に使用される重み関数（ウェイトのかけ方）が２通りあります。
  • uniform : 一様な重みで、近傍のすべての点が等しく重みづけされます。
  • distance : 点を距離の逆数で重みづけします。従って、近い点の方が、遠い点よりも大きな影響力を持ちます。
• デフォルトは uniform なので、distanceとするにはインスタンス生成時に引数で渡してやる必要があります。

これらの違いが、どのように予測結果に影響してくるのでしょうか。
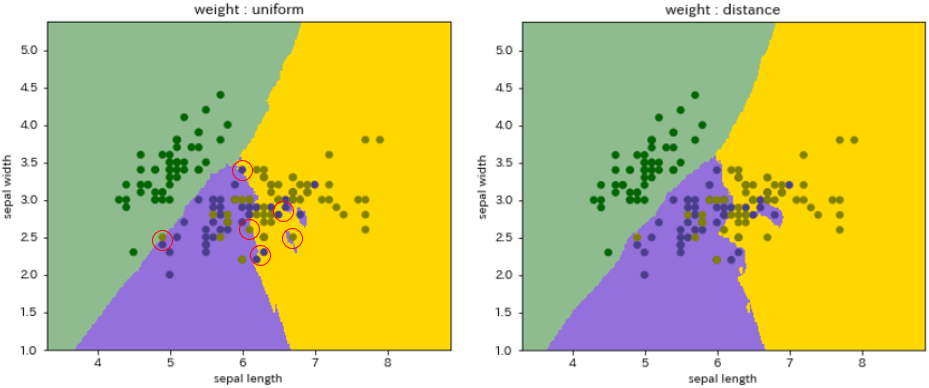
前回の分類モデルのケースを例として示します。

• 境界が微妙に異なりますが、特に赤い○囲みの箇所に明らかな違いが見られます。
• 概してdistanceの方が、よりデータに対して忠実に境界が分けられています。

さらに、回帰モデルのケースで比較してみたいと思います。

⑴ ライブラリのインポート

import numpy as np
import pandas as pd

# scikit-learn系ライブラリ
from sklearn.datasets import load_boston             # ボストン住宅価格のデータセット
from sklearn.model_selection import train_test_split # データ分割ユーティリティ
from sklearn.neighbors import KNeighborsRegressor    # k-NR回帰モデルのメソッド

# 可視化ライブラリ
import matplotlib.pyplot as plt
import seaborn as sns

# matplotlibの日本語表示モジュール
!pip install japanize-matplotlib
import japanize_matplotlib

• k近傍法は、主に分類モデルとしてk-NN（k-Nearest Neighbor）の名で通っていますが、scikit-learnのneighborsモジュールで回帰モデルはKNeighborsRegressorメソッドになります。

1. データを準備する

• scikit-learnのデータセットから「ボストン」を取得します。
• 米マサチューセッツ州北東部にある大都市ボストンの「住宅価格」を目的変数として、犯罪率や一戸当たり平均室数、交通アクセスなど13の属性情報を説明変数とする全506サンプルのデータセットです。

⑵ データの取得と整理

# データセットを取得
boston = load_boston()

# 説明変数をDataFrameに変換
df = pd.DataFrame(boston.data, columns=boston.feature_names)

# 目的変数を連結
df = pd.concat([df, pd.DataFrame(boston.target, columns=['MEDV'])], axis=1)
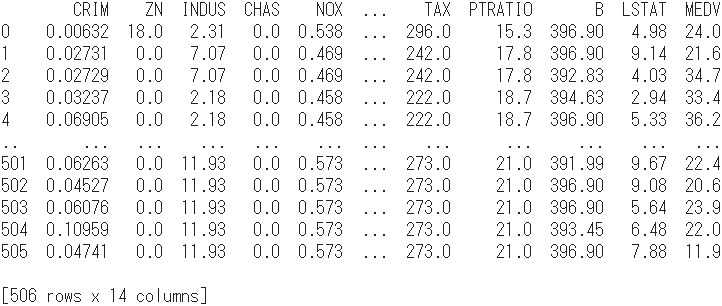
print(df)

• 最右列「MEDV」は median value の略で、「1000ドル台の持家の中央値」と定義される目的変数（住宅価格）に当たります。
• 最左列「CRIM(crime rate)：犯罪率」から「LSTAT(lower status)：下層階級比率」まで、説明変数は全部で13ありますが、話を簡単にするために１変数のみ選び出すことにします。

⑶ 相関行列による分析軸の検討

• 全変数間の相関行列を作成し、住宅価格と相関の高い変数に注目します。

# 相関行列を作成
correlation_matrix = np.corrcoef(df.T)

# 行･列ラベル
names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 
         'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']

# 相関行列をDataFrameに変換
correlation_df = pd.DataFrame(correlation_matrix, columns = names, index = names)

# ヒートマップを描画
plt.figure(figsize=(10,8))
sns.heatmap(correlation_df, annot=True, cmap='coolwarm')

• 相関行列にはNumpyのcorrcoef()関数を使いますが、渡すデータを.Tで行と列を転置することにより変数間の相関を算出させます。
• ヒートマップには seaborn を利用しています。heatmap()の引数annot=Trueは、図中のセル毎に値を表示させます。

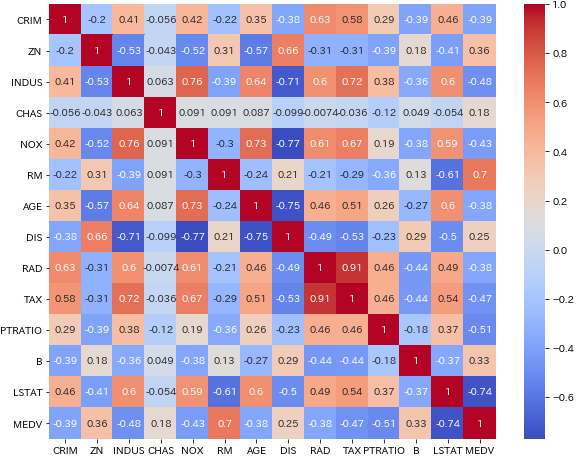
• 住宅価格(MEDV)と強い相関を示す変数としては、「下層階級比率(LSTAT)」が-0.74で強い負の相関を示し、また「一戸当たり平均室数(RM)」が0.70で強い正の相関を示しています。
• たいてい部屋数が多くなれば価格は高くなりますし、低所得層が多い地域であれば相場価格は低いということでしょう。シンプルに「一戸当たりの平均室数(RM)」を採用することにします。

⑷ データの抽出と分割

# 2変数のみ抽出
df_extraction = df[['RM', 'MEDV']]

# 変数X, yを設定
X = np.array(df_extraction['RM'])
y = np.array(df_extraction['MEDV'])

X = X.reshape(len(X), 1) # 2次元に変換
y = y.reshape(len(y), 1)

# 訓練･テストにデータ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0)

X_train = X_train.reshape(len(X_train), 1) # 2次元に変換
X_test = X_test.reshape(len(X_test), 1)
y_train = y_train.reshape(len(y_train), 1)
y_test = y_test.reshape(len(y_test), 1)

• 説明変数RMと目的変数MEDVのみを抽出し、それぞれ変数Xとyとして訓練用・テスト用に分割します。

2. kパラメータの検討

⑸ kパラメータを変更しながらk-NRを実行

• kを1～20個まで変更しながらk-NRを実行し、訓練データとテストデータの正解率の変化を観察します。

# 正解率を格納する変数
train_accuracy = []
test_accuracy = []

for k in range(1,21):
    kNR = KNeighborsRegressor(n_neighbors = k) # インスタンス生成
    kNR.fit(X_train, y_train) # 学習
    train_accuracy.append(kNR.score(X_train, y_train)) # 訓練の正解率
    test_accuracy.append(kNR.score(X_test, y_test)) # テストの正解率

# 正解率をarrayに変換
training_accuracy = np.array(train_accuracy)
test_accuracy = np.array(test_accuracy)

⑹ 最適なkパラメータを選択

• 訓練とテストの正解率の変化を可視化し、併せて正解率の差分をグラフに示します。

# 訓練・テストの正解率の推移
plt.figure(figsize=(6, 4))

plt.plot(range(1,21), train_accuracy, label='訓練')
plt.plot(range(1,21), test_accuracy, label='テスト')

plt.xticks(np.arange(0, 21, 1)) # x軸目盛
plt.xlabel('k個数')
plt.ylabel('正解率')
plt.title('正解率の推移')

plt.grid()
plt.legend()

# 正解率の差分の推移
plt.figure(figsize=(6, 4))

difference = np.abs(train_accuracy - test_accuracy) # 差分を計算
plt.plot(range(1,21), difference, label='差分')

plt.xticks(np.arange(0, 21, 1)) # x軸目盛
plt.xlabel('k個数')
plt.ylabel('差分(train - test)')
plt.title('正解率の差分の推移')

plt.grid()
plt.legend()

plt.show()

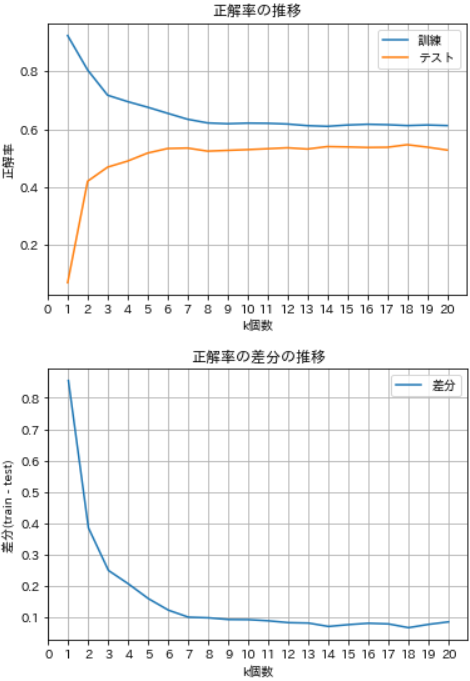
• kが増えるにつれて訓練の正解率は減少し、逆にテストの方は増加していますが、どちらもk=9くらいからほぼ横ばいとなっています。
• 差分をみると、順次k=14までは減少傾向にあることから、k=14を採用することにします。

3. モデルの実行と評価

• 予測に用いるダミーデータを作成します。

⑺ ダミーデータを作成

# 等差数列を生成
t = np.linspace(1, 10, 1000) # 開始値, 終了値, 要素数

# 2次元に形状を変換
T = t.reshape(1000, 1)

⑻ 回帰モデルの実行と可視化

n_neighbors = 14

plt.figure(figsize=(12,5))

for i, w in enumerate(['uniform', 'distance']):
    model = KNeighborsRegressor(n_neighbors, weights=w)
    model = model.fit(X, y)
    y_ = model.predict(T)

    plt.subplot(1, 2, i + 1)
    plt.scatter(X, y, color='limegreen', label='データ')
    plt.plot(T, y_, color='navy', lw=1, label='予測値')
    plt.legend()
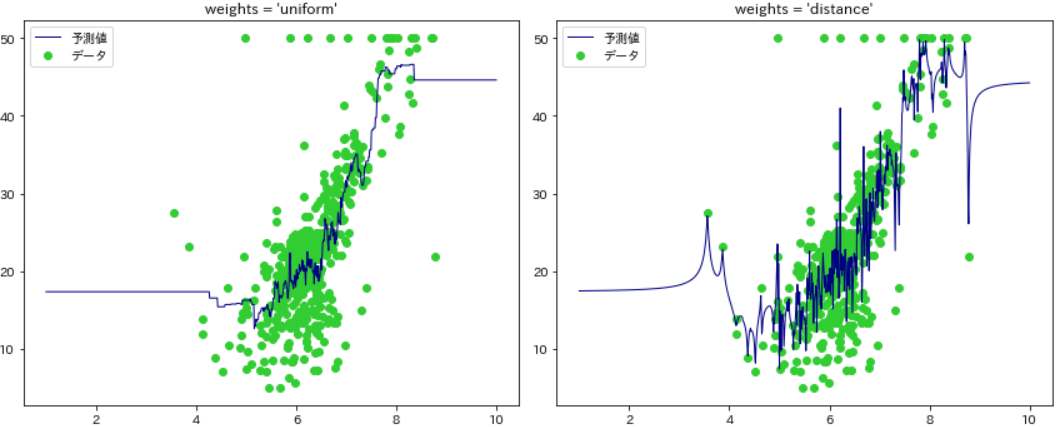
    plt.title("weights = '%s'" % (w))

plt.tight_layout()
plt.show()

• tight_layout()は、サブプロットのパラメータ（軸目盛、軸ラベル、タイトルの範囲）を自動的に調整して、サブプロットがグラフの領域内にぴったりと収まるようにしてくれます。

• まず一見してわかるのが、distanceの方は予測値の変動が著しく、データにオーバーフィッティング（過学習）しています。
• これに対して uniform の方は情報の要約ができており、デフォルトが uniform だというのも頷ける結果となりました。