- いくつかのグループがあり、それらに属するサンプル群の属性はわかっていて、そこへ別の新たなサンプルが加わったとき、どのグループに属するかを求めるのが **k-NN(k-Nearest Neighbor : k近傍法)**です。
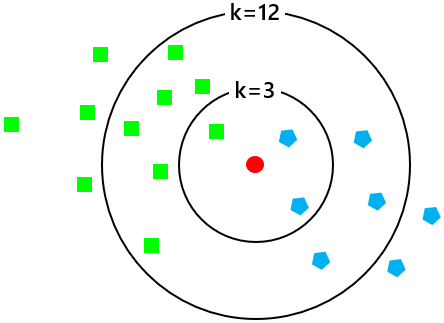
- 具体的には、既存のサンプル群から、新たなサンプルと属性が近い K 個を取得し、それらの中で多数派のグループに決定するという分類方法です。この k 個がk-NNと呼ばれる所以です。
- かりにk=3とすると青グループと判断され、またk=12とすると緑グループに分類されるので、k の個数によって判断は違ったものになります。
回帰にも使えますが、ここでは分類のケースを行ないます。
⑴ ライブラリのインポート
import numpy as np
import pandas as pd
from sklearn import datasets
# sklearn.neighborsモジュールのk-NNメソッド
from sklearn.neighbors import KNeighborsClassifier
# sklearnのデータ分割ユーティリティ
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# カラーマップを生成するメソッド
from matplotlib.colors import ListedColormap
# matplotlibの日本語表示モジュール
!pip install japanize-matplotlib
import japanize_matplotlib
データを準備する
- scikit-learnのデータセットから「アイリス」を取得します。
- 花菖蒲の「花びら」と「がく」の長さ・幅を計測した4つの特徴量があり、3種類×各50からなる全150サンプルのデータです。この3種類がグループに相当します。
| 変数名 | 意味 | 注記 | データ型 | |
|---|---|---|---|---|
| 0 | species | 種類 | Setosa=0, Versicolour=1, Virginica=2 | int64 |
| 1 | sepal length | がく片の長さ | 連続量(cm) | float64 |
| 2 | sepal width | がく片の幅 | 連続量(cm) | float64 |
| 3 | petal length | 花びらの長さ | 連連続量(cm) | float64 |
| 4 | petal width | 花びらの幅 | 連続量(cm) | float64 |
⑵ データの取得
iris = datasets.load_iris()
- データの内容を、説明変数(特徴量)と目的変数(種類)のそれぞれについて確認しておきます。
# 説明変数(特徴量)
print("ラベル:\n", iris.feature_names)
print("形状:\n", iris.data.shape)
print("先頭10行:\n", iris.data[0:10, :])
# 目的変数(種類)
print("ラベル:\n", iris.target_names)
print("形状:\n", iris.target.shape)
print("全表示:\n", iris.target)
⑶ データの分割
X_train, X_test, y_train, y_test = train_test_split(
iris.data,
iris.target,
stratify = iris.target, # 層化サンプリング
random_state = 0)
- 引数の
stratify = iris.targetで、種類(iris.target)による層化サンプリングを指定しています。デフォルトですとランダムサンプリングになりますので、ここでは特に訓練用・テスト用ともに3種類の構成比を保持するように分割します。 - 訓練用の目的変数だけ内容を確認しておきましょう。
print("形状:", y_train.shape)
# ユニークな要素ごとの個数を取得
np.unique(y_train, return_counts=True)
- デフォルトで訓練用として75%が割り当てられ、その112サンプルの中身は3種類で均等配分されています。
k の個数を決定する
⑷ kパラメータを変更しながらk-NNを実行
- kを3~20個まで変更しながらk-NNを実行し、訓練データとテストデータの正解率の変化を観察します。
# 正解率を格納する変数
training_accuracy = []
test_accuracy = []
# kを変更しながらk-NNを実行し、正解率を取得
for k in range(3,21):
# kを渡してインスタンスを生成し、データをfitさせてモデルを生成
kNN = KNeighborsClassifier(n_neighbors = k)
kNN.fit(X_train, y_train)
# scoreで正解率を取得し、順次格納
training_accuracy.append(kNN.score(X_train, y_train))
test_accuracy.append(kNN.score(X_test, y_test))
# 正解率をnumpyの配列に変換
training_accuracy = np.array(training_accuracy)
test_accuracy = np.array(test_accuracy)
⑸ 最適なkパラメータを選択
- 訓練データとテストデータの正解率の変化を可視化し、併せて正解率の差分をグラフに示します。
# 訓練用・テスト用の正解率の推移
plt.figure(figsize=(6, 4))
plt.plot(range(3,21), training_accuracy, label='訓練')
plt.plot(range(3,21), test_accuracy, label='テスト')
plt.xticks(np.arange(2, 21, 1)) # x軸目盛
plt.xlabel('k個数')
plt.ylabel('正解率')
plt.title('正解率の推移')
plt.grid()
plt.legend()
# 正解率の差分の推移
plt.figure(figsize=(6, 4))
difference = np.abs(training_accuracy - test_accuracy) # 差分を計算
plt.plot(range(3,21), difference, label='差分')
plt.xticks(np.arange(2, 21, 1)) # x軸目盛
plt.xlabel('k個数')
plt.ylabel('差分(train - test)')
plt.title('正解率の差分の推移')
plt.grid()
plt.legend()
plt.show()
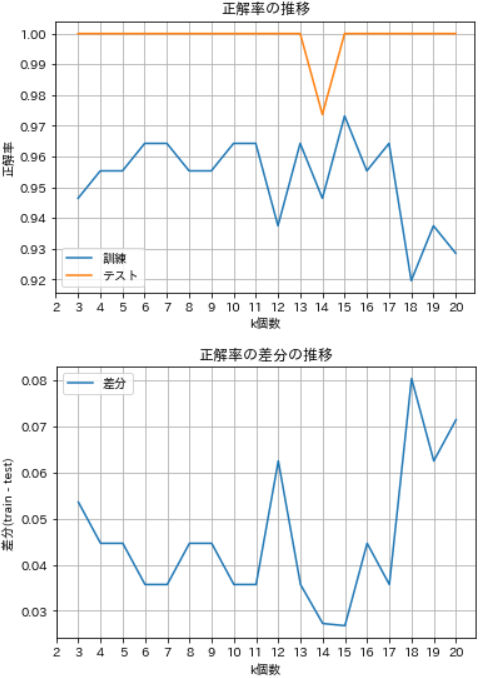
- kを3~20個まで変化させてみたところ、まずテストでは、k=14で落ち込むほかは100%で一定しています。
- 一方、訓練では、k=3~6にかけて漸増傾向を示し、以降k=11までは横ばいぎみとなり、k=12で落ち込みますが以降は高下しながら増加傾向を示し、k=15を頂点として減少に転じています。
- また、正解率の差分の推移を見ると、k=15で訓練とテストの正解率が最も近くなることがわかります。
k-NNを実行し可視化する
⑹ 最適なkパラメータでk-NNを再実行
- k=15を採用し、改めてk-NNを実行します。
- ここでは、4つの特徴量のうち先頭2つだけを使用することとします。
# kの個数を指定
k = 15
# 説明変数Xと目的変数yを設定
X = iris.data[:, :2]
y = iris.target
# インスタンスを作成し、データをフィットさせてモデルを生成
model = KNeighborsClassifier(n_neighbors=k)
model.fit(X, y)
⑺ コンター図(等値線図)にプロット
- 2次元平面上に各グループの境界を描くため、メッシュ状のデータ
Zを作成します。
# メッシュ間隔を指定
h = 0.02
# カラーマップを作成
cmap_surface = ListedColormap(['darkseagreen', 'mediumpurple', 'gold']) # 面グラフ用
cmap_dot = ListedColormap(['darkgreen', 'darkslateblue', 'olive']) # 散布図用
# x,y軸の最小値・最大値を取得
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
# 指定のメッシュ間隔で格子列を生成
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# 格子列をモデルに渡して予測
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape) # 形状変換
-
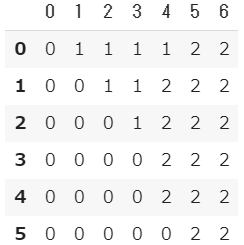
xxとyyの格子列データをravel()関数で一次元に平坦化し、numpyのc_()関数で結合したものをモデルに渡して予測させます。 - 例として、メッシュ間隔を 0.8 に拡大した場合の Z を示します。
- このように Z は、指定した間隔でメッシュ状になったセル毎に種類(グループ)の情報を持つデータになっています。
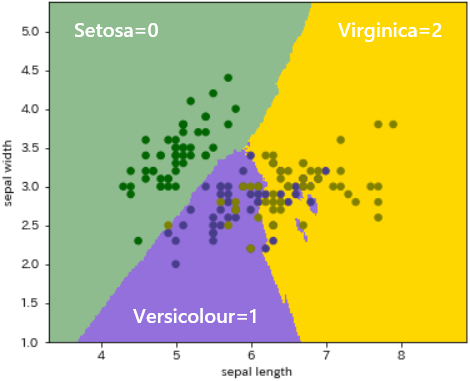
- これをもとにコンター図(等値線図)を描画し、併せて個々のデータをプロットします。
plt.figure(figsize=(6,5))
# 等値線図
plt.pcolormesh(xx, yy, Z, cmap=cmap_surface)
# 散布図
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_dot, s=30)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.show()
- matplotlibの
pcolormesh()関数は、不定形な長方形グリッドをもとにカラープロットを生成します。 - 引数を単純に
(x, y, Z, c)とすると、左からx, yがメッシュの座標です。その中をセル毎にグループの情報を持ったデータZ、これにcで色を割り当てています。
あとがき
- この例ではグループ1と2が交錯ぎみで、飛び地も見られます。ただし、分析軸(特徴量の組合せ)を変えるとマップの表情は大いに異なり、予測による領域とデータが共にグループ間で明確に分割されてきます。より効果的な分析軸が視覚的にとらえられます。
- なお、手順として、まず k の最適値を見定めることが大切ですね。