Quantum Native Dojoで紹介されている5-1. Variational Quantum Eigensolver(VQE)アルゴリズム と 6-2. Qulacs を用いた variational quantum eigensolver (VQE) の実装を参考に、H-He+の基底状態のエネルギー固有値をVariational Quantum Eignesolver(VQE)により求めました。n番煎じですが、本稿でまとめたいと思います。
まず、VQEについて解説した後、VQEで必要なHamiltonianと変分量子状態を準備する方法を説明します。その後、実際にVQE実装した時のコードと結果を書き連ねていこうと思います。
1. Variational Quantum Eigensolver(VQE)
VQEは、変分法によりHamiltonianの基底状態のエネルギー固有値を求めるアルゴリズムの一つです。このアルゴリズムは、量子力学の変分原理に基づいています。
変分原理とは、
時間依存のないShoredinger方程式(TISE) $\mathcal{H}\Phi = \epsilon\Phi $ の解 $ \Phi $ は、Hamiltonianの期待値
$$
{
\begin{align}
\epsilon[\Phi] := \frac{<\Phi|\mathcal{H} |\Phi>}{<\Phi|\Phi>}
\end{align}
}
$$
に停留値を取らせるようなものであり、その停留値が$\mathcal{H}\Phi = \epsilon\Phi $の固有値$\epsilon$である、
という主張です。
最小値は極小値であるとすれば、変分原理により、その最小の$\epsilon$が基底状態のエネルギー固有値であり、$\epsilon $を最小にする関数は基底状態の固有関数を表すといえます(真面目な議論はこちらに)。
このことを利用して、変分法による基底状態のエネルギー固有値の計算では、TISEの解の候補にパラメータで指定される量子状態を用いて、Hamiltonianの期待値を計算し、最小値が得られるようにパラメータを最適化します。
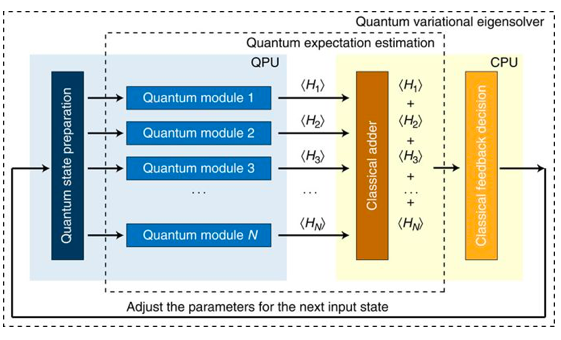
VQEでは、図1で示すようにパラメータで指定された量子状態の用意とHamiltonianの期待値の計算 を量子コンピュータ(もしくはシミュレータ)で行い、パラメータの最適化を古典コンピュータで実行します。
$ < H_i > (i=1,2…N)$ は、Hamiltonianを量子回路で表現できる形に分解したときの、各項の期待値です(Hamiltoninanの分解方法は、次の節で説明します)。Hamiltonianの期待値の計算方法には、実際にq-bitを何度か計測して推定する方法、もしくはシミュレータで計算する方法の2通りがあります。今回は、量子コンピュータのシミュレーションにQulacsを用いて、期待値を計算します。
2. H-He+のHamiltonian
分子のHamiltonianは、次のように与えられます。
{\begin{align}
\mathcal{H} &= -\sum_i\frac{\hbar^2}{2m_e}\nabla^2_i +\frac{1}{2}\sum_{i\neq j}\frac{e^2}{4\pi \epsilon_0}\frac{1}{|\boldsymbol{r}_i - \boldsymbol{r}_j|} \\
&-\sum_I\frac{\hbar^2}{2M_I}\nabla^2_I + \frac{1}{2}\sum_{I\neq J}\frac{e^2}{4\pi \epsilon_0}\frac{Z_I Z_J}{|\boldsymbol{R}_I - \boldsymbol{R}_J|} - \sum_{i,I}\frac{e^2}{4\pi \epsilon_0} \frac{Z_I}{|\boldsymbol{r}_i - \boldsymbol{R}_I|}
\end{align}
}
これにBorn-Oppenheimer近似を施して核と電子の運動を分離し、これからは核の位置を固定した際の電子系のHamiltonian
{\begin{align}
\mathcal{H}_e = -\sum_i \frac{\nabla^2_i}{2} -\sum_{i, I}\frac{Z_I}{|\boldsymbol{r}_i - \boldsymbol{R}_I|} + \frac{1}{2}\sum_{i\neq j}\frac{1}{|\boldsymbol{r}_i - \boldsymbol{r}_j|}
\end{align}
}
を考えます。第一項・第二項は一体の演算子で、第三項は二体の演算子です。
これをさらに、第二量子化することで、
{\mathcal{H_e} = \sum_{pq}h_{pq}a^{\dagger}_pa_q + \frac{1}{2}\sum_{pqrs}h_{pqrs}a^{\dagger}_pa^{\dagger}_qa_ra_s
}
と書けます。第一項が一体の演算子に、第二項が二体の演算子に対応します。
第二量子化されたHamltonianの係数は、以下のように計算できます。
{h_{pq} = \int d \tau \phi^*(\tau)\left(-\frac{\nabla^2_\boldsymbol{r}}{2}-\sum_I\frac{z_I}{| \boldsymbol{R}_I-\boldsymbol{r} |} \right) \phi_q (\tau)\\
h_{pqrs} = \int d \tau_1 d \tau_2 \phi^*_p(\tau_1)\phi^*_q(\tau_2)\frac{1}{\boldsymbol{r}_1-\boldsymbol{r}_2}\phi_s(\tau_1)\phi_r(\tau_2)
}
この計算は量子化学計算ソフトにより行われます。
第二量子化されたHamltonianを量子コンピュータで扱える形にするために、Jordan-Wigner(JW)変換もしくはBraviy-Kitaev(BK)変換を執り行います。これらの変換では、生成消滅演算子をパウリ演算子のテンソル積に置き換えます。それゆえ、Hamiltonianはパウリ演算子のテンソル積の和で書き表されます。量子回路では、ユニタリーであるパウリ演算子を量子ゲートとして量子状態に作用できるので、JW/BK変換によりHamiltonianは量子状態に作用できる形になります。
以上の過程を経ることで、H-He+間の核間距離が0.9 Åの時のHamiltonianは次のように書けます。Hamiltonianを構成する具体的なパウリ演算子やその係数は、参考にした論文のSupplementary InformationのTable2から持ってきました。
M = (-3.8505 * I - 0.2288 * X1 - 1.0466 * Z1 - 0.2288 * X0 + 0.2613 * X0 * X1 + \
0.2288 * X0 * Z1 - 1.0466*Z0 + 0.2288* Z0 * X1 + 0.2356 * Z0 * Z1 )/2
3. 変分量子状態の準備
初期化した量子状態$|00>$にパラメトリックな量子回路を作用させて、変分量子状態を用意します。
5-1. Variational Quantum Eigensolver(VQE)アルゴリズムでは、論文A. Peruzzo et al. , “A variational eigenvalue solver on a photonic quantum processorと同様な変分量子回路を用いています。本稿でも、それに倣います。
0_0 --RX(phi[0])--RZ(phi[1])--CX---------------------------
0_1 --RX(phi[2])--RZ(phi[3])--・---RZ(phi[4])--RX(phi[5])--
RX,RZは回転ゲートで、CXは制御NOTゲートです。制御NOTゲートでは、黒点の方が制御q-bitになります。
量子コンピュータ(or量子シミュレータ)で得るHamiltonianの期待値が最小値になるよう、この変分量子回路のパラメータを古典的に最適化していきます。
4. VQEの実装
4.1 ライブラリのインストールとインポート
## Google Colaboratory上で実行する場合バグを回避するためscipyをダウングレード
!pip install scipy==1.2.1
## 各種ライブラリがインストールされていない場合は実行してください
## Google Colaboratory上で実行する場合'You must restart the runtime in order to use newly installed versions.'と出ますが無視してください。
## runtimeを再開するとクラッシュします。
!pip install qulacs openfermion
# 必要なライブラリのインポート
from openfermion.transforms import get_fermion_operator, jordan_wigner, bravyi_kitaev
from openfermion.transforms import get_sparse_operator
from openfermion.utils import get_ground_state
import numpy as np
import matplotlib.pyplot as plt
Quantum Native Dojoに従います。私は、Google Colaboratory上で行いましたが、自前の環境がある方はそちらでも構わないと思います。
4.2 Pauli演算子でHamiltonianを表す。
from openfermion.ops import QubitOperator
I = QubitOperator('')
X0 = QubitOperator('X0')
X1 = QubitOperator('X1')
Y0 = QubitOperator('Y0')
Y1 = QubitOperator('Y1')
Z0 = QubitOperator('Z0')
Z1 = QubitOperator('Z1')
M = (-3.8505 * I - 0.2288 * X1 - 1.0466 * Z1 - 0.2288 * X0 + 0.2613 * X0 * X1 + \
0.2288 * X0 * Z1 - 1.0466*Z0 + 0.2288* Z0 * X1 + 0.2356 * Z0 * Z1 )/2
print(M)
OpenFermionは、Googleが配布している量子化学計算用のPythonライブラリです。OpenFermionのQubitOperatorを用いて、仕方なしに量子回路で表現できるHamiltonianを手打ちで入れています。
わざわざ手でHamiltonianを入力せずに、核間距離だけからOpenFermionによる量子化学計算でHamiltonianを求められるはず Openfermion-PySCFにより量子化学計算でOpenfermion形式のHamiltonianを求められるはず ですが、僕はうまくできませんでした。ご存知の方教えてください……
1/19/2020
multiplicity = 1 and charge = 1としてHeHの計算をPySCFで行えばよいです。コメント参照。
4.3 HamiltonianをQulacsの扱える形に変える。
from qulacs import Observable
from qulacs.observable import create_observable_from_openfermion_text
qulacs_hamiltonian = create_observable_from_openfermion_text(str(M))
Qulacs では、Hamiltonianは Observable クラスによって扱われます。Qulacsには、OpenFermion のHamiltonianを Qulacs の Observable に変換する関数create_observable_from_openfermion_text が用意されているので、これを使います。
4.4 変分量子回路を定義する。
from qulacs import QuantumState, QuantumCircuit
from qulacs.gate import CNOT, RX, RY, RZ, merge
n_qubit = 2
n_param = 6
def ansatz_circuit(theta_list):
"""ansatz_circuit
Returns ansatz circuit.
Args:
theta_list (:class:`numpy.ndarray`):
rotation angles.
Returns:
:class:`qulacs.QuantumCircuit`
"""
circuit = QuantumCircuit(n_qubit)
for i in range(n_qubit):
circuit.add_gate(merge(RX(i, theta_list[i*2]), RZ(i, theta_list[1+2*i])))
circuit.add_gate(CNOT(1, 0))
circuit.add_gate(merge(RZ(1, theta_list[4]), RX(1, theta_list[5])))
return circuit
4.5 変分量子状態に対してHamiltonianの期待値を計算する関数を定義する。
def cost(theta_list):
state = QuantumState(n_qubit) #|00> を準備
circuit = ansatz_circuit(theta_list) #量子回路を構成
circuit.update_quantum_state(state) #量子回路を状態に作用
exp_value = qulacs_hamiltonian.get_expectation_value(state) #ハミルトニアンの期待値を計算
# print('energy = ',exp_value)
return (exp_value)
Cost関数とも呼ばれます。
4.6 VQEを実行する。
from scipy.optimize import minimize
cost_history = []
init_theta_list = np.random.rand(n_param)
cost_history.append(cost(init_theta_list))
method = "BFGS" #powellもok
options = {"disp": True, "maxiter": 50, "gtol": 1e-6}
opt = minimize(cost, init_theta_list,
method=method,
callback=lambda x: cost_history.append(cost(x)))
plt.rcParams["font.size"] = 18
plt.plot(cost_history, color="red", label="VQE")
plt.xlabel("Iteration")
plt.ylabel("Energy expectation value")
plt.legend()
plt.show()
最適化には、scipyに実装されているBFGS法もしくはpowell法を用います。
ここまでのプログラムを実行すると、initial parametersによりますが、図2に示すように収束する結果が得られると思います。
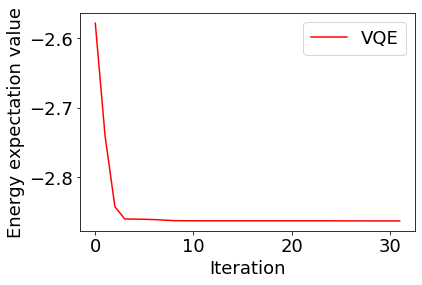
図2:VQEによるH-He+の基底状態のエネルギー固有値の計算
4.7 厳密対角化と比較する。
print(cost_history[len(cost_history)-1])
sparse_M_matrix = get_sparse_operator(M)
print(get_ground_state(sparse_M_matrix)[0])
>>>
-2.8623984255667687
-2.8626207640766843
結果の上段がVQEにより、下段が厳密対角化により得た値です。小数点以下第3位まで一致しています。基底状態とその固有値を近似的に求めることに成功したと言って、差支えないのではないでしょうか。やったね!!!
5. 参考
以下の記事・論文を参考にしました。
・[1] A. Peruzzo et al. , “A variational eigenvalue solver on a photonic quantum processor Nat. Commun. 5:4213 doi: 10.1038/ncomms5213 (2014)
・5-1. Variational Quantum Eigensolver(VQE)アルゴリズム
・6-2. Qulacs を用いた variational quantum eigensolver (VQE) の実装
・SSVQEを用いて励起状態との遷移行列を計算してみた。
VQEについて非常に詳しく、VQEの発展形であるSSVQEについても書かれている。
・R. Babbush and J. McClean, “Announcing OpenFermion: The Open Source Package for Quantum Computers”, Google AI Blog,
OpenFerimonのGoogle自らの紹介記事です。
・はじめての量子化学計算:水素化ヘリウムイオンの基底エネルギーを計算してみた
自作のシミュレータで、同様のことを行っていた方。すごい…。
6. 次に読みたいもの
・量子超越性に関する論文紹介 ~Variational Quantum Eigensolver~
上に挙げた論文を詳しく紹介している。
・VQEのansatzに使うUnitary Coupled Cluster 法を再現する回路の例
今回なぜ上のような変分量子回路を用いたのか理解できなかったので、その理由を知りたい。
・VQEは既存の量子化学計算を超えるだろうか? ~精度と計算リソースの見積もり~
VQEと古典コンピュータを用いた量子化学計算との比較がされている。
・量子コンピュータで量子化学計算
良くまとめられているので、理解を深めたい。
・Quantum Algorithms: Variational-Quantum-Eigensolver
英語の解説記事です。
7. 疑問点・メモ
・実際の量子コンピュータでどのように期待値を計算するのか理解できていない。
・古典的な最適化について調べる。
・JW/BKについても調べる。
・第二量子化あたりをもうちょっと解説したい。