量子超越性に関する論文紹介 ~Variational Quantum Eigensolver~

今回は、量子超越性を実証する上で重要な手法である Variational Quantum Eigensolver について提唱論文¹に沿って紹介します。

はじめに

最近、量子コンピュータに関するニュースをよく見聞きします。GoogleとIBMは、50~70個の量子ビットからなる量子ゲート型プロセッサの開発でしのぎを削っています²³。IBMは、クラウド上で量子コンピュータを利用できるサービス IBM Q を公開しています⁴。また、Microsoftは、量子コンピュータ向けのプログラミング言語 Q# を開発して公開しています。

とは言うものの、誤り訂正符号も備えた汎用量子コンピュータの実現には数百万量子ビットを搭載したプロセッサが必要であり、その実現には未だ程遠い状況です。現状の量子コンピュータに使い道はないのでしょうか？

量子超越性とは

量子コンピュータが古典コンピュータと比べて優位な点は、量子ビットの重ね合わせ状態や絡み合い状態を利用することで超並列処理が可能となることです。こうした量子コンピュータの優位性に特化することで、現状の100個に満たない量子ビットからなるプロセッサでも古典コンピュータに対する優位性（量子超越性, quantum spremacy）を証明することができそうです。

そうした試みの一つとして、現状の技術で実現可能な量子プロセッサと古典コンピュータを組み合わせて、量子化学計算などの大規模な固有値問題を解く方法（Variational Quantum Eigensolver）が研究されています。今回は、この手法を提唱した論文を紹介します¹。※IBM による最近の発展も含めた詳細なレビューもあります⁵。

論文紹介：A variational eigenvalue solver on a photonic quantum processor

書誌情報

タイトル：A variational eigenvalue solver on a photonic quantum processor
著者：A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik, J. L. O'Brien
掲載雑誌：Nature Communications, Volume 5, id. 4213 (2014).
https://arxiv.org/pdf/1304.3061.pdf

論文の概要

量子化学計算などでは、次元数が自由度の指数オーダーで大きくなる固有値問題を扱います。こうした大規模問題を量子コンピュータのみで解こうとすると、コヒーレンスを維持した多数の量子ビットと量子演算が必要となり、現状規模の量子プロセッサでは解けません。

この困難を解決するため、固有値問題を
１．量子状態として準備した固有ベクトルにより固有値を計算する部分と、
２．計算された固有値を最適化して量子状態を更新する部分
とに分解します。量子プロセッサは得意な固有値計算（前者）だけに特化し、最適化計算（後者）は古典コンピュータに任せることで、現状の量子プロセッサでも量子超越性を実証できるというのが論文のアイデアです。

論文ではフォトン（光の量子）を使った量子プロセッサ（QPU）とCPUを結合したプロトタイプを実装して、２原子分子 He-H+ の基底状態のエネルギーを計算できることを実証しています。

図１：VQEのアーキテクチャ

他にもどんな問題に使えるのか？

ノード数に対して状態数が指数オーダーとなるような固有値問題への適用が考えられます。この論文では、検索エンジンによるインターネット探索、新物質や新薬のデザインなどを例として挙げていますが、他にも巡回セールスマン問題などの最適化問題（NP完全問題）にも適用できます。

これまでのアプローチの問題点

古典コンピュータでは扱えない大規模な固有値問題を解く量子アルゴリズムとしては、量子位相推定（QPE, Quantum Phase Estimation）が知られています。この手法は、古典的手法に比べて指数オーダーで処理が速くなりますが、測定精度（誤差の大きさ）$\epsilon$ を実現するには、$O(1/\epsilon)$ の回数だけ量子演算が必要となります。実用に耐えうる精度を実現するには、数百万~数十億個の量子ゲートが必要となってしまいます。

そこで QPE に代わる実現可能な手法として、本論文では QPU によりハミルトン関数（Hamiltonian）$H$ の変分状態関数 $|\psi(\theta)\rangle$ の生成および期待値 $E(\theta):=\langle\psi(\theta)|H|\psi(\theta)\rangle$ の計算を行い、CPUによりエネルギー期待値 $E(\theta)$ を最小化するよう変分パラメータ $\theta$ を更新するというハイブリッド手法を提唱しています。

アルゴリズム１: 量子期待値計算

アルゴリズム１では、QPUによりハミルトン関数（Hamiltonian）に含まれる演算子積の期待値を計算し、CPUによりそれら期待値を足し上げます。ハミルトン関数は、物理系のエネルギー（あるいは機械学習のコスト関数）をあたえる演算子で、その最小固有値と固有ベクトルは、物理系の基底状態（あるいは機械学習の最適解）に対応します。

VQEでは、量子化学計算における分子軌道上の電子や、最適化問題における離散変数を、量子ビットで置き換えて状態関数をシミュレートします。そのため、ハミルトン関数 $\cal H$ は、複数の量子ビットに作用するパウリ行列の直積和として書き換えられます。※量子ビットやパウリ行列については、この記事の最後にある補足を参照してください。

\begin{equation}
{\cal H} = \sum_{i\alpha} h_\alpha^i\,\sigma_\alpha^i
+\sum_{ij\,\alpha\beta} h_{\alpha\beta}^{ij}\,\sigma_\alpha^i \sigma_\beta^j +\dots
\end{equation}

ここで、$\sigma_\alpha^i$ は、i 番目の量子ビットに作用するパウリ行列の $\alpha$ 成分（例えば $\alpha=x$）を意味します。さらに入力状態 $|\psi\rangle$ について期待値を計算します（次式）。

\begin{align}
\langle{\cal H}\rangle &= \sum_{i\alpha} h_\alpha^i\,
\langle\sigma_\alpha^i\rangle
+\sum_{ij\,\alpha\beta} h_{\alpha\beta}^{ij}\,
\langle\sigma_\alpha^i \sigma_\beta^j\rangle +\dots
\end{align}

量子ビット数を $n$ とすると、ハミルトン関数とその期待値はパウリ行列の $n$ 重直積からなる多項式およびその期待値として記述されます。このとき、状態ベクトル $|\psi\rangle$ の次元数は $2^n$ となり、ハミルトン関数の期待値を求める問題は $2^n \times 2^n$ 行列の固有値問題に帰着します。

古典コンピュータでハミルトン関数の期待値（上式）を計算する場合を考えてみます。この場合、指数オーダーの次元数からなる入力状態を一度に定義することはできないので、個別のパウリ行列積（局所ハミルトン関数）が作用する量子ビットだけを含む部分状態について期待値を計算することになります。

最終的には、このように個別に計算した期待値から、それら期待値すべてを導くことができる入力状態 $|\psi\rangle$ を決定する必要があります。この問題は、QMA困難（NP困難の拡張クラス）であり、古典計算でも量子計算でも解くのが難しい問題です（N表現可能性問題（N-representability problem）として知られています）⁶。

VQEによる量子計算では、QPUを使って大域的な入力状態 $|\psi\rangle$ を直接生成して、ハミルトン関数の各項の期待値を計算するのでN表現可能性問題を回避できます。

アルゴリズム２：量子変分固有値ソルバー

アルゴリズム１の期待値計算では、状態関数は真の基底状態の良い近似になっている必要があります。断熱発展や量子メトロポリス法など、これまでの近似方法はいずれも長いコヒーレンス時間を必要とする問題点があります。

アルゴリズム２では、上述の問題点を回避するため状態関数を変分法により近似します。具体的には、状態関数を変分パラメータ $\theta$ を引数とする変分近似関数 $|\psi(\theta)\rangle$ として表し、アルゴリズム１を用いてエネルギー期待値 $E(\theta)$ を計算します。さらに、$E(\theta)$ を最小化するように変分パラメータ $\theta$ を更新します。

アルゴリズム１とアルゴリズム２を $E(\theta)$ が収束するまで交互に繰り返すことで、変分近似関数は自ずと真の基底状態に近づいていきます。量子状態のコヒーレンスは期待値計算の間だけ維持できれば良いので、従来法の問題点を回避することができます。

プロトタイプの解説

VQEのプロトタイプは、図２にある通りQPUとCPUを結合したハイブリッド構造のプロセッサです。

図２：提案方式の実験用実装

QPUは、フォトンの偏光を量子ビットとして利用したものです。量子回路を構成する量子ゲートは、偏光分離器と位相変位器を使って実装されています。フォトンの独立な2つの偏光状態をそれぞれ $|0\rangle$, $|1\rangle$ と定義すると、偏光分離器はアダマール（Hadamard）ゲートの役割をしています。

H = \dfrac{1}{\sqrt{2}}\left(
\begin{matrix} 1 & 1 \\ 1 & -1\end{matrix}\right)

また、位相変位器は０状態はそのままで１状態の位相のみシフトするので、以下の量子ゲートに対応します。

P_\phi = \left(\begin{matrix} 1 & 0 \\ 0 & e^{i\phi}\end{matrix}\right)

さらに、図３の中央にある偏光分離器を３個つなげた部分（四角枠で囲った部分）は制御Zゲートという量子ゲートの役割を果たします。この制御ZゲートのZゲートは、Hゲートで挟まれいるので、パウリ行列の演算則から制御NOTゲートと等価になることが分かります⁷。

図３：QPUの制御NOTゲート

この量子プロセッサのしくみを量子回路で表すと以下の図のようになります。

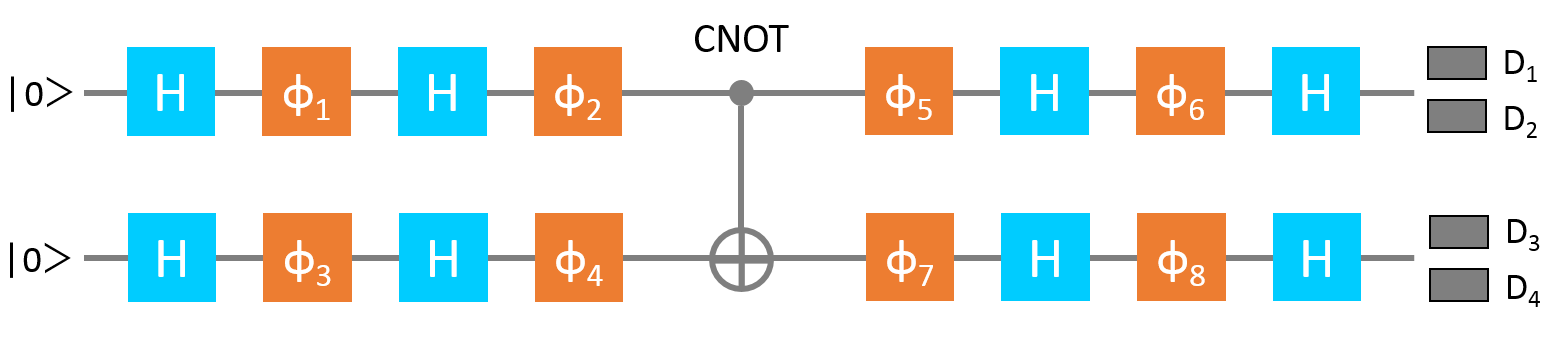図４：QPUの量子回路図

２つの入力光子にアダマール変換と位相シフトを行うことで、それぞれの光子は、０状態と１状態の重ね合わせ状態となります。その後、中央の制御NOTゲートを介して、２つの重ね合わせ状態は互いに絡み合い状態（entanglement states）となります。８個の位相シフトは、状態関数だけではなく演算子 $\sigma_z^i \otimes \sigma_z^j$ を測定する準備にも使用されているので、その自由度を除いた残りが変分パラメータ $\theta$ として状態関数 $|\psi(\theta)\rangle$ を生成します。

この状態関数を、QPUの出力にある検出器で観測することにより、期待値 $\langle\psi(\theta)|\sigma_z^i \otimes \sigma_z^j|\psi(\theta)\rangle$ が計算できます。この結果は図３右側のCPUに渡されてエネルギー関数に足し上げられ、最適化計算を経て変分パラメータ $\theta$ が更新されます。更新された $\theta$ はQPUに渡されて（図３のCPUからQPUに向かう８本の矢印）計算ステップが繰り返されます。

プロトタイプによるデモ計算

実験では、上述の光子を使った２量子ビットのプロセッサを用いて２原子分子 He-H+ の基底状態のエネルギーを計算しています。

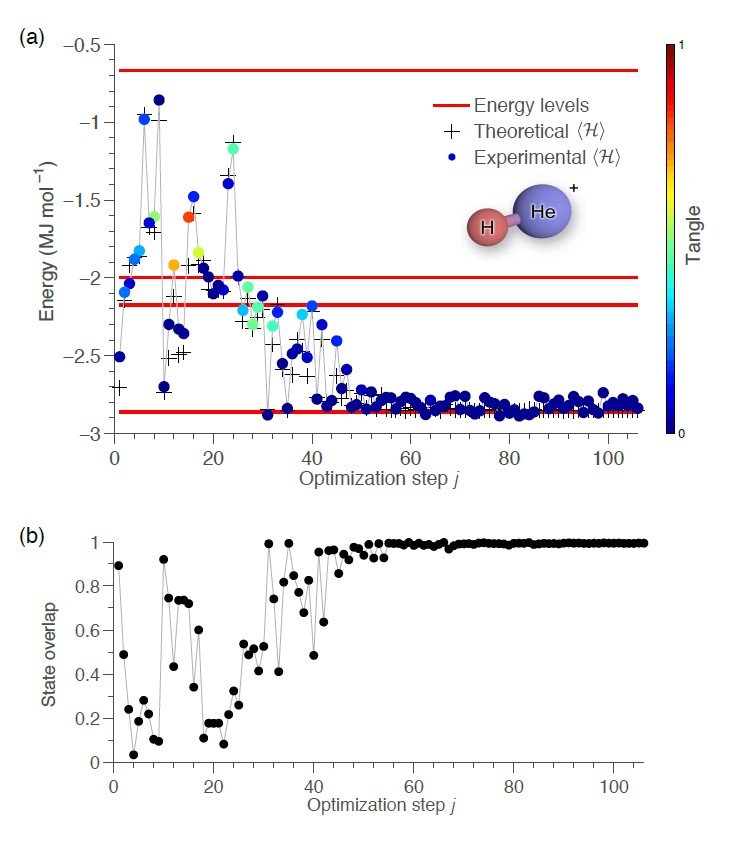図５：He-H+ の基底状態エネルギーの探索

２原子分子のハミルトン関数は、Born-Oppenheimer近似により原子間距離 $R$ を外部パラメータとする２電子系のエネルギー関数と記述できます。第２量子化ハミルトン関数において、電子の生成・消滅演算子に対してJordan-Wigner変換を施すことにより、ハミルトン関数は以下の様に記述できます（詳細はAppendixを参照）。

\begin{equation}
{\cal H}(R) = \sum_{i\alpha} h_\alpha^i (R)\,\sigma_\alpha^i
+\sum_{ij\,\alpha\beta} h_{\alpha\beta}^{ij}(R)\,\sigma_\alpha^i \sigma_\beta^j
\end{equation}

ここで、係数 $h_\alpha^i (R)$, $h_{\alpha\beta}^{ij}(R)$ は、Appendix の積分式をもとに PSI3 パッケージなどを使って数値計算できます。

図５は、原子間距離 $R=90,{\rm pm}$ の場合に、He-H+ の基底状態を調べたものです。図５(a) は、デモ実験で計算した基底状態エネルギーを最適化のステップ数に対してプロットしたものです。ドットはデモ計算の値で、色の違いは基底状態関数の絡み合いの度数を表しています。クロスは、理論計算による値です（量子ビットが少ないので理論計算できます）。赤い線は、軌道電子のエネルギー準位（これも理論値）です。ドットの振る舞いを見ると最適化のステップが進むにつれてデモ計算値が基底状態エネルギーに収束しているのが分かります。

図５(b) は、デモ計算の j-ステップにおける状態関数 $|\psi^j\rangle$ と理論計算による基底状態関数 $|\psi^G\rangle$ との重複度 $|\langle\psi^j|\psi^G\rangle|$ を最適化ステップ数 j に対してプロットしたグラフです。最適化ステップが進むにつれて重複度が１に収束していく（つまり、デモ計算の状態関数が真の基底状態に近づいていく）様子が分かります。

図６：He-H+ の結合解離曲線

図６は、He-H+ の結合解離エネルギーを原子間距離 $R$ についてプロットしたグラフです。上のグラフの $R=(80,100),{\rm pm}$ の区間を切り出して拡大したのが下のグラフです。紺色のドットは、デモ実験の数値に実験誤差を考慮して修正した値を表しています。修正後のデモ実験値が、赤色の理論曲線を再現するように並んでいます。デモ実験値（ドット）を曲線回帰して結合解離エネルギーが最小となる原子間距離を計算すると $R=92.3\pm0.1,{\rm pm}$ となり、エネルギー値は $E=-2.865\pm0.008,{\rm MJ/mol}$ と計算されます。この値は、基底状態エネルギーの理論値と一致します。

まとめ

量子化学計算など量子ビット数 $n$ の指数オーダーの次元を持つ固有値問題を、効率よく計算する手法としてVQEを提唱しました。

VQEは、量子期待値計算と量子変分固有値ソルバーの２つのアルゴリズムから構成されます。量子期待値計算では、従来法である量子位相推定（QPE）に比べて短いコヒーレンス時間で済むので、少ないリソース（量子ビットおよび量子ゲート）で効率よく計算できます。

また、デモで実施したに２量子ビット系の場合、QPEでは12個のCNOTゲートが必要となりますが、量子変分固有値ソルバーでは、８個の位相変換器と１個のCNOTゲートで済みます。また、変分パラメータで記述される状態ベクトルを直接計算に用いるのでN表現可能性問題を回避することができます。

Appendix

量子化学計算の場合、ハミルトン関数は分子軌道上にある電子の運動エネルギーと相互作用エネルギーの和として記述されます。電子の波動場を量子化する第２量子化の立場では、ハミルトン関数は電子の生成・消滅演算子 $\hat{a}_p^\dagger$, $\hat{a}_p$（$p$ は電子状態を表す添字）を用いて以下の様に記述されます。

\begin{equation}
{\cal H}(R) = \sum_{pq} h_{pq}(R)\,\hat{a}_p^\dagger \hat{a}_q
+\sum_{pqrs} h_{pqrs}(R)\,\hat{a}_p^\dagger \hat{a}_q^\dagger \hat{a}_r \hat{a}_s
\end{equation}

ここで $R$ は、ハミルトン関数の係数を決める外部パラメータです。この論文で扱っている He-H+ のような２原子分子の場合、$R$ は２原子間距離を表しており、係数関数は以下の様に計算されます。

\begin{align}
h_{pq}(R) &= \int dr\,\chi_p(r)^* \left(-\frac{1}{2} \nabla^2
 -\sum_a \dfrac{Z_a}{|r_a -r|}\right)\chi_q(r) \\
h_{pqrs}(R) &= \int dr_1\,dr_2\, \dfrac{\chi_p(r_1)^* \chi_q(r_2)^* \chi_r(r_1) \chi_s(r_2)}{|r_1 -r_2|}
\end{align}

Born-Oppenheimer近似により２原子核の情報は、２原子間距離 $R$ と２つの原子核の電荷量 $Z_1, Z_2$ に集約されます。$h_{pq}(R)$ は、２電子の運動エネルギーと原子核から受けるクーロンポテンシャル、$h_{pqrs}(R)$ は、２電子間のクーロンポテンシャルに対応するエネルギー係数です。

第２量子化ハミルトン関数を量子プロセッサで計算するには、ハミルトン関数に現れる電子の生成・消滅演算子を量子ゲート演算子にマッピングする必要があります。これは、以下の Jordan-Wigner変換により計算できます。

\begin{align}
\hat{a}_j &\to I^{\otimes j-1}\otimes\sigma_+ 
\otimes\sigma_z^{\otimes N-j}\\
\hat{a}_j^\dagger &\to I^{\otimes j-1}\otimes\sigma_- 
\otimes\sigma_z^{\otimes N-j}
\end{align}

ただし $\sigma_\pm = (\sigma_x \pm i\sigma_y)/2$ を定義しています。
パウリ行列の演算を行うことで以下の対応を確かめることができます。

\begin{align}
\hat{a}_p^\dagger \hat{a}_p &\to I - \sigma_z^p\\
\hat{a}_p^\dagger \hat{a}_p \hat{a}_q^\dagger \hat{a}_q &\to 
I -\sigma_z^p -\sigma_z^q -\sigma_z^p \sigma_z^q
\end{align}

これにより、２電子系のハミルトン関数が本文にあるようにパウリ行列の１次および２次の項で表されることが分かりました。

補足：量子ビットの表現について⁸

量子論理では、情報量の基本単位は量子ビットであり、これは複素２次元空間のベクトル $|\psi\rangle \equiv \left({\psi_1 \atop \psi_2}\right)$ として定義されます。このベクトルの共役ベクトルは、$\langle \psi| \equiv (\psi_1^{*}, \psi_2^{*})$ として定義されます。任意の２つの量子ビット $|\psi\rangle$ と $|\phi\rangle$ の内積は $\langle\phi|\psi\rangle\equiv\phi_1^* \psi_1 +\phi_2^* \psi_2$ と定義されます。

量子ビットの基底ベクトルとして $|0\rangle\equiv\left({1 \atop 0}\right)$ と $|1\rangle\equiv\left({0 \atop 1}\right)$ を定義すると、任意の量子ビットは $0$ 状態 $|0\rangle$ と $1$ 状態 $|1\rangle$ の重ね合わせ状態を表しています。

$$
|\psi\rangle = \left({\psi_1 \atop \psi_2}\right)
= \psi_1 \left({1 \atop 0}\right) +\psi_2 \left({0 \atop 1}\right)
= \psi_1 |0\rangle + \psi_2 |1\rangle
$$

量子ビットのノルム $\langle\psi|\psi\rangle\equiv|\psi_1|^2 +|\phi_2|^2$ を不変にするユニタリー変換群は $SU(2)$ と呼ばれ、３次元回転群の２価表現となっています。

したがって量子ビットに対する演算操作を定義する量子ゲートは、$2\times2$ 単位行列とパウリ行列（Pauli matrices）により生成されます。

I =\left(\begin{matrix} 1 & 0 \\ 0 & 1\end{matrix}\right), \quad
\sigma_x = \left(\begin{matrix} 0 & 1 \\ 1 & 0\end{matrix}\right), \quad
\sigma_y = \left(\begin{matrix} 0 & -i \\ i & 0\end{matrix}\right), \quad
\sigma_z = \left(\begin{matrix} 1 & 0 \\ 0 & -1\end{matrix}\right).

例えば $\sigma_x$ は、量子ビット $|0\rangle\equiv\left({1 \atop 0}\right)$ と $|1\rangle\equiv\left({0 \atop 1}\right)$ を交換するNOTゲートを定義します。

\sigma_x |0 \rangle = 
\left(\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}\right) 
\left({1 \atop 0} \right) = \left({0 \atop 1}\right)
= |1\rangle

パウリ行列の２乗は単位行列に等しく、パウリ行列の２成分の積は、残りの１成分に位相因子を除いて等しくなります。

\sigma_x^2 = \sigma_y^2 = \sigma_z^2 = I, \quad
\sigma_x \sigma_y = i\sigma_z,\quad \sigma_y \sigma_z = i\sigma_x,\quad
\sigma_z \sigma_x = i\sigma_y.

パウリ行列による量子演算を以下の図にまとめした。

演算子 $H\equiv {1\over\sqrt{2}}\left(\sigma_x + \sigma_z\right)$ は、アダマールゲート（Hadamard gate）と呼ばれる演算子で、$|0 \rangle$ または $|1 \rangle$ に作用して、両ベクトルの重ね合わせ状態¹を生成します。

H |0 \rangle = \dfrac{1}{\sqrt{2}}
\left(\begin{matrix} 1 & 1 \\ 1 & -1 \end{matrix}\right) 
\left({1 \atop 0} \right) = \dfrac{1}{\sqrt{2}}\left({1 \atop 1}\right)
= \dfrac{1}{\sqrt{2}}\left(|0\rangle+|1\rangle\right)

$n$ 個の量子ビットが表現する状態ベクトルは、必ずしも $n$ 個の量子ビットの直積で表される状態だけでなく、$n$ 個の量子ビットが互いに絡み合った状態（entanglement states）も含まれています。このような絡み合い状態を実現する最も簡単な量子ゲートとして、制御NOTゲート（Controlled NOT, CNOT）があります。

CNOTゲートは、２量子ビットを入力とする量子ゲートで、制御ビット入力が０状態のとき目標ビットは入力のままですが、制御ビット入力が１状態のとき、目標ビットは反転されます。制御ビットの値に応じて目標ビットにNOT演算が作用するので制御NOTゲートと呼ばれます。

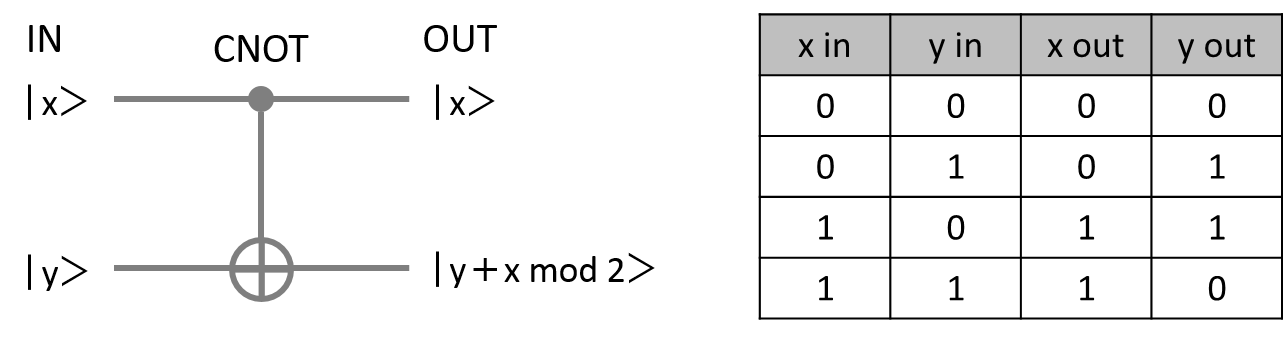
制御ビットが０状態と１状態の重ね合わせ、目標ビットが０状態にある２量子ビット入力に、CNOTゲートを作用させると絡み合い状態 $|00\rangle+|11\rangle$ が出力されます。

\left(|0\rangle+|1\rangle\right)\otimes|0\rangle 
= |00\rangle+|10\rangle \xrightarrow{CNOT} |00\rangle+|11\rangle

参考文献

1. A. Peruzzo et al, "A variational eigenvalue solver on a photonic quantum processor", Nature Communications, Volume 5, id. 4213 (2014). https://arxiv.org/abs/1304.3061 ↩ ↩² ↩³

2. Quantum Computing: Breaking Through the 49 Qubit Simulation Barrier https://www.ibm.com/blogs/research/2017/10/quantum-computing-barrier/ ↩

3. Google thinks it’s close to “quantum supremacy.” Here’s what that really means. https://www.technologyreview.com/s/610274/google-thinks-its-close-to-quantum-supremacy-heres-what-that-really-means/ ↩

4. IBM は、現在 20 量子ビットの量子コンピューター IBM Q をクラウド上で公開しています。https://www.ibm.com/developerworks/jp/cloud/library/cl-quantum-computing/index.html ↩

5. Nikolaj Moll et al, "Quantum optimization using variational algorithms on near-term quantum devices", Quantum Sci. Technol. 3 030503 (2018). https://arxiv.org/abs/1710.01022 ↩

6. Y.-K. Liu, M. Christandl, and F. Verstraete, "N-representability is QMA-complete", Phys. Rev. Lett. 98, 110503 (2007). https://arxiv.org/abs/quant-ph/0609125 ↩

7. A. Politi, J. C. F. Matthews, nd J. L. O'Brien, "Shor's quantum factoring algorithm on a photonic chip", Science, Vol.325, p.1221 (2009). https://arxiv.org/abs/0911.1242 ↩

8. 中山 茂著「量子アルゴリズム」技報堂出版（2014） ↩