VQEの論文では，天下り的にansatzを作る回路が書かれていることが多いので，どうやって一から作ればいいのか考えてみる．
参考
- How to prepare Unitary Coupled-Cluster ansatz for VQE in a circuit?
https://quantumcomputing.stackexchange.com/questions/9049/how-to-prepare-unitary-coupled-cluster-ansatz-for-vqe-in-a-circuit/9054#9054 - 量子コンピュータで量子化学計算
https://qiita.com/YuichiroMinato/items/8e55e11dabc2cee5f52c
#準備
###Pauli行列と単位行列
$\sigma_{x,y,z}$: Pauli行列,
$I$: 2×2の単位行列
$O$: 2×2のゼロ行列
https://ja.wikipedia.org/wiki/パウリ行列
###X0, X1の行列表現
$\otimes$ : テンソル積( http://enakai00.hatenablog.com/entry/2018/06/03/165815 )
リンク先の「フラットな積」を使って計算を行う．
X_0 = \sigma_x \otimes I = \begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix} \otimes
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
= \begin{pmatrix}
O & I \\
I & O
\end{pmatrix}
= \begin{pmatrix}
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0
\end{pmatrix}
X_1 = I \otimes \sigma_x = \begin{pmatrix}
\sigma_x & O \\
O & \sigma_x
\end{pmatrix}
$Y, Z$に関しても $\sigma_x \rightarrow \sigma_{y,z}$ に置き換えれば良い．
#Coupled-Cluster
Wikipedia: https://ja.wikipedia.org/wiki/%E7%B5%90%E5%90%88%E3%82%AF%E3%83%A9%E3%82%B9%E3%82%BF%E3%83%BC%E6%B3%95
#Unitary Coupled-Cluster (UCC) 法
Variational Quantum Eigensolver (VQE) [参考: https://qiita.com/YuichiroMinato/items/62444351b712743d83b7] の計算を行う際に，初期状態 (ansatz) を準備する．
その一例としてUCC ansatzが用いられている．
簡単な例として$ T(\theta) = \theta a_0^{\dagger}a_1 $を考える．
UCC ansatzの定義に従うと，
$$\begin{align*}
U(\theta) &= \exp[ \theta(a_0^{\dagger}a_1 - a_1^{\dagger}a_0) ] ;. \
&= \exp[ i(\theta/2) (X_0Y_1 - X_1Y_0) ]
\end{align*}
$$
とかける．ここでジョルダンーウィグナー ( Jordan-Wigner ) 変換を用いた．
U(θ)を回路で
$\exp[i(θ/2)Z_0Z_1]$を回路で表してから，それを使って$\exp[ i(\theta/2) (X_0Y_1 - X_1Y_0) ]$を示す．
exp[i(θ/2)Z0Z1]
回路は以下のようにかける
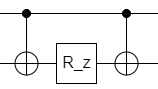
これは回路を行列表現して書き下すと，$\exp[i(θ/2)Z_0Z_1]$と一致していることがわかる．
###補足
回路の演算子は以下の行列でかける．回路は以下の行列の掛け算である。
Controlled NOT gate
\rm{C}_{\rm{NOT}} = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{pmatrix}
$R_z$のgate
I \otimes R_z(\theta) = \begin{pmatrix}
e^{-i\theta/2} & 0 & 0 & 0 \\
0 & e^{i\theta/2} & 0 & 0 \\
0 & 0 & e^{-i\theta/2} & 0 \\
0 & 0 & 0 & e^{i\theta/2}
\end{pmatrix}
ここで1-qubit系の$R_z$はここを参照( https://qiita.com/skiing_LAL10/items/a9ededf64a3991bee191 )
exp[ i(θ/2) (X0Y1 - X1Y0) ]
次に，$\exp[ i(\theta/2) (X_0Y_1 - X_1Y_0) ]$の変換を回路で実現したい．
回転行列を使うと，$R_y(-\pi/2)$はX軸回転からZ軸回転に変更，$R_x(\pi/2)$はY軸回転からZ軸回転に変更できる．
つまり$\exp[ i(θ/2) (X_0Y_1 ) ]$は，上記の$\exp[i(θ/2)Z_0Z_1]$の回路に対し，
1-qubit目に$R_y(-\pi/2)$と$R_y(\pi/2)$を挟み，
2-qubit目に$R_x(\pi/2)$と$R_y(-\pi/2)$を挟めば良い．
同様に，$\exp[ -i(θ/2) (X_1Y_0 ) ]$も作れる．
結局，$\exp[ i(\theta/2) (X_0Y_1 - X_1Y_0) ]$は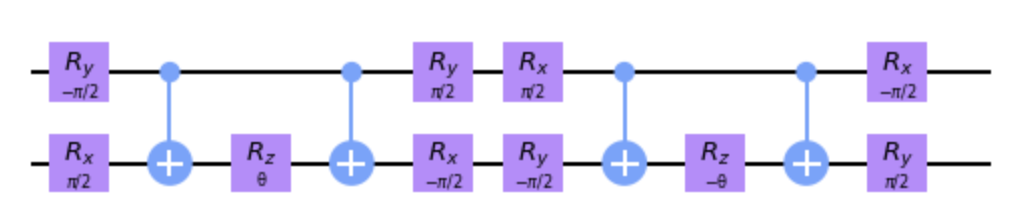
とかける．
#別の表記
$\exp[ i(\theta/2) (X_0Y_1 - X_1Y_0) ]$の演算子は結局，$|00\rangle$から$\cos(\theta/2)|00\rangle + \sin(\theta/2)|11>$を作る演算子である．つまり
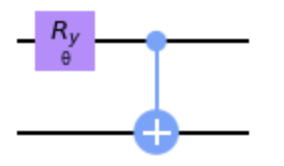
で十分．