$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
TL;DR
- VQEを量子化学計算に用いた場合の、計算精度や必要な計算リソースを見積もったという論文
- VQE(シミュレーション)を用いて、いくつかの分子のエネルギーや化学反応エネルギーを計算した
- 結果、計算精度は古典計算機の手法であるCCSDとCCSD(T)に対し、高精度な順にCCSD(T)>VQE>CCSDとなった
- 同時に、古典計算機で得られている実用的な結果と同程度の計算精度をVQEで得るために必要な計算リソース量(量子ビット数、量子ゲート数)の見積もりを行った
- 結果、上記の精度のために必要な量子ビット数は $100\sim 300$ 個程度、2量子ビットゲート数は $10^5 \sim 10^7$ 個程度であることが推計された
書誌情報
タイトル: Accuracy and Resource Estimations for Quantum Chemistry on a Near-term Quantum Computer
著者&所属:Michael Kühn, Sebastian Zanker, Peter Deglmann, Michael Marthaler, Horst Weiß (BASF SE / HQS Quantum Simulations)
arXiv投稿日:17 Dec 2018
論文リンク:https://arxiv.org/abs/1812.06814
用語の整理
量子化学計算に出てくる用語を軽くまとめます。
初めて読む際には読み飛ばして頂き、本文中で出てきた際にご参照ください。
より詳しい説明は、例えば Quantum computational chemistry をご覧ください。
古典計算手法
Hartree-Fock (HF) 法
多電子系の状態を一つのスレーター行列式状態に制限し、変分法的に解く方法。電子間の相互作用は平均場でしか考慮されていない。近年はpost-HFと呼ばれる、平均場の枠組みを超える近似手法が提案されている。
配置間相互作用(configuration interaction, CI)法
post-HFの一つ。詳しい説明は省くが、HFからスタートして、1電子励起状態、2電子励起状態、...、を考慮して計算する方法。
全ての可能な励起パターンを考える場合は**Full-CI(FCI)**と呼ばれており、(基底関数系が完全な場合に)シュレディンガー方程式を厳密に解く場合と一致するが、分子軌道や電子の数に対して指数関数的に計算量が増大する。
結合クラスター(coupled cluster, CC)法
こちらもpost-HFの一つで、本論文で用いられるUCCSD-VQEのもととなる手法。
CC法ではクラスター演算子と呼ばれる演算子
$$T = \sum_i T_i,$$
$$
T_1 = \sum_{i \in virt, \alpha \in occ} t_{i \alpha} a^\dagger_i a_\alpha,
$$
$$
T_2 = \sum_{i, j \in virt, \alpha, \beta \in occ} t_{i j \alpha \beta} a^\dagger_i a^\dagger_j a_\alpha a_\beta,
$$
$$
...
$$
(ここで、$T_1, T_2,\ldots$はそれぞれ1電子励起、2電子励起、…に対応しており、summationの$occ$ ($virt$)はHartree-Fock状態の内、占有(非占有)軌道を表す)
を用いて
$$
\ket{\psi_\mathrm{CC}} = e^{T} \ket{\psi_\mathrm{HF} }
$$
として基底状態を探索する。ここで$\ket{\psi_\mathrm{HF}}$ は平均場(HF法)で得られる基底状態である。
クラスター演算子$T$に含まれているパラメータ$\{t_{i\alpha}\}$, $\{t_{ij\alpha\beta}\}$, ...が変分パラメータである。
一般に上式の$e^T$はユニタリでないことに注意。
何電子励起までで打ち切るかによっていくつかのパターンがある:
- 2電子励起まで: CCSD (coupled cluster singles/doubles)
- 3電子励起まで: CCSDT (coupled cluster singles/doubles/triples)
- 2電子励起+3電子励起を摂動的に入れる: CCSD(T) (coupled cluster singles/doubles/(triples))
CCSD, CCSD(T)は軌道の数に応じてそれぞれ$N^6, N^7$のオーダーで計算量が増加する。
よって、指数関数的に増加するFCIと比べ、古典計算機でfeasibleとなっている。
密度汎関数法(density functional theory, DFT)
多電子の波動関数を電子密度関数に置き換えてエネルギーを計算する手法。
計算が難しい部分は「交換相関汎関数」に押し付けられており、この交換相関汎関数にどのような近似手法を用いるかでいくつかバリエーションがある(BP86等)。
DFTは一般に$N^3$のオーダーで計算量が増加するため、上記のCC法と比べてはるかに計算が軽い。
なおHartree-Fock法も計算量は$N^3$のオーダーである。
基底関数系
STO-nG
スレーター軌道(STO)を、$n$個のガウス関数の線形和で近似したもの。
ガウス関数を用いることで、重なり積分等の計算が楽になる。
本論文では、STO-3G ( $n=3$ ) がminimal basis set(各電子を表せる最低限の数の軌道)として用いられている。
cc-pVXZ
「correlation-consistent basis sets of valence X-tuple-ζ quality」のことで、上記STOに対し、相関エネルギーを考慮するため、非占有軌道(virtual orbital)も考慮したものである。
XにはD(double), T(triple), Q(Quadruple), 5(quintuple),...が入る。
Xが大きくなるごとに軌道数が増え、一般に近似の精度は上がるが計算は重くなる。
上記のCCSD(T)と基底関数系cc-pV5Zを組み合わせたものは、古典計算化学において"gold standard"(評価の精度が高いものとして広く容認された手法)とされており、本論文でも他手法との比較のための基準として用いられている。
手法
UCCSD-VQE
本論文では上記のCCSDをVQEで実装できる形にしたUCCSD-VQE (unitary coupled-cluster singles/doubles VQE)が用いられている。
ここで通常のCCSDとの違いは、
$$
\ket{\psi_\mathrm{UCC}} = e^{T-T^\dagger} \ket{\psi_\mathrm{HF} }
$$
という部分である。指数の肩を$T$の代わりに$T-T^\dagger$とすることで、指数関数部分がユニタリ変換となり、量子回路で実現することができる。
あとはTrotter展開やJordan-Wigner変換を用いて実装している。
変分パラメータ$\{t_{i\alpha}\}$, $\{t_{ij\alpha\beta}\}$を最適化する手続きは変わらない。
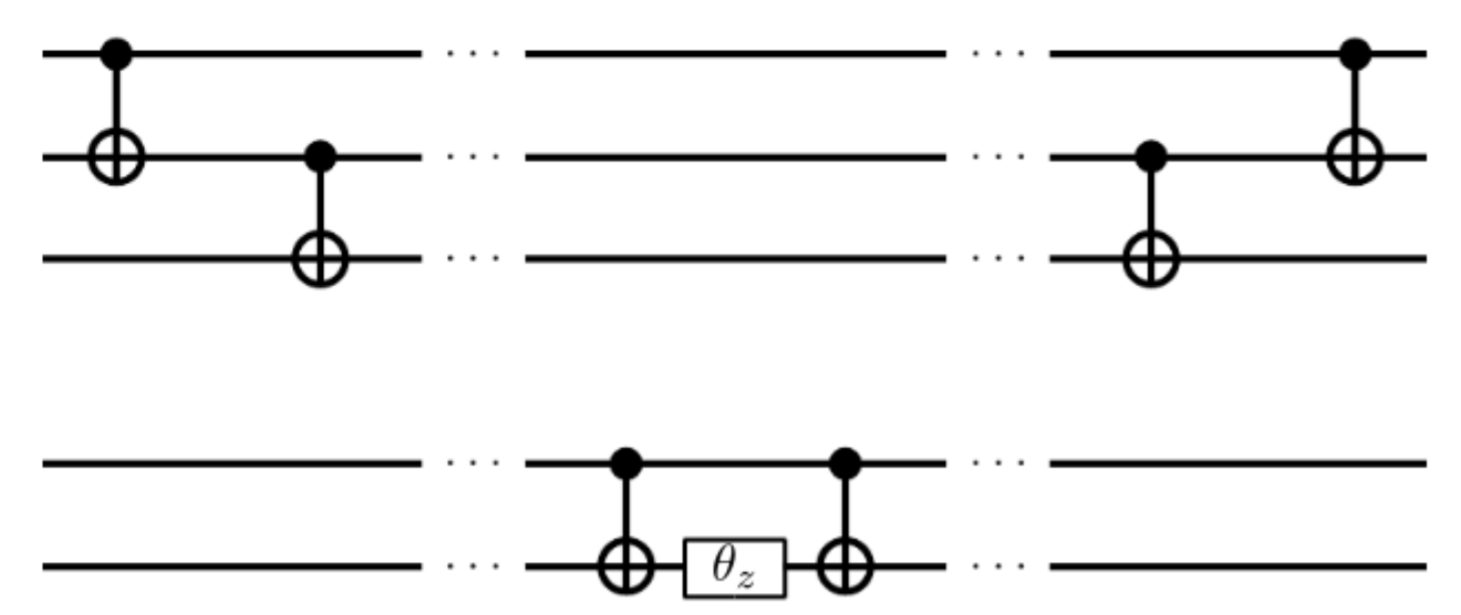
$\ket{\psi_\mathrm{UCC}} $ は Fig.1のような量子回路を用いて得られる (ここで図中の$\theta_z$は、$z$軸に関する$\theta$回転(i.e., $R_z(\theta)=e^{-i\theta\sigma_z/2}$)を表す)。
なお本論文では最適化にscipy.optimizeを用いている。
本論文全体を通して、ノイズの影響は考慮していないことに注意が必要である。
計算コスト削減手法
計算コスト(量子ゲート数)削減のため、以下の手法が用いられている。
MP2 pre-screening
クラスター演算子$T$のパラメータ$\{t\}$の初期値を摂動論(Møller-Plesset摂動理論(2次))で求め、閾値より小さいものは初めからゼロと固定して変分する。
Gate cancellations
量子ゲートの順番を変えることで、$\rm CNOT , CNOT = {\bf 1}$ の性質を利用しゲート数を削減する。
分子のエネルギー計算
単純な構造を持つ分子のいくつか―$\rm{H_2 O}$, $\rm{N_2}$, $\rm{OH}$, $:\rm{CH_2}$(メチレン基のトリプレット状態。2つの不対電子がある)等―について、UCCSD-VQEを用いてエネルギーを計算した。
最小基底の場合
最小基底(minimal basis set)とは、「各電子を表せる最低限の数の軌道」のことで、例えば$\rm{H_2O}$の場合14個の基底関数で構成される(なお$\rm{O}$原子の$\rm{1s}$軌道の"freezing"(他の軌道との混成が無視できること)を考慮すると12軌道となる)。
ここでは各分子について、最小基底としてSTO-3Gを用いてエネルギーを計算している。
本論文で考えている分子についてはSTO-3Gの軌道数はどれも20以下なので、シミュレータを用いて計算できる(スピン・軌道の数が量子ビット数に対応しているので、シミュレータを用いて計算できるのは20軌道程度)。
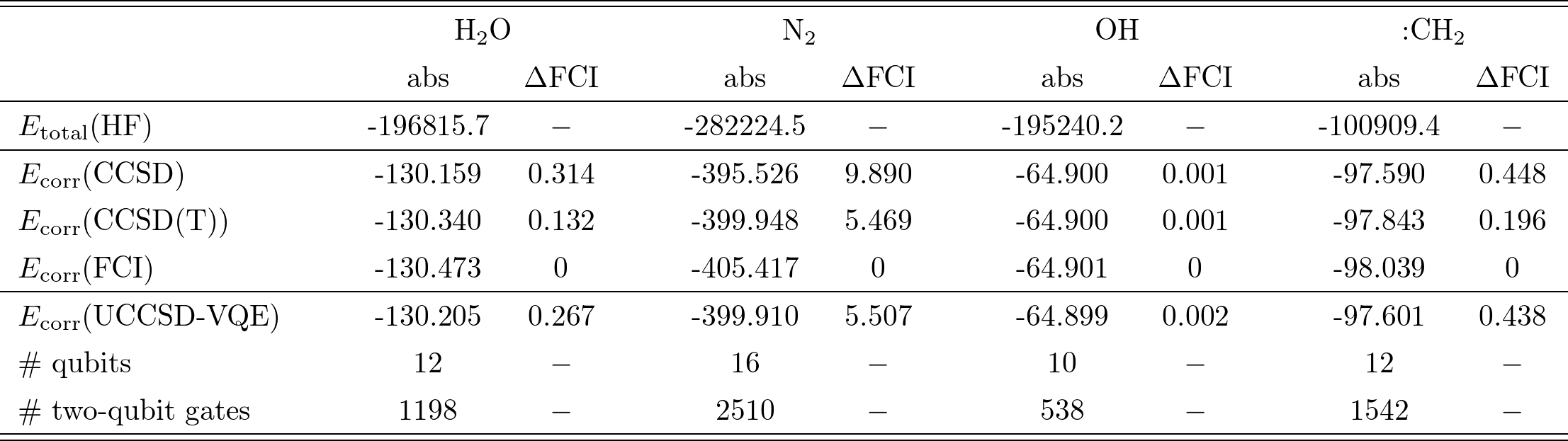
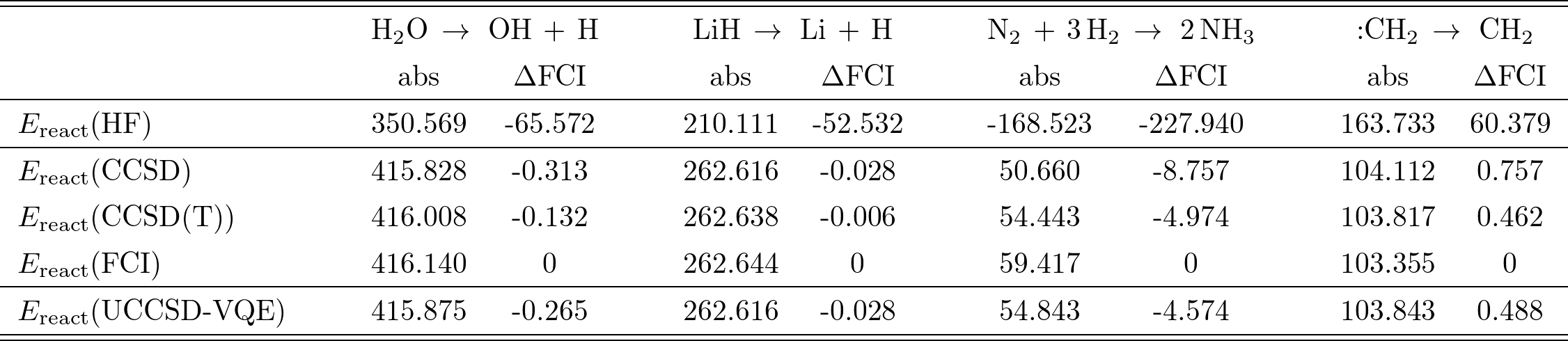
$\rm{H_2 O}$, $\rm{N_2}$, $\rm{OH}$, $:\rm{CH_2}$の4種類の分子についての計算結果はTable I.の通り(単位は全て$\rm{kJ/mol}$)。
各分子について、平均場によるエネルギーと、各近似手法を用いた相関エネルギー、更に(最も厳密に近い手法である)FCIからの誤差「$\Delta \rm{FCI}$」が示されている。
ここで注目すべきは、各分子について、UCCSD-VQEの誤差は、CCSDとCCSD(T)の中間に位置していることである(OHのみCCSDよりも悪いが、これは事実上無視できる値と捉えられている)。
また、Table I.では計算に必要な量子ビット数、2量子ビットゲート数も記載されている。
ここで量子ゲート数は、上記のMP2 pre-screeningやGate cancellationsを適用した上で計算に用いたゲート数である。
より大きな基底関数系へ
古典計算機のシミュレータで扱える量子ビット数には限度があるため、最小基底より大きな基底関数系(cc-pVQZ等)を用いた場合、直接UCCSD-VQEの結果をシミュレートすることはできない。
そこで、前節の経験則「UCCSD-VQEによるエネルギーは、CCSD, CCSD(T)によるエネルギーの中間に位置する」という事実を用いる。
すなわち、より大きな基底関数系の場合にも、CCSD/CCSD(T)による計算結果を、UCCSD-VQEのworst/best caseの推定値とする。
(この手続きを本論文では"extrapolation"と呼んでいる)
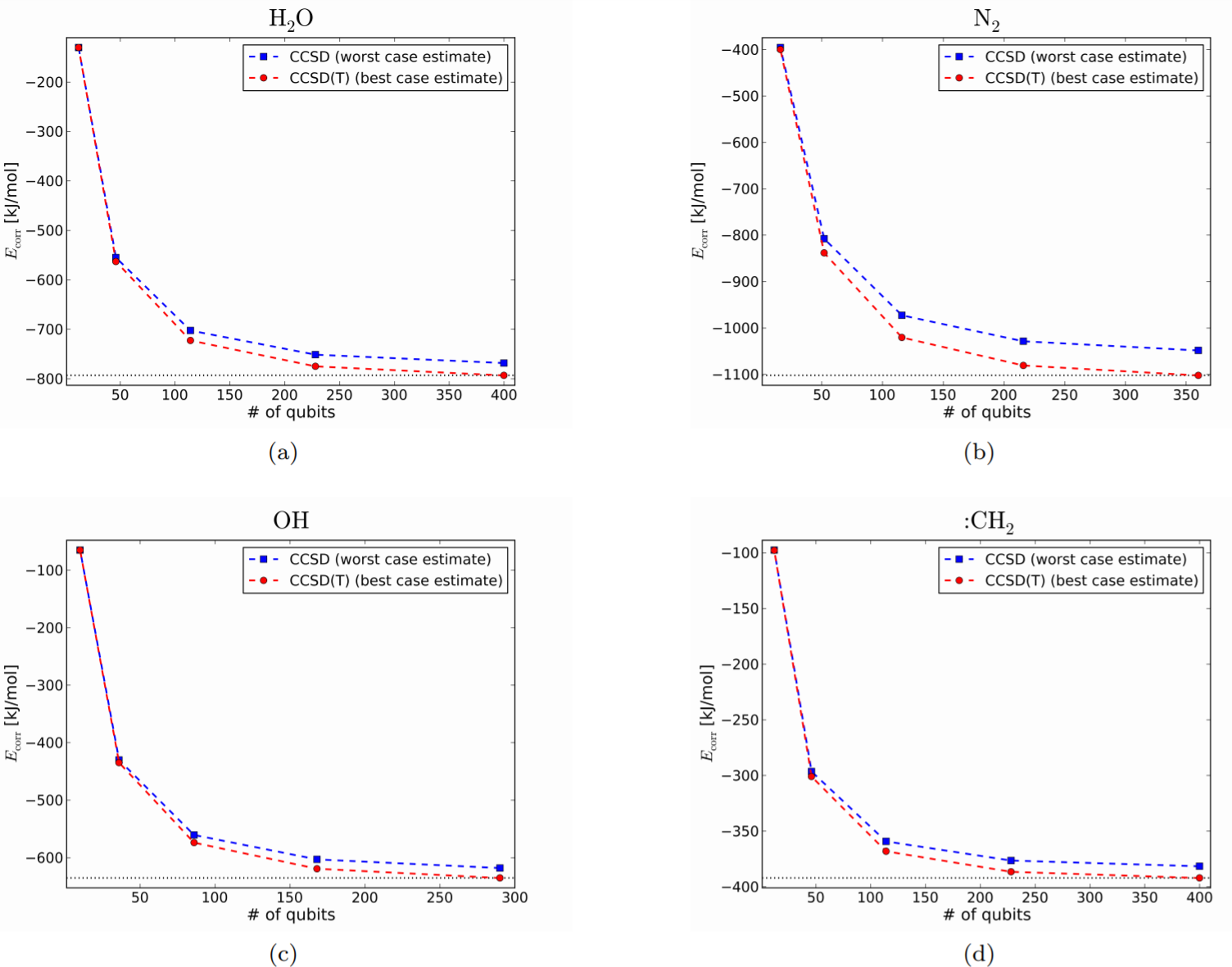
Fig. 6では先程と同じ4つの分子に関して、基底関数を順に大きくしていった場合の、CCSD/CCSD(T)によるエネルギーの計算結果を示している。
ここで、横軸は計算に用いる量子ビット数を表しており、折れ線上の各点は基底関数をSTO-3G, cc-pVDZ, cc-pVTZ, cc-pVQZ, cc-pV5Z と順に増やしていった場合に必要な量子ビット数に対応している。
minimal basis setでの結果から、UCCSD-VQEによるエネルギーの計算値は、Fig.6の赤線と青線の間に来るものと想定される。
また、灰色の線はreferenceである CCSD(T)/cc-pV5Zによるエネルギーを示しており、この値に近ければ高精度な結果が得られていると解釈する。
基底関数を大きくしていくにつれて、精度が上がっている事が見て取れる。
計算精度は、CCSD/CCSD(T)といった手法の選び方よりも、STO-3Gを使うかcc-pVTZを使うかといった基底関数系の選び方によるところが大きいようである。
Fig.6から、(cc-pV5Z のもとで)UCCSD-VQEの上限であるCCSDの値がreference line(灰色の線)に達する(達するの基準は不明瞭)ため、この数(300~400個)の量子ビットを用いれば、UCCSD-VQEの精度は十分良いことがわかる。
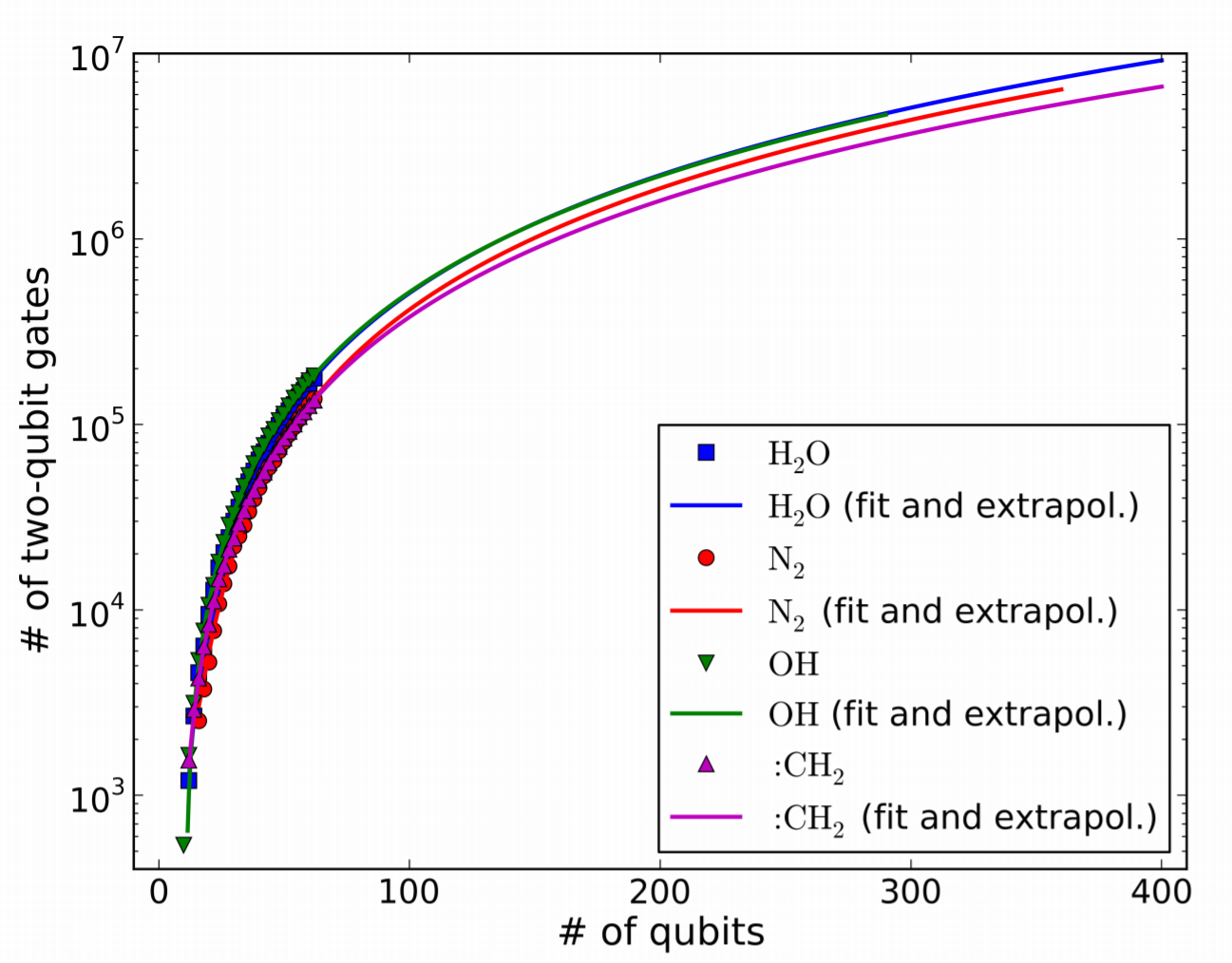
さらに、2量子ビットゲートの必要数について、外挿を用いて見積もったのがFig. 7である。
ここでは64量子ビットまで、必要な2量子ビットゲート数を実際に計算(MP2/gate-cancellation使用)し、それ以上の場合は外挿を行っている。
フィッティングは2次曲線で、殆どの場合決定係数$R^2>0.999$とかなり合っている。
必要な2量子ビットゲート数は、CC演算子の$T_2$振幅の係数$t$の数に比例する。
この$t$の数(パターン数)が、$T_1$に対しては$N_{occ} * N_{virt}$、$T_2$に対しては$N_{occ}^2*N_{virt}^2$に比例することを考えると、必要な2量子ビットゲート数が$N_{virt}$の2次になることは自然と考えられる。
この近似曲線を用いることで、例えば$\rm{H_2O}$でcc-pV5Z(400量子ビット)を用いた場合に必要な2量子ビットゲート数は$9.2 · 10^6$と見積もる事ができる。
以上の結果から、実用に耐える精度にするためには、だいたい以下のリソースが必要である事がわかる。
- $300\sim400$個の量子ビット
- $10^6\sim10^7$個の2量子ビットゲート
しかし、実用上より重要な化学反応エネルギーの計算においては、誤差の"cancellation"が起こることで、より少ない量子ビット/ゲート数で、実用に耐える精度が得られることもある。
化学反応エネルギー
ある化学反応が起こるか否かは、化学反応エネルギー(reaction energy)から決定される。
また、反応エネルギーが分かると、実験で検出可能な量(Gibbs自由エネルギーやエンタルピー、反応レート等)が計算できる。
本節ではハーバー・ボッシュ過程など4種類の化学反応における反応エネルギーを、UCCSD-VQEを用いて計算した。
本節ではCCSD/CCSD(T), FCIに加え、DFTとも比較した。
実用に耐える精度を得るための計算リソースの見積もり等は前節と同じであるが、化学反応エネルギーの計算では、近似による誤差同士の"cancellation"がある。これが精度にどう影響するかが一つの注目すべき点である。
反応エネルギーの計算方法
化学反応エネルギーは、シンプルに
$$ E[反応] = E[生成物] - E[反応物]$$
で与えられる。
例えばハーバー・ボッシュ過程であれば、
$$ E[HB法] = 2E[NH_3] - \{ E[N_2] + 3E[H_2]\}$$
で与えられる。
したがって、計算可能性/計算コストは、反応物・生成物の中で最も計算が難しい物質で決定づけられる。
最小基底の場合
分子のエネルギー計算と同様、STO-3Gを用いてシミュレーションを行った結果がTable IIである。
基底関数系が小さいことから、実験と矛盾している点が多くある(例えばHB法の反応エネルギーが正となっているなど)。
ただし、ここでも前節の分子のエネルギー計算と同様、VQEのFCIからの誤差は、CCSDとCCSD(T)の間に収まっている(HB法を除く。 HB法の場合はcompensationによって誤差が小さくなっている)。
より大きな基底関数系へ
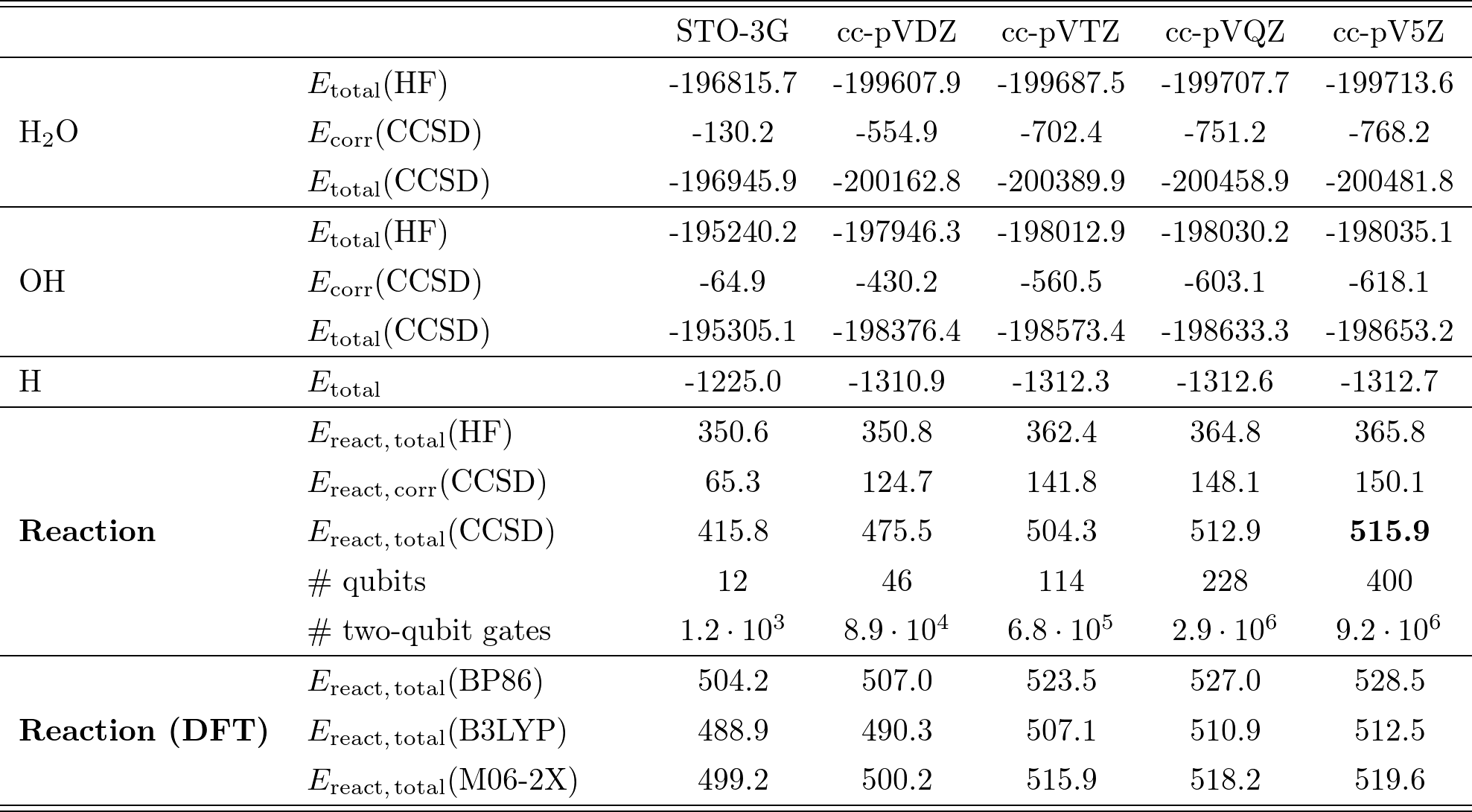
先ほどと同様に、UCCSD-VQEの計算結果をCCSD/CCSD(T)で推計したものがTable III である。
ここでは水分子の解離反応について、様々な基底関数を用いた場合がまとめられている。
Table IIIから、化学反応エネルギーも、基底関数系の種類(cc-pV5Z等)に大きく依存している事がわかる。
ここで、一つ用語の紹介をする。
「chemical accuracy」
化学反応エネルギーの誤差が、$4{\rm kJ/mol (\sim 1kcal/mol)}$ 以内であること。
量子化学において、このchemical accuracyを達成しているかどうかが、その計算手法を評価する基準としてよく用いられる。
以降では、CCSD(T) w/ cc-pV5Zを基準として、そこからの誤差がchemical accuracy以下になることを条件に、必要な量子ビット数/2量子ビットゲート数を見積もっている。
Table IIIでは、cc-pVQZから右側が、この精度を達成している。
Fig.8~11では、個々の化学反応に対して、前節と同様に(a)量子ビット数と誤差の関係、(b)量子ビット数と2量子ビットゲート数の関係 についてプロットしている。
例としてFig.8 (水分子の解離反応)を転載する。
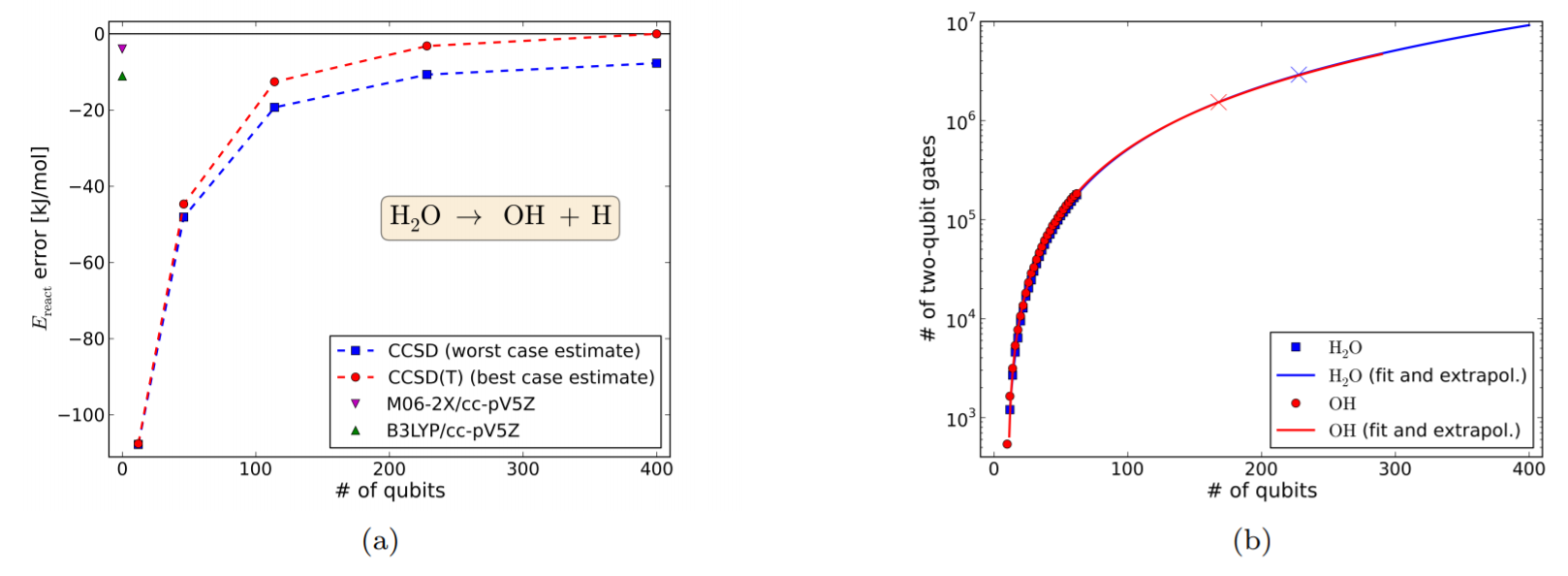
Figure 8.
図の見方は基本的には前節と同じだが、
(b)のXマークは、chemical accuracyを達成するためのリソース量を表している。
結果的に、小さい分子の反応エネルギーのシミュレーションをVQEで行い実用に耐える精度を得るには以下が必要であることが結論付けられている。
- cc-pVQZ or cc-pVTZ
- $100\sim 300$個の量子ビット
- $10^5 \sim 10^7$個の2量子ビットゲート
DFTとの比較
Fig.8(a)の左上の2点は、DFT(交換相関汎関数はM06-2X, B3LYP)を用いた結果であり、一見高精度である。
さらに、DFTはHF法と比べ、計算量としては変わらないことが知られている。
しかし、どの汎関数を使うかによって結果が変化するので、いつでも有効とは言えないことに注意が必要と述べられている。
まとめ
- minimal basis setの場合
- 対象の分子/化学反応では20量子ビット以内なので、古典コンピュータで直接シミュレーションしている(ただし誤差は一切考えていない)
- UCCSD-VQEはCCSDの量子カウンターパートだが、この計算では常にCCSDとCCSD(T)の中間の精度に収まっており、目新しい結果はない
- 必要な量子ビット数は$O(10)$, 2量子ビットゲート数は$O(10^3)$
- より大きなbasis setへ
- 大きなbasis setを用いたVQEに対しては、以下の外挿を行った
- エネルギーはCCSD/CCSD(T)の値を代用
- 量子計算資源の計算は、2次関数で外挿
- UCCSD-VQEを用いた化学反応エネルギーの計算は、cc-pVQZの基底で、$100\sim 300$量子ビット, $10^5 \sim 10^7$個の2量子ビットゲートのもとでchemical accuracy に達することがわかった
- 大きなbasis setを用いたVQEに対しては、以下の外挿を行った
- 同様の外挿手法を用いると、中規模の有機分子に必要な量子ビット数、ゲート数が見積もれる。例えばナフタレン(${\rm C_{10}H_8}$, 68電子)の場合
- cc-pVTZ →$800$, $O(10^7)$
- cc-pVQZ →$1500$, $O(10^8)$
- 実機で計算する場合、ノイズや量子ビットの結合の問題があるので、必要なゲート数はより多くなる可能性がある
VQEは既存の量子化学計算を超えるか?という問いに対して
まとめると、CCSD法に基づくVQE(UCCSD-VQE)だと、量子ビット数$100\sim 300$個、2量子ビットゲート数$10^5\sim10^7$個程度で、やっと既存の手法と並ぶ精度が出ることがわかった。
しかし、その数の量子ビット数をもつ量子コンピュータの登場までにはまだもう少し時間がかかりそうである(現在公開されている量子コンピュータで最高のものではIBMの20量子ビット, 今後実現が予定されているものも含めるとRigettiの128量子ビット)。
また、実際に量子コンピュータを用いる際には、本論文では無視されていたノイズの影響を考えなければならない。現状の2qubitゲートの精度(フィデリティ)は最高でも99.2%程度(参考: https://medium.com/rigetti/engineering-better-2-qubit-gates-e28159862970 )だが、これを$10^5$回も作用させるとなると、全体の精度はかなり悪くなると考えられる。さらに、本論文で見積もられたように、qubit数が2倍, 3倍,...になると、ゲート数はおよそ4倍, 9倍,...になる。したがって、量子コンピュータでより大きな基底系を用いて計算しようとすると、要求される量子ゲート1つあたりの精度も非常に高くなり得る。
このようなノイズの影響を克服し、本論文で用いたものよりbasis-set limitに近い基底関数(cc-pV6Z等)や、より厳密な手法(FCI等)を用いた計算がVQEでより効率的に行えるのであれば、VQEがアドバンテージを持つようになるのかもしれない。
このように、基底状態を求めるのは古典計算がまだまだ有利である一方で、励起状態の計算には、量子計算が有用である可能性がある。
例えば、VQEに一工夫を加えることで励起状態を効率良く計算する手法としてSSVQE (subspace-search variational quantum eigensolver)が提唱されている。
このような量子-古典ハイブリッドアルゴリズムにより、これまで古典計算では難しかった問題が効率的に解けるようになる可能性があるため、今後の発展に期待したい。