この記事は グラフィックス全般 Advent Calendar 2025 11日目の記事です。
作者は個人でElectron&Webなお絵かきアプリを制作中です(9年目)
今回の記事のソースコードはGitHubで公開しています。
背景
2022年の投稿で、4点グラデーショングリッドの試作について紹介したことがあります。マス目一つひとつの描画は今回も同じ処理で描いています。
また、前回の投稿では、Catmull–Clark subdivisionnによるメッシュの細分割を行い、より滑らかなグラデーションを試作しました。
今回は、また別のアプローチで滑らかなグラデーションを行う方法を試したもののご紹介です。
ベジエ補間による細分割
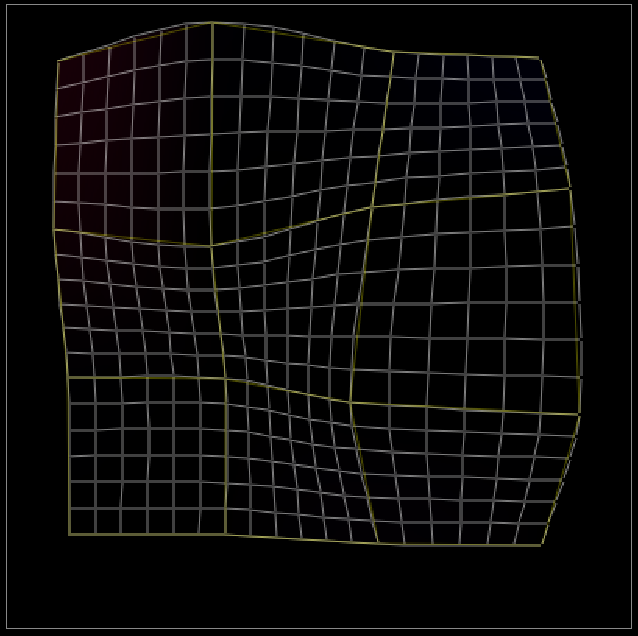
ちょっと分かりづらいのですが、下の図では黄色い線が細分割前のグリッドで、白い線が細分割後のグリッドです。
やっていることは理屈としては単純で、まず黄色い線のうち縦方向の線をベジエ補間で細分割し、次に分割後の頂点ごとに横方向にベジエ補間で細分割しています。
色の補間
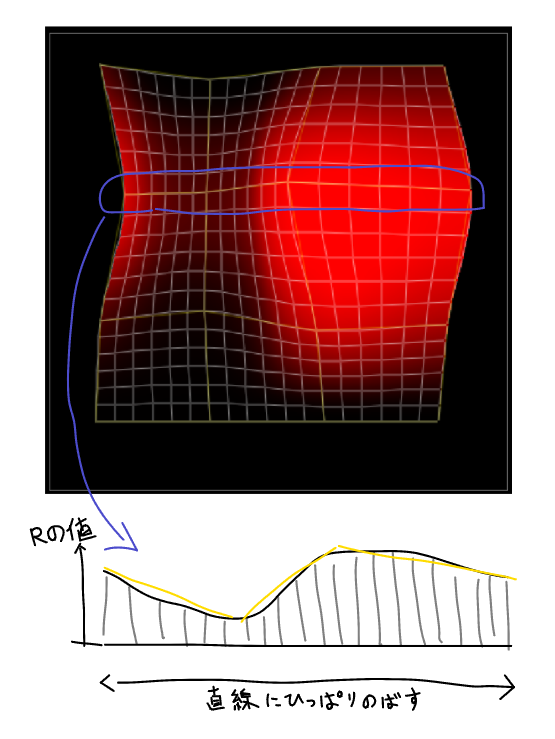
すこし特殊かもしれないのは色の補間です。細分割後のグリッドの縦横の線の長さは、線形補間の場合よりも長さが長くなることが多いです。セルのサイズも等間隔になりません。そのため、単純に線形補間すると、セルが小さいところにギュっと集まった感じで補間されてしまいます。
そこで、縦横の線ごとに線の端から端までの長さを計算し、その長さの中で再分割後の頂点がどのくらいの位置にあるのかを基準に色を補間します。曲線を引っ張り伸ばして横軸にし、色の値を縦軸にして座標系として、その座標系でベジエ補間をする感じです。(説明が難しい…
動くデモ
See the Pen Canvas2D グラデーションベジエグリッドの試作 by 柏崎ワロタロ (@warotarock) on CodePen.
おわりに
今回の試作は、Catmull–Clarknの方法よりも頂点ごとの属性を保持したまま処理しやすいという利点があります。お絵描きアプリでは頂点に複数のパレット色を登録したりもする関係もあり、アプリでは今回の方法を採用することにしました。
任意のメッシュを扱うことができるCatmull–Clarknの方法も何かに使えるはずです。細分割の方法には他にも色リオありますので、特性に合わせて使い分けられたら良さそうですね。