前回投稿の続きです
今回はコンテクスチュアル多腕バンディット問題(Contextual Multi-Armed Bandit)についての簡単な解説と、A/Bテストに対する実装コードを紹介したいと思います。多腕バンディット問題って何? A/Bテストをする際に、データを収集しつつも最終的な成果(報酬)を最大化するような方法が簡単に実装できるの?? などと気になる方は、以下の記事をご覧ください!
(本記事の2章もかなりわかりやすいと思います→ 2.A/Bテストとバンディット問題の理解への導入)
前回投稿: A/Bテストを多腕バンディット問題として解く方法(実装コード付き)
(2024/11/27 追記:LinUCB法を実装して解いてみました(Vol.2))
目次
1.はじめに
2.A/Bテストとバンディット問題の理解への導入 ← おすすめです
3.多腕バンディット問題とは
4.コンテクスチュアル多腕バンディット問題とは
5.実装したソースコードと結果
6.現在の課題と今後の展望について
1. はじめに
この記事並びに以前の投稿記事は、A/Bテストを導入したい、A/Bテストを効率よく行いたい、または多腕バンディット問題の基礎知識を学びたい方向けです(ゴリゴリの理論ではないです、ご容赦ください)。A/Bテストやバンディット問題に対する疑問解決の一端を担うことができれば幸いです。
2. バンディット問題の理解への導入
本章ではA/Bテストとは何かの説明を行います。その後、1つの問題を通して(A/Bテストとバンディット問題に共通する)重要なトレードオフについて解説をします。
A/Bテストとは、最終的な成果(報酬)を最大化するために、複数の候補から最も良い候補を特定する手法です。細かく言うと、複数の候補の中からどんな候補を逐次的に選ぶべきかを求める問題です。ここにおいて候補とは例えば広告です。複数の広告から最もクリック率が高いものを特定して、最終的な総クリック数を最大化すると考えても良いです。また、他には例えば候補とは、WEBページの構成や色合いとしても良いです。
以下の広告のA/Bテストについて考えて見ましょう
あなたはマーケティング責任者として、自社のスーパーセールをインターネットに掲載する予定です。今あなたの目の前には4つの広告候補があります。10000回分の広告掲載で、最終的なクリック数(自社サイトへの遷移数)を最大化するためにどのような考えをしますか?
上のおっちゃんのように、平等に同じ試行回数を重ねて、最終的に一番良い候補をその後ずっと採用し続ければいいじゃん!と思った方も多いかと思います。今回は広告を例に挙げ、
「複数の広告を同じ試行回数ずつ掲載してみて、最終的に一番良いクリック率が高い広告をその後ずっと採用し続ける」
という手法を、以後オッチャン理論と呼びます。
良さそうに思えるオッチャン理論にはいくつかマイナスな側面があります。
1.めっちゃ悪い広告も回数を重ねないといけない
2.(本当は一番良いわけではないといけないのに)試行段階では、クリック率が上振れてしまって、それを今後ずっと採用してしまう可能性がある
3.時間帯やユーザによって、広告それぞれの平均クリック率は変わってしまうと言う点を考慮できていない
4.何回ずつ試してみるかという回数の調整がめっちゃ難しい(最適な回数はそもそもわからない、多すぎも少なすぎも良くない)
このような問題点がオッチャン理論にはありますが、皆さんはどのように考えますでしょうか?
- 1つの広告候補あたり2500回ずつ平等に動かす
- 「広告をランダムに1つ選択して掲載してみる。その広告をクリックしてもらえたら再びその広告を掲載する、クリックしてもらえなかったら、次は別の広告をランダムに掲載する」 を繰り返す
- 1つの広告候補あたり250回ずつ掲載してみて、クリック数(クリック率)が最も高い広告を以後9000回掲載する(オッチャン理論)
このように、良さそうな方法が思い浮かびそうですが、それと同時にどれも最適ではなさそうに思えます。この問題で難しいのは、一番良い広告を見つけながらも、最終的な総クリック数を最大化したいというトレードオフです。ちなみにですが、ここで挙げた例そのものが多腕バンディット問題のインスタンスです。
一番良い広告が知りたい気持ち(探索)と、一番良い(今の所良さそうな)広告をたくさん掲載したい気持ち(活用)がトレードオフになるんですね!!
このジレンマを、exploration-exploitation trade-offと呼びます
3. 多腕バンディット問題とは
多腕バンディット問題とは、最終的な報酬(なんらかの評価)の最大化を目的として、複数の選択肢の中からどんな選択肢を逐次的に選ぶべきかを求める問題です。 最終的な報酬を最大化する という目的が強化学習と同じ点であり、強化学習という分類に属する問題です。
一番良い広告の探索に回数を重ねるほど、一番良い広告を動かすことのできる回数は減ってしまいます。一方で、少ない試行回数で一番良い広告を決めつけてしまうのも要注意です。実際は一番良い広告ではなかったという確率が上がってしまいます。多腕バンディット問題はこのようなトレードオフを含んだ少々複雑な問題です。先ほどは広告の例をしましたが、多くの現実的な問題として考えることができます。
その中の1つとして例えば、
- 治療法の評価において、最も有用な治療法を迅速に特定したい(特定するためには何万人、何十万人という膨大な試行回数を重ねれば特定できるが、コストがかかってしまう。それ以上に 最も有用な治療法ではない治療法を受ける患者数を最小にしたい... )
と言う問題が挙げられます。"Aがいいかな? Bがいいかな? それともパターンCがいいかな?" などと一番良い種類を特定するためのテストを、A/Bテストと呼びます。この多腕バンディット問題に対する方法(手法)は、昔から研究し続けられています。多腕バンディット問題に対する方法(手法)を知りたい方は以下の記事をご覧ください。
A/Bテストを多腕バンディット問題として解く方法(実装コード付き)
4. コンテクスチュアル多腕バンディット問題とは
候補それぞれの特徴や、候補を選択する側(ユーザー側)の特徴を用いて逐次的にどんな候補を選ぶべきかを求める問題です。文脈付き多腕バンディット問題とも呼ばれ、こちらの問題の方がいわゆる現実問題に近しい印象があります。現実的に、ユーザの趣味や年齢、性別といった特徴によって、広告それぞれに対する印象は大きく変わります(何を広告するかによっても同様に変わる)。例えば、英語&&オレンジ色の背景のかっこいい一番右の広告を見ると、少年はウキウキするため、クリック率は高い傾向にあるなどは現実的にありうることです。
今回の実装では、以下の二つの手法を比較したいと思います。そして、A/Bテストをコンテクスチュアル多腕バンディット問題として解くことで、有益であることを示したいと思います。
- ユーザの特徴を踏まえず、ε-greedy法を使用する
- ユーザの特徴を踏まえて、ε-greedy法を使用する
今回のユーザの特徴を踏まえてε-greedy法を使用するという手法は、簡単すぎる手法(厳密に言うと、リグレットの大きさに関する理論的な保証が無い手法)です。しっかりとした優秀な手法については後日記事を書こうと思います。気になる方は、LinUCB方策などと検索してください。
ε-greedy法
- 1-εの確率で、今のところ最も良い(最も期待値の高い、あるいは...率が高い)選択肢を選ぶ
- 今のところ最も良い→ 実際に探索する中で得られた値ですので、暫定的に最良な選択肢と言って良いです。真の値が最も良いかは定かではありません。
- εの確率で、全選択肢の中から平等に選ぶ(選択肢が選ばれる確率は ε/K K:選択肢の個数)
5. 実装したソースコードと結果
今回は4つの広告文の候補に関するA/Bテストを行いました。ユーザの特徴は性別の一点のみとして、それぞれ真のクリック率が以下のようであるとして、10000人に送信してクリック数を比較して見たいとおもいます。4つの広告文を単純に同じくらい送信すると、クリック数は3000件程度になりますが、果たしてどうなるのでしょうか。
以下が実装コードです↓
import numpy as np
import matplotlib.pyplot as plt
# 広告のクリック率(仮に既知の値を設定します)
# このクリック率は、真の値であるので、どちらの場合でも使います
true_acceptance_rates = np.array([
[0.10, 0.25, 0.35,0.50],
[0.50, 0.35, 0.25,0.10],
])
true_acceptance_rates_using_context = np.array([
[0.10, 0.25, 0.35,0.50],
[0.50, 0.35, 0.25,0.10],
])
# エージェントのパラメータ
num_trials = 10000 # 試行回数
epsilon = 0.1 # 探索率 (10%の確率でランダムに選択)
# 各アームの成功数と試行回数のカウンタ
success_counts = [0, 0, 0, 0]
total_counts = [0, 0, 0, 0]
success_counts_using_context = np.array([
[0, 0, 0, 0],
[0, 0, 0, 0],
])
total_counts_using_context = np.array([
[0, 0, 0, 0],
[0, 0, 0, 0],
])
# 各アームの平均クリック率を格納するリスト
average_acceptance_rates = np.array([0, 0, 0, 0], dtype=float)
average_acceptance_rates_using_context = np.array([
[0, 0, 0, 0],
[0, 0, 0, 0],
], dtype=float)
# 全アームに関する平均クリック率
total_average_acceptance_rates = []
total_average_acceptance_rates_using_context = []
# 広告文の選択と報酬の更新
for _ in range(num_trials):
######### Epsilon-Greedyによるアームの選択 ############
user_gender = np.random.randint(0,2) #ランダムに性別を選択、共通です
if np.random.rand() < epsilon:
chosen_arm = np.random.randint(0, 4) # ランダムに選択
else:
chosen_arm = np.argmax(average_acceptance_rates) # 現在の平均クリック率が最大のアームを選択
# 実際のクリック結果をシミュレーション(確率に基づき、クリック/非クリックをランダム決定)
acceptance = np.random.rand() < true_acceptance_rates[user_gender][chosen_arm]
######### Epsilon-Greedyによるアームの選択 ############
if np.random.rand() < epsilon:
chosen_arm_using_context = np.random.randint(0, 4) # ランダムに選択
else:
chosen_arm_using_context = np.argmax(average_acceptance_rates_using_context[user_gender]) # 現在の平均クリック率が最大のアームを選択
# 実際のクリック結果をシミュレーション(確率に基づき、クリック/非クリックをランダム決定)
acceptance_using_context = np.random.rand() < true_acceptance_rates_using_context[user_gender][chosen_arm_using_context]
# 成功数と試行数の更新
success_counts[chosen_arm] += int(acceptance)
total_counts[chosen_arm] += 1
success_counts_using_context[user_gender][chosen_arm_using_context] += int(acceptance_using_context)
total_counts_using_context[user_gender][chosen_arm_using_context] += 1
# 平均クリック率の更新
average_acceptance_rates[chosen_arm] = success_counts[chosen_arm] / total_counts[chosen_arm]
average_acceptance_rates_using_context[user_gender][chosen_arm_using_context] = success_counts_using_context[user_gender][chosen_arm_using_context] / total_counts_using_context[user_gender][chosen_arm_using_context]
total_average_acceptance_rates.append(sum(success_counts) / sum(total_counts))
total_average_acceptance_rates_using_context.append(sum(map(sum,success_counts_using_context)) / sum(map(sum,total_counts_using_context)))
# 結果の表示
# for i in range(4):
# print(f"広告文 {i + 1}:")
# print(f" - 実際のクリック率: {true_acceptance_rates[i]:.2f}")
# print(f" - 推定クリック率: {average_acceptance_rates[i]:.2f}")
# print(f" - 試行回数: {total_counts[i]}")
print(f"\n広告全体の合計クリック数: {sum(success_counts)}")
print(f"\n{average_acceptance_rates}")
print(f"\n広告全体の合計クリック数(文脈付き): {sum(map(sum,success_counts_using_context))}")
print(f"\n{average_acceptance_rates_using_context}")
# グラフを描画
plt.plot(np.arange(10000), total_average_acceptance_rates, label=f"ε-greedy ε={epsilon}")
plt.plot(np.arange(10000), total_average_acceptance_rates_using_context, label=f"ε-greedy_using_context ε={epsilon}")
plt.xlabel("Trials")
plt.ylabel("Acceptance Rate")
plt.title("Average Acceptance Rate Over Time")
plt.legend()
plt.grid()
plt.savefig(f'Average_Acceptance_Rate_using_context_1_ε={epsilon}.png') # PNG形式で保存
plt.show()
結果1 ε = 0.2

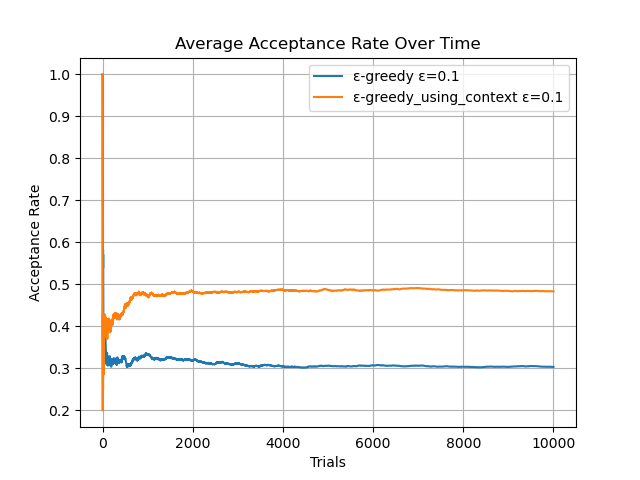
結果2 ε = 0.1
結果3 ε = 0.05

結果4 ε = 0.01

4つの結果どれにおいても、文脈を使うこと方が最終的なクリック率が高いことがわかりました。今回のこの環境においては、クリック率の最大の期待値は0.5です。最終的なクリック率を見ると、40-47%あたりに収束していることがわかるかと思います。文脈を使わないよりは良いことは目に見えてわかりますが、ε=0.05の場合、確率の上昇が収束するまでに3000回程度かかってしまっています。また、ε=0.01に至っては10000回までに確率の収束がされておらず、10000回を通して探索自体に手間がかかっているように思えます。また、ε=0.20の場合、ランダム性が強いままのため、確率の上昇が45%程度で止まってしまっています。
動的にε(イプシロン)の値を変えたいですね....
6. 現在の課題と今後の展望について
今後についてですが、まずはパターン数が膨大になってしまうと言う課題に対処できる工夫について紹介したいと思います。具体的には線形バンディット問題と呼ばれる問題について取り扱おうと思います。
(2024/11/27 追記:LinUCB法を実装して解いてみました(Vol.2))
詳しくてわかりやすい解説記事: https://qiita.com/tsugar/items/b809f8d6399cc988aa69
詳しくてわかりやすい解説記事: https://qiita.com/pocokhc/items/fd133053fa309bdb58e6
詳しくてわかりやすい解説記事: https://qiita.com/usaito/items/ad15394547bd5daf8937



