Vol.1からの続きです
今回はコンテクスチュアル多腕バンディット問題(Contextual Multi-Armed Bandit)についての簡単な解説と、LinUCB法について書きたいと思います。多腕バンディット問題って何? A/Bテストをする際に、データを収集しつつも最終的な成果(報酬)を最大化するような方法が簡単に実装できるの?? などと気になる方は、以下の記事をご覧ください!
(本記事の2章もかなりわかりやすいと思います→2.A/Bテストとバンディット問題の理解への導入)
バンディット問題の投稿: A/Bテストを多腕バンディット問題として解く方法(実装コード付き)
前回の投稿: A/Bテストを コンテクスチュアル多腕バンディット問題として解く方法-Vol.1(実装コード付き)
目次
1.はじめに
2.A/Bテストとバンディット問題の理解への導入 ← おすすめです
3.Vol.1の手法を改善してみよう(LinUCB法解説前の導入)
4.線形回帰とLinUCB法
5.実装したソースコードと結果
6.現在の課題と今後の展望について
1. はじめに
この記事並びに以前の投稿記事は、A/Bテストを導入したい、A/Bテストを効率よく行いたい、または多腕バンディット問題の基礎知識を学びたい方向けです(ゴリゴリの理論ではないです、ご容赦ください)。A/Bテストやバンディット問題に対する疑問解決の一端を担うことができれば幸いです。
2. バンディット問題の理解への導入
本章ではA/Bテストとは何かの説明を行います。その後、1つの問題を通して(A/Bテストとバンディット問題に共通する)重要なトレードオフについて解説をします。
A/Bテストとは、最終的な成果(報酬)を最大化するために、複数の候補から最も良い候補を特定する手法です。厳密に言うと、複数の候補の中からどんな候補を逐次的に選ぶべきかを求める問題です。ここにおいて候補とは例えば広告です。複数の広告から最もクリック率が高いものを特定して、最終的な総クリック数を最大化すると考えても良いです。また、他には例えば候補とは、WEBページの構成や色合いとしても良いです。
以下の広告のA/Bテストについて考えて見ましょう
あなたはマーケティング責任者として、自社のスーパーセールをインターネットに掲載する予定です。今あなたの目の前には4つの広告候補があります。10000回分の広告掲載で、最終的なクリック数(自社サイトへの遷移数)を最大化するためにどのような考えをしますか?
上のおっちゃんのように、平等に同じ試行回数を重ねて、最終的に一番良い候補をその後ずっと採用し続ければいいじゃん!と思った方も多いかと思います。今回は広告を例に挙げ、
「複数の広告を同じ試行回数ずつ掲載してみて、最終的に一番良いクリック率が高い広告をその後ずっと採用し続ける」
という手法を、以後オッチャン理論と呼びます。
良さそうに思えるオッチャン理論にはいくつかマイナスな側面があります。
- めっちゃ悪い広告も回数を重ねないといけない
- (本当は一番良いわけではないといけないのに)試行段階では、クリック率が上振れてしまって、それを今後ずっと採用してしまう可能性がある
- 時間帯やユーザによって、広告それぞれの平均クリック率は変わってしまうと言う点を考慮できていない
- 何回ずつ試してみるかという回数の調整がめっちゃ難しい(最適な回数はそもそもわからない、多すぎも少なすぎも良くない)
このような問題点がオッチャン理論にはありますが、皆さんはどのように考えますでしょうか?
- 1つの広告候補あたり2500回ずつ平等に動かす
- 「広告をランダムに1つ選択して掲載してみる。その広告をクリックしてもらえたら再びその広告を掲載する、クリックしてもらえなかったら、次は別の広告をランダムに掲載する」 を繰り返す
- 1つの広告候補あたり250回ずつ掲載してみて、クリック数(クリック率)が最も高い広告を以後9000回掲載する(オッチャン理論)
このように、良さそうな方法が思い浮かびそうですが、それと同時にどれも最適ではなさそうに思えます。この問題で難しいのは、一番良い広告を見つけながらも、最終的な総クリック数を最大化したいというトレードオフです。ちなみにですが、ここで挙げた例そのものが多腕バンディット問題のインスタンスです。
一番良い広告が知りたい気持ち(探索)と、一番良い(今の所良さそうな)広告をたくさん掲載したい気持ち(活用)がトレードオフになるんですね!!
このジレンマを、exploration-exploitation trade-offと呼びます
3. Vol.1の手法を改善してみよう(LinUCB法解説前の導入)
前回の記事(Vol.1)の6章で、Vol.1で実装した簡単な手法の課題について挙げました(8通りそれぞれで、クリック率を計算して最適な広告を探索する手法)。↓こんな課題がありましたね。
今回はLinUCB法という有名で強力な手法でさらに最終的な報酬を増やしていきましょう。まずは引き続き使用する環境設定についてです。
この環境は 広告の背景の色と文字が2種類ずつの4パターン、ユーザーの性別が2種類というシンプルな設定になっています。広告4は男性に大好評で、広告1は女性に大好評といったところです。ユーザが男性女性かということを考慮しない場合は30%のクリック率となります。合計で8パターンあります。前回は8通りそれぞれでクリック率が逐次的にどのくらいかなというのを計算しました。よって、
- 探索に時間がかかる
- 実際に良い広告が本当に良いという信頼性を上げにくい(全パターンを何回も試行錯誤しないと信頼性が高くならないため)
こう言ったことが課題に挙げられます。
パターン数が膨大になってしまう課題に対するアプローチ
→あるパターンでの情報をもとに、似通ったパターンも推測するというアプローチを取ります。もしかしたらあれ回帰っぽい?と思ったかもしれません。そうです、既知のデータから関係性(モデル)を学習し、未知のデータを予測するという回帰です。回帰の中でも一番シンプルな線形回帰を使って、パターン数が膨大になってしまう課題に対して解決策を見出していきましょう!
4. 線形回帰とLinUCB法
線形回帰とは
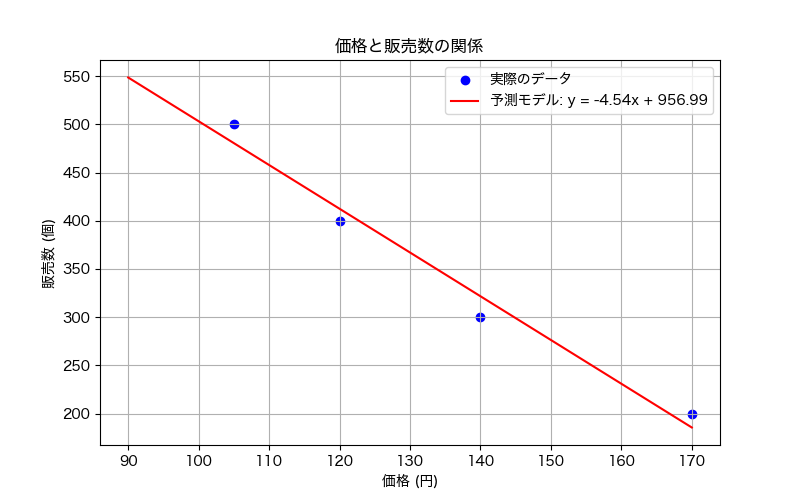
既知のデータから関係性(モデル)を学習し、未知のデータを予測するために使われる手法です。例えば価格と販売数のデータが下のように4つ分かったとします。
今データとしては
- 105円で販売した場合の販売数
- 120円で販売した場合の販売数
- 140円で販売した場合の販売数
- 170円で販売した場合の販売数
の4つしかありません。しかし、なんとなくここから130円で売った場合や200円で売った場合が予測できそうですよね。これを先ほどの広告の場合にも適用することができます。
- (背景が)オレンジっぽいと男性ウケいいのかな??
- (背景が)青っぽいと女性ウケがいいのかな?
- (見出しを)英語で書くと、男性ウケいいのかな?
- (見出しを)日本語で、女性ウケがいいのかな?
1つ1つの条件を見ていくと上のような傾向が見えてきそうです。
LinUCB法とは
LinUCB(Linear Upper Confidence Bound)法とは、コンテクスチュアル多腕バンディット問題を解く用に、UCB法をベースに改良された手法です。UCB法とは、各候補の報酬期待値の信頼区間の上限を比較して、選択していく手法です。具体的には全候補のうち、最も報酬期待値の信頼区間の上限が高い候補を逐次的に選択していくという手法です。
例えば [広告の背景青色, 広告の見出し英語, ユーザー男性] というパターンを無限回行ったら、クリック率は25%に限りなく近くなりますね。クリックしてもらえたら1、してもらえなかったら0とすると、報酬期待値の信頼区間の下限と報酬期待値の信頼区間の上限は両方限りなく0.25に近づきますね。しかし10回しか広告していない場合はどうでしょうか。10回だけで期待値の信頼区間は簡単に狭まりませんね。クリックされるのが1回だけという場合も、5回もという場合も大いにありそうですね。よって、広告回数がまだ少ない場合には、信頼区間の上限がかなり大きい値になります(同様に下限も...かなり小さい値になる)。信頼区間の計算方法については省略しますが、
UCB法の特徴としては2つ以下のことが言えます
- 現時点での広告のクリック率の良し悪しだけでなく、広告回数の少なさを考慮している点(つまり少ないほど、信頼区間の上限が高いため、選択されやすい)
- (広告回数を重ねるほど、信頼区間の上限も真のクリック率に近くなっていくため)ある程度回数を重ねると、現時点での広告のクリック率の良し悪しで評価していく
回数を重ねるごとに徐々に最適そうな候補を絞っていく手法ですね。このために信頼区間の上限値を活用するというのは、画期的な発想だと私は感じました。LinUCBの詳細を知りたい方はこちらの記事を参照してください。
5. 実装したソースコードと結果
今回も4つの広告文の候補に関するA/Bテストを行いました。ユーザの特徴は性別2種類のみとして、それぞれ真のクリック率が以下のようであるとして、10000人に送信してクリック数を比較して見たいとおもいます。4つの広告文を単純に同じくらい送信すると、クリック数は3000件程度になります。また、前回記事のコンテクスチュアルを使ったε-greedy法の結果は下のようになっており、うまくいったときでも4800〜4850程度でした。
(Vol.1の結果はこちら↓)
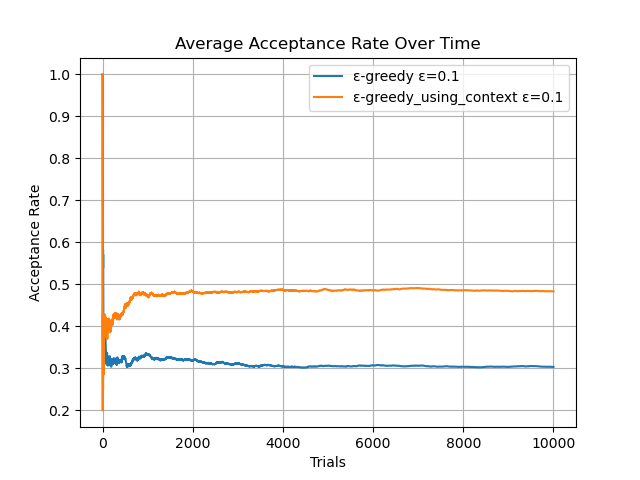
実装に関してはhttps://qiita.com/usaito さん作のpyMABをベースにさせていただきました。具体的には、広告側の文脈(特徴)を組み込めるように変えました。https://qiita.com/usaito/items/e727dcac7325b50d4d4c にCMABについての詳しい解説がございます。
以下が実装コードです↓
実装コード1 (LinUCB法部分以外)
import numpy as np
import PyMAB
from PyMAB.policy import EpsilonGreedy, GaussianThompsonSampling, LinUCB, LinTS, LogisticTS
from PyMAB.policy import LinUCB
# アームの固定特徴量(背景色と文字言語)
# 背景色(オレンジ=1、青=0)、文字言語(日本語=1、英語=0)
arm_features = np.array([
[1.0, 1.0], # オレンジ背景、日本語
[-1.0, 1.0], # 青背景、日本語
[1.0, -1.0], # オレンジ背景、英語
[-1.0, -1.0], # 青背景、英語
])
# 真の報酬行列(性別: 男性=0, 女性=1)
true_rewards = np.array([
[0.10, 0.25, 0.35, 0.50], # 男性
[0.50, 0.35, 0.25, 0.10], # 女性
])
total_average_acceptance_rates_LinUCB = []
# LinUCBの設定
n_arms = arm_features.shape[0]
user_feature_dim = 1 # ユーザーの特徴量次元(性別のみ)
arm_feature_dim = arm_features.shape[1] # アームの特徴量次元
d = user_feature_dim + arm_feature_dim # 総特徴量次元
alpha = 0.5 # 探索パラメータ
# pyMAB の LinUCB インスタンス
print(d)
linucb = LinUCB(n_arms=n_arms, n_features=d, alpha=alpha, warmup=1)
print(linucb.A_inv)
# シミュレーション
n_rounds = 10000
total_reward = 0
select_count_list = np.array([
[0,0,0,0], # 男性
[0,0,0,0], # 女性
])
reward_count_list = np.array([
[0,0,0,0], # 男性
[0,0,0,0], # 女性
])
for t in range(n_rounds):
# ランダムに性別を選択(男性=0, 女性=1)
user_gender = np.random.choice([-1.0, 1])
#user_gender = 0
user_feature = np.array([user_gender]) # ユーザーの特徴量
# 動的に特徴量行列を生成(各アームの特徴量にユーザーの特徴を追加)
# np.tile(a,b) aをb回複製する
# print(user_feature, )
X = np.hstack([arm_features, np.tile(user_feature, (n_arms, 1))])
#print('選択スタート:' )
# アームをLinUCBで選択
chosen_arm = linucb.select_arm(X)
# 報酬を計算(確率的な成功/失敗)
user_gender = 0 if user_gender == -1.0 else 1
reward = np.random.rand() < true_rewards[user_gender, chosen_arm]
#print(f'{chosen_arm+1}番のアームを選択してreward:{reward}, true_rewards:{true_rewards[user_gender, chosen_arm]}')
# LinUCBに報酬を渡して更新
linucb.update(X[chosen_arm], chosen_arm, reward )
select_count_list[user_gender][chosen_arm] +=1
reward_count_list[user_gender][chosen_arm] +=reward
# 累積報酬を更新
total_reward += reward
total_average_acceptance_rates_LinUCB.append(total_reward/(t+1))
print(f"Total reward after {n_rounds} rounds: {total_reward}")
print(linucb.counts)
print(linucb.A_inv)
print(linucb.b)
theta_hat = np.concatenate([linucb.A_inv[i] @ np.expand_dims(linucb.b[:, i], axis=1) for i in np.arange(4)], axis=1)
print(np.concatenate([linucb.A_inv[i] @ np.expand_dims(linucb.b[:, i], axis=1) for i in np.arange(4)], axis=1))
# グラフを描画
plt.plot(np.arange(10000), total_average_acceptance_rates, label=f"ε-greedy ε={epsilon}")
plt.plot(np.arange(10000), total_average_acceptance_rates_using_context, label=f"ε-greedy_using_context ε={epsilon}")
plt.plot(np.arange(10000), total_average_acceptance_rates_LinUCB, label=f"LinUCB alpha={alpha}")
plt.xlabel("Trials")
plt.ylabel("Acceptance Rate")
plt.title("Average Acceptance Rate Over Time")
plt.legend()
plt.grid()
plt.savefig(f'data/Average_Acceptance_Rate_using_context_1_ε={epsilon}_compared_to_LinUCB_alpha={alpha}.png') # PNG形式で保存
plt.show()
pyMABのcontextual.pyを改変↓
実装コード2 (LinUCB法)
class LinUCB(BaseContextualPolicy):
"""Linear Upper Confidence Bound.
Parameters
----------
n_arms: int
The number of given bandit arms.
n_features: int
The dimention of context vectors.
alpha: float, optional(default=1.0)
The hyper-parameter which represents how often the algorithm explores.
warmup: int, optional(default=1)
The minimum number of pull of earch arm.
batch_size: int, optional (default=1)
The number of data given in each batch.
References
-------
[1] L. Li, W. Chu, J. Langford, and E. Schapire.
A contextual-bandit approach to personalized news article recommendation.
In Proceedings of the 19th International Conference on World Wide Web, pp. 661–670. ACM, 2010.
"""
def __init__(self, n_arms: int, n_features: int, alpha: float=1.0, warmup: int=1, batch_size: int=1) -> None:
"""Initialize class."""
super().__init__(n_arms, n_features, warmup, batch_size)
self.alpha = alpha
self.name = f"LinUCB(α={self.alpha})"
self.theta_hat = np.zeros((self.n_features, self.n_arms)) # d * k
self.A_inv = np.concatenate([np.identity(self.n_features)
for i in np.arange(self.n_arms)]).reshape(self.n_arms, self.n_features, self.n_features) # k * d * d
self.b = np.zeros((self.n_features, self.n_arms)) # d * k
self._A_inv = np.concatenate([np.identity(self.n_features)
for i in np.arange(self.n_arms)]).reshape(self.n_arms, self.n_features, self.n_features)
self._b = np.zeros((self.n_features, self.n_arms))
#print("GOOD")
def select_arm(self, x: np.ndarray) -> int:
"""Select arms according to the policy for new data.
Parameters
----------
x : array-like, shape = (n_features, )
A test sample.
Returns
-------
result: int
The selected arm.
"""
# print(f"x shape: {x.shape}")
# print(f"A_inv[i] shape: {self.A_inv.shape}")
if True in (self.counts < self.warmup):
result = np.argmax(np.array(self.counts < self.warmup, dtype=int))
else:
# print(f'x.shape::: {x.shape}')
# #x = _check_x_input(x)
# print(f'x.shape::: {x.shape}\n')
self.theta_hat = np.concatenate([self.A_inv[i] @ np.expand_dims(self.b[:, i], axis=1) for i in np.arange(self.n_arms)], axis=1) # user_dim * n_arms
# sigma_hat = np.concatenate([np.sqrt(x.T @ self.A_inv[i] @ x) for i in np.arange(self.n_arms)], axis=1) # 1 * n_arms
# result = np.argmax(x.T @ self.theta_hat + self.alpha * sigma_hat)
# sigma_hat: 各アームごとに計算
sigma_hat = np.concatenate(
[np.sqrt(x_i.T @ self.A_inv[i] @ x_i).reshape(1,1) for i, x_i in enumerate(x)],
axis=1
)
#print(f'θハットは、{[self.theta_hat[:, i] for i, x_i in enumerate(x)]}です')
# 報酬推定値と信頼区間を加味してアームを選択
#print(f'期待値こんな感じ:{[x_i.T @ self.theta_hat[:, i] for i, x_i in enumerate(x)]}\n')
result = np.argmax([x_i.T @ self.theta_hat[:, i] + self.alpha * sigma_hat[0, i] for i, x_i in enumerate(x)])
# print(f'result: {result}')
return result
def update(self, x: np.matrix, chosen_arm: int, reward: Union[int, float]) -> None:
"""Update the reward and parameter information about earch arm.
Parameters
----------
x : array-like, shape = (n_features, )
A test sample.
chosen_arm: int
The chosen arm.
reward: int, float
The observed reward value from the chosen arm.
"""
#print('アップデータ スタート')
x = _check_x_input(x)
#print(f'x.shape::: {x.shape}')
self.data_size += 1
self.counts[chosen_arm] += 1
self.rewards += reward
tmp = self._A_inv[chosen_arm]
self._A_inv[chosen_arm] -= \
self._A_inv[chosen_arm] @ x @ x.T @ self._A_inv[chosen_arm] / (1 + x.T @ self._A_inv[chosen_arm] @ x) # d * d
#print(f'A_invは{tmp}から{self._A_inv[chosen_arm]}へ更新' )
tmp = self._b
self._b[:, chosen_arm] += np.ravel(x) * reward # d * 1
#print(f'bは\n{tmp}から\n{self._b}へ更新\n' )
if self.data_size % self.batch_size == 0:
self.A_inv, self.b = np.copy(self._A_inv), np.copy(self._b) # d * d, d * 1
実験結果
LinUCB法にはαというパラメータがあります。大きければ大きほど探索をしよう!というランダム性が大きくなるパラメータです。今回の実験では α = 0.1, 0.5, 0.7, 1, 10の5つで実験を行いました。LinUCB法の結果は緑色の線です。




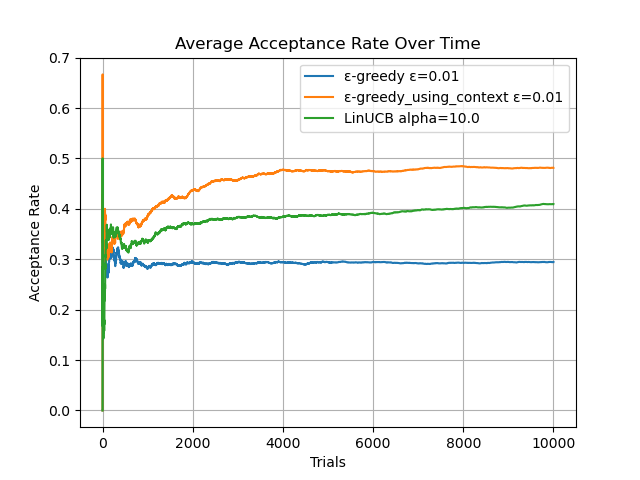
α=0.5における詳細な結果
1. LinUCB法による各広告のクリック率の予測結果
性別:男性の場合に、それぞれの広告のクリック率予測↓矢印
[0.166, 0.0151, 0.2622, 0.5042]
実際の値
[0.10, 0.25, 0.35, 0.50]
2. LinUCB法による、広告選択数の結果(0行目が男性、1行目が女性に対する広告選択数)
array([
[ 6, 2, 15, 4904], <- 男性の場合の選択数
[5021, 31, 19, 2] <- 女性の場合の選択数
])
しっかりと少ない探索回数で最もクリック率の高い広告を選択できていますね!
3. LinUCB法で得られたクリック数
array([
[ 1, 0, 4, 2473], <- 男性の場合のクリック数
[2478, 9, 5, 0] <- 女性の場合のクリック数
])
実際のクリック数もおおよそ確率通りですね。効率よくクリック数を稼げていると言えますね!
考察
α = 0.1, 0.5, 0.7, 1, 10のうち α = 0.5, 0.7, 1 で前回の手法を上回る結果となりました。特に優れた特徴としては0〜2000回部分です。Vol.1手法と比較して探索速度が大幅に高いことがわかります。また、50%を超えるてしまったのは上振れですが、以前として4900/10000程度は高確率で出るという感覚です。α=0.1では探索の気持ちが少なすぎて、0.35のクリック率で満足してしまっています。一方でα=10では探索の気持ちが強すぎて40%程度の結果になってしまいました。
6. 現在の課題と今後の展望について
今後についてですが、いろんな実験結果を紹介できたら良いかなと思います! 特に8パターン→16や32パターンにしたときに、どのくらい性能差があるかの比較は、有益なのかなと思っております。