はじめに
先日, TwitterでArtwork Personalization at Netflixという記事が話題になっていました. 実は, この記事が元になったセッションもRecsys18という推薦システムにおいて世界最大の国際会議で催されていたようです(資料).
この記事の主題は, Netflixが配信しているコンテンツのArtwork(いわゆるサムネ)をユーザーごとに最適化することで, より良いユーザー体験を届けたいというものです. 以下の画像のように一つの作品をとってもたくさんのArtworkの候補が考えられます. その作品の中でどの場面を切り取るかによって, 個々がその作品に興味を抱く度合いは変わってくると思われます. ロマンスが好きな人にはカップルが映るシーンを, コメディが好きな人には有名なコメディアンが映るシーンを用いたArtworkがいいんじゃないかみたいなことです(もちろん現実はもっと複雑).

Artwork Personalization at Netflixより
ここで, Cold-Start と呼ばれるレコメンドでは有名な問題が起こり得ます. この問題は, 新たな作品やユーザーや追加された時に, それらに関する有効なレコメンドが難しいという問題です. このCold-Startは, 毎日多くの新規作品や新規ユーザーが追加されていると考えられるNetflixのケースでも問題になると考えられます. このCold-Start に対する一つの解決策として, バンディットアルゴリズム と呼ばれる技術があります. このアルゴリズムを用いれば最適な選択をできるだけ多く取りたいという活用と最適な選択が何であるかをできるだけ正確に知りたいという探索をバランス良く織り交ぜることができ, 私も以前2つほど記事を書きました. (基本編) (Thompson Sampling)
ただし, これらの記事で紹介したアルゴリズムは最良な選択肢を探索する際にユーザーの特徴量を考慮に入れていませんでした. つまり, 典型的なバンディットアルゴリズムは「これまでにどのArtworkを使って, それぞれ何回視聴されたか」という情報のみから次にどのArtworkを用いるべきかを決めるアルゴリズムでした.
しかし, Netflixの目的の一つには個別化というものがありました. Artwork側だけの情報だけではなくて, ユーザーに関する情報も加味した上で, 各ユーザーに最適なArtwork を探索できるようなアルゴリズムが必要な問題設定となっています. NetflixはこれをContextual Bandit と呼ばれる発展版のアルゴリズムを用いて解決したと書いてあります. Part 1ではこのContextual Banditについて詳しく解説していきます.
目次
- Contextual Banditとは
- LinUCB
- 線形モデル上のThompsonSampling
- ロジスティック回帰とThompsonSampling
- 実験
- Part 2への繋ぎ
- 参考
Contextual Banditとは
「はじめに」で導入しましたが, Contextual Banditは文脈(ユーザーの特徴など, context)に応じて各アーム(選択肢のこと, 今回はArtworkの選択肢)の報酬構造が変化すると考えます. 正確に言うと, 事前にアームの報酬に対して仮定した確率分布のパラメータを文脈に応じて変化させることで, より効率的に報酬を最大化することが可能になるだろうという想定をします.
以下では, 時刻$t$におけるあるアーム$a$からの報酬$r_{t, a}$は既知同一の分散$\sigma^2$を持つ正規分布に従うとします(Linear Stochastic Bandit). この時, これから紹介する2つのアルゴリズムは, 以下の(1)のように報酬をモデル化します. ここで, $\theta_a$ はアーム$a$に固有の真の線形モデルパラメータベクトルで, $x_{t, a}$が時刻$t$にアーム$a$について観測される文脈で, $\epsilon_t$はガウスノイズです.
r_{t, a} = \theta_a^{\mathrm{T}} x_{t, a} + \epsilon_t, \quad \epsilon_t \overset{i.i.d.}{\sim} Norm(0 | \sigma^2) \quad (1)
よって, 時刻$t$におけるアーム$a$からの報酬$r_{t, a}$は,
r_{t, a} \sim Norm(\theta_a^{\mathrm{T}}x_{t, a} | \sigma^2)
として得られるということになります.
このようなモデルを導入することで, アームの報酬情報のみから次の選択を決めていた古典的バンディットアルゴリズムとは異なり, Contextual Banditは報酬の確率分布に関する線形モデルパラメータを逐次的に推定します. そして, その推定値$\hat{\theta}_a$と文脈に基づいて各アームの報酬に想定する確率分布を変化させながら, 次に選択するアームを決めるアルゴリズムということになります.
LinUCB
ここでは, Contextual Bandit の草分け的論文である[1]で提案されたLinUCBを紹介します. LinUCBは以下の擬似コードに書かれたアルゴリズムで各時刻にアームを選択しながら, 観測される報酬と文脈の情報から線形モデルのパラメータ$\hat{\theta}_a$を逐次的に更新していきます.

ここで時刻$t$における線形パラメータの推定値は以下のように導かれ、擬似コードの12, 13行目のように更新されます. ($A_{a}$には逆行列が存在するとしています.)
\begin{align}
\hat{\theta}_a &= \arg \min_{\theta} \sum_{s=1}^t (r_{s, a} - \theta_a^{\mathrm{T}} x_{s, a} )^2 \\
& = \Bigl( \sum_{s=1}^t x_{s, a} x_{s, a}^{\mathrm{T}} \Bigr)^{-1} \sum_{s=1}^t r_{s, a} x_{s, a} \\
& =A_{a}^{-1} b_{a} \\
A_{a} &= \sum_{s=1}^t x_{s, a} x_{s, a}^{\mathrm{T}} , \; b_{a} = \sum_{s=1}^t x_{s, a} r_{s, a}
\end{align}
先ほど述べたように報酬が$r_{s, a} = \theta_a^{\mathrm{T}} x_{s, a} + \epsilon_s$ と表されることから,
\begin{align}
\hat{\theta_a} &= A_a^{-1} b_a \\
&= A_a^{-1} \sum_{s=1}^t x_{s, a} (\theta_a^{\mathrm{T}} x_{s, a} + \epsilon_s) \\
&= \theta_a + A_a^{-1} \sum_{s=1}^t x_{s, a} \epsilon_s
\end{align}
まず, 線形パラメータの推定量$\hat{\theta}_a$の期待値は誤差項の期待値がゼロであることから, 真のパラメータに一致します (不偏性).
\begin{aligned}
\mathbb{E}[\hat{\theta}_a] & = \mathbb{E} \Bigl[ \theta_a + A_a^{-1} \sum_{s=1}^t x_{s, a} \epsilon_s \Bigr] \\
& = \theta_a + A_a^{-1} \sum_{s=1}^t x_{s, a} \mathbb{E} [ \epsilon_s ] \\
& = \theta_a \quad (2)
\end{aligned}
次に, $\hat{\theta}_a$の分散は以下のようになります.
\begin{aligned}
\mathbb{V}[\hat{\theta}_a] & = \mathbb{E} \Bigl[ \bigl( \hat{\theta_a} - \theta_a \bigr) \bigl( \hat{\theta_a} - \theta_a \bigr)^{\mathrm{T}} \Bigr] \quad \because (2) \\
& = \mathbb{E} \Bigl[ \bigl( A_a^{-1} \sum_{s=1}^t x_{s, a} \epsilon_s \bigr) \bigl( A_a^{-1} \sum_{s=1}^t x_{s, a} \epsilon_s \bigr)^{\mathrm{T}} \Bigr] \\
& = A_a^{-1} \sum_{s=1}^t x_{s, a} \mathbb{E} [\epsilon_s \epsilon_s^{\mathrm{T}} ] \bigl( A_a^{-1} \sum_{s=1}^t x_{s, a} \bigr)^{\mathrm{T}} \\
& = \sigma^2 A_a^{-1}
\end{aligned}
よって, 擬似コード中9行目のようにLinUCBは各時刻$t$において報酬の不偏推定値から標準偏差の$\alpha$倍だけ大きく見積もった値が最も大きくなるアームを選択します. $\alpha$はハイパーパラメータで, 大きいほど探索を小さいほど活用を重視することを意味します. ここで, 擬似コード中の$A_a$の初期値が$d \times d$の単位行列になっているのは, 元論文においては線形パラメータを推定する際に, 単純な最小二乗推定ではなくて, Ridge推定 を用いているからです. 正則化パラメータを$\lambda$とした時に, Ridge推定解が以下のように求まるのはお馴染みですね.
\begin{aligned}
\hat{\beta}_{ridge} & = \arg \min_{\beta} \| Y - X \beta \|^2 + \lambda \| \beta \|^2 \\
& = (X^{\mathrm{T}} X + \lambda I)^{-1} X^{\mathrm{T}} Y
\end{aligned}
ですから, LinUCBは単位行列を初期値として持っているわけです.
(正則化パラメータ$\lambda$を掛けたものを初期値とすることもできそうですが, 論文ではそこまでしていませんでした.)
線形モデル上のThompson Sampling
先に紹介したLinUCBは, その名前からもわかるように典型的なバンディット問題におけるアルゴリズムの一つであるUCBアルゴリズムをContextual Banditに拡張したものだと言えます. そうなると自然な流れとして, こちらの記事で紹介したThompson SamplingのContextual Banditへの拡張も存在します. 次にその線形モデル上のThompson Sampling (以後, LinTS)について紹介します. アルゴリズムは以下の通りです.

まず, LinTSではLinUCBと同じように各アームの報酬が$r_{t, a} = \theta_a^{\mathrm{T}} x_{t, a} + \epsilon_t$と表せる場合を考えます. この時, $I$を$d \times d$の単位行列として線形パラメータ事前分布を$\theta_a \sim N(0 | \sigma_0^2 I_d)$と仮定すると, ベイズの定理より, $\theta_a$の事後分布が以下のように計算できます.
\begin{align}
p (\theta_a | \{ r_{s, a} \}^t_{s=1} ) &= \frac{p (\theta_a) \prod_{s=1}^t p(r_{s, a} | \theta_a )}{\prod_{s=1}^t p(r_{s, a} ) } \\
&\propto p (\theta_a) \prod_{s=1}^t p(r_{s, a} | \theta_a) \\
&\propto \exp \bigl(-\frac{\theta_a^{\mathrm{T}} \theta_a}{2\sigma_0^2} \bigr) \exp \bigl(-\frac{1}{2\sigma^2}\sum_{s=1}^t (r_{s, a} - \theta_a^{\mathrm{T}} x_{s, a} )^2 \bigr) \\
& \propto \exp \Biggl(-\frac{1}{2\sigma^2} \Bigl(\theta_a^{\mathrm{T}} \bigl(\frac{\sigma^2}{\sigma_0^2}I_d + \sum_{s=1}^t x_{s, a} x_{s, a}^{\mathrm{T}} \bigr)\theta_a + 2 \sum_{s=1}^t r_{s, a} x_{s, a}^{\mathrm{T}} \theta_a \Bigr) \Biggr) \\
& = \exp \Bigl( -\frac{1}{2\sigma^2} \bigl( \theta_a^T A_{t, a} \theta_a + 2b_{t, a}^{\mathrm{T}} \theta \bigr) \Bigr) \\
& \propto \exp \Bigl(-\frac{1}{2\sigma^2} (\theta_a - A_{t, a}^{-1}b_{t, a})^{\mathrm{T}} A_{t, a} (\theta_a - A_{t, a}^{-1}b_{t, a} ) \Bigr)
\end{align}
ここで, $A_{t, a} = \frac{\sigma^2}{\sigma_0^2}I_d + \sum_{s=1}^t x_{s, a} x_{s, a}^{\mathrm{T}} , ; b_{t, a} = \sum_{s=1}^t r_{s, a} x_{s, a}^{\mathrm{T}} $であることから, LinUCBの時と同じ式により$A_{t, a},, b_{t, a}$を更新します. そしてそれらを用いて各アームの線形パラメータの多変量正規事後分布$MultiNorm(A_{t, a}^{-1}b_{t, a} | \sigma^2 A_{t, a}^{-1})$から$\tilde{\theta}$をサンプリングします. そうして得られたパラメータと文脈の線形和$\tilde{\theta}^{\mathrm{T}} x_{t, a}$が最も大きくなるアームを選択するのが, LinTSになります. 基本的な考え方は通常のバンディット問題におけるThompson Samplingと同じで, LinUCBと同じようにContextual Banditの設定に自然に拡張したアルゴリズムと考えていいでしょう.
ロジスティック回帰とThompson Sampling
これまでは, 報酬構造モデルとして, 誤差項$\epsilon_t$が正規分布に従う場合のアルゴリズムを紹介してきました. しかし, Netflixの例などでは作品のレコメンドについてユーザーが視聴するか否かの2値変数を目的変数としたい場合が考えられます. このような場合に, 目的変数の誤差項は明らかに正規分布には従いません. よって目的変数が2値変数の場合は以下のような報酬構造のモデル化を考えることがあります.
\mathbb{P}(r_{t, a} = 1) = \frac{e^{\theta_a^{\mathrm{T}} x_{t, a}}}{1 + e^{\theta_a^{\mathrm{T}} x_{t, a} }}
つまり, よく用いられるロジスティック回帰と同じように, 報酬が1を取る確率のロジットが文脈の線形和で表されるというモデル化です. このモデル化においても, 以下のように時刻$t$における最適なアームは文脈と真の線形パラメータの線形和を最大化するアームになります.
a^{ * }(t) = \arg \max_a \frac{e^{\theta_a^{\mathrm{T}} x_{t, a}}}{1 + e^{\theta_a^{\mathrm{T}} x_{t, a} }} = \arg \max_a \theta_a^{\mathrm{T}} x_{t, a}
この報酬モデルにおけるThompson Samplingのアルゴリズムを導くために線形パラメータ$\theta_a$の事後分布を導出したいのですが, 先程まで用いていた線形回帰モデルとは異なり今回のロジスティック回帰モデルでは, 事後分布を解析的に求めることはできません. よって以下ではラプラス近似で線形パラメータの事後分布を変量正規分布に近似した上でサンプリングするという手順を踏みます. まずは, ロジスティック回帰モデルにおける事後分布を書き下していきます.
\begin{align}
p (\theta_a | \{ r_{s, a} \}^t_{s=1} ) &= \frac{p (\theta_a) \prod_{s=1}^t p(r_{s, a} | \theta_a )}{\prod_{s=1}^t p(r_{s, a} ) } \\
& \propto p (\theta_a) \prod_{s=1}^t p(r_{s, a} | \theta_a ) \\
& \propto p (\theta_a) \prod_{s=1}^t \Biggl( \frac{e^{\theta_a^{\mathrm{T}} x_{s, a}}}{1 + e^{\theta_a^{\mathrm{T}} x_{s, a} }} \Biggr)^{r_{s, a}} \Biggl( \frac{1}{ 1 + e^{\theta_a^{\mathrm{T}} x_{s, a} }} \Biggr)^{1 - r_{s, a}} \\
& \propto e^{- \frac{\theta_a^{\mathrm{T}} \theta_a}{2\sigma_0^2}} \prod_{s=1}^t \frac{1} { 1 + e^{\theta_a^{\mathrm{T}} x_{s, a} }} \prod_{s: \; r_{s, a} = 1} e^{\theta_a^{\mathrm{T}} x_{s, a}}
\end{align}
$\theta_a$に関係する項に注目した負の対数事後分布は,
\begin{align}
& - \log p (\theta_a | \{ r_{s, a} \}^t_{s=1} ) \\
& = \frac{\theta_a^{\mathrm{T}} \theta_a}{2\sigma_0^2} + \sum_{s=1}^t \log \bigl( 1 + e^{\theta_a^{\mathrm{T}} x_{s, a} } \bigr) - \sum_{s: \; r_{s, a} = 1} \theta_a^{\mathrm{T}} x_{s, a} + const.
\end{align}
となります. この負の対数事後分布の勾配ベクトルとヘッセ行列は以下のように計算できます. ベクトルによる微分公式はこちらにまとまっています.
\begin{align}
G_t(\theta_a) & = - \nabla_{\theta_a} \log p (\theta_a | \{ r_{s, a} \}^t_{s=1} ) \\
& = \frac{\theta_a}{\sigma_0^2} + \sum_{s=1}^t \frac{e^{\theta_a^{\mathrm{T}} x_{s, a}} x_{s, a}}{1 + e^{\theta_a^{\mathrm{T}} x_{s, a} }} - \sum_{s: \; r_{s, a} = 1} x_{s, a} \\ \\
H_t(\theta_a) & = - \nabla_{\theta_a}^2 \log p (\theta_a | \{ r_{s, a} \}^t_{s=1} ) \\
& = \frac{I_d}{\sigma_0^2} + \sum_{s=1}^t \frac{e^{\theta_a^{\mathrm{T}} x_{s, a}} x_{s, a} x_{s, a}^{\mathrm{T}}}{ \bigl( 1 + e^{\theta_a^{\mathrm{T}} x_{s, a} } \bigr)^2}
\end{align}
ここで前述の通り, $G_t(\theta_a) = 0$を満たすMAP推定量$\hat{\theta}^{ MAP }_a$は解析的に求めることができませんが, 以下の反復を繰り返すニュートン法により数値的に求めます.
\begin{aligned}
\hat{\theta}_a (l + 1) \leftarrow \hat{\theta}_a (l) - H_t \bigl( \hat{\theta}_a (l) \bigr)^{-1} G_t \bigl( \hat{\theta}_a (l) \bigr)
\end{aligned}
このニュートン法により求まったMAP推定解の周りで先ほどの負の対数尤度を2次近似します. ここで, $G_t\bigl( \hat{\theta}_a^{MAP} \bigr) \approx 0 $とすると,
\begin{aligned}
& - \log p (\theta_a | \{ r_{s, a} \}^t_{s=1} ) \\
& \approx \frac{1}{2} (\theta_a - \hat{\theta}_a^{MAP} )^{\mathrm{T}} H_t(\hat{\theta}_a^{MAP}) (\theta_a - \hat{\theta}_a^{MAP} ) + const. \quad (3)
\end{aligned}
となります. ここでよく見ると, (3)は多変量正規分布の確率密度関数と同じ形になっていることに気付きます. よって, 解析的に求められない事後分布を, ニュートン法などで求めたMAP推定量を平均に, ヘッセ行列の逆行列を分散共分散行列に持つ多変量正規分布$MultiNorm \Bigl(\hat{\theta}_a^{MAP}, \bigl( H_t(\hat{\theta}_a^{MAP}) \Bigr)^{-1} \bigr)$で近似するのがラプラス近似になります. そして, この近似した事後分布から線形パラメータをサンプリングすることで, ロジスティック回帰モデルを用いた時のThompson Samplingを構成することができます. 擬似コードは以下の通りです.

実験
本記事で紹介したアルゴリズムの性能を調べるため2つの実験を行いました. 実験を行なったノートブックはこちらになります. また, 今回記事を書くにあたって, 古典的なバンディットアルゴリズムや今回紹介した3つのContextual BanditのアルゴリズムなどをPyMABというライブラリを実装してみました. 以降の実験ではこのPyMABを用いています.
実験1(誤差項が正規分布)
- 配信回数15,000回の中で作品の視聴時間など(目的変数が連続)を最大化するという状況設定.
- 各アルゴリズムのパラメータ推定値は300回の試行につき1回更新できるものとする.
- LinTSは$\tilde{\theta}$のサンプリングが速度的なボトルネックであるため, 15回の試行につき1回サンプリング.
- 50回のシミュレーションにおける平均累積リグレットで性能比較.
比較アルゴリズム
| アルゴリズム | ハイパーパラメータ |
|---|---|
| ε-greedy (比較用) |
$\epsilon = 0.1$ |
| LinTS | $\sigma_0 = 0.1$ |
| LinTS | $\sigma_0 = 1$ |
| LinUCB | $\alpha = 0.1$ |
| LinUCB | $\alpha = 1$ |
アームの作り方
- 5種類のアーム(Artworkの選択肢)を用意.
- 各アームは15次元の真の線形パラメータ$\theta_a$を平均0, 分散0.1の正規分布から独立に得る.
特徴量の作り方
- 文脈は全て0 or 1の離散値とし, 各ユーザーについて15次元の文脈が観測される. (ダミー変数)
結果
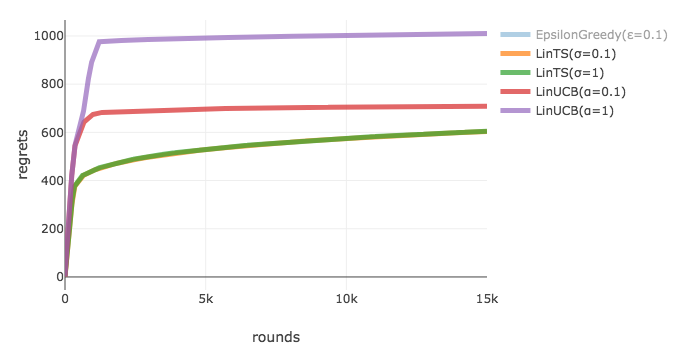
以下が, 各配信回数ごとの累積リグレットの推移を表した図になります. Epsilon Greedyは明らかに他よりも性能が悪かったためグラフからは除きました. これをみると, LinUCBよりもLinTSの方が累積リグレットを小さく抑えることができています. 今回はパラメータの推定値がバッチ更新される場合を扱いましたが, アルゴリズムを見ればわかるようにLinUCBはパラメータの推定値が同じであればずっと同じアームを選択し続けるため, 全てのアームに関する情報を集めるのに時間がかかったと思われます. 一方で, LinTSはパラメータの推定値が同じでも, 選択するアームは多変量正規分布からサンプリングしてきた線形パラメータに基づくのでバッチ更新に対して頑健だったということがわかります. ちなみに, 緑と黄色の線はほぼ重なっているのですが, 15,000回も配信していると線形パラメータの事前分布の違いはあまり関係なくなることが見てとれます.
実験2(報酬が2値変数)
- 配信回数15,000回の中で作品の視聴回数など(目的変数が離散)を最大化するという状況設定.
- そのほかの設定は実験1と同じ.
比較アルゴリズム
| アルゴリズム | ハイパーパラメータ |
|---|---|
| ε-greedy (比較用) |
$\epsilon = 0.1$ |
| LinUCB | $\alpha = 0.1$ |
| LinTS | $\sigma_0^2 = 0.1$ |
| LogisticTS | $\sigma_0^2 = 0.1$ |
結果
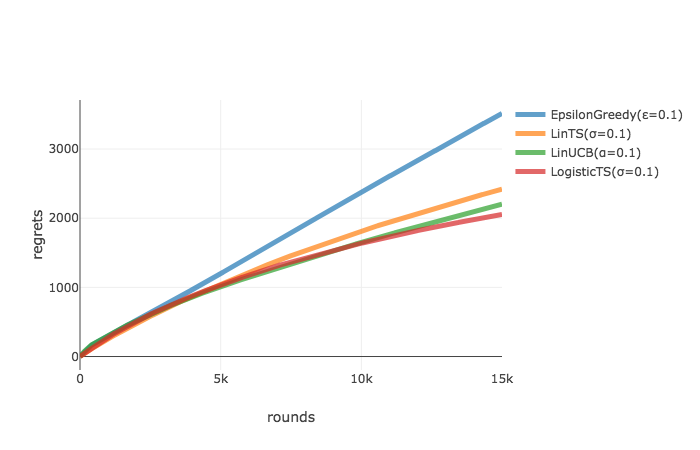
実験2の累積リグレットの推移は以下のようになりました. あまり大きな差はありませんが, LogisticTSが最も小さい累積リグレットを達成しています. またどのアルゴリズムもまだリグレットが増えている傾向にあることから, 配信回数を増やすにつれてLogisticTSが他との差を大きく開いていきそうな傾向も見て取れます. 報酬構造に合わせてそれに適したContextual Banditアルゴリズムを用いることの有効性を確認できました.
Part 2への繋ぎ
今回は, 元記事で詳細が解説されていなかったこともあり, Contextual Banditアルゴリズムにおいて基礎的なLinUCB, LinTS, LogisticTSを紹介し, シミュレーションで評価を行いました.
しかし, Contextual Banditを実運用することを考えると新たなArtworkが追加されるたびに実システム上でアルゴリズムを走らせて性能を評価していては, ユーザー体験を大きく害してしまう危険性があります. 性能が悪いアルゴリズムやハイパーパラメータは, 実運用する前に候補から省いておきたいですよね。
そのためには, 何れかのアルゴリズムによってすでに蓄積されたデータ を用いて, 新たなアルゴリズムや異なるハイパーパラメータを評価する必要が出てきます. これをOff-Policy Evaluation(OPE) と呼びますが, 実は私が最も興味があるのは, アルゴリズムそのものというよりもこのOPEです. 次回のPart 2では, Netflixが実際に使っているOffline評価手法を紹介した後に, もっと踏み込んだ最新の評価方法を紹介するつもりです!
追記:Part 2を書きました.
参考
[1] Li, Lihong, Chu, Wei, Langford, John, and Schapire, Robert E. A contextual-bandit approach to personalized news article recommendation. In Proceedings of the 19th International Conference on World Wide Web, pp. 661–670. ACM, 2010.
[2] 本多淳也, 中村篤祥. バンディット問題の理論とアルゴリズム. 講談社 機械学習プロフェッショナルシリーズ, 2016.
[3] Chapelle, Olivier and Li, Lihong. An Empirical Evaluation of Thompson Sampling. In Neural Information Processing Systems, pp. 2249–2257, 2011.