More than 5 years have passed since last update.

Netflixを超えていけ！Contextual Banditアルゴリズムを徹底解説！（Part 2）

Last updated at 2018-11-06Posted at 2018-11-06

はじめに

Part 1では, NetflixがArtworkの個別化に使っているContextual Banditについて解説し, 実験まで行いました. Part 1で行った実験は, アルゴリズムを実際のシステムで走らせた時の性能評価を想定していましたが, 実際そのように理想的なアルゴリズムの性能評価を行うことが難しい場合が多い です. 何故ならば, あるアルゴリズムを一定期間実際のサービスで走らせた上で性能を評価したいと思っても, それが性能の悪いものであったら, ユーザー体験を害してしまったりサービスからの収入に影響があるかもしれないからです.

したがって,

何かしらのアルゴリズムにより既に蓄積されたデータのみを用いて,
新しいアルゴリズムを適用したときの評価を事前に見積もりたい.

というモチベーションが生まれます.

このような問題設定をOff-Policy Evaluation(OPE) と呼び, 実際にNetflixも記事中で, Offline評価により性能の良いアルゴリズムの候補を絞ってからOnline評価により, ベストなアルゴリズムを決定するという手順を踏んでいると書いていました.

今回の記事では, OPEの枠組みを定式化した上で, Netflixが用いているReplay methodを紹介します. さらに後半では, そのReplay methodよりさらに踏み込んだ最新の手法をいくつか紹介し, 実験でそれらの性能を評価します.

Off-Policy Evaluation(OPE)の定式化

Off-Policy Evaluationの難しさ（と面白さ）はCounterfactualが不可知であるという問題に集約されます.

この問題は,

過去のPolicyと新たなPolicyは同じ文脈でも異なるアームを選ぶかもしれない
もちろんログデータには, 過去のPolicyが選択したアームからの情報しか含まれない
本当は新しいPolicyが選ぶアームからの報酬情報を用いて性能を評価したいが不可知なので無理...

ということです. この時, ログデータで実現しているデータをFactual実現していないデータをCounterfactualと呼ぶことがあるのですが, Counterfactualをどう評価するのかがOPEの大きな焦点 になります.

今, 時刻$t$において観測される文脈（ユーザー特徴量など）を$X_t \in \mathbb{R^d}$, 選択されるアーム（Artworkの選択肢など）を$A_t \in {1, 2, 3, ..., K}$, 観測される報酬（ユーザーの作品視聴確率など）を$R_t \in \mathbb{R}$とします. この時, あるPolicy $\pi$を以下のように時刻$t$ににおいてどのアームを選択するかを決定するものとします.

A_t \sim \pi \left( . | X_t \right)

仮に$t$で$A_t = a_t$を選び$R_{a_t} = r_{a_t}$が観測されたとしても, $a_t$以外のアーム$\forall a_t' \neq a_t$を選択できたはずで, $a_t'$を選択したら$R_{a_t'}$からの報酬が観測されていたでしょう. つまり, Counterfactualな状況は, $t$において潜在的には${R_1, R_2, R_3, ..., R_K }$の$K$個の潜在的な目的変数が存在するはずだが, 選ばれた$a_t$に対応する目的変数$R_{a_t}$からの実現値$r_{a_t}$しか観測されない状況として特徴付けることができます.

この時, このPolicy $\pi$の性能は以下のように定義できます.

V(\pi) = \mathbb{E}_{X, R} \left[ R_{\pi(X)} \right]

もちろん, $\pi$ を実システムで一定期間走らせた上で得た目的変数は, $V(\pi)$の一つの実現値になります. しかし, そのような理想的な性能評価が困難な場合は, 何れかのPolicy $\pi^{past}$ によって集められた過去のデータ $S = \left(x_t, a_t, r_t \right)_{t=1}^T $ を用いて新たなPolicyについての $V(\pi)$ を推定しなければなりません. OPEでは, 過去のログを用いて真の性能$V(\pi)$とのMSE（以下の式）がより小さい推定量$\hat{V}(\pi)$を構築することを目指します.

\begin{aligned}
MSE \left( V(\pi), \hat{V}(\pi) \right) &= \mathbb{E} \left[ \left( V(\pi) - \hat{V}(\pi) \right)^2 \right] \\
& = Bias \left( V(\pi), \hat{V}(\pi) \right) ^2 + Var \left( \hat{V}(\pi) \right)
\end{aligned}

Replay method

ここでは, Netflixが使っているReplay method[1]を紹介します. Replay methodは, 評価したいPolicy $\pi^{new}$を$\pi^{past}$によるログ$S$上で走らせ, 図のように時刻$t$において$\pi^{past}$と$\pi^{new}$が選択したアームが一致した場合の報酬を平均して$\pi^{new}$の性能の評価値とします.

Artwork Personalization at Netflixより
（User1, 2, 4に対するArtworkの選択が$\pi^{past}$と$\pi^{new}$で一致したので, それらのみを用いている.）

つまり, Replay methodは以下の式で$\pi^{new}$の性能を推定しています.

\begin{aligned}
\hat{V}_{replay}(\pi^{new}) = \frac{1}{\sum_{t=1}^T \mathbb{I}\{\pi^{new}(x_t) = a_t \}} \sum_{t=1}^T r_t \mathbb{I}\{\pi^{new}(x_t) = a_t \}
\end{aligned}

Replay methodがOffline評価指標として正当性を持つのは, もしも$\pi^{past}$が離散一様分布に従ってランダムにアームを選ぶPolicyだった場合に, 任意の$\pi^{new}$ を$S$上で走らせた場合と, 真の同時確率分布$(x, r)$上で走らせた場合に生成される事象列の確率分布が等しくなるからです. よって, 以下のように$\hat{V}_{replay}(\pi^{new})$は不偏性を持ちます. （上の図において$\pi^{past}$がRandom Assignmentと記載されているのはこのためです.）

\mathbb{E} \left[ \hat{V}_{replay}(\pi^{new}) \right] = V(\pi^{new})

もちろんReplay methodのこの性質は望ましいものですが, $S$がランダムなPolicy $\pi^{past}$(A/Bテスト)
によって集められていなければならないという大きな欠点があります.

先に述べたようにOPEの目的の一つに, 機会損失をなるべく小さくした上で, $\pi^{new}$を正確に評価したいというものがあります. NetflixもReplay methodを用いるためにランダムなPolicyによってデータを集めているようでした. しかし, 新たな作品やArtworkが追加されるたびにランダムなPolicyによってデータを集めるのはコストが大きい と考えられるため, 次章ではNetflixのシステムをさらに改善させられる可能性がある最新の評価指標をいくつか紹介します.

最新の評価指標 (DM, IPS, DR, MRDR)

本章では, 最新のOPE手法を4つ紹介しますが, その内有力な手法とされているのは後半の2つ（DRとMRDR）です. しかしそれらは前半の2つ（DMとIPS）に基づいて構成されるので, そのつもりで読んでいただけたらと思います.
また, 以降のBiasやVarianceの導出では表記の簡略化のため誤解が生まれないと判断した範囲で$(x_t)$の表記を省いています.

Direct method (DM)

DMの基本コンセプトは「Counterfactualを予測して埋めよう」というものです. まず, $S$を各アームごとに分けて, それぞれで文脈$x$から報酬$r$を予測するモデル$\hat{\rho}_a(x) \approx \rho_a(x) = \mathbb{E} [r_a | x]$を学習します. それを用いて以下のように推定値を計算します.

\hat{V}_{DM}(\pi^{new}) = \frac{1}{T} \sum_{t=1}^T \hat{\rho}_{\pi^{new}(x_t)}(x_t)

報酬の予測モデルの精度を, $\Delta(a, x) = \hat{\rho}_a(x) - \rho_a(x)$とすると, DMのBiasは以下のように表せ, 報酬の予測モデルの精度に依存します.

\begin{aligned}
Bias \left( \hat{V}_{DM}(\pi^{new}) \right) &= \left| \mathbb{E} \left[ \hat{V}_{DM}(\pi^{new}) \right] -  V(\pi^{new}) \right| \\
&= \mathbb{E}_x \left[ \Delta(\pi^{new}, x) \right]
\end{aligned}

しかし, $\Delta$を小さくするために乗り越えなければならない問題がいくつかあります. まず一つ目は, アームが多ければ多いほど, アームごとに精度の良い報酬の予測モデルを構築するために$|S|$を大きくしなければならないことです. より重要なのが2つ目の問題点で, $\pi^{past}$がランダムなPolicyではない場合, $a \neq a'$について, $p(x | a) \neq p(x | a')$となるアームの組み合わせが存在するため, ソースドメインとターゲットドメインの文脈の確率分布が異なるというドメイン適応と同じ問題設定になっています. これに対して[2]では, 報酬モデルを構築する際の損失関数の設計については触れられていません. しかし, 単純な損失関数による予測モデルを適用させただけでは, 小さな$\Delta$は期待できないと考えられます.

Inverse Propensity Score (IPS)

$p(x | a) \neq p(x | a')$という問題に因果推論におけるPropensity Score (こちらの記事に解説があります)の考え方を用いるのがIPSです. Propensity Scoreは以下のように定義されます.（注1）

p_a = \mathbb{P} (a | x)

つまりPropensity Scoreとは, 文脈$x$に対してアーム$a$を選択する確率のことです. これを用いて以下のような推定量を構築するのがIPSです.

\hat{V}_{IPS}(\pi^{new}) = \frac{1}{T} \sum_{t=1}^T \frac{r_{a_t }  \mathbb{I}\{\pi^{new}(x_t) = a_t \}}{p_{a_t}}

次の2つの仮定を置くと, IPSは不偏性を持ちます. 1つ目は, 真のPropensity Scoreがわかっているというものです. これはNetflixのように$\pi^{past}$を自分で決めていて（ランダムである必要はない）かつ, サービスが自社内で閉じている時には妥当な仮定と言えます. もしも真のPropensity Scoreがわかっていなかったとしてもロジスティック回帰などでPropensity Scoreの一致推定量が得られれば, IPSも一致性を持ちますし, Biasの分析も可能です[2]. 2つ目の仮定は因果推論ではUnconfoudnednessと呼ばれるもので, 以下のように表されます.

(R_1, R_2, R_3, ... , R_K) \perp A_t \, | \, X_t \quad \forall t \in \{1, 2, ..., T \}

これは, アームが観測されている文脈$X_t$のみから決定されていなければならないと解釈できますが, これもNetflixのケースのように$\pi^{past}$を自分で決めていて, サービスが自社内で閉じている場合は満たしているものと考えて良いでしょう. この時,

\begin{aligned}
\mathbb {E} \left[ \hat{V}_{IPS}(\pi^{new}) \right] & = \mathbb {E} \left[ \frac{1}{T} \sum_{t=1}^T \frac{r_{a_t }  \mathbb{I}\{\pi^{new} = a_t \}}{p_{a_t}} \right] \\
& = \frac{1}{T} \sum_{t=1}^T \mathbb {E} \left[ \frac{r_{a_t }  \mathbb{I}\{\pi^{new} = a_t \}}{p_{a_t}} \right]  \\
& = \frac{1}{T} \sum_{t=1}^T \mathbb{E}_x \left[ \mathbb{E}_{r|x} \left[ r_{\pi^{new}} \right]  \mathbb {E}_{a|x} \left[ \frac{ \mathbb{I}\{\pi^{new} = a_t \}}{p_{\pi^{new}}} \right] \right]  \\
&= \frac{1}{T} \sum_{t=1}^T \mathbb{E} \left[ r_{\pi^{new}} \right] \\
& = V(\pi^{new}) \\ \\
\mathbb {V} \left[ \hat{V}_{IPS}(\pi^{new}) \right] & = \frac{1}{|S|}\left( \mathbb{E}_{x, r, a} \left[ \epsilon^2 \right] + \mathbb{V}_x  \left[ \rho_{\pi^{new}} \right] + \mathbb{E}_x \left[ \frac{1-p_{\pi^{new}}}{p_{\pi^{new}}} \rho_{\pi^{new}}^2 \right] \right) \\
& where \quad \epsilon = \frac{(r_{a_t} - \rho_{a_t}) \mathbb{I} \{ \pi^{new} = a_t \} }{p_a}
\end{aligned}

となります. IPSはPropensity Scoreによりアーム間の分布の違いを補正し, 不偏性を持ちます. Varianceの詳しい導出は[2]のTheorem 2をご覧いただけたらと思いますが, 推定量の2次モーメントを計算した後に期待値を使うと導けます. また, 第三項からPropensity Scoreがとても大きかったり, 小さかったりする時にIPSの分散がとても大きくなってしまう問題が示唆されます.

Doubly Robust (DR)

DRはIPSのVarianceが大きくなってしまうという問題点をDMをうまく組み合わせることにより改善した手法です. DRは以下のように$\pi^{new}$の性能を推定します．

\hat{V}_{DR}(\pi^{new}) = \frac{1}{T} \sum_{t=1}^T \left( \frac{(r_{a_t } - \hat{\rho}_{a_t}  )\mathbb{I}\{\pi^{new}(x_t) = a_t \}}{p_{a_t}} + \hat{\rho}_{\pi^{new}(x_t)} \right)

DRによる性能の推定はIPSと同様に不偏性を持ちつつ, Varianceを小さく抑えることが期待されます.

\begin{aligned}
\mathbb {E} \left[ \hat{V}_{DR}(\pi^{new}) \right] & = \mathbb {E} \left[ \frac{1}{T} \sum_{t=1}^T \left( \frac{(r_{a_t } - \hat{\rho}_{a_t}  ) \mathbb{I}\{\pi^{new} = a_t \}}{p_{a_t}} + \hat{\rho}_{\pi^{new}} \right) \right] \\
& = \frac{1}{T} \sum_{t=1}^T \mathbb {E} \left[ \frac{1}{T} \sum_{t=1}^T \left( \frac{(r_{a_t } - \hat{\rho}_{a_t}  )\mathbb{I}\{\pi^{new} = a_t \}}{p_{a_t}} + \hat{\rho}_{\pi^{new}} \right) \right] \\
& = \frac{1}{T} \sum_{t=1}^T \left( \mathbb{E}_x \left[  \mathbb{E}_{r|x} \left[ r_{\pi^{new}} - \hat{\rho}_{\pi^{new}} \right]  \mathbb {E}_{a|x} \left[ \frac{ \mathbb{I}\{\pi^{new} = a_t \}}{p_{\pi^{new}}} \right] \right]  + \mathbb{E} \left[ \hat{\rho}_{\pi^{new}} \right]\right)\\
&= \frac{1}{T} \sum_{t=1}^T \mathbb{E} \left[ r_{\pi^{new}} \right] \\
& = V(\pi^{new}) \\ \\
\mathbb {V} \left[ \hat{V}_{DR}(\pi^{new}) \right] & = \frac{1}{|S|}\left( \mathbb{E}_{x, r, a} \left[\epsilon^2 \right] + \mathbb{V}_x \left[ \rho_{\pi^{new}} \right] + \mathbb{E}_x \left[ \frac{1-p_{\pi^{new}}}{p_{\pi^{new}}} \Delta\left(\pi^{new}, x \right)^2 \right] \right)
\end{aligned}

こちらのVarianceも[2]のTheorem 2に導出があります. 第三項を見ると$\rho_{\pi^{new}}$が$\Delta\left(\pi^{new}, x \right)$に変わっていることがわかります. $\Delta\left(\pi^{new}, x \right)$は$\rho_{\pi^{new}}$に対する予測モデルでしたから, その予測残差が目的変数の期待値よりも小さければ, DRのVarianceはIPSよりも小さいということを意味します. よってDRは, Offline評価指標として（多くの場合）より望ましい性質を持ちます.

More Robust Doubly Robust (MRDR)

MRDRは今年3月にDeepMindが発表した手法[5]で, DRのVarianceをちょっとした工夫でさらに小さくする手法 です. まず, DRのVarianceの式で$\epsilon$として丸め込んでいたものをバラして以下のように変形します. (以降は, 本記事の設定やNotationに合わせて私自身が論文とは別の方法で変形しています. 何か間違いがあれば, ご指摘いただけると幸いです.)

\begin{aligned}
\mathbb {V} \left[ \hat{V}_{DR}(\pi^{new}) \right] & = \frac{1}{|S|} \Biggl( \mathbb{E}_{x, r, a} \left[ \frac{(r_{\pi^{new}} - \rho_{\pi^{new}})^2 \mathbb{I}}{p_{\pi^{new}}^2} \right] + \mathbb{E}_x \left[ \rho_{\pi^{new}}^2 \right] - \mathbb{E}_{x, r} \left[ r_{\pi^{new}} \right]^2  \\
\quad & + \mathbb{E}_{x, r} \left[ \frac{1-p_{\pi^{new}}}{p_{\pi^{new}}} \left( \hat{\rho}_{\pi^{new}}^2 -2 r_{\pi^{new}} \hat{\rho}_{\pi^{new}} + \rho_{\pi^{new}}^2  \right) \right] \Biggr) \\
&= \frac{1}{|S|} \Biggl( \mathbb{E}_{x, r, a} \left[ \frac{ \mathbb{I}\left(1 - p_{\pi^{new}} + p_{\pi^{new}} \right)}{p_{\pi^{new}}^2}r_{\pi^{new}}^2 \right] - \mathbb{E}_x \left[ \frac{1}{p_{\pi^{new}}} \rho_{\pi^{new}}^2  \right] + \mathbb{E}_x \left[ \rho_{\pi^{new}}^2 \right] \\
\quad & - \mathbb{E}_{x, r} \left[ r_{\pi^{new}} \right]^2  + \mathbb{E}_{x, r, a}  \left[ \frac{ \mathbb{I} \left(1-p_{\pi^{new}} \right) }{p_{\pi^{new}}^2} \left( \hat{\rho}_{\pi^{new}}^2 -2 r_{\pi^{new}} \hat{\rho}_{\pi^{new}} \right) \right] + \mathbb{E}_x \left[ \frac{1-p_{\pi^{new}}}{p_{\pi^{new}}} \rho_{\pi^{new}}^2  \right] \Biggr) \\
&=  \frac{1}{|S|} \left( \mathbb{V}_{x, r} \left[r_{\pi^{new}}  \right] + \mathbb{E}_{x, r, a} \left[ \frac{ \mathbb{I} \left(1-p_{\pi^{new}} \right) }{p_{\pi^{new}}^2} \left( r_{\pi^{new}} - \hat{\rho}_{\pi^{new}} \right)^2 \right] \right)
\end{aligned}

ここで, $\mathbb{I}(\pi^{new} = a_t )$を$\mathbb{I}$と簡略化しました. 第一項は予測モデルに非依存であり, 第二項に注目すると予測モデルを報酬に対する単純な最小二乗則にしたがって学習するのではなく, サンプルごとに$\frac{1-p_{\pi^{new}}}{p_{\pi^{new}}^2}$で重み付けした損失関数を用いることで推定量の分散をさらに小さくできる ことが示唆されます. よって, DRに用いていた報酬に対する予測モデル$\hat{\rho}_{\pi^{new}}$を以下のように学習するのがMRDRになります.

\begin{aligned}
\hat{\rho}_{\pi^{new}}^{ * } \in \arg \min_{\hat{\rho}} \frac{1}{T} \sum_{t=1}^T \mathbb{I} \{ \pi^{new} = a_t \}  \frac{1-p_{\pi^{new}}}{p_{\pi^{new}}^2} \left( r_t - \hat{\rho}_{a_t} \right)^2
\end{aligned}

MRDRは, IPSやDRで分散が大きくなってしまう原因だったPropensity Scoreが大きかったり小さかったりするサンプルの報酬に対する予測モデルの予測精度を重視した損失関数を用いることで, 分散を小さくしていると解釈できます.

実験

ここでは, これまでに紹介してきた評価指標の性能を2つの状況を想定した実験により評価します. (注2)

実験1

設定

アーム数は10, 文脈の次元は20次元のバンディットに対する報酬最適化
離散一様分布に従うランダムPolicy によって集められたデータ数5万のログデータを用いたOPE
これらの指標を用いて以下の4つのPolicyの性能を推定

アルゴリズム	ハイパーパラメータ
LinUCB	$\alpha = 0.1$
LinUCB	$\alpha = 0.01$
LinUCB	$\alpha = 1$
LinUCB	$\alpha = 10$
LinTS	$\sigma_0^2 = 0.01$

用いる評価指標はReplay methodとDirect method（予測モデルには勾配ブースティングを使用）
評価指標の性能は各Policyの真の性能*と推定された性能の相対誤差によって評価（以下の式）

error_{metrics} = \frac{\hat{V}_{metrics} - V_{true}}{\left| V_{true} \right|}

*それぞれのアルゴリズムを, 30回Onlineで走らせて得た報酬を平均して算出.

なお, 実験1で使用したノートブックはこちらからご覧になれます.

結果

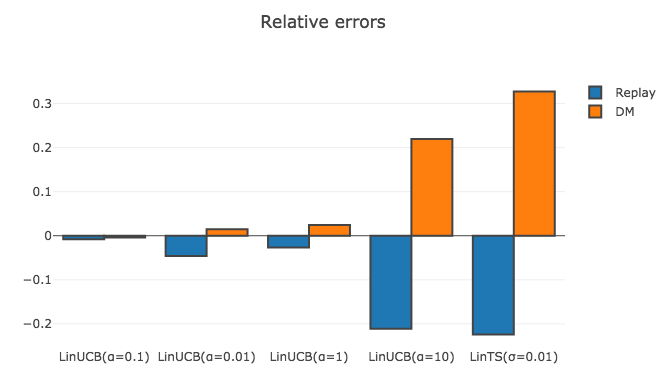
以下が各評価指標と新たなPolicyの候補の組み合わせごとの相対誤差になります.

	LinUCB(0.1)	LinUCB(0.01)	LinUCB(1)	LinUCB(10)	LinTS(0.01)	選んだPolicy
Replay	-0.008	-0.046	-0.027	-0.211	-0.224	LinUCB(0.1)
DM	-0.004	0.015	0.024	0.219	0.327	LinUCB(0.1)

実験1では, ログデータがランダムPolicyによって集められた望ましい性質を持つデータでしたので, ReplayやDirectといったシンプルな方法で各Policyの性能を小さい誤差で推定できています. 事実, Online環境で最も報酬を稼いだ手法はLinUCB($\alpha=0.1$)だったのですが, 2つの評価指標ともLinUCB($\alpha=0.1$)の性能の推定値が最大であり, ログデータを用いて正しい選択ができました.

実験2

設定

LinUCB($\alpha=1$) によって集められたデータ数5万のログデータを用いたOPE
用いる評価指標は実験1のものに加えて, IPS, DR, MRDR（予測モデルには勾配ブースティングを使用）
それ以外の設定は実験1と同じ

なお, 実験2で使用したノートブックはこちらからご覧になれます.

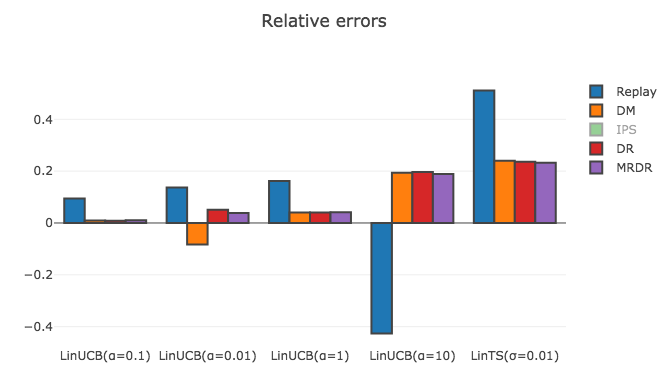
結果

以下が, 各評価指標と新たなPolicyの候補の組み合わせごとの相対誤差になります.（* 非常に僅差だったので有効数字を一桁増やしています.）

	LinUCB(0.1)	LinUCB(0.01)	LinUCB(1)*	LinUCB(10)	LinTS(0.01)	選んだPolicy
Replay	0.095	0.137	0.1619	-0.426	0.512	LinUCB(1)
DM	0.010	-0.083	0.0401	0.194	0.240	LinUCB(0.1)
IPS	0.310	1.442	0.3559	-16.470	2.658	LinTS(0.01)
DR	0.008	0.051	0.0405	0.196	0.237	LinUCB(0.01)
MRDR	0.010	0.039	0.0410	0.189	0.232	LinUCB(0.1)

IPSの相対誤差がとても大きかったため, 描画からは除きました. 今回は, ログデータ上で各Policyを一回走らせたのみで性能を評価していますので, Varianceの問題がより顕著に現れたと考えられます. 実際に用いる際は, Bootstrap法 を用いてVarianceを抑えるなどの対策が考えられます.

結果を見てみると, Replay methodは全てのPolicyに対する相対誤差が実験1よりも大きくなってしまっていることがわかります. よって, Replay methodを実験2の設定にそのまま適用するのは無理があります. 一方で, DRやMRDRの推定が最も正確 であることが見て取れます. （案外Direct methodも良い推定精度を見せていますが, LinUCB($\alpha=0.01$)に対する誤差が少し大きいです.）これらの評価指標は, 実験1におけるReplay methodと遜色ない（むしろ勝っていそう）推定精度を見せていますし, MRDRについてはLinUCB($\alpha=0.1$)の性能の推定値が最大であり, ログデータを用いて正しい選択ができていました. よって, MRDRといった最新の評価指標を用いることにより, Netflixが使っているOffline評価よりも低コストかつ正確な評価が達成可能であることが示唆されました.

まとめ

今回は, Off-Policy Evaluationの最新手法としてMore Robust Doubly Robustまで紹介し, 数値実験によりそれらの評価指標としての性能を比較検証しました. 私自身新たな予測モデルやアルゴリズムに基づいた介入施策を検証しようと思っても時間やコストの関係でA/Bテストを用いた実験的な評価が難しいと感じることがあります. そんな場面で, 過去のPolicyに基づいて得られたログデータから新しいPolicyの性能を評価する手法群は大いに役立ち, 試行錯誤のスピードを上げてくれるのではないかと期待を寄せています.

(注1)
今回はPropensity Scoreを, $p_a = \mathbb{P}(a | x)$と定義しましたがこれは, [2]においてstationaryとされている状況設定です. しかしバンディットを考える上でこの状況設定は現実と乖離があり, 実際はnon-stationary, つまり, $p_{a, t} = \mathbb{P} (a | x_t, \left(X_s, A_s R_s \right) )_{s=1}^{t-1}$ と定義するのが妥当です. この時, Biasについては本記事における分析がほとんどそのまま成り立ちますが, Varianceについては共分散項が大量に出てくるため分析が難しく, 元論文においてもstationaryの場合のみVarianceが導出されています. よって, Varianceについてはあくまで参考程度に留めておくのが良い態度と思いますが, 実験的にはDRやMRDRの性能が良いことが知られており, それがVarianceを抑えることができていることに起因すると考えられています.

(注2)
前半では, $\pi^{new}$についてもstationary policyつまり, $A_t \sim \pi \left( . | X_t \right)$としていましたが, 実験では, $\pi^{new}$の候補としてnon-stationary policyつまり, $A_t \sim \pi \left( . | X_t, \left(X_s, A_s, R_s \right)_{s=1}^{t-1} \right)$を用いましたが, DRやMRDRを用いて性能をうまく推定できました.

興味を持たれた方へ

因果推論やバンディット関連で過去に以下の記事を書きましたので, もう少し雰囲気を掴んでみたいと思われら是非！

参考

[1] L. Li, W. Chu, J. Langford, and X. Wang. Unbiased offline evaluation of contextual-bandit-based news article recommendation algorithms. In Proceedings of the Web Search and Data Mining (WSDM), pp. 297–306. ACM, 2011.

[2] M. Dudík, J. Langford, and L. Li. Doubly robust policy evaluation and learning. Proceedings of the 28th International Conference on Machine Learning, Bellevue, WA, USA, 2011.

[3] N. Jiang and L. Li. Doubly robust off-policy value evaluation for reinforcement learning. Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 2016. JMLR: W&CP volume 48.

[4] Y. X. Wang, A. Agarwal, and M. Dudik. Optimal and adaptive off-policy evaluation in contextual bandits. In International Conference on Machine Learning, 2017.

[5] M. Farajtabar, Y. Chow, and M. Ghavamzadeh. More robust doubly robust off-policy evaluation. In International Conference on Machine Learning, 2018.

[6] 本多淳也, 中村篤祥. バンディット問題の理論とアルゴリズム. 講談社機械学習プロフェッショナルシリーズ, 2016.

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up