はじめに
前回の基本編では、多腕バンディットアルゴリズムにおいて用いられる基本的なアルゴリズムを紹介し、簡単な実験をしてみました。今回は、それに引き続いてアームから得られる報酬の期待値パラメータをベイズ統計的な枠組みでモデル化するThompson Samplingについて紹介します。また、前回紹介したアルゴリズム群とThompson Samplingの性能を広告配信を模した2つの実験によって比較してみます。
今回の実験で使用したコード・ファイルはこちらからご覧にいただけます。
また、バンディットアルゴリズムについてまだよく知らない方は、前回の記事や他のQiitaの記事を先に見ておくと良いと思います。
目次
- Thompson Samplingとは
- ベルヌーイ分布に従う報酬の期待値の事後分布
- 実験1
- 実験2
- さいごに
- 参考
Thompson Samplingとは
前回紹介したUCB1アルゴリズムは頻度論の考え方に基づいて各アームから得られた報酬の標本平均の真の期待値からのズレをHoeffdingの不等式により評価することで信頼区間を構成し、その上側信頼区間が最大のアームを各試行で選んでいきました。このUCB1アルゴリズムはアームに対する既知情報が同じだった場合は全て同じアームを選択するという意味で決定的なアルゴリズムと言えるでしょう。このようなアルゴリズムは例えば広告配信などインプレッション毎というよりもバッチ的に推定量を更新するような状況において不安定な挙動を示す可能性があります。
一方で今回の主題であるThompson Samplingは各時点においてそれぞれのアームを「そのアームが期待値最大である確率」で選択します。つまり、既知情報が全く同じ状況でも異なるアームを引くことがあり、推定量のバッチ更新に対して頑健な性質を持ちます。(このような方法を確率一致法と呼びます。)
また、Thompson Samplingは確率一致法の中でもベイズ的な枠組みで報酬の事後分布をモデル化します。今回は一例として、アーム$i$の報酬$x_{i,t}$が真の期待値パラメータ$\mu_i$のベルヌーイ分布$Ber(x_i | \mu_i) \in [0,1]$に従うとして、事後分布を簡単に導いてみます。
以下、表のように記号を用います.
| 記号 | 意味 |
|---|---|
| $K$ | アームの集合 |
| $T$ | 総試行回数 |
| $t$ | (ある時点までの)試行回数 |
| $t_k$ | (ある時点までの)腕$k$の試行回数 |
| $a_t , (\in K)$ | $t$において選択するアーム (t-1回の試行による情報からアルゴリズムが決定) |
| $x_{ a_t, t}$ | t回目の試行で選択されるアーム $a_t$ から得られる報酬 |
| $X_{n_i}$ | 腕$i$を$n_i$回引いた時に観測された(累積の)報酬のベクトル 各試行$t$において報酬は独立に観測される. |
| $\mu_k$ | 各腕$k$から得られる報酬の真の期待値 |
| $\hat{\mu_k}$ | 腕$k$から得られる報酬の期待値の推定値 その時点までの腕$k$から得られた報酬の標本平均 |
ベルヌーイ分布に従う報酬の期待値の事後分布
先ほど報酬の分布についてベルヌーイ分布を仮定しました。ベルヌーイ分布の事前分布として今回は事後分布を解析的に計算できるようベータ分布$Beta(\alpha | \beta)$を用いることとします。アーム$i$を$n_k$回選択し、当たりが$m_k$回出たとすると報酬の真の期待値パラメータ$\mu_k$の事後分布は以下のように導出されます。
\begin{align}
p(\mu_k | X_{n_k}) & = \frac{p(X_{n_k} | \mu_k)p(\mu_k)}{p(X_{n_k})} \\
& \propto p(X_{n_k} | \mu_k)p(\mu_k) \\
& = \Bigl(\prod_{t=k}^{n_k}p(x_t | \mu_k) \Bigr)p(\mu_k)
\\ \\
\ln{p(\mu_k | X_{n_k})} & = \sum_{t=1}^{n_k}\ln{p(x_t | \mu_k)} + \ln{p(\mu_k)} + const. \\
& = \sum_{t=1}^{n_k}\ln{Ber(x_t | \mu_k)} + \ln{Beta(\alpha | \beta)} + const. \\
& = \sum_{t=1}^{n_k}x_t\ln{\mu_k} + \sum_{t=1}^{n_k}(1 - x_t)\ln{(1 - \mu_k)} \\ & + (\alpha - 1)\ln{\mu_k} + (\beta - 1)\ln{\mu_k} + const. \\
& = (m_k + \alpha - 1)\ln{\mu_k} + \{(n_k - m_k) + \beta - 1\}\ln(1 - \mu_k) + const. \\
& = Beta(m_k + \alpha | n_k - m_k+ \beta)
\end{align}
したがって、$n_k$回の試行で当たりが$m_k$回でたアーム$k$の報酬の期待値パラメータ$\mu_k$の事後分布は、事前分布のパラメータ$\alpha, \beta$にそれぞれ、当たりの数$m_k$とはずれの数$n_k - m_k$を加えた数を新たなパラメータとするベータ分布に従うことになります。そしてこの事後分布を全てのアームについて計算した後に以下のようにして$a_t$を決めるのがThompson Samplingになります。こうすることにより、$t$回目の試行においてそれぞれのアームを期待値最大である確率で選択できることが(近似的に)期待されます。
\begin{align}
& a_t = \arg\max_{k \in 1, ... ,K} \hat{\mu_k} \\
& \hat{\mu_k} \sim Beta(m_k + \alpha | n_k - m_k + \beta)
\end{align}
ちなみに、それぞれのアームが期待値最大となる確率は以下のような積分を計算しなければ算出できませんが、これは簡単には計算ができません。しかし、Thompson Samplingでは各々のアーム期待値が最大となる確率それ自体がわからなくてもその確率で各アームを選択できれば良いため上記のような方法で上手くいくことが多いです。こちらのp.27に詳しい解説があります。(これが確率一致法と呼ばれる所以なのかもしれません。)
p(\mu_k = \mu_k^*) = \int_0^1 p(x_k | X) \Bigl(\prod_{i \neq j} \int_0^{x_i}p(x_j | X)dx_j \Bigr)dx_i
Thompson Samplingのアルゴリズムについて説明が終わったところでいよいよ実験パートに入っていきます。
余談
今回は先に述べたようにUCB1とThompson Samplingの性能を比較してThompson Samplingがどのような場合に優れているのかを調べたいと思っていたのですが、UCB1が思ったよりも弱くて比較になりませんでした。そこで、UCB1の提案論文[3]からUCB_tunedというアルゴリズムを持ってきて実装し、Thompson Samplingとの比較に用いることにしました。UCB_tunedは各試行において以下の式により選択するアームを決定します。しかし、UCB_tunedは経験的にUCB1よりも性能が良いらしいのですが、理論的性質については示すことが出来なかったと論文にも書かれていました。($\hat{\sigma_k}$は腕$k$の標本分散となっています.)
\begin{align}
a_t = \arg\max_{k \in 1, ... ,K} \hat{\mu_k} + \sqrt{\frac{\log{t_k}}{T} min\{ \frac{1}{4} \, , \hat{\sigma_k} + \sqrt{ \frac{2 \log{t_k}}{T}} \}}
\end{align}
実験1
シミュレーション1ではトータルで10,000回広告を打つチャンスがある中でクリック数を最大化する性能を評価します。広告の種類は10種類とし、それぞれが以下のような期待値パラメータを持つベルヌーイ分布に従ってクリックの有無を報酬として出力するようなケースを考えます。広告の期待値は平均0.05、分散0.04の正規分布からランダムに10個サンプルしました。 (ただし、0.005以上0.2以下の範囲に収まるようにしました。)
| 広告の種類 | 広告1 | 広告2|広告3|広告4|広告5|広告6|広告7|広告8|広告9|広告10|
|-----------|------------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|
| 期待値$\mu_i$|0.053|0.065|0.09|0.066|0.066|0.103|0.029|0.097|0.099|0.04|
実験1では以下のアルゴリズムの性能を比較します。
| アルゴリズム | ハイパーパラメータ |
|---|---|
| ε-greedy | $\epsilon = 0.01$ |
| ε-greedy | $\epsilon = 0.05$ |
| UCB1 | なし |
| UCB_tuned | なし |
| Thompson Sampling | なし($\alpha=\beta=1$) |
それでは、以下にシミュレーションの結果を描画します。描画における値は100回のシミュレーションの平均値を用いています。
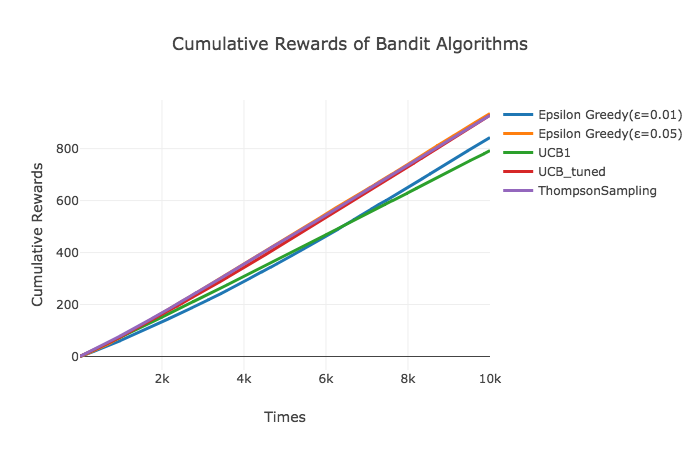
こちらは、10,000回の試行でどれだけクリックを稼ぐことができたかを表しています。最も良い性能を示したThompson SamplingやUCB_tunedは、期待値が最も良かった広告でも0.103だったにも関わらず、10,000回の試行で900程度のクリックを稼いだようです。意外だったのは比較的性能が良いことで知られているUCB1がε-greedyに大きな差で敗れていたことです。これはUCB1のアーム選択に用いられている式が導かれるにあたって用いられている確率不等式に関係していそう*です。
余談
UCB1のアーム選択に用いられる式はHoeffdingの不等式に基づいているのですが、これは真の期待値と標本平均の誤差が起こり得る確率の上界を与えているに過ぎず、分布によってはその確率を過大評価してしまいます。例えば、正規分布やsub-gaussianと呼ばれる性質を持つ分布に対しては精度よく誤差を評価できるのですが、ベルヌーイ分布(特に$\mu$が0.5から大きく離れている場合)はHoeffdingの不等式では良い評価をすることができないことが知られています。これは、Hoeffdingの不等式が分布に対する仮定をおいていないことに起因しており、分布の仮定をおいた場合は、Chernoff-Hoeffdingの不等式として知られるさらに精度の良い誤差評価の不等式が存在します。この不等式に基づいたバンディットアルゴリズムとしてKL-UCBというものが存在し、ベルヌーイ分布に対しても性能を発揮できるようにそのアルゴリズムが構成されています。
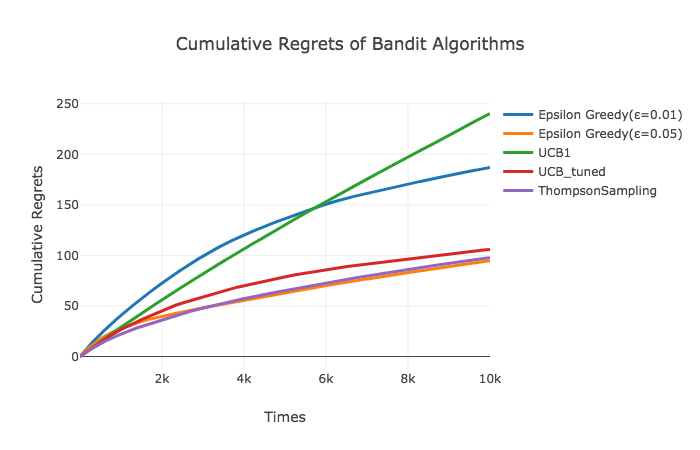
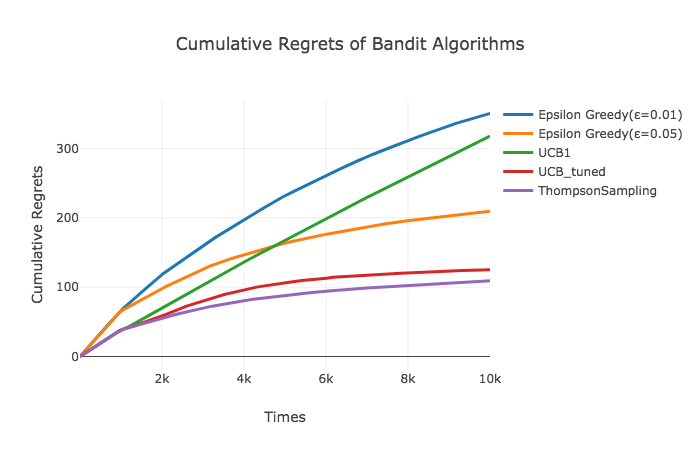
以下の描画は累積リグレット(最大の期待値と選択した広告の期待値の差の合計)を表しています。Thompson SamplingやUCB_tunedは2,000回を超えたあたりからリグレットの増分が減少し始めていますが、UCB1はもうしばらく試行を続けてもリグレットが増え続けるように見えます。
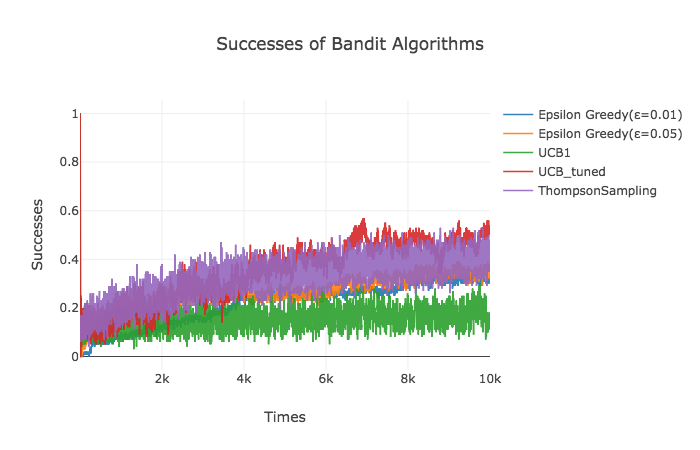
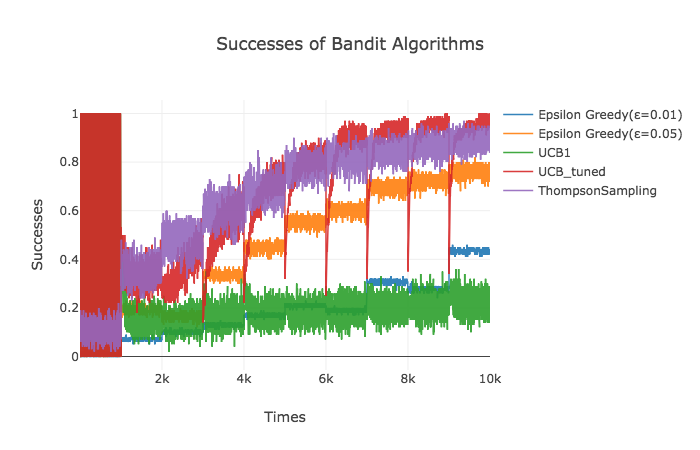
次にアルゴリズム が各試行回数においてどれだけの割合で最も期待値が高い広告を選択したのかを見てみます。今回は、広告3,6,8,9の期待値が似通っているという非常に難しい設定になってしまったこともあり、Thompson SamplingやUCB_tunedでも10,000回の試行を終えたあたりで約40%ほどしか最も期待値の高かった広告を選べていませんでした。
それぞれのアルゴリズムが10種類の広告をどれくらいの割合で選んだのかも見てみましょう。Thompson SamplingとUCB_tunedは全体を通じて約35%の確率で最適な広告6を選んでいました。また、期待値が0.09以上だった広告3,8,9を含めると両者85%程の試行をこれら4つの広告に対して費やしています。
| 広告の種類
(真の期待値) | 広告1
(0.053)|広告2
(0.065)|広告3
(0.090)|広告4
(0.066)|広告5
(0.066)|広告6
(0.103)|広告7
(0.029)|広告8
(0.097)|広告9
(0.099)|広告10
(0.040)|
|-----------|------------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|
|ε-greedy
($\epsilon = 0.01$)|23.7%|2.9%|9.8%|2.4%|4.6%|21.6%|0.1%|14.9%|19.8%|0.2%|
|ε-greedy
($\epsilon = 0.05$)|4.6%|1.0%|18.7%|1.8%|1.7%|26.5%|0.6%|24.3%|20.3%|0.7%|
|UCB1|7.2%|8.4%|12.4%|8.4%|8.5%|15.2%|5.5%|13.8%|14.4%|6.2%|
|UCB_tuned|2.6%|3.2%|10.3%|3.2%|3.3%|35.0%|1.7%|15.1%|23.6%|1.9%|
|Thompson Sampling|2.0%|3.1%|12.1%|3.0%|3.5%|32.3%|1.1%|19.0%|22.7%|1.3%|
実験2
さて実験2でもトータルで10,000回広告を打つチャンスがある中でクリック数を最大化する性能を評価するのですが、各広告を打った後の報酬の情報は逐一得られるわけではなく1,000個ごとに得られるバッチ更新の場合を仮定します。広告の種類は実験2でも平均0.05、分散0.04の正規分布からサンプルした以下の10種類の広告を用いることにしました。(ただし、0.005以上0.2以下の範囲に収まるようにしました。)
| 広告の種類 | 広告1 | 広告2|広告3|広告4|広告5|広告6|広告7|広告8|広告9|広告10|
|-----------|------------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|
| 期待値$\mu_i$|0.008|0.017|0.052|0.005|0.037|0.075|0.044|0.044|0.058|0.035|
また、実験2では実験1と同様に以下のアルゴリズムの性能を比較します。
| アルゴリズム | ハイパーパラメータ |
|---|---|
| ε-greedy | $\epsilon = 0.01$ |
| ε-greedy | $\epsilon = 0.05$ |
| UCB1 | なし |
| UCB_tuned | なし |
| Thompson Sampling | なし($\alpha=\beta=1$) |
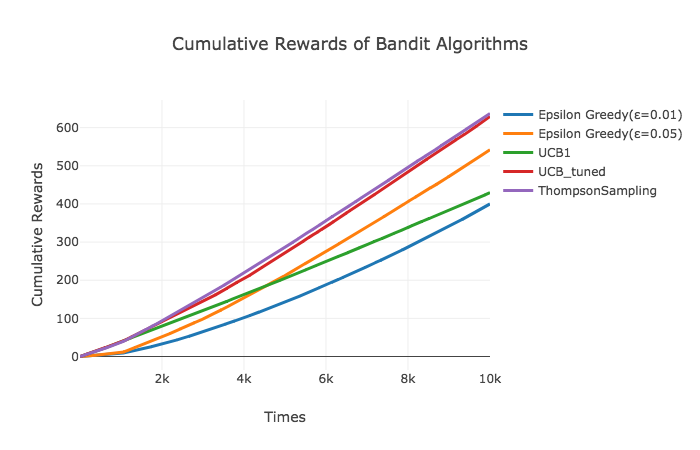
それでは、先ほどと同様に実験2の結果を描画します。各描画は100回のシミュレーションの平均値となっています。今回はThompson SamplingとがUCB_tunedよりも優れているように見えますが累積報酬は有意差がないように見えます。一方で累積リグレットを見るとThompson SamplingがUCB_tunedをある程度の差をつけて上回っています。やはりThompson Samplingはバッチ更新に対して比較的頑健なようです。
次にアルゴリズムが各試行回数においてどれだけの割合で最も期待値が高い広告を選択したのかを見てみます。最初の1,000回は広告に対する情報が何もないため、UCB系列のアルゴリズムは同じ広告を(argmaxで)選択し続けるためこのように混沌としています。ただし、どのアルゴリズムを見てみても、2,000回以降は広告に対する情報を更新するにつれて期待値が最大である広告6を選択する割合が(階段状に)増えていっています。最終的にThompson SamplingやUCB_tunedは90%以上の確率で広告6を選んでいます。
こちらの表を見てみると推定量がバッチ更新だったこともあり他のアルゴリズムは広告6をそれほど多く選べていないにも関わらず、UCB_tunedとThompson Samplingはしっかり全体の65%程度広告6を選べています。一方で、単純なUCB1アルゴリズムはかなり非効率な広告も一定程度選んでしまっており、バッチ更新に苦しんだ様子が伺えます。
余談
また、描画の左の方にUCBによって作られた赤い柱のような部分が存在しますが、これは情報を全く得られない最初の1,000回においては広告1~10までを順番に選択するよう実装したためです。こうすると、正解が10回に1回(今回の場合は広告6を10回に1回選択)選択することになり、正解を選択するのは全てシミュレーションで同じタイミングとなります。従って正解率は10回に1回1.0が10回に9回0.0がプロットされるのでそれを線で結ぶと上の描画における柱が現れるということになります。
| 広告の種類
(真の期待値) | 広告1
(0.008)|広告2
(0.017)|広告3
(0.052)|広告4
(0.005)|広告5
(0.037)|広告6
(0.075)|広告7
(0.044)|広告8
(0.035)|広告9
(0.058)|広告10
(0.035)|
|-----------|------------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|-----------|
|ε-greedy
($\epsilon = 0.01$)|29.5%|1.4%|12.2%|0.3%|6.4%|18.9%|6.7%|5.9%|12.6%|0.6%|
|ε-greedy
($\epsilon = 0.05$)|11.9%|2.5%|10.8%|0.9%|4.7%|45.1%|5.4%|4.0%|11.1%|3.6%|
|UCB1|6.4%|7.2%|11.6%|6.3%|9.4%|17.6%|10.5%|9.1%|12.9%|9.1%|
|UCB_tuned|2.0%|2.2%|6.6%|1.9%|3.5%|62.9%|4.5%|3.3%|9.6%|3.4%|
|Thompson Sampling|1.2%|1.4%|7.1%|1.1%|3.0%|64.2%|4.5%|2.9%|11.5%|3.0%|
さいごに
今回はQiitaであまり記事として取り上げられていなかったこともあり、Thompson Samplingを扱ってみました。次回は、バンディット問題の拡張である文脈付きバンディット問題を扱う予定です。
参考
[1] 本多淳也, 中村篤祥. バンディット問題の理論とアルゴリズム. 講談社 機械学習プロフェッショナルシリーズ.
[2] 須山敦志, 杉山将. ベイズ推論による機械学習入門. 講談社 機械学習スタートアップシリーズ.
[3] Auer, P., Cesa-bianchi, N. and Fischer, P. Finite-time Analysis of the Multiarmed Bandit Problem, Machine Learning, 2002.